Unit - 5
Complex Variable - Integration
Contour integration is the process of calculating the values of a contour integral around a given contour in the complex plane.
Example: Solve 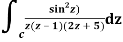 where
where 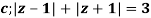
Answer
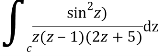
Where 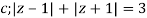
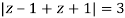
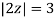
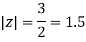
Poles of the inter are given by putting the denominator equal to zero.
Z(z-1)(2z+5)=0
Z=0,1,-5/2
The integrand has three simple poles at
Z=0,1,-5/2
The given circle |z|=3/2 with centre at z=0 and radius =3/2 encloses two poles z=0 and 1
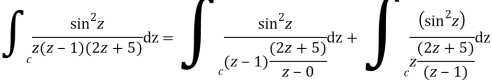
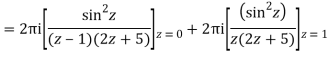

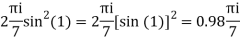
Example: Solve 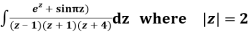
Answer
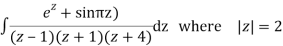
Poles are
|z-0|=2
Poles 1 and -1 inside the circle
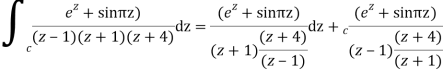
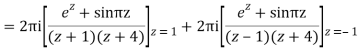
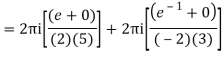
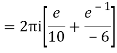
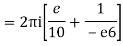
Derivation of Cauchy Integral theorem:
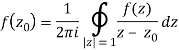
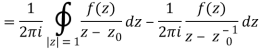
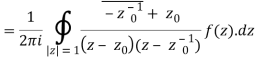
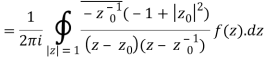
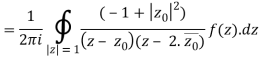
Example 1:
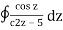 where C = | z – 3| = 2
where C = | z – 3| = 2
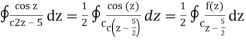 where f(z) = cosz
where f(z) = cosz
= ½ (2 πi) f(5/2) by cauchy’s integral formula
= πi. Cos (5/2)
Example 2:
Solve the following by cauchy’s integral method:
f(n)(a) = n!/2πi 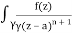
Solution:
Given,
f(n)(a) = n!/2πi 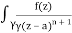
f(k + 1)(a) = d/da f(k)(a)
= k!/2πi 
= k!/2πi 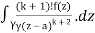
= (k+1)!/2πi 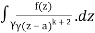
Cauchy’s integral formula-
Cauchy’s integral formula can be defined as-
f(a) = 1/2πi 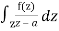
Where f(z) is analytic function within and on closed curve C, a is any point within C.
Example-1: Evaluate 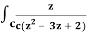 dz by using Cauchy’s integral formula.
dz by using Cauchy’s integral formula.
Here c is the circle |z - 2| = 1/2
Sol. It is given that-
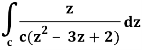
Find its poles by equating denominator equals to zero.
z2 – 3z + 2 = 0
(z – 1)(z – 2) = 0
z = 1, 2
There is one pole inside the circle, z = 2,
So that-
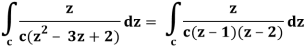
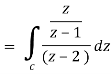
Now by using Cauchy’s integral formula, we get-
= 2πi [ z / z-1]z = 2 = 2πi(2/2 -1) = 4πi
Example-2: Evaluate the integral given below by using Cauchy’s integral formula-

Sol. Here we have-
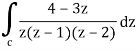
Find its poles by equating denominator equals to zero.
z(z – 1)(z – 2) = 0
We get-
z = 0,1, 2
There are two poles in the circle-
Z = 0 and z = 1
So that-
 = 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2πi . 4/(-1)(-2) + 2πi (4 -3)/1(1 -2) = 2πi(2 – 1) = 2πi
Example-3: Evaluate 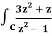 dz if c is circle |z - 1| = 1.
dz if c is circle |z - 1| = 1.
Sol. Here we have-
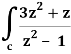
Find its poles by equating denominator equals to zero.
z2 – 1 = 0 or z2 = 1 or z = ± 1
The given circle encloses a simple pole at z = 1.
So that-
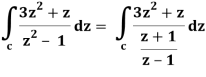 = 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 4πi
The value of z is said to be zero of the analytic function f(z) when f(z) = 0.
If f(z) is analytic in the neighbourhood of z = a, then by Taylor’s theorem-
f(z) = a0 + a1(z – a) + a2(z – a)2 + a3(z – a)3 + . . . + an(z – a)n+ . . .
If a0 = a1 = a2 = . . . = an – 1 = 0 but an is non- zero, then f(z) is said to have a zero of order n at z = a.
The zero is said to be simple if n = 1.
an = fn(a)/n!
For a zero of order m at z = a,
f(a) = f’(a) = f”(a) = fn – 1(a) = 0 but fn(a) ≠ 0
Thus in the neighbourhood of the zero at z = a of order n
f(z) = an(z – a)n + an+1 (z – a)n + 1 = (z – a)n [ an + an+1(z –a) + …] = (z – a)n ∅(z)
Where ∅(z) = an + an+1 (z – a) + . . . Is analytic and non-zero at and in the neighbourhood of z = a.
Example: Find out the zero of the following-
f(z) = (z – 2)/z2 sin 1/(z – 1)
Sol. Zeroes of the function-
f(z) = 0
(z – 2)/z2 sin 1/(z – 1) = 0
(z – 2)/z2 = 0, sin 1/(z – 1) = 0
z = 2, 1/(z – 1) = nπ ( n = 0, ±1, ±2 ….)
z = 2, 1 + 1/nπ (n = 0, ±1, ±2 ….)
Key takeaways-
- The pole is said to be simple pole when m = 1.
- Cauchy’s residue theorem-
If f(z) is analytic in a closed curve C, except at a finite number of poles within C, then-
z = [ cos 5π/4 + i sin 5π/4] = ( - 1/2 – i 1/2)
A point at which a function f(z) is not analytic is known as a singular point or singularity of the function.
Isolated singular point- If z = a is a singularity of f(z) and if there is no other singularity within a small circle surrounding the point z = a, then z = a is said to be an isolated singularity of the function f (z); otherwise it is called non-isolated.
Pole of order m- Suppose a function f(z) have an isolated singular point z = a, f(z) can be expanded in a Laurent’s series around z = a, giving
= 2πi [ (4 – 3z)/(z – 1)(z – 2)]z = 0 + 2πi [(4 – 3z)/z(z -2)]z = 1
= 2πi. 4/(-1)(-2) + 2πi . (4 – 3)/1(1 – 2) = 2πi(2 – 1) = 2πi …….(1)
In some cases it may happen that the coefficient bm + 1 = bm + 2 = bm + 3 = 0 , then equation (1) becomes-
= 2πi[(3z2+z)/(z+1)]z = 1 = 2πi(3+1)/(1+1)
f(z) = a0 + a1(z – a) + a2(z – a)2 + . . . + b1/(z – a) + b2/(z – a)2 + . . .+ bm/(z – a)m+ bm+1/(z – a)m +1 + bm+2/(z – a)m+2 + . . .
Then z = a is said to be a pole of order m of the function f(z).
Note- The pole is said to be simple pole when m = 1.
In this case-
f(z) = a0 + a1(z – a) + a2(z – a)2 + . . . + b1/(z – a) + b2/(z – a)2 + . . .+ bm/(z – a)m
Working steps to find singularity-
Step-1: If 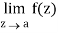 exists and it is finite then z = a is a removable singular point.
exists and it is finite then z = a is a removable singular point.
Step-2: If 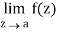 does not exists then z = a is an essential singular point.
does not exists then z = a is an essential singular point.
Step-3: If 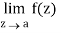 is infinite then f(z) has a pole at z = a. The order of the pole is same as the number of negative power terms in the series expansion of f(z).
is infinite then f(z) has a pole at z = a. The order of the pole is same as the number of negative power terms in the series expansion of f(z).
Example: Find the singularity of the function-
f(z) = sin 1/z
Sol.
As we know that-f(z) = a0 +a1(z – a) + a2(z – a)2 + . . . + 1/(z – a)m[ b1(z – a)m – 1 + b2(z – a)m – 2 + b3(z – a)m – 3 + . . . + bm}
So that there is a number of singularity.
Sin 1/z is not analytic at z = a
(1/z = ∞ at z = 0)
Example: Find the singularity of 1/(1 – ez) at z = 2πi
Sol.
Here we have-
f(z) = 1/(1 – ez)
We find the poles by putting the denominator equals to zero.
That means-
1 – ez = 0
ez = 0 = ( cos 2n π + i sin 2n π) = e2nπi
z = 2nπi(n = 0, ±1, ±2, ….)
z = 2n π i is a simple pole
Example: Determine the poles of the function-
f(z) = 1/(z4 +1)
Sol.
Here we have-
f(z) = 1/(z4+1)
We find the poles by putting the denominator of the function equals to zero-
We get-
z4 + 1 = 0 and z4 = - 1
f(z) = a0 + a1(z – a) + a2(z – a)2 + . . . + b1/z - a
By De Moivre’s theorem-
Sin 1/z = 1/z – 1/3!z3 + 1/5!z5 + . ….+ (-1)n 1/(2n+1)! z2n+1
z = (-1)1/4 = (cos π + i sin π)1/4
If n = 0, then pole-
= [ cos (2n + 1)π + i sin (2n + 1)π]1/4
If n = 1, then pole-
= [ cos (2n + 1)π/4 + i sin (2n+1)π/4]
If n = 2, then pole-
z = [ cos π/4 + i sin π/4] = (1/2 + i 1/2)
If n = 3, then pole-
z = [ cos 3π/4 + i sin 3π/4] = (- 1/2 + i 1/2)
Let 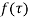 be analytic at all points within a circle
be analytic at all points within a circle 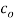 with centre
with centre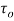 and radius
and radius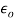 . Then
. Then
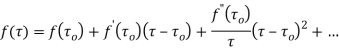
Example: Expand the function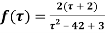
In a Taylor's series about the point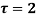
Ans. Using partial fraction method
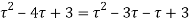

(τ-1)(τ-3)
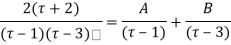
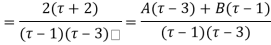

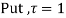
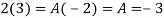
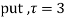
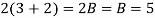

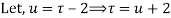
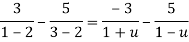
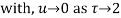
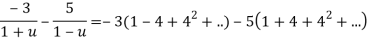
Both series converge when |4|<1
Therefore 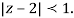 The series converges in the circle centred at
The series converges in the circle centred at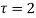 with radius of 1.
with radius of 1.
Taylor’s series expansion is
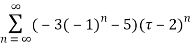
Example: Show that when 0<|z|<4
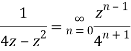
Solution When |z|<4 we have
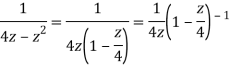
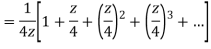
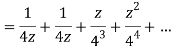
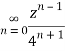
Example: Expand 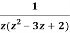 for the regions
for the regions
- 0<|z|<1
- 1<|z|<2
- |z|>2
Solution Let 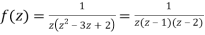
Hence resolving into partial functions we get

1) For 0<|z|<1 we have
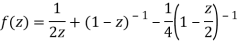
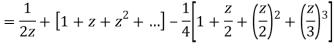
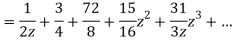
2) For 1<|z|<2 we have

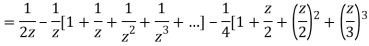
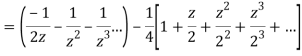
3) For |z|>2 we have
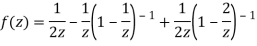
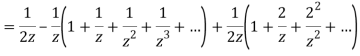
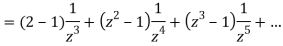
Let 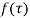 be analytic in the ring shaped region D bounded by two concentric circles
be analytic in the ring shaped region D bounded by two concentric circles 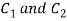 with centre
with centre 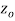 and radii
and radii 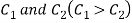 and let be any point of D. Then
and let be any point of D. Then
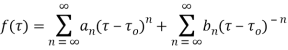
Example: using Taylor's series
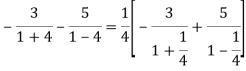

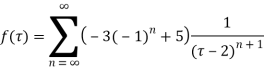
Example: Obtain the Taylor’s and Laurent’s series which represents the function 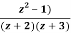 in the regions
in the regions
1) |z|<2
2) 2<|z|<3
3) |z|>3
Solution We have
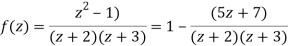
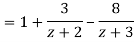
1) For |z|<2 we have
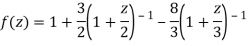
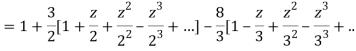
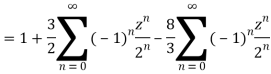

Which is Taylor’s series valid for |z|<2
2) For 2<|z|<3 we have
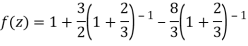
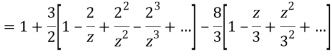

3) For |z|<3
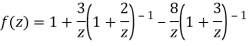
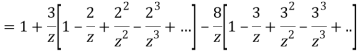
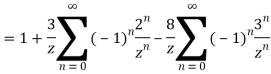
Let be a pole of order m of a function
be a pole of order m of a function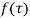 and
and 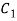 circle of radius r with centre at
circle of radius r with centre at 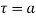 which does not contain any other singularities except at
which does not contain any other singularities except at then
then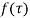 is analytic within the
is analytic within the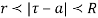 can be expanded by Laurent’s series
can be expanded by Laurent’s series
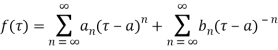
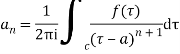
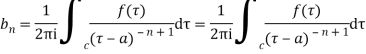
The coefficient of  is called residue of
is called residue of 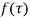 at the pole then
at the pole then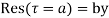
Method of finding residue
(1) If 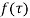 has a simple pole at
has a simple pole at 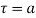 then
then 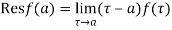
(2) If is of the form
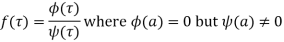
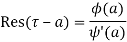
(3) If 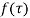 has a pole of order n at
has a pole of order n at 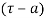 then
then
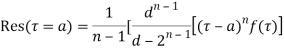
(4) Residue at a pole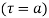 of any order
of any order
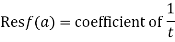
(5) Residue of  at
at 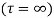
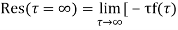
Example: Find residue of the function

Answer
Let 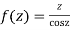
The singularities of f(z) are given by 
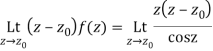
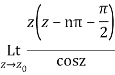
Which is of the form 
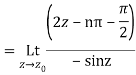
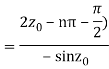
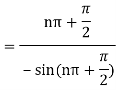
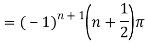
Example: Find the residue of 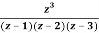 at z=1
at z=1
Answer
Let f(z)=
The poles of f(z) are determined by putting the denominator equal to zero
(z-1)(z-2)(z-3)=0
Z=1,2,3
Residue of f(z) at z=1=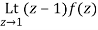
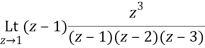
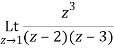
=1/2
Example: Find the residue of 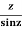
Answer
f(z)=
Poles are determined by putting sinz=0=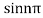
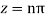
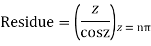
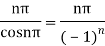
Hence the residue of the given function at pole 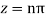 is
is 
If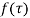 is analytic in a closed curve c except at a finite number of poles within c then
is analytic in a closed curve c except at a finite number of poles within c then
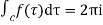 [Sum of residue at the pole within c]
[Sum of residue at the pole within c]
Example: Evaluate the following integral using residue theorem
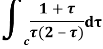
Where c is the circle.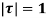 .
.
Ans.
The poles of the integral are given by putting the denominator equal to zero

The integral is analytic on  and all points inside except
and all points inside except as a pole at
as a pole at 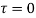 is inside the circle
is inside the circle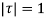
Hence by residue theorem

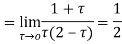
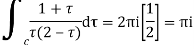
Example: Evaluate 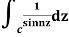 where c;|z|=4
where c;|z|=4
Answer
Here f(z)=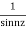
Poles are 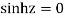
Sin iz=0
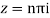
Poles 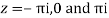
Lie inside the circle |z|=4
The given function 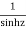 is of the form
is of the form 
Its pole at z=a is 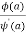
Residue (at 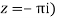
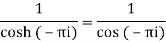
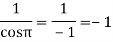
Residue at z=0=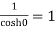
Residue at  =
=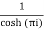
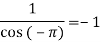
Residue at 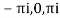 are
are
Respectively -1,1 and -1
Hence the required integrand
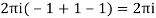
Example: Evaluate 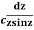 :c is the unit circle about the origin
:c is the unit circle about the origin
Answer
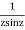 =
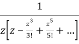
=
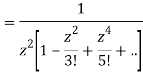
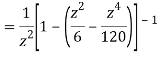
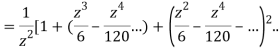

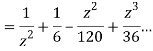
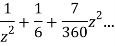
This shows that z=0 is a pole of order 2 for the function  and the residue of the poles is zero(coefficient of 1/z)
and the residue of the poles is zero(coefficient of 1/z)
Now the pole at z=0 lies within c
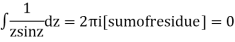
Example: Evaluation of definite integral
Show that 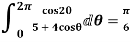
Solution
I= 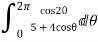
Real part of 
Now I= 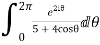 =
=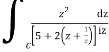
Putting z=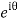 where c is the unit circle |z|=1
where c is the unit circle |z|=1
I=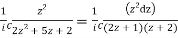
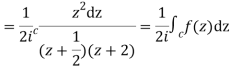
Now f(z) has simple poles at 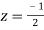 and z=-2 of which only
and z=-2 of which only  lies inside c.
lies inside c.
Residue at 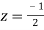 is
is 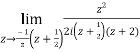
=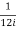
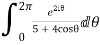 =
=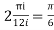
Now equating real parts on both sides we get
I=
Example: Prove that 
Solution
Let 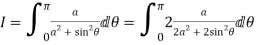

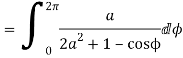
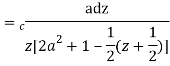
Putting 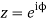 where c is the unit circle |z|=1
where c is the unit circle |z|=1
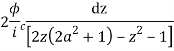
2ai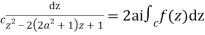
Poles of f(z) are given by the roots of
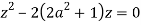
Or 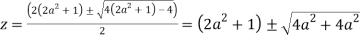
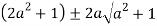
Let 
Clearly  and since
and since 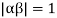 we have
we have 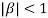 Hence the only pole inside c is at z=
Hence the only pole inside c is at z=
Residue (at  )
)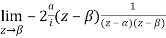
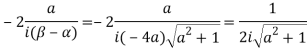
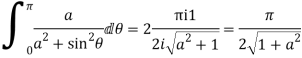

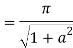
Example: Evaluate 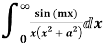
Answer
Consider 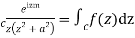
Where c is the closed contour consisting of
1) Real axis from 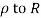
2) Large semicircle in the upper half plane given by |z|=R
3) The real axis -R to 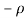 and
and
4) Small semicircle given by |z|=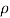
Now f(z) has simple poles at z=0 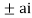 of which only z=
of which only z=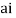 is avoided by indentation
is avoided by indentation
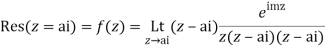
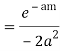
Hence by Cauchy’s Residue theorem
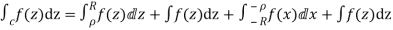
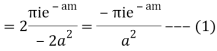
Since 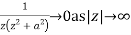 and
and
Hence by Jordan’s Lemma 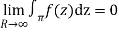
Also since 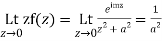
Hence 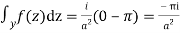
Hence as 

Equating imaginary parts we get

Example: Prove that 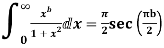
Solution
Consider 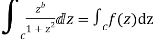
Where c is the contour consisting of a large semicircle in the upper half plane indented at the origin as shown in the figure
Here we have avoided the branch point o, of 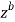 by indenting the origin
by indenting the origin
Then only simple of f(z) within c is at z=i
The residue(at z=i) =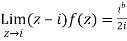
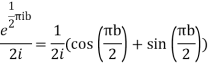
Hence by residue theorem
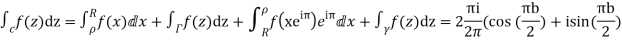
Since 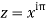 on -ve real axis.
on -ve real axis.
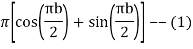
Now 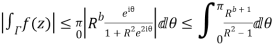
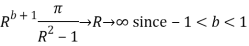
Similarly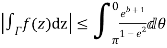
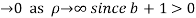
Hence when 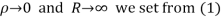
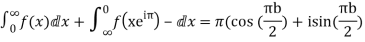
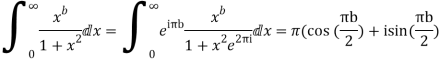
Equating real parts we get
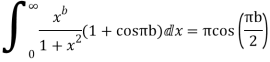
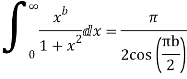
Fourier Integral: Improper Integral Involving Trigonometric Functions
The integrals
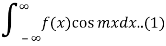
Can be evaluated by integrating
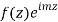
By residue theorem

Where the summation extends to all poles of 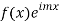 in the upper half=plane (since |
in the upper half=plane (since |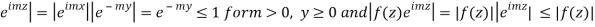 it follows that
it follows that
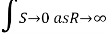
Equating the real and imaginary
Parts of (3), we get
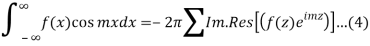
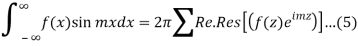
Example: Evaluate-
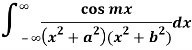
Sol:
We know that 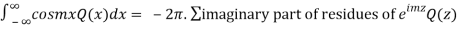 atits poles in the upper half plane. So consider
atits poles in the upper half plane. So consider
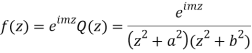
(z) has simple poles at z = ±ai, z = ±bi out of which z = ai, bi lies in the upper half plane.
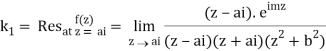
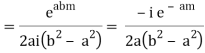
Similarly,


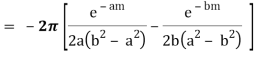
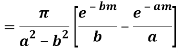
Example: Evaluate:
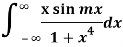
Sol:
We know that  atits poles in the upper half plane.
atits poles in the upper half plane.
So consider 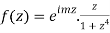 which has singular points at z =
which has singular points at z = 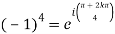 for k = 0, 1, 2, 3. Out of these four, only
for k = 0, 1, 2, 3. Out of these four, only 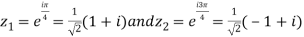 lies in the
lies in the
Upper half plane.

Which is 0/0 form, Applying L’ Hostpital’s rule

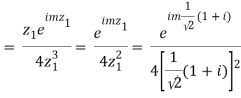
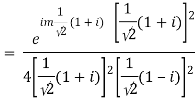
Real part of k1 = ¼ e-m/2 . Sin m/2
Similarly
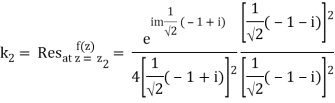

Real part of k2 = ¼ e- m/2 . Sin m/2
Then
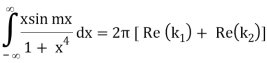
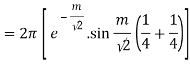
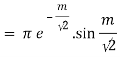
References:
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
Unit - 5
Complex Variable - Integration
Contour integration is the process of calculating the values of a contour integral around a given contour in the complex plane.
Example: Solve 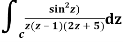 where
where 
Answer
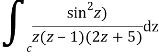
Where 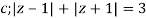
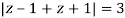

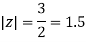
Poles of the inter are given by putting the denominator equal to zero.
Z(z-1)(2z+5)=0
Z=0,1,-5/2
The integrand has three simple poles at
Z=0,1,-5/2
The given circle |z|=3/2 with centre at z=0 and radius =3/2 encloses two poles z=0 and 1
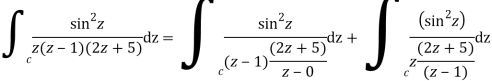
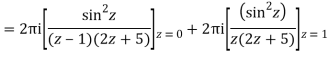
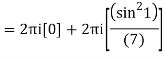
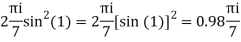
Example: Solve 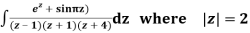
Answer
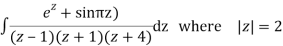
Poles are
|z-0|=2
Poles 1 and -1 inside the circle
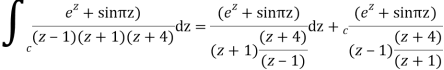
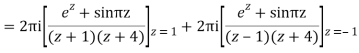
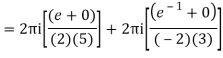
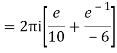
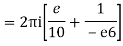
Derivation of Cauchy Integral theorem:
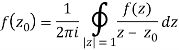
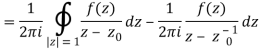
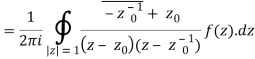
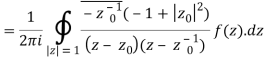
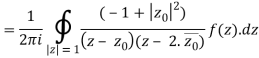
Example 1:
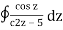 where C = | z – 3| = 2
where C = | z – 3| = 2
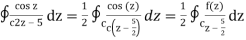 where f(z) = cosz
where f(z) = cosz
= ½ (2 πi) f(5/2) by cauchy’s integral formula
= πi. Cos (5/2)
Example 2:
Solve the following by cauchy’s integral method:
f(n)(a) = n!/2πi 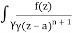
Solution:
Given,
f(n)(a) = n!/2πi 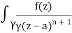
f(k + 1)(a) = d/da f(k)(a)
= k!/2πi 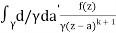
= k!/2πi 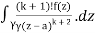
= (k+1)!/2πi 
Cauchy’s integral formula-
Cauchy’s integral formula can be defined as-
f(a) = 1/2πi 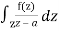
Where f(z) is analytic function within and on closed curve C, a is any point within C.
Example-1: Evaluate 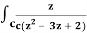 dz by using Cauchy’s integral formula.
dz by using Cauchy’s integral formula.
Here c is the circle |z - 2| = 1/2
Sol. It is given that-
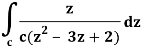
Find its poles by equating denominator equals to zero.
z2 – 3z + 2 = 0
(z – 1)(z – 2) = 0
z = 1, 2
There is one pole inside the circle, z = 2,
So that-
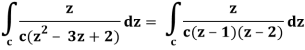
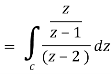
Now by using Cauchy’s integral formula, we get-
= 2πi [ z / z-1]z = 2 = 2πi(2/2 -1) = 4πi
Example-2: Evaluate the integral given below by using Cauchy’s integral formula-

Sol. Here we have-
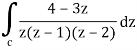
Find its poles by equating denominator equals to zero.
z(z – 1)(z – 2) = 0
We get-
z = 0,1, 2
There are two poles in the circle-
Z = 0 and z = 1
So that-
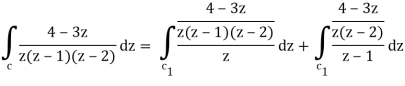 = 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2πi . 4/(-1)(-2) + 2πi (4 -3)/1(1 -2) = 2πi(2 – 1) = 2πi
Example-3: Evaluate 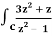 dz if c is circle |z - 1| = 1.
dz if c is circle |z - 1| = 1.
Sol. Here we have-
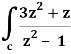
Find its poles by equating denominator equals to zero.
z2 – 1 = 0 or z2 = 1 or z = ± 1
The given circle encloses a simple pole at z = 1.
So that-
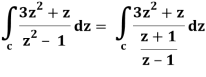 = 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 4πi
The value of z is said to be zero of the analytic function f(z) when f(z) = 0.
If f(z) is analytic in the neighbourhood of z = a, then by Taylor’s theorem-
f(z) = a0 + a1(z – a) + a2(z – a)2 + a3(z – a)3 + . . . + an(z – a)n+ . . .
If a0 = a1 = a2 = . . . = an – 1 = 0 but an is non- zero, then f(z) is said to have a zero of order n at z = a.
The zero is said to be simple if n = 1.
an = fn(a)/n!
For a zero of order m at z = a,
f(a) = f’(a) = f”(a) = fn – 1(a) = 0 but fn(a) ≠ 0
Thus in the neighbourhood of the zero at z = a of order n
f(z) = an(z – a)n + an+1 (z – a)n + 1 = (z – a)n [ an + an+1(z –a) + …] = (z – a)n ∅(z)
Where ∅(z) = an + an+1 (z – a) + . . . Is analytic and non-zero at and in the neighbourhood of z = a.
Example: Find out the zero of the following-
f(z) = (z – 2)/z2 sin 1/(z – 1)
Sol. Zeroes of the function-
f(z) = 0
(z – 2)/z2 sin 1/(z – 1) = 0
(z – 2)/z2 = 0, sin 1/(z – 1) = 0
z = 2, 1/(z – 1) = nπ ( n = 0, ±1, ±2 ….)
z = 2, 1 + 1/nπ (n = 0, ±1, ±2 ….)
Key takeaways-
- The pole is said to be simple pole when m = 1.
- Cauchy’s residue theorem-
If f(z) is analytic in a closed curve C, except at a finite number of poles within C, then-
z = [ cos 5π/4 + i sin 5π/4] = ( - 1/2 – i 1/2)
A point at which a function f(z) is not analytic is known as a singular point or singularity of the function.
Isolated singular point- If z = a is a singularity of f(z) and if there is no other singularity within a small circle surrounding the point z = a, then z = a is said to be an isolated singularity of the function f (z); otherwise it is called non-isolated.
Pole of order m- Suppose a function f(z) have an isolated singular point z = a, f(z) can be expanded in a Laurent’s series around z = a, giving
= 2πi [ (4 – 3z)/(z – 1)(z – 2)]z = 0 + 2πi [(4 – 3z)/z(z -2)]z = 1
= 2πi. 4/(-1)(-2) + 2πi . (4 – 3)/1(1 – 2) = 2πi(2 – 1) = 2πi …….(1)
In some cases it may happen that the coefficient bm + 1 = bm + 2 = bm + 3 = 0 , then equation (1) becomes-
= 2πi[(3z2+z)/(z+1)]z = 1 = 2πi(3+1)/(1+1)
f(z) = a0 + a1(z – a) + a2(z – a)2 + . . . + b1/(z – a) + b2/(z – a)2 + . . .+ bm/(z – a)m+ bm+1/(z – a)m +1 + bm+2/(z – a)m+2 + . . .
Then z = a is said to be a pole of order m of the function f(z).
Note- The pole is said to be simple pole when m = 1.
In this case-
f(z) = a0 + a1(z – a) + a2(z – a)2 + . . . + b1/(z – a) + b2/(z – a)2 + . . .+ bm/(z – a)m
Working steps to find singularity-
Step-1: If 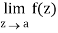 exists and it is finite then z = a is a removable singular point.
exists and it is finite then z = a is a removable singular point.
Step-2: If 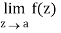 does not exists then z = a is an essential singular point.
does not exists then z = a is an essential singular point.
Step-3: If  is infinite then f(z) has a pole at z = a. The order of the pole is same as the number of negative power terms in the series expansion of f(z).
is infinite then f(z) has a pole at z = a. The order of the pole is same as the number of negative power terms in the series expansion of f(z).
Example: Find the singularity of the function-
f(z) = sin 1/z
Sol.
As we know that-f(z) = a0 +a1(z – a) + a2(z – a)2 + . . . + 1/(z – a)m[ b1(z – a)m – 1 + b2(z – a)m – 2 + b3(z – a)m – 3 + . . . + bm}
So that there is a number of singularity.
Sin 1/z is not analytic at z = a
(1/z = ∞ at z = 0)
Example: Find the singularity of 1/(1 – ez) at z = 2πi
Sol.
Here we have-
f(z) = 1/(1 – ez)
We find the poles by putting the denominator equals to zero.
That means-
1 – ez = 0
ez = 0 = ( cos 2n π + i sin 2n π) = e2nπi
z = 2nπi(n = 0, ±1, ±2, ….)
z = 2n π i is a simple pole
Example: Determine the poles of the function-
f(z) = 1/(z4 +1)
Sol.
Here we have-
f(z) = 1/(z4+1)
We find the poles by putting the denominator of the function equals to zero-
We get-
z4 + 1 = 0 and z4 = - 1
f(z) = a0 + a1(z – a) + a2(z – a)2 + . . . + b1/z - a
By De Moivre’s theorem-
Sin 1/z = 1/z – 1/3!z3 + 1/5!z5 + . ….+ (-1)n 1/(2n+1)! z2n+1
z = (-1)1/4 = (cos π + i sin π)1/4
If n = 0, then pole-
= [ cos (2n + 1)π + i sin (2n + 1)π]1/4
If n = 1, then pole-
= [ cos (2n + 1)π/4 + i sin (2n+1)π/4]
If n = 2, then pole-
z = [ cos π/4 + i sin π/4] = (1/2 + i 1/2)
If n = 3, then pole-
z = [ cos 3π/4 + i sin 3π/4] = (- 1/2 + i 1/2)
Let 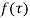 be analytic at all points within a circle
be analytic at all points within a circle 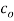 with centre
with centre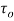 and radius
and radius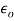 . Then
. Then
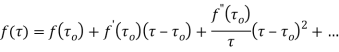
Example: Expand the function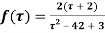
In a Taylor's series about the point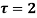
Ans. Using partial fraction method
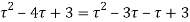
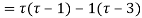
(τ-1)(τ-3)
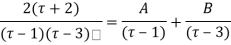
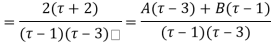
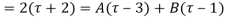
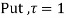
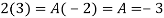
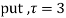
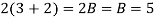
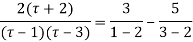
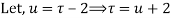
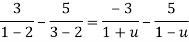
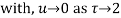
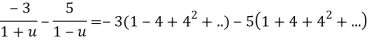
Both series converge when |4|<1
Therefore 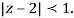 The series converges in the circle centred at
The series converges in the circle centred at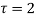 with radius of 1.
with radius of 1.
Taylor’s series expansion is
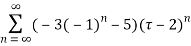
Example: Show that when 0<|z|<4
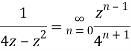
Solution When |z|<4 we have
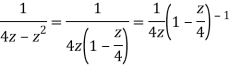
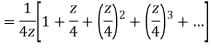
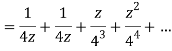
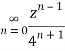
Example: Expand 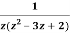 for the regions
for the regions
- 0<|z|<1
- 1<|z|<2
- |z|>2
Solution Let 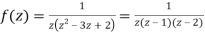
Hence resolving into partial functions we get
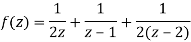
1) For 0<|z|<1 we have
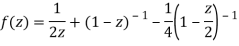
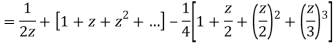
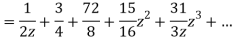
2) For 1<|z|<2 we have
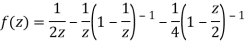
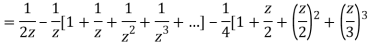
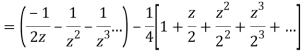
3) For |z|>2 we have
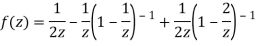
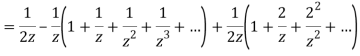
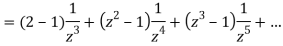
Let 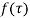 be analytic in the ring shaped region D bounded by two concentric circles
be analytic in the ring shaped region D bounded by two concentric circles 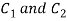 with centre
with centre 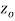 and radii
and radii 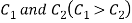 and let be any point of D. Then
and let be any point of D. Then

Example: using Taylor's series
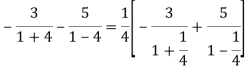
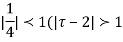

Example: Obtain the Taylor’s and Laurent’s series which represents the function 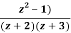 in the regions
in the regions
1) |z|<2
2) 2<|z|<3
3) |z|>3
Solution We have
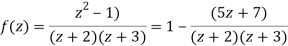
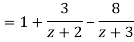
1) For |z|<2 we have

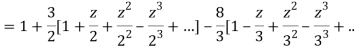
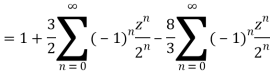

Which is Taylor’s series valid for |z|<2
2) For 2<|z|<3 we have
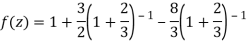
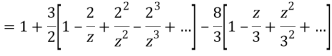
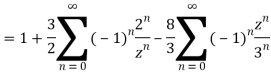
3) For |z|<3
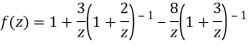
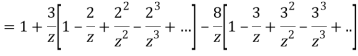
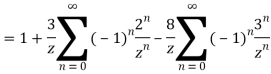
Let be a pole of order m of a function
be a pole of order m of a function and
and 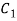 circle of radius r with centre at
circle of radius r with centre at 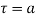 which does not contain any other singularities except at
which does not contain any other singularities except at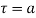 then
then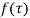 is analytic within the
is analytic within the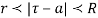 can be expanded by Laurent’s series
can be expanded by Laurent’s series
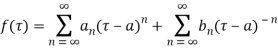
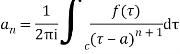
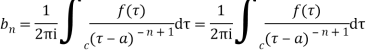
The coefficient of 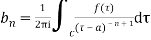 is called residue of
is called residue of 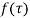 at the pole then
at the pole then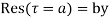
Method of finding residue
(1) If 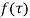 has a simple pole at
has a simple pole at 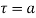 then
then 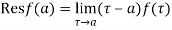
(2) If is of the form

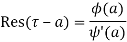
(3) If  has a pole of order n at
has a pole of order n at 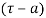 then
then
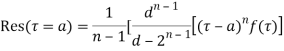
(4) Residue at a pole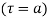 of any order
of any order

(5) Residue of 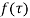 at
at 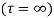
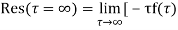
Example: Find residue of the function
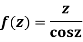
Answer
Let 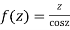
The singularities of f(z) are given by 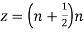
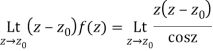
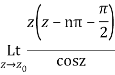
Which is of the form 
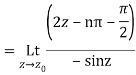
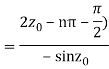
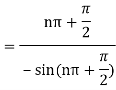
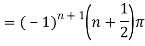
Example: Find the residue of 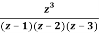 at z=1
at z=1
Answer
Let f(z)=
The poles of f(z) are determined by putting the denominator equal to zero
(z-1)(z-2)(z-3)=0
Z=1,2,3
Residue of f(z) at z=1=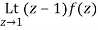
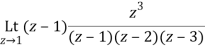
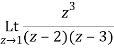
=1/2
Example: Find the residue of 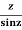
Answer
f(z)=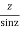
Poles are determined by putting sinz=0=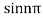
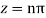
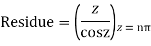
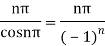
Hence the residue of the given function at pole 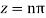 is
is 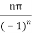
If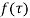 is analytic in a closed curve c except at a finite number of poles within c then
is analytic in a closed curve c except at a finite number of poles within c then
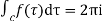 [Sum of residue at the pole within c]
[Sum of residue at the pole within c]
Example: Evaluate the following integral using residue theorem
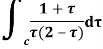
Where c is the circle.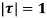 .
.
Ans.
The poles of the integral are given by putting the denominator equal to zero
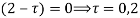
The integral is analytic on 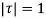 and all points inside except
and all points inside except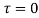 as a pole at
as a pole at 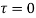 is inside the circle
is inside the circle
Hence by residue theorem
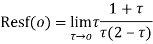
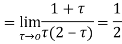
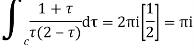
Example: Evaluate 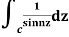 where c;|z|=4
where c;|z|=4
Answer
Here f(z)=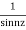
Poles are 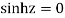
Sin iz=0

Poles 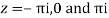
Lie inside the circle |z|=4
The given function 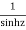 is of the form
is of the form 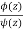
Its pole at z=a is 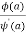
Residue (at 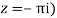
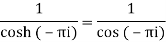
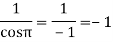
Residue at z=0=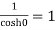
Residue at 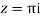 =
=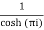
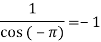
Residue at  are
are
Respectively -1,1 and -1
Hence the required integrand
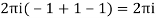
Example: Evaluate 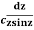 :c is the unit circle about the origin
:c is the unit circle about the origin
Answer
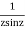 =
=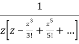
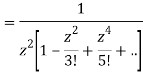
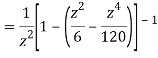

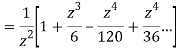
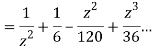
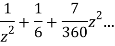
This shows that z=0 is a pole of order 2 for the function 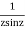 and the residue of the poles is zero(coefficient of 1/z)
and the residue of the poles is zero(coefficient of 1/z)
Now the pole at z=0 lies within c
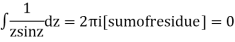
Example: Evaluation of definite integral
Show that 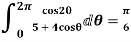
Solution
I= 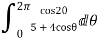
Real part of 
Now I= 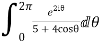 =
=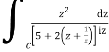
Putting z=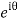 where c is the unit circle |z|=1
where c is the unit circle |z|=1
I=
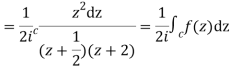
Now f(z) has simple poles at 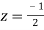 and z=-2 of which only
and z=-2 of which only 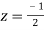 lies inside c.
lies inside c.
Residue at 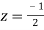 is
is 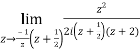
=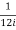
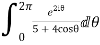 =
=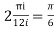
Now equating real parts on both sides we get
I=
Example: Prove that 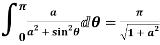
Solution
Let 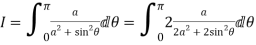
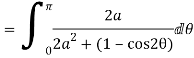
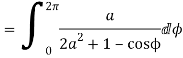
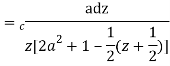
Putting 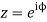 where c is the unit circle |z|=1
where c is the unit circle |z|=1
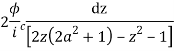
2ai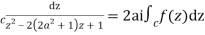
Poles of f(z) are given by the roots of
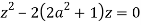
Or 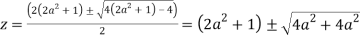
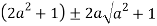
Let 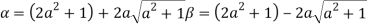
Clearly 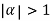 and since
and since 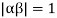 we have
we have 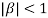 Hence the only pole inside c is at z=
Hence the only pole inside c is at z=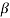
Residue (at 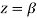 )
)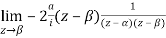
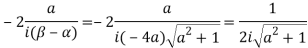
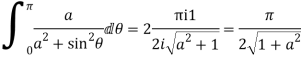

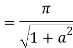
Example: Evaluate 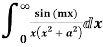
Answer
Consider 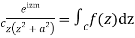
Where c is the closed contour consisting of
1) Real axis from 
2) Large semicircle in the upper half plane given by |z|=R
3) The real axis -R to 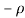 and
and
4) Small semicircle given by |z|=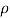
Now f(z) has simple poles at z=0  of which only z=
of which only z=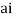 is avoided by indentation
is avoided by indentation
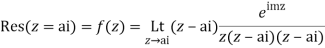
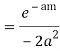
Hence by Cauchy’s Residue theorem
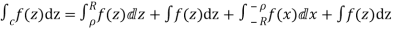
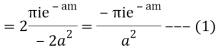
Since  and
and
Hence by Jordan’s Lemma 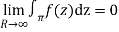
Also since 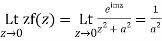
Hence 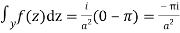
Hence as 

Equating imaginary parts we get
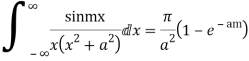
Example: Prove that 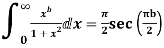
Solution
Consider 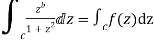
Where c is the contour consisting of a large semicircle in the upper half plane indented at the origin as shown in the figure
Here we have avoided the branch point o, of 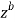 by indenting the origin
by indenting the origin
Then only simple of f(z) within c is at z=i
The residue(at z=i) =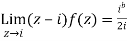
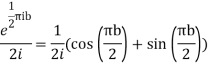
Hence by residue theorem
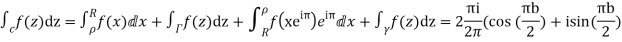
Since  on -ve real axis.
on -ve real axis.
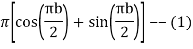
Now 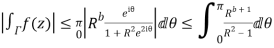
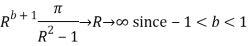
Similarly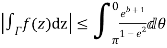
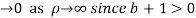
Hence when 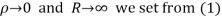
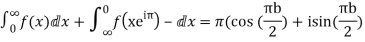
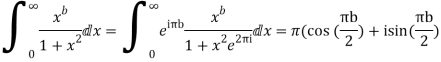
Equating real parts we get
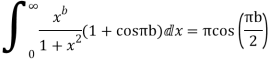
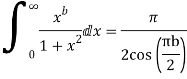
Fourier Integral: Improper Integral Involving Trigonometric Functions
The integrals
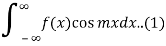
Can be evaluated by integrating
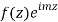
By residue theorem
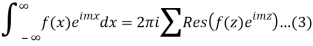
Where the summation extends to all poles of 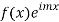 in the upper half=plane (since |
in the upper half=plane (since |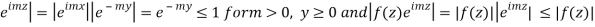 it follows that
it follows that
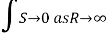
Equating the real and imaginary
Parts of (3), we get
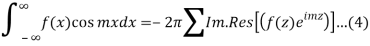
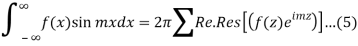
Example: Evaluate-
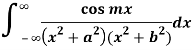
Sol:
We know that  atits poles in the upper half plane. So consider
atits poles in the upper half plane. So consider
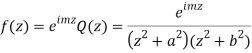
(z) has simple poles at z = ±ai, z = ±bi out of which z = ai, bi lies in the upper half plane.
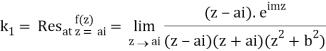
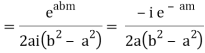
Similarly,
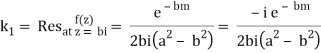
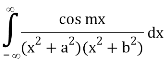
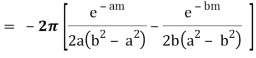

Example: Evaluate:

Sol:
We know that  atits poles in the upper half plane.
atits poles in the upper half plane.
So consider 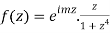 which has singular points at z =
which has singular points at z = 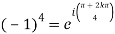 for k = 0, 1, 2, 3. Out of these four, only
for k = 0, 1, 2, 3. Out of these four, only 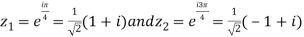 lies in the
lies in the
Upper half plane.
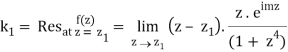
Which is 0/0 form, Applying L’ Hostpital’s rule
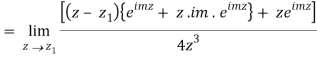
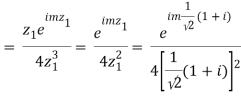

Real part of k1 = ¼ e-m/2 . Sin m/2
Similarly
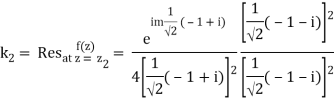
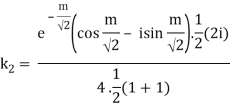
Real part of k2 = ¼ e- m/2 . Sin m/2
Then
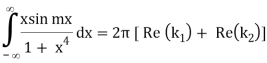

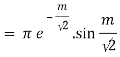
References:
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
Unit - 5
Complex Variable - Integration
Contour integration is the process of calculating the values of a contour integral around a given contour in the complex plane.
Example: Solve 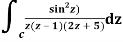 where
where 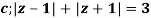
Answer
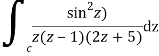
Where 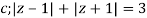
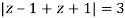
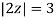
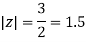
Poles of the inter are given by putting the denominator equal to zero.
Z(z-1)(2z+5)=0
Z=0,1,-5/2
The integrand has three simple poles at
Z=0,1,-5/2
The given circle |z|=3/2 with centre at z=0 and radius =3/2 encloses two poles z=0 and 1
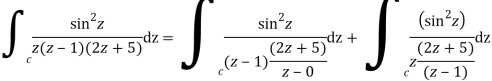
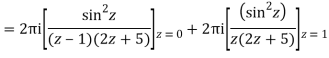
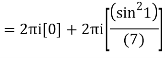
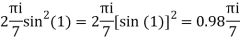
Example: Solve 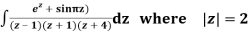
Answer
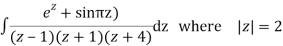
Poles are
|z-0|=2
Poles 1 and -1 inside the circle
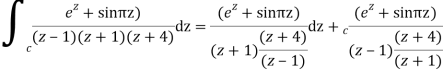
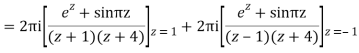
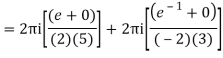
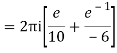
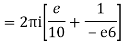
Derivation of Cauchy Integral theorem:
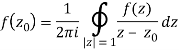
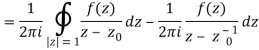
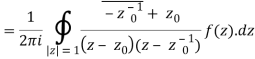
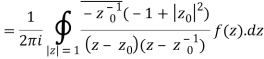
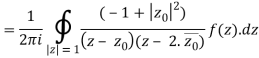
Example 1:
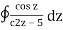 where C = | z – 3| = 2
where C = | z – 3| = 2
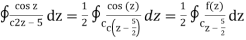 where f(z) = cosz
where f(z) = cosz
= ½ (2 πi) f(5/2) by cauchy’s integral formula
= πi. Cos (5/2)
Example 2:
Solve the following by cauchy’s integral method:
f(n)(a) = n!/2πi 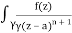
Solution:
Given,
f(n)(a) = n!/2πi 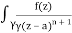
f(k + 1)(a) = d/da f(k)(a)
= k!/2πi 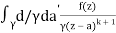
= k!/2πi 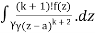
= (k+1)!/2πi 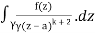
Cauchy’s integral formula-
Cauchy’s integral formula can be defined as-
f(a) = 1/2πi 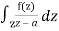
Where f(z) is analytic function within and on closed curve C, a is any point within C.
Example-1: Evaluate 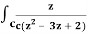 dz by using Cauchy’s integral formula.
dz by using Cauchy’s integral formula.
Here c is the circle |z - 2| = 1/2
Sol. It is given that-
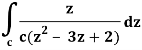
Find its poles by equating denominator equals to zero.
z2 – 3z + 2 = 0
(z – 1)(z – 2) = 0
z = 1, 2
There is one pole inside the circle, z = 2,
So that-


Now by using Cauchy’s integral formula, we get-
= 2πi [ z / z-1]z = 2 = 2πi(2/2 -1) = 4πi
Example-2: Evaluate the integral given below by using Cauchy’s integral formula-

Sol. Here we have-
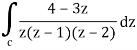
Find its poles by equating denominator equals to zero.
z(z – 1)(z – 2) = 0
We get-
z = 0,1, 2
There are two poles in the circle-
Z = 0 and z = 1
So that-
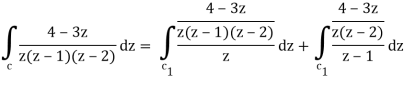 = 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2πi . 4/(-1)(-2) + 2πi (4 -3)/1(1 -2) = 2πi(2 – 1) = 2πi
Example-3: Evaluate 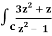 dz if c is circle |z - 1| = 1.
dz if c is circle |z - 1| = 1.
Sol. Here we have-
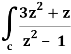
Find its poles by equating denominator equals to zero.
z2 – 1 = 0 or z2 = 1 or z = ± 1
The given circle encloses a simple pole at z = 1.
So that-
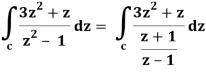 = 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 4πi
The value of z is said to be zero of the analytic function f(z) when f(z) = 0.
If f(z) is analytic in the neighbourhood of z = a, then by Taylor’s theorem-
f(z) = a0 + a1(z – a) + a2(z – a)2 + a3(z – a)3 + . . . + an(z – a)n+ . . .
If a0 = a1 = a2 = . . . = an – 1 = 0 but an is non- zero, then f(z) is said to have a zero of order n at z = a.
The zero is said to be simple if n = 1.
an = fn(a)/n!
For a zero of order m at z = a,
f(a) = f’(a) = f”(a) = fn – 1(a) = 0 but fn(a) ≠ 0
Thus in the neighbourhood of the zero at z = a of order n
f(z) = an(z – a)n + an+1 (z – a)n + 1 = (z – a)n [ an + an+1(z –a) + …] = (z – a)n ∅(z)
Where ∅(z) = an + an+1 (z – a) + . . . Is analytic and non-zero at and in the neighbourhood of z = a.
Example: Find out the zero of the following-
f(z) = (z – 2)/z2 sin 1/(z – 1)
Sol. Zeroes of the function-
f(z) = 0
(z – 2)/z2 sin 1/(z – 1) = 0
(z – 2)/z2 = 0, sin 1/(z – 1) = 0
z = 2, 1/(z – 1) = nπ ( n = 0, ±1, ±2 ….)
z = 2, 1 + 1/nπ (n = 0, ±1, ±2 ….)
Key takeaways-
- The pole is said to be simple pole when m = 1.
- Cauchy’s residue theorem-
If f(z) is analytic in a closed curve C, except at a finite number of poles within C, then-
z = [ cos 5π/4 + i sin 5π/4] = ( - 1/2 – i 1/2)
A point at which a function f(z) is not analytic is known as a singular point or singularity of the function.
Isolated singular point- If z = a is a singularity of f(z) and if there is no other singularity within a small circle surrounding the point z = a, then z = a is said to be an isolated singularity of the function f (z); otherwise it is called non-isolated.
Pole of order m- Suppose a function f(z) have an isolated singular point z = a, f(z) can be expanded in a Laurent’s series around z = a, giving
= 2πi [ (4 – 3z)/(z – 1)(z – 2)]z = 0 + 2πi [(4 – 3z)/z(z -2)]z = 1
= 2πi. 4/(-1)(-2) + 2πi . (4 – 3)/1(1 – 2) = 2πi(2 – 1) = 2πi …….(1)
In some cases it may happen that the coefficient bm + 1 = bm + 2 = bm + 3 = 0 , then equation (1) becomes-
= 2πi[(3z2+z)/(z+1)]z = 1 = 2πi(3+1)/(1+1)
f(z) = a0 + a1(z – a) + a2(z – a)2 + . . . + b1/(z – a) + b2/(z – a)2 + . . .+ bm/(z – a)m+ bm+1/(z – a)m +1 + bm+2/(z – a)m+2 + . . .
Then z = a is said to be a pole of order m of the function f(z).
Note- The pole is said to be simple pole when m = 1.
In this case-
f(z) = a0 + a1(z – a) + a2(z – a)2 + . . . + b1/(z – a) + b2/(z – a)2 + . . .+ bm/(z – a)m
Working steps to find singularity-
Step-1: If  exists and it is finite then z = a is a removable singular point.
exists and it is finite then z = a is a removable singular point.
Step-2: If 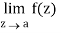 does not exists then z = a is an essential singular point.
does not exists then z = a is an essential singular point.
Step-3: If 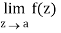 is infinite then f(z) has a pole at z = a. The order of the pole is same as the number of negative power terms in the series expansion of f(z).
is infinite then f(z) has a pole at z = a. The order of the pole is same as the number of negative power terms in the series expansion of f(z).
Example: Find the singularity of the function-
f(z) = sin 1/z
Sol.
As we know that-f(z) = a0 +a1(z – a) + a2(z – a)2 + . . . + 1/(z – a)m[ b1(z – a)m – 1 + b2(z – a)m – 2 + b3(z – a)m – 3 + . . . + bm}
So that there is a number of singularity.
Sin 1/z is not analytic at z = a
(1/z = ∞ at z = 0)
Example: Find the singularity of 1/(1 – ez) at z = 2πi
Sol.
Here we have-
f(z) = 1/(1 – ez)
We find the poles by putting the denominator equals to zero.
That means-
1 – ez = 0
ez = 0 = ( cos 2n π + i sin 2n π) = e2nπi
z = 2nπi(n = 0, ±1, ±2, ….)
z = 2n π i is a simple pole
Example: Determine the poles of the function-
f(z) = 1/(z4 +1)
Sol.
Here we have-
f(z) = 1/(z4+1)
We find the poles by putting the denominator of the function equals to zero-
We get-
z4 + 1 = 0 and z4 = - 1
f(z) = a0 + a1(z – a) + a2(z – a)2 + . . . + b1/z - a
By De Moivre’s theorem-
Sin 1/z = 1/z – 1/3!z3 + 1/5!z5 + . ….+ (-1)n 1/(2n+1)! z2n+1
z = (-1)1/4 = (cos π + i sin π)1/4
If n = 0, then pole-
= [ cos (2n + 1)π + i sin (2n + 1)π]1/4
If n = 1, then pole-
= [ cos (2n + 1)π/4 + i sin (2n+1)π/4]
If n = 2, then pole-
z = [ cos π/4 + i sin π/4] = (1/2 + i 1/2)
If n = 3, then pole-
z = [ cos 3π/4 + i sin 3π/4] = (- 1/2 + i 1/2)
Let 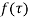 be analytic at all points within a circle
be analytic at all points within a circle 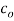 with centre
with centre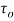 and radius
and radius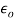 . Then
. Then
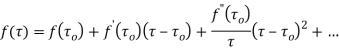
Example: Expand the function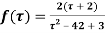
In a Taylor's series about the point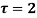
Ans. Using partial fraction method

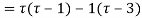
(τ-1)(τ-3)
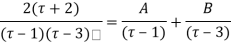
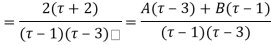

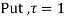
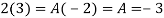


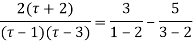
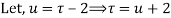
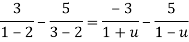
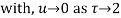

Both series converge when |4|<1
Therefore 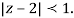 The series converges in the circle centred at
The series converges in the circle centred at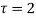 with radius of 1.
with radius of 1.
Taylor’s series expansion is
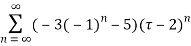
Example: Show that when 0<|z|<4
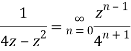
Solution When |z|<4 we have
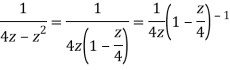
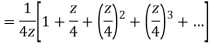
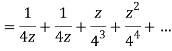

Example: Expand 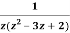 for the regions
for the regions
- 0<|z|<1
- 1<|z|<2
- |z|>2
Solution Let 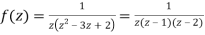
Hence resolving into partial functions we get
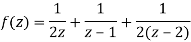
1) For 0<|z|<1 we have
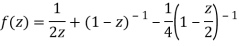
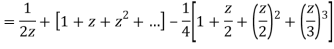
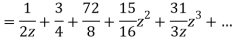
2) For 1<|z|<2 we have
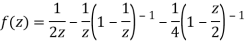
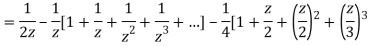

3) For |z|>2 we have
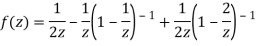
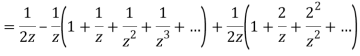
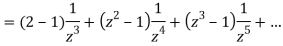
Let 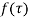 be analytic in the ring shaped region D bounded by two concentric circles
be analytic in the ring shaped region D bounded by two concentric circles 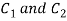 with centre
with centre 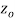 and radii
and radii 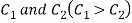 and let be any point of D. Then
and let be any point of D. Then
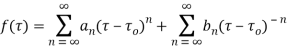
Example: using Taylor's series


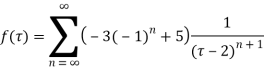
Example: Obtain the Taylor’s and Laurent’s series which represents the function 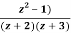 in the regions
in the regions
1) |z|<2
2) 2<|z|<3
3) |z|>3
Solution We have
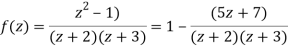
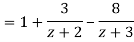
1) For |z|<2 we have
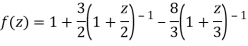
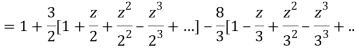
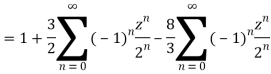
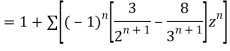
Which is Taylor’s series valid for |z|<2
2) For 2<|z|<3 we have
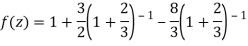
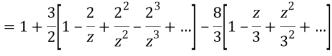

3) For |z|<3
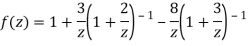
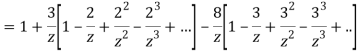
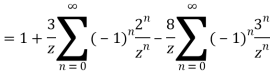
Let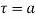 be a pole of order m of a function
be a pole of order m of a function and
and  circle of radius r with centre at
circle of radius r with centre at 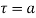 which does not contain any other singularities except at
which does not contain any other singularities except at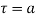 then
then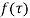 is analytic within the
is analytic within the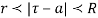 can be expanded by Laurent’s series
can be expanded by Laurent’s series

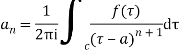
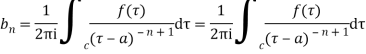
The coefficient of 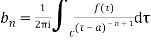 is called residue of
is called residue of 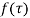 at the pole then
at the pole then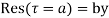
Method of finding residue
(1) If 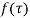 has a simple pole at
has a simple pole at 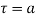 then
then 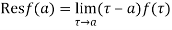
(2) If is of the form
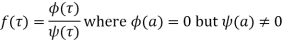
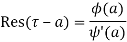
(3) If 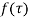 has a pole of order n at
has a pole of order n at 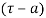 then
then
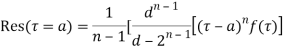
(4) Residue at a pole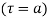 of any order
of any order
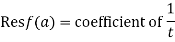
(5) Residue of 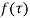 at
at 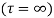
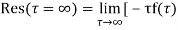
Example: Find residue of the function
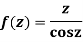
Answer
Let 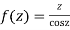
The singularities of f(z) are given by 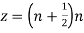
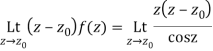
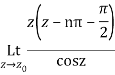
Which is of the form 
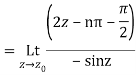
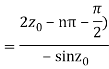
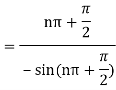
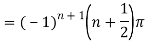
Example: Find the residue of 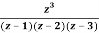 at z=1
at z=1
Answer
Let f(z)=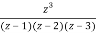
The poles of f(z) are determined by putting the denominator equal to zero
(z-1)(z-2)(z-3)=0
Z=1,2,3
Residue of f(z) at z=1=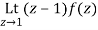
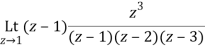
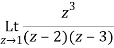
=1/2
Example: Find the residue of 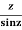
Answer
f(z)=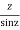
Poles are determined by putting sinz=0=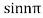
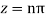

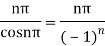
Hence the residue of the given function at pole 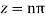 is
is 
If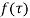 is analytic in a closed curve c except at a finite number of poles within c then
is analytic in a closed curve c except at a finite number of poles within c then
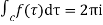 [Sum of residue at the pole within c]
[Sum of residue at the pole within c]
Example: Evaluate the following integral using residue theorem
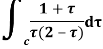
Where c is the circle.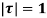 .
.
Ans.
The poles of the integral are given by putting the denominator equal to zero
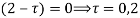
The integral is analytic on  and all points inside except
and all points inside except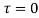 as a pole at
as a pole at 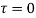 is inside the circle
is inside the circle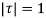
Hence by residue theorem
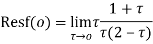
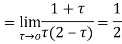
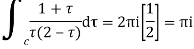
Example: Evaluate 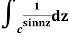 where c;|z|=4
where c;|z|=4
Answer
Here f(z)=
Poles are 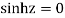
Sin iz=0
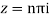
Poles 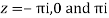
Lie inside the circle |z|=4
The given function 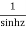 is of the form
is of the form 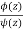
Its pole at z=a is 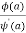
Residue (at 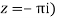
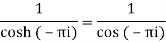
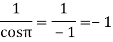
Residue at z=0=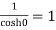
Residue at 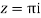 =
=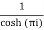
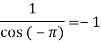
Residue at 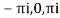 are
are
Respectively -1,1 and -1
Hence the required integrand
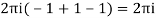
Example: Evaluate 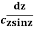 :c is the unit circle about the origin
:c is the unit circle about the origin
Answer
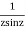 =
=
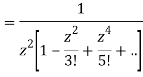
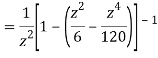
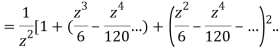
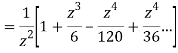
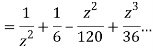
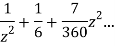
This shows that z=0 is a pole of order 2 for the function 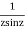 and the residue of the poles is zero(coefficient of 1/z)
and the residue of the poles is zero(coefficient of 1/z)
Now the pole at z=0 lies within c
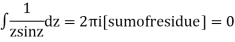
Example: Evaluation of definite integral
Show that 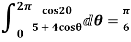
Solution
I= 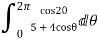
Real part of 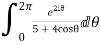
Now I= 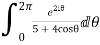 =
=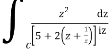
Putting z=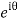 where c is the unit circle |z|=1
where c is the unit circle |z|=1
I=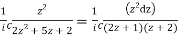
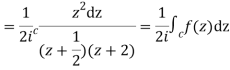
Now f(z) has simple poles at 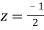 and z=-2 of which only
and z=-2 of which only 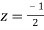 lies inside c.
lies inside c.
Residue at 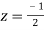 is
is 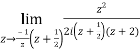
=
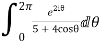 =
=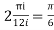
Now equating real parts on both sides we get
I=
Example: Prove that 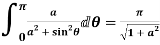
Solution
Let 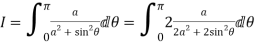
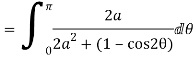
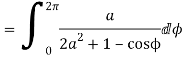
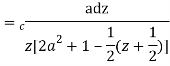
Putting 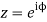 where c is the unit circle |z|=1
where c is the unit circle |z|=1

2ai
Poles of f(z) are given by the roots of

Or 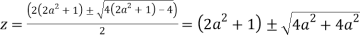
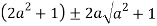
Let 
Clearly 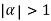 and since
and since 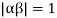 we have
we have 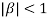 Hence the only pole inside c is at z=
Hence the only pole inside c is at z=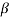
Residue (at 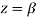 )
)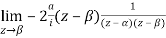
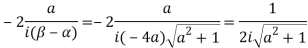
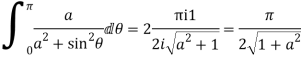

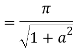
Example: Evaluate 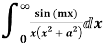
Answer
Consider 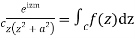
Where c is the closed contour consisting of
1) Real axis from 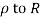
2) Large semicircle in the upper half plane given by |z|=R
3) The real axis -R to 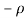 and
and
4) Small semicircle given by |z|=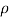
Now f(z) has simple poles at z=0 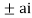 of which only z=
of which only z=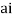 is avoided by indentation
is avoided by indentation
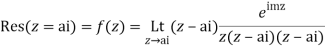
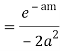
Hence by Cauchy’s Residue theorem
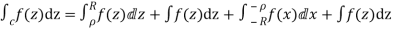
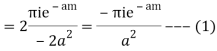
Since 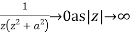 and
and
Hence by Jordan’s Lemma 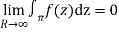
Also since 
Hence 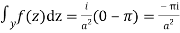
Hence as 
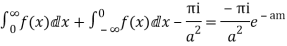
Equating imaginary parts we get
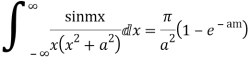
Example: Prove that 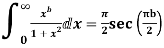
Solution
Consider 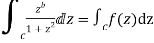
Where c is the contour consisting of a large semicircle in the upper half plane indented at the origin as shown in the figure
Here we have avoided the branch point o, of 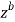 by indenting the origin
by indenting the origin
Then only simple of f(z) within c is at z=i
The residue(at z=i) =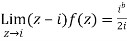
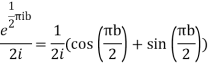
Hence by residue theorem
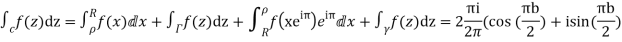
Since 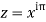 on -ve real axis.
on -ve real axis.
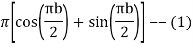
Now 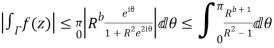
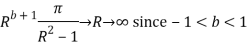
Similarly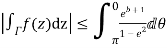
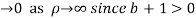
Hence when 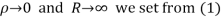
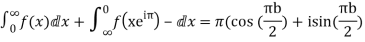
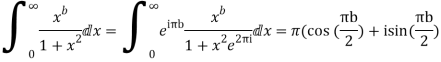
Equating real parts we get
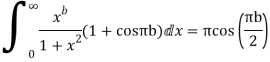
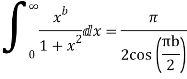
Fourier Integral: Improper Integral Involving Trigonometric Functions
The integrals
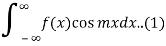
Can be evaluated by integrating
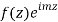
By residue theorem
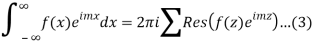
Where the summation extends to all poles of  in the upper half=plane (since |
in the upper half=plane (since |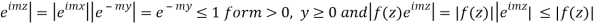 it follows that
it follows that
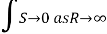
Equating the real and imaginary
Parts of (3), we get
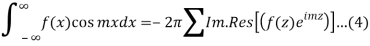
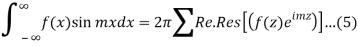
Example: Evaluate-
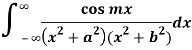
Sol:
We know that 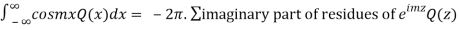 atits poles in the upper half plane. So consider
atits poles in the upper half plane. So consider
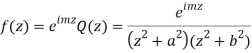
(z) has simple poles at z = ±ai, z = ±bi out of which z = ai, bi lies in the upper half plane.
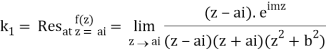
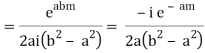
Similarly,
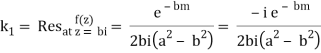
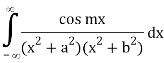
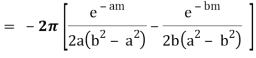
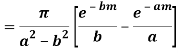
Example: Evaluate:
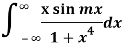
Sol:
We know that  atits poles in the upper half plane.
atits poles in the upper half plane.
So consider  which has singular points at z =
which has singular points at z =  for k = 0, 1, 2, 3. Out of these four, only
for k = 0, 1, 2, 3. Out of these four, only 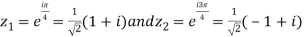 lies in the
lies in the
Upper half plane.
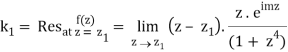
Which is 0/0 form, Applying L’ Hostpital’s rule
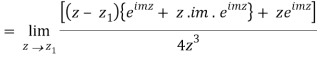
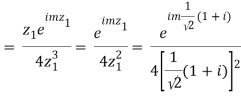

Real part of k1 = ¼ e-m/2 . Sin m/2
Similarly
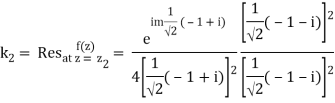
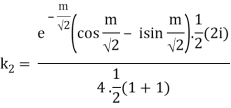
Real part of k2 = ¼ e- m/2 . Sin m/2
Then
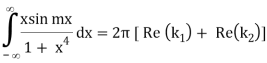
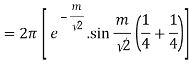
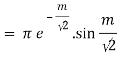
References:
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010