Unit - 1
Basic concepts and notations
A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively. Arrays, Linked Lists, Stacks, Queues, and other Data Structures are examples. Data Structures are employed in practically every element of computer science, including operating systems, compiler design, artificial intelligence, graphics, and many more applications.
Data Structures are an important aspect of many computer science algorithms because they allow programmers to efficiently handle data. It is critical to improving the performance of a software or program because the software's primary duty is to save and retrieve user data as quickly as feasible.
Basic terminology
The building blocks of every program or software are data structures. The most challenging challenge for a programmer is deciding on a suitable data structure for a program. When it comes to data structures, the following terminology is utilized.
Data: The data on a student can be defined as an elementary value or a set of values, for example, the student's name and id.
Group items: Group items are data items that include subordinate data items, such as a student's name, which can have both a first and a last name.
Record: A record can be characterized as a collection of several data objects. For example, if we consider the student entity, the name, address, course, and grades can all be gathered together to constitute the student's record.
File: A file is a collection of various records of one type of entity; for example, if there are 60 employees in the class, the relevant file will contain 20 records, each containing information about each employee.
Attribute and Entity: A class of objects is represented by an entity. It has a number of characteristics. Each attribute represents an entity's specific property.
Operations
- Traversing
The set of data elements is present in every data structure. Traversing a data structure is going through each element in order to perform a certain action, such as searching or sorting.
For example, if we need to discover the average of a student's grades in six different topics, we must first traverse the entire array of grades and calculate the total amount, then divide that sum by the number of subjects, which in this case is six, to find the average.
2. Insertion
The process of adding elements to the data structure at any position is known as insertion.
We can only introduce n-1 data elements into a data structure if its size is n.
3. Deletion
Deletion is the process of eliminating an element from a data structure. We can remove an element from the data structure at any point in the data structure.
Underflow occurs when we try to delete an element from an empty data structure.
4. Searching
Searching is the process of discovering an element's location within a data structure. There are two types of search algorithms: Linear Search and Binary Search.
5. Sorting
Sorting is the process of putting the data structure in a specified order. Sorting can be done using a variety of algorithms, such as insertion sort, selection sort, bubble sort, and so on.
6. Merging
Merging occurs when two lists, List A and List B, of size M and N, respectively, containing comparable types of elements are combined to form a third list, List C, of size (M+N).
Key takeaway
A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively.
Arrays, Linked Lists, Stacks, Queues, and other Data Structures are examples.
Data Structures are an important aspect of many computer science algorithms because they allow programmers to efficiently handle data.
We will go through some of the mathematical notations and tools that will be used throughout the book, such as logarithms, big-Oh notation, and probability theory.
Exponentials and Logarithms
The number $ b$ raised to the power of x is denoted by the expression bx. If $ x$ is a positive integer, the value of b multiplied by itself x-1 times is:
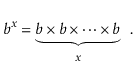
bx =1/b-x when x is a negative integer. When x equals 0, bx =1. When b is not an integer, exponentiation can still be expressed in terms of the exponential function ex, which is defined in terms of the exponential series, although this is best left to a calculus textbook.
The base- b logarithm of k is denoted by the phrase logb k. That is, the one and only x value that fulfills.
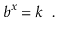
The base 2 logarithms make up the majority of the logarithms in this book (binary logarithms). We ignore the base for these, thus log k is shorthand for log2 k.
Think of logb k as the number of times we have to divide k by b before the result is less than or equal to 1. This is an informal but effective method of thinking about logarithms. When using binary search, for example, each comparison reduces the number of possible solutions by a factor of two. This process is continued until only one possible response remains. When there are at most n+1 potential responses, the number of comparisons performed using binary search is at most [log2 (n+1)].
The natural logarithm is another logarithm that appears multiple times. To express loge k, we use the notation ln k, where e, Euler's constant, is provided by
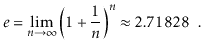
The natural logarithm is commonly mentioned because it is the value of a widely used integral:
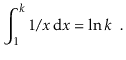
Removing logarithms from an exponent is one of the most common operations using them:
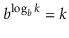
And modifying a logarithm's base:
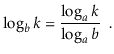
These two modifications, for example, can be used to compare natural and binary logarithms.
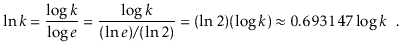
Asymptotic notations
When we look at data structures in this book, we'll talk about how long various operations take. Of course, the exact running timings will vary from computer to computer and even from run to run on a same computer. When we talk about an operation's running time, we're talking to the number of computer instructions executed during that period. Even with basic code, calculating this figure precisely can be tricky. As a result, rather than examining running times precisely, we'll employ the so-called big-Oh notation: O(f(n)) denotes a set of functions for a function f(n).
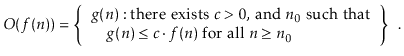
This collection comprises functions g(n) where c. f(n) begins to dominate g(n) when n is large enough.
To simplify functions, we usually employ asymptotic notation. For example, we can write O(nlog n) instead of 5n log n + 8n - 200. This is demonstrated as follows:
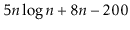
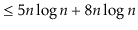
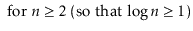
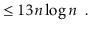
Using the constants c=13 and n 0 = 2, this shows that the function f(n)=5nlog n + 8n - 200 is in the set O(nlog n).
Big-Oh notation isn't new or exclusive to the field of computer science. It was first used in 1894 by number theorist Paul Bachmann, and it is extremely valuable for defining the execution periods of computer algorithms. Take a look at the following code:
Void snippet() {
For (int i = 0; i < n; i++)
a[i] = i;
}
One execution of this method involves
● 1 assignment ( int i = 0 ),
● n +1 comparisons ( i < n ),
● n increments ( i ++ ),
● n array offset calculations ( a [i] ), and
● n indirect assignments ( a [i] = i ).
As a result, this running time may be written as
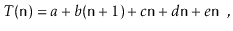
Where a, b, c, d, and e are machine-dependent constants that indicate the time it takes to conduct assignments, comparisons, increment operations, array offset calculations, and indirect assignments, respectively. If, on the other hand, this expression represents the execution time of two lines of code, then this type of analysis will clearly be unsuitable for complex code or algorithms. The running time can be simplified to using big-Oh notation.
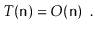
This is not only more compact, but it also provides roughly the same amount of information. Because the running time in the previous example is dependent on the constants a, b, c, d, and e, it will be impossible to compare two running times to see which is quicker without knowing the values of these constants. Even if we put forth the effort to identify these constants (for example, through timing tests), our conclusion will be valid only for the system on which we conducted our tests.
Big-Oh notation enables us to reason at a much higher level, allowing us to examine more complex functions. We won't know which algorithm is faster if both have the same big-Oh running time, and there may not be a clear winner. One might be faster on one machine, while the other might be quicker on another. If the two algorithms have measurably different big-Oh running times, we can be confident that the one with the shorter running time will be faster for large enough n values.
Factorial
The product of the positive numbers 1 to n is denoted by n!. n! stands for 'n factorial,' i.e.
n! = 1 * 2 * 3 * ….. * (n-2) * (n-1) * n
Example
4! = 1 * 2 * 3 * 4 = 24
5! = 5 * 4! = 120
Randomization and Probability
Some of the data structures described in this book are randomized; they make random decisions regardless of the data they contain or the operations they execute. As a result, doing the same set of actions with these structures multiple times may result in varying running times. We're interested in the average or expected execution times of these data structures when we examine them.
We wish to investigate the predicted value of the running time of an operation on a randomized data structure, which is a random variable. The expected value of a discrete random variable X taking on values in some countable universe U is given by the formula E[X].
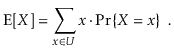
The probability that the event E occurs is denoted by PrE. These probabilities are solely applied to the randomized data structure's random selections in this book; there is no assumption that the data contained in the structure, or the sequence of operations done on the data structure, is random.
The linearity of expectation is one of the most essential features of expected values. If X and Y are two random variables,
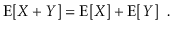
More generally, for any random variables X1,........,Xk,
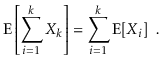
We can break down sophisticated random variables (such the left hand sides of the preceding equations) into sums of smaller random variables thanks to linearity of expectation (the right hand sides).
If we consider X to be an algorithm and N to be the size of the input data, the time and space implemented by Algorithm X are the two key criteria that determine X's efficiency.
Time Factor - The time is determined or assessed by measuring the number of critical operations in the sorting algorithm, such as comparisons.
Space Factor - The space is estimated or measured by counting the algorithm's maximum memory requirements.
With respect to N as the size of input data, the complexity of an algorithm f(N) provides the running time and/or storage space required by the method.
Space complexity
The amount of memory space required by an algorithm during its life cycle is referred to as its space complexity.
The sum of the following two components represents the amount of space required by an algorithm.
A fixed component is a space needed to hold specific data and variables (such as simple variables and constants, program size, and so on) that are independent of the problem's size.
A variable part is a space that variables require and whose size is entirely dependent on the problem's magnitude. Recursion stack space, dynamic memory allocation, and so forth.
Complexity of space Any algorithm p's S(p) is S(p) = A + Sp (I) Where A is the fixed component of the algorithm and S(I) is the variable part of the algorithm that is dependent on the instance characteristic I. Here's a basic example to help you understand the concept.
Algorithm
SUM(P, Q)
Step 1 - START
Step 2 - R ← P + Q + 10
Step 3 - Stop
There are three variables here: P, Q, and R, as well as one constant. As a result, S(p) = 1+3. Now, the amount of space available is determined by the data types of specified constant types and variables, and it is multiplied accordingly.
Time complexity
The time complexity of an algorithm is a representation of how long it takes for the algorithm to complete its execution. Time requirements can be expressed or specified as a numerical function t(N), where N is the number of steps and t(N) is the time taken by each step.
When adding two n-bit numbers, for example, N steps are taken. As a result, the total processing time is t(N) = c*n, where c represents the time spent adding two bits. We can see that as the input size grows, t(N) climbs linearly.
Time space trade off
- It is also known as time memory tradeoff.
- It is a way of solving problems in less time by using more storage space.
- It can be used with the problem of data storage.
- For example: time complexity of merge sort is O(n log n)in all cases. But requires an auxiliary array.
- In quick sort complexity is O(n log n) for best and average case but it doesn’t require auxiliary space.
- Two Space-for-Time Algorithm Varieties:
- Input enhancement - To store some info, preprocess the input (or its portion) to be used in solving the issue later
- Counting sorts
- String searching algorithms
- Pre-structuring-preprocessing the input to access its components
1) hashing 2) indexing schemes simpler (e.g., B-trees)
Big Oh (O) Notation:
- It is the formal way to express the time complexity.
- It is used to define the upper bound of an algorithm’s running time.
- It shows the worst-case time complexity or largest amount of time taken by the algorithm to perform a certain task.
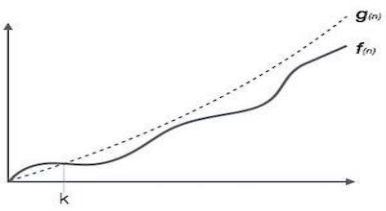
Fig 1: Big Oh notation
Here, f (n) <= g (n) …………….(eq1)
Where n>= k, C>0 and k>=1
If any algorithm satisfies the eq1 condition then it becomes f (n)= O (g (n))
Properties of Big oh notation
The definition of big O is pretty ugly to have to work with all the time, kind of like the "limit" definition of a derivative in Calculus. Here are some helpful theorems you can use to simplify big O calculations:
● Any kth degree polynomial is O(nk).
● a nk = O(nk) for any a > 0.
● Big O is transitive. That is, if f(n) = O(g(n)) and g(n) is O(h(n)), then f(n) = O(h(n)).
● logan = O(logb n) for any a, b > 1. This practically means that we don't care, asymptotically, what base we take our logarithms to. (I said asymptotically. In a few cases, it does matter.)
● Big O of a sum of functions is big O of the largest function. How do you know which one is the largest? The one that all the others are big O of. One consequence of this is, if f(n) = O(h(n)) and g(n) is O(h(n)), then f(n) + g(n) = O(h(n)).
● f(n) = O(g(n)) is true if limn->infinity f(n)/g(n) is a constant.
Key takeaway
- It is also known as a time memory tradeoff.
- It is a way of solving problems in less time by using more storage space.
We all know that as the input size (n) grows, the running time of an algorithm grows (or stays constant in the case of constant running time). Even if the input has the same size, the running duration differs between distinct instances of the input. In this situation, we examine the best, average, and worst-case scenarios. The best case running time is the shortest, the worst case running time is the longest, and the average case running time is the time required to execute the algorithm on average. All of these principles will be explained using two examples: I linear search and (ii) insertion sort.
Best case
Consider the case of Linear Search, in which we look for a certain item in an array. We return the relevant index if the item is in the array; else, we return -1. The linear search code is provided below.
Int search(int a, int n, int item) {
Int i;
For (i = 0; i < n; i++) {
If (a[i] == item) {
Return a[i]
}
}
Return -1
}
Variable an is an array, n is the array's size, and item is the array item we're looking for. It will return the index immediately if the item we're seeking for is in the very first position of the array. The for loop is just executed once. In this scenario, the complexity will be O. (1). This is referred to be the best case scenario.
Average case
On occasion, we perform an average case analysis on algorithms. The average case is nearly as severe as the worst scenario most of the time. When attempting to insert a new item into its proper location using insertion sort, we compare the new item to half of the sorted items on average. The complexity remains on the order of n2, which corresponds to the worst-case running time.
Analyzing an algorithm's average behavior is usually more difficult than analyzing its worst-case behavior. This is due to the fact that it is not always clear what defines a "average" input for a given situation. As a result, a useful examination of an algorithm's average behavior necessitates previous knowledge of the distribution of input instances, which is an impossible condition. As a result, we frequently make the assumption that all inputs of a given size are equally likely and do the probabilistic analysis for the average case.
Worst case
In real life, we almost always perform a worst-case analysis on an algorithm. The longest running time for any input of size n is called the worst case running time.
The worst case scenario in a linear search is when the item we're looking for is at the last place of the array or isn't in the array at all. We must run through all n elements in the array in both circumstances. As a result, the worst-case runtime is O. (n). In the case of linear search, worst-case performance is more essential than best-case performance for the following reasons.
● Rarely is the object we're looking for in the first position. If there are 1000 entries in the array, start at 1 and work your way up. There is a 0.001% probability that the item will be in the first place if we search it at random from 1 to 1000.
● Typically, the item isn't in the array (or database in general). In that situation, the worst-case running time is used.
Similarly, when items are reverse sorted in insertion sort, the worst case scenario occurs. In the worst scenario, the number of comparisons will be on the order of n2, and hence the running time will be O (n2).
Knowing an algorithm's worst-case performance ensures that the algorithm will never take any longer than it does today.
Key takeaway
The best case running time is the shortest, the worst case running time is the longest, and the average case running time is the time required to execute the algorithm on average.
An array is a collection of data items, all of the same type, accessed using a common name.
A one-dimensional array is like a list; A two dimensional array is like a table; The C language places no limits on the number of dimensions in an array, though specific implementations may.
Some texts refer to one-dimensional arrays as vectors, two-dimensional arrays as matrices, and use the general term arrays when the number of dimensions is unspecified or unimportant.
Linear arrays
A one-dimensional array, often known as a single-dimensional array, is one in which a single subscript specification is required to identify a specific array element. We can declare a one-dimensional array as follows:
Data_type array_name [Expression];
Where,
Data_type - The kind of element to be stored in the array is data type.
Array_name - array name specifies the array's name; it can be any type of name, much like other simple variables.
Expression - The number of values to be placed in the array is supplied; arrays are sometimes known as subscripted values; the subscript value must be an integer value, therefore the array's subscript begins at 0.
Example:
Int "a" [10]
Where int: data type
a: array name
10: expression
Output
Data values are dummy values, you can understand after seeing the output, indexing starts from “0”.
Multidimensional Arrays
A 2D array can be defined as an array of arrays. The 2D array is organized as matrices which can be represented as the collection of rows and columns.
However, 2D arrays are created to implement a relational database look alike data structure. It provides ease of holding bulk data at once which can be passed to any number of functions wherever required.
How to declare 2D Array
The syntax of declaring a two dimensional array is very much similar to that of a one dimensional array, given as follows.
Int arr[max_rows][max_columns];
However, It produces the data structure which looks like the following.
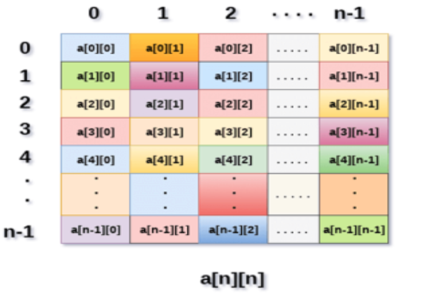
Fig 2: Example
Above image shows the two dimensional array, the elements are organized in the form of rows and columns. First element of the first row is represented by a[0][0] where the number shown in the first index is the number of that row while the number shown in the second index is the number of the column.
How do we access data in a 2D array
Due to the fact that the elements of 2D arrays can be random accessed. Similar to one dimensional arrays, we can access the individual cells in a 2D array by using the indices of the cells. There are two indices attached to a particular cell, one is its row number while the other is its column number.
However, we can store the value stored in any particular cell of a 2D array to some variable x by using the following syntax.
Int x = a[i][j];
Where i and j is the row and column number of the cell respectively.
We can assign each cell of a 2D array to 0 by using the following code:
- For ( int i=0; i<n ;i++)
- {
- For (int j=0; j<n; j++)
- {
- a[i][j] = 0;
- }
- }
Initializing 2D Arrays
We know that, when we declare and initialize a one dimensional array in C programming simultaneously, we don't need to specify the size of the array. However this will not work with 2D arrays. We will have to define at least the second dimension of the array.
The syntax to declare and initialize the 2D array is given as follows.
Int arr[2][2] = {0,1,2,3};
The number of elements that can be present in a 2D array will always be equal to (number of rows * number of columns).
Example: Storing User's data into a 2D array and printing it.
C Example:
- #include <stdio.h>
- Void main ()
- {
- Int arr[3][3],i,j;
- For (i=0;i<3;i++)
- {
- For (j=0;j<3;j++)
- {
- Printf("Enter a[%d][%d]: ",i,j);
- Scanf("%d",&arr[i][j]);
- }
- }
- Printf("\n printing the elements ....\n");
- For(i=0;i<3;i++)
- {
- Printf("\n");
- For (j=0;j<3;j++)
- {
- Printf("%d\t",arr[i][j]);
- }
- }
- }
Key takeaway
An array is a collection of data items, all of the same type, accessed using a common name.
A one-dimensional array is like a list; A two dimensional array is like a table; The C language places no limits on the number of dimensions in an array, though specific implementations may.
Arrays can be declared in a variety of ways depending on the language.

Arrays can be declared in a variety of ways depending on the language. Consider the C array declaration as an example.

The following are the key points to consider, as shown in the diagram above.
● The index begins with a zero.
● The length of the array is 10, which indicates it can hold ten elements.
● The index of each element can be used to access it. For example, an element at index 6 can be retrieved as 9.
Traversal
The traversal of an array's elements is performed with this operation.
Example
The following software walks an array and outputs its elements:
#include <stdio.h>
Main() {
Int LA[] = {1,3,5,7,8};
Int item = 10, k = 3, n = 5;
Int i = 0, j = n;
Printf("The original array elements are :\n");
For(i = 0; i<n; i++) {
Printf("LA[%d] = %d \n", i, LA[i]);
}
}
When we compile and run the preceding program, we get the following result:
Output
The original array elements are:
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8
Bubble Sort is a simple algorithm for sorting a collection of n elements that is provided in the form of an array with n elements. Bubble Sort compares each element individually and sorts them according to their values.
If an array must be sorted in ascending order, bubble sort will begin by comparing the first and second members of the array, swapping both elements if the first element is greater than the second, and then moving on to compare the second and third elements, and so on.
If there are n elements in total, we must repeat the method n-1 times.
It's called bubble sort because the largest element in the given array bubbles up to the last position or highest index with each full iteration, similar to how a water bubble rises to the sea surface.
Although it is simple to use, bubble sort is largely employed as an educational tool because its performance in the actual world is low. It isn't designed to handle huge data collections. Bubble sort has an average and worst-case complexity of O(n2), where n is the number of elements.
Sorting is done by going through all of the items one by one, comparing them to the next closest element, and swapping them if necessary.
Algorithm
Assume arr is an array of n elements in the algorithm below. The algorithm's presumed swap function will swap the values of specified array members.
Begin BubbleSort(arr)
For all array elements
If arr[i] > arr[i+1]
Swap(arr[i], arr[i+1])
End if
End for
Return arr
End BubbleSort
Working of Bubble Sort
Assume we're attempting to arrange the elements in ascending order.
1. First Iteration (Compare and Swap)
● Compare the first and second elements starting with the first index.
● The first and second elements are swapped if the first is bigger than the second.
● Compare and contrast the second and third elements now. If they aren't in the right order, swap them.
● The process continues until the last piece is added.
2. Remaining Iteration
For the remaining iterations, the same procedure is followed.
The largest element among the unsorted items is placed at the conclusion of each iteration.
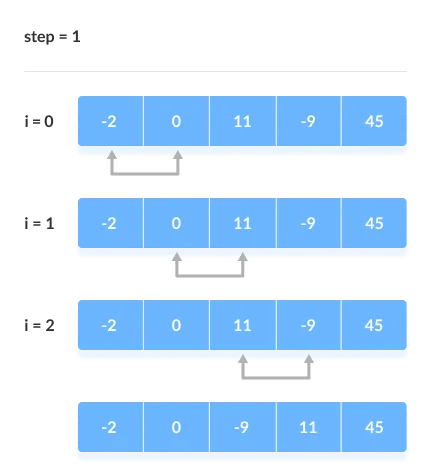
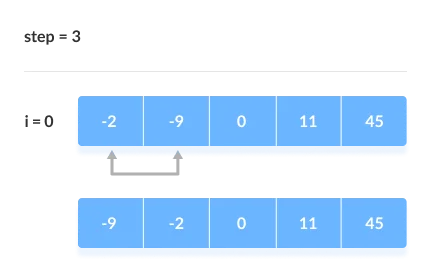
The comparison takes place up to the last unsorted element in each iteration.
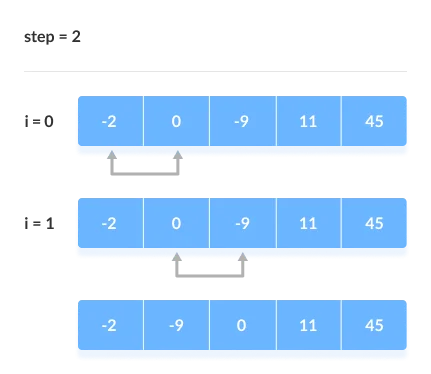
When all of the unsorted elements have been placed in their correct placements, the array is said to be sorted.
Key takeaway
- Compare and swap adjacent elements of the list if they are out of order.
- After repeating the procedure, we end up 'bubbling up' the largest element to the last place on the list by doing it repeatedly.
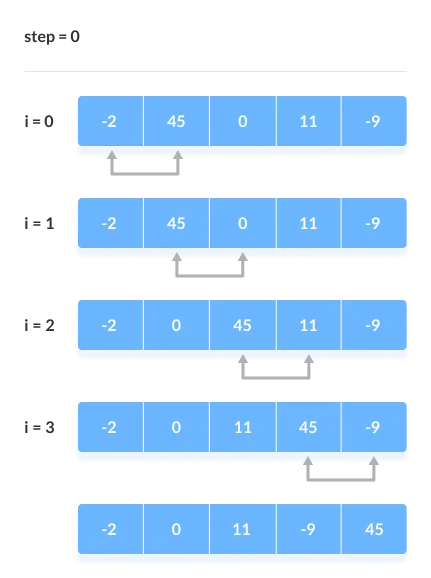
In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
To begin, locate the array's smallest element and set it in the first position. Then locate the array's second smallest element and set it in the second spot. The procedure is repeated till the sorted array is obtained.
The n-1 pass of the selection sort algorithm is used to sort the array of n entries.
● The smallest element of the array, as well as its index pos, must be identified in the first run. Swap A[0] and A[pos] after that. As a result of sorting A[0], we now have n -1 elements to sort.
● The location pos of the smallest element in the sub-array A[n-1] is obtained in the second pas. Swap A[1] and A[pos] after that. After sorting A[0] and A[1], we're left with n-2 unsorted elements.
● The position pos of the smaller element between A[n-1] and A[n-2] must be found in the n-1st pass. Swap A[pos] and A[n-1] after that.
As a result, the items A[0], A[1], A[2],...., A[n-1] are sorted using the procedure described above.
Example
Consider the following six-element array. Using selection sort, sort the array's elements.
A = {10, 2, 3, 90, 43, 56}.
Pass | Pos | A[0] | A[1] | A[2] | A[3] | A[4] | A[5] |
1 | 1 | 2 | 10 | 3 | 90 | 43 | 56 |
2 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
3 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
4 | 4 | 2 | 3 | 10 | 43 | 90 | 56 |
5 | 5 | 2 | 3 | 10 | 43 | 56 | 90 |
Sorted A = {2, 3, 10, 43, 56, 90}
Algorithm
SELECTION SORT(ARR, N)
● Step 1: Repeat Steps 2 and 3 for K = 1 to N-1
● Step 2: CALL SMALLEST(ARR, K, N, POS)
● Step 3: SWAP A[K] with ARR[POS]
[END OF LOOP]
● Step 4: EXIT
SMALLEST (ARR, K, N, POS)
● Step 1: [INITIALIZE] SET SMALL = ARR[K]
● Step 2: [INITIALIZE] SET POS = K
● Step 3: Repeat for J = K+1 to N -1
IF SMALL > ARR[J]
SET SMALL = ARR[J]
SET POS = J
[END OF IF]
[END OF LOOP]
● Step 4: RETURN POS
Key takeaway
- In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
- To begin, locate the array's smallest element and set it in the first position.
- Then locate the array's second smallest element and set it in the second spot.
Insertion style is a decrease & conquer technique application. It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Insertion sorting is a very basic process for sorting numbers in an ascending or descending order. The gradual method is accompanied by this method. It can be contrasted with the method of sorting cards at the time of playing a game.
The numbers that are needed to be sorted are known as keys. Here is the insertion sort method algorithm.
Algorithm:
Algorithm: Insertion-Sort (A)
For j = 2 to A.length
Key = A[j]
// Insert A[j] into the sorted sequence A[1.. j - 1]
i = j - 1
While i > 0 and A[i] > key
A[i + 1] = A[i]
i = i -1
A[i + 1] = key
Analysis:
This algorithm's run time is very dependent on the input given.
If the numbers given are sorted, this algorithm runs in O(n) time. If the numbers given are in reverse order, the algorithm runs in O(n2) time.
Example:
Using insertion sort to sort the following list of elements:
89, 45, 68, 90, 29, 34, 17
89 |45 68 90 29 34 17
45 89 |68 90 29 34 17
45 68 89 |90 29 34 17
45 68 89 90 |29 34 17
29 45 68 89 90 |34 17
29 34 45 68 89 90 |17
17 29 34 45 68 89 90
Application:
In the following instances, the insertion sort algorithm is used:
● When only a few elements are in the list.
● When there are few elements for sorting.
Advantages:
- Straightforward implementation. Three variants exist.
● Left to right scan
● Right to left scan
● Binary insertion sort
2. Effective on a small list of components, on a nearly sorted list.
3. In the best example, running time is linear.
4. This algorithm is stable.
5. Is the on-the-spot algorithm
Key takeaways
- Insertion sorting is a very basic process for sorting numbers in an ascending or descending order.
- Insertion style is a decrease & conquer technique application.
- It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Merge Sort is based on a divide and conquer strategy. It divides the unsorted list into n sublists such that each sublist contains one element. Each sublist is then sorted and merged until there is only one sublist.
Step 1: Divide the list into sublists such that each sublist contains only one element.
Step 2: Sort each sublist and Merge them.
Step 3: Repeat Step 2 till the entire list is sorted.
Example: Apply Merge Sort on array A= {85,24,63,45,17,31,96,50}
Step1: A contains 8 elements. First we divide the list into two sublists such that each sublist contains 4 elements. Then we divide each sublist of 4 elements into sublist of two elements each. Finally every sublist contains only one element.
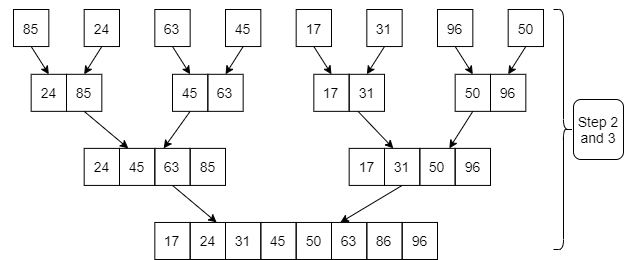
Fig. 3: Example
Step 2: Now we start from the bottom. Compare 1st and 2nd element. Sort and merge them. Apply this for all bottom elements.
Thus we got 4 sublists as follows
24 | 85 |
| 45 | 63 |
| 17 | 31 |
| 50 | 96 |
Step 3: Repeat this sorting and merging until the entire list is sorted. The above four sublists are sorted and merged to form 2 sublists.
24 | 85 | 63 | 85 |
| 17 | 31 | 50 | 96 |
Finally, the above 2 sublists are again sorted and merged in one sublist.
17 | 24 | 31 | 45 | 50 | 63 | 85 | 96 |
We will see one more example on merge sort.
Example: Apply merge Sort on array A={10,5,7,6,1,4,8,3,2,9,12,11}
Step 1:
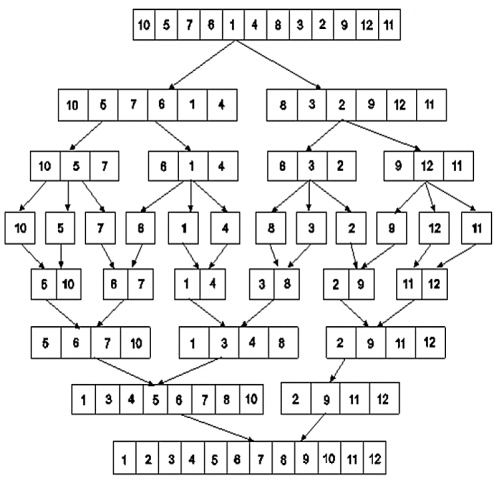
Fig 4: Merge sort
Algorithm for Merge Sort:
Let x = no. Of elements in array A
y = no. Of elements in array B
C = sorted array with no. Of elements n
n = x+y
Following algorithm merges a sorted x element array A and sorted y element array B into a sorted array C, with n = x + y elements. We must always keep track of the locations of the smallest element of A and the smallest element of B which have not yet been placed in C. Let LA and LB denote these locations, respectively. Also, let LC denote the location in C to be filled. Thus, initially, we set
LA: = 1,
LB: = 1 and
LC: = 1.
At each step, we compare A[LA] and B[LB] and assign the smaller element to C[LC].
Then
LC:= LC + 1,
LA: = LA + 1, if a new element has come from A.
LB: = LB + 1, if a new element has come from B.
Furthermore, if LA> x, then the remaining elements of B are assigned to C;
LB >y, then the remaining elements of A are assigned to C.
Thus the algorithm becomes
MERGING ( A, x, B, y, C)
1. [Initialize ] Set LA : = 1 , LB := 1 AND LC : = 1
2. [Compare] Repeat while LA <= x and LB <= y
If A[LA] < B[LB] , then
(a) [Assign element from A to C ] set C[LC] = A[LA]
(b) [Update pointers ] Set LC := LC +1 and LA = LA+1
Else
(a) [Assign element from B to C] Set C[LC] = B[LB]
(b) [Update Pointers] Set LC := LC +1 and LB = LB +1
[End of loop]
3. [Assign remaining elements to C]
If LA > x , then
Repeat for K= 0 ,1,2,........,y–LB
Set C[LC+K] = B[LB+K]
[End of loop]
Else
Repeat for K = 0,1,2,......,x–LA
Set C[LC+K] = A[LA+K]
[End of loop]
4. Exit
Quick sort
Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements. In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions. For this we choose a pivot element and arrange all elements such that all the elements in the left part are less than the pivot and all those in the right part are greater than it.
Algorithm to implement Quick Sort is as follows.
Consider array A of size n to be sorted. p is the pivot element. Index positions of the first and last element of array A are denoted by ‘first’ and ‘last’.
- Initially first=0 and last=n–1.
- Increment first till A[first]<=p
- Decrement last till A[last]>=p
- If first < last then swap A[first] with A[last].
- If first > last then swap p with A[last] and thus the position of p is found. Pivot p is placed such that all elements to its left are less than it and all elements right to it are greater than it. Let us assume that j is the final position of p. Then A[0] to A[j–1] are less than p and A [j + 1] to A [n–1]are greater than p.
- Now we consider the left part of array A i.e A[0] to A[j–1].Repeat step 1,2,3 and 4. Apply the same procedure for the right part of the array.
- We continue with the above steps till no more partitions can be made for every subarray.
Algorithm
PARTITION (ARR, BEG, END, LOC)
● Step 1: [INITIALIZE] SET LEFT = BEG, RIGHT = END, LOC = BEG, FLAG =
● Step 2: Repeat Steps 3 to 6 while FLAG =
● Step 3: Repeat while ARR[LOC] <=ARR[RIGHT]
AND LOC != RIGHT
SET RIGHT = RIGHT - 1
[END OF LOOP]
● Step 4: IF LOC = RIGHT
SET FLAG = 1
ELSE IF ARR[LOC] > ARR[RIGHT]
SWAP ARR[LOC] with ARR[RIGHT]
SET LOC = RIGHT
[END OF IF]
● Step 5: IF FLAG = 0
Repeat while ARR[LOC] >= ARR[LEFT] AND LOC != LEFT
SET LEFT = LEFT + 1
[END OF LOOP]
● Step 6:IF LOC = LEFT
SET FLAG = 1
ELSE IF ARR[LOC] < ARR[LEFT]
SWAP ARR[LOC] with ARR[LEFT]
SET LOC = LEFT
[END OF IF]
[END OF IF]
● Step 7: [END OF LOOP]
● Step 8: END
QUICK_SORT (ARR, BEG, END)
● Step 1: IF (BEG < END)
CALL PARTITION (ARR, BEG, END, LOC)
CALL QUICKSORT(ARR, BEG, LOC - 1)
CALL QUICKSORT(ARR, LOC + 1, END)
[END OF IF]
● Step 2: END
Key takeaways
- Merge sort consisting two phases as divide and merge.
- In divide phase, each time it divides the given unsorted list into two sub list until each sub list get single element then sorts the elements.
- In merge phase, it merges all the solution of sub lists and find the original sorted list.
- Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements.
- In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions.
Counting sort is a stable sorting technique that is used to sort things based on small numbers as keys. It counts the number of keys with the same key value. When the difference between distinct keys isn't too great, this sorting strategy works well; otherwise, it can add to the space complexity.
The counting sort is a sorting method based on the keys that connect certain ranges. Sorting algorithms are frequently asked in coding or technical interviews for software professionals. As a result, it is critical to debate the subject.
This sorting method does not compare elements to sort them. Sorting is accomplished by counting objects with separate key values, similar to hashing. Following that, it does some arithmetic operations to determine the index position of each object in the output sequence. Counting sort isn't commonly used as a sorting algorithm.
When the range of objects to be sorted is not bigger than the number of objects to be sorted, counting sort is effective. It's useful for sorting negative input values.
Algorithm
CountingSort(array, n) // 'n' is the size of array
Max = find maximum element in the given array
Create count array with size maximum + 1
Initialize count array with all 0's
For i = 0 to n
Find the count of every unique element and
Store that count at ith position in the count array
For j = 1 to max
Now, find the cumulative sum and store it in count array
For i = n to 1
Restore the array elements
Decrease the count of every restored element by 1
End countingSort
Working of counting sort Algorithm
Let's have a look at how the counting sort algorithm works.
Let's look at an unsorted array to see how the counting sort algorithm works. An example will make the counting sort easier to comprehend.
Let's say the array's elements are -

1. From the provided array, find the largest element. The maximum element will be max.

2. Create an array with all 0 elements with a length of max + 1. The count of the elements in the specified array will be stored in this array.
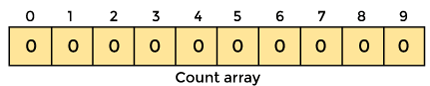
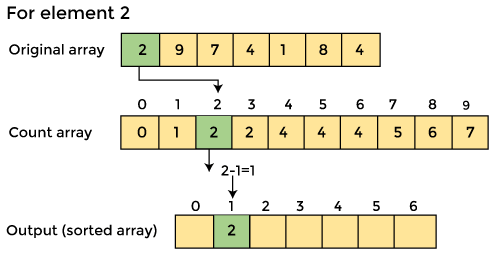
3. Now we must store the count of each array element in the count array at its matching index.
An element's count will be saved as -. Assume that array element '4' appears twice, giving element 4 a count of two. As a result, 2 is placed in the count array's fourth position. If any element is missing from the array, store 0 in its place. For example, if element '3' is missing from the array, 0 will be saved in the third position.


Now save the total sum of the count array entries. It will assist in placing the elements in the sorted array at the correct index.
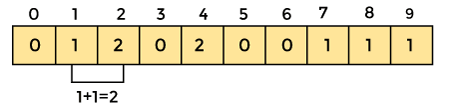
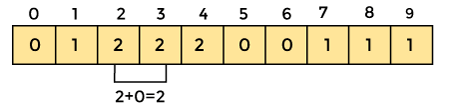
Similarly, the count array's cumulative count is -

4. Now you must determine the index of each element in the original array.
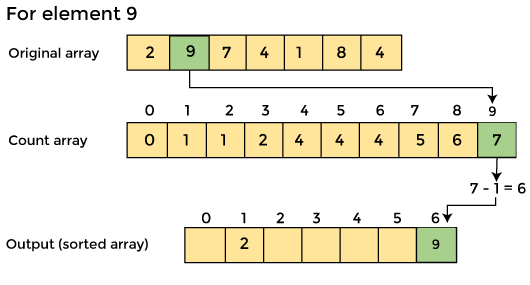
Reduce the element's count by one after it has been placed. Element 2 had a count of 2 before it was placed in the correct position, but now it has a new count of 1.
Key takeaway
Counting sort is a stable sorting technique that is used to sort things based on small numbers as keys.
It counts the number of keys with the same key value.
The counting sort is a sorting method based on the keys that connect certain ranges. Sorting algorithms are frequently asked in coding or technical interviews for software professionals.
The linear search algorithm scans all members of the array iteratively. It takes one second to execute and n seconds to execute, where n is the total number of items in the search array.
It is the simplest data structure search method, and it verifies each item in the set of elements until it matches the searched element until the data collection is complete. A linear search algorithm is favoured over other search algorithms when the data is unsorted.
The following are some of the more difficult aspects of linear search:
Space complexity
Because linear search takes up no more space, it has an O(n) space complexity, where n is the number of entries in an array.
Time complexity
● When the searched item is present at the first entry in the search array, the best-case complexity = O(1) occurs.
● When the necessary element is at the end of the array or not present at all, worst-case complexity = O(n) occurs.
● When the object to be searched is in the middle of the Array, the average-case complexity = average case happens.
Procedure for linear search
Procedure linear_search (list, value)
For each item in the list
If match item == value
Return the item's location
End if
End for
End procedure
Binary search
By comparing the data collection's middlemost pieces, this technique locates specific things. When a match is detected, the item's index is returned. It looks for a center item of the left sub-array when the middle item is greater than the search item. If the middle item, on the other hand, is smaller than the search item, it looks for it in the right sub-array. It continues to hunt for an item until it finds it or the sub-array size approaches zero.
The array's items must be sorted in order for binary search to work. It outperforms a linear search algorithm in terms of speed. The divide and conquer technique is used in the binary search.
Run-time complexity = O(log n)
Complexities in binary search are given below:
● The worst-case complexity in binary search is O(n log n).
● The average case complexity in binary search is O(n log n)
● Best case complexity = O (1)
Binary search algorithm
Procedure binary_search
A ← sorted array
n ← size of array
x ← value to be searched
Set lowerBound = 1
Set upperBound = n
While x not found
If upperBound < lowerBound
EXIT: x does not exists.
Set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
If A[midPoint] x
Set upperBound = midPoint - 1
If A[midPoint] = x
EXIT: x found at location midPoint
End while
End procedure
Key takeaway
The linear search algorithm scans all members of the array iteratively.
It takes one second to execute and n seconds to execute, where n is the total number of items in the search array.
By comparing the data collection's middlemost pieces, this technique locates specific things.
When a match is detected, the item's index is returned.
References:
- Data Structures Using C – A.M. Tenenbaum (PHI)
- Introduction to Data Structures with Applications by J. Tremblay and P. G. Sorenson (TMH)
- Data Structure and Program Design in C by C.L. Tondo.
- Data Structures and Algorithms in C, M.T. Goodrich, R. Tamassia and D. Mount, Wiley, India.
- Data Structure Using C by Pankaj Kumar Pandey.
- Data Structure with C, Tata McGraw Hill Education Private Limited by Seymour Lipschutz.
- Https://opendatastructures.org/ods-cpp/1_3_Mathematical_Background.html
Unit - 1
Basic concepts and notations
A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively. Arrays, Linked Lists, Stacks, Queues, and other Data Structures are examples. Data Structures are employed in practically every element of computer science, including operating systems, compiler design, artificial intelligence, graphics, and many more applications.
Data Structures are an important aspect of many computer science algorithms because they allow programmers to efficiently handle data. It is critical to improving the performance of a software or program because the software's primary duty is to save and retrieve user data as quickly as feasible.
Basic terminology
The building blocks of every program or software are data structures. The most challenging challenge for a programmer is deciding on a suitable data structure for a program. When it comes to data structures, the following terminology is utilized.
Data: The data on a student can be defined as an elementary value or a set of values, for example, the student's name and id.
Group items: Group items are data items that include subordinate data items, such as a student's name, which can have both a first and a last name.
Record: A record can be characterized as a collection of several data objects. For example, if we consider the student entity, the name, address, course, and grades can all be gathered together to constitute the student's record.
File: A file is a collection of various records of one type of entity; for example, if there are 60 employees in the class, the relevant file will contain 20 records, each containing information about each employee.
Attribute and Entity: A class of objects is represented by an entity. It has a number of characteristics. Each attribute represents an entity's specific property.
Operations
- Traversing
The set of data elements is present in every data structure. Traversing a data structure is going through each element in order to perform a certain action, such as searching or sorting.
For example, if we need to discover the average of a student's grades in six different topics, we must first traverse the entire array of grades and calculate the total amount, then divide that sum by the number of subjects, which in this case is six, to find the average.
2. Insertion
The process of adding elements to the data structure at any position is known as insertion.
We can only introduce n-1 data elements into a data structure if its size is n.
3. Deletion
Deletion is the process of eliminating an element from a data structure. We can remove an element from the data structure at any point in the data structure.
Underflow occurs when we try to delete an element from an empty data structure.
4. Searching
Searching is the process of discovering an element's location within a data structure. There are two types of search algorithms: Linear Search and Binary Search.
5. Sorting
Sorting is the process of putting the data structure in a specified order. Sorting can be done using a variety of algorithms, such as insertion sort, selection sort, bubble sort, and so on.
6. Merging
Merging occurs when two lists, List A and List B, of size M and N, respectively, containing comparable types of elements are combined to form a third list, List C, of size (M+N).
Key takeaway
A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively.
Arrays, Linked Lists, Stacks, Queues, and other Data Structures are examples.
Data Structures are an important aspect of many computer science algorithms because they allow programmers to efficiently handle data.
We will go through some of the mathematical notations and tools that will be used throughout the book, such as logarithms, big-Oh notation, and probability theory.
Exponentials and Logarithms
The number $ b$ raised to the power of x is denoted by the expression bx. If $ x$ is a positive integer, the value of b multiplied by itself x-1 times is:
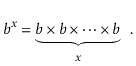
bx =1/b-x when x is a negative integer. When x equals 0, bx =1. When b is not an integer, exponentiation can still be expressed in terms of the exponential function ex, which is defined in terms of the exponential series, although this is best left to a calculus textbook.
The base- b logarithm of k is denoted by the phrase logb k. That is, the one and only x value that fulfills.
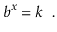
The base 2 logarithms make up the majority of the logarithms in this book (binary logarithms). We ignore the base for these, thus log k is shorthand for log2 k.
Think of logb k as the number of times we have to divide k by b before the result is less than or equal to 1. This is an informal but effective method of thinking about logarithms. When using binary search, for example, each comparison reduces the number of possible solutions by a factor of two. This process is continued until only one possible response remains. When there are at most n+1 potential responses, the number of comparisons performed using binary search is at most [log2 (n+1)].
The natural logarithm is another logarithm that appears multiple times. To express loge k, we use the notation ln k, where e, Euler's constant, is provided by
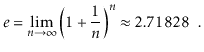
The natural logarithm is commonly mentioned because it is the value of a widely used integral:
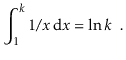
Removing logarithms from an exponent is one of the most common operations using them:
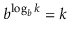
And modifying a logarithm's base:
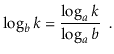
These two modifications, for example, can be used to compare natural and binary logarithms.
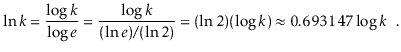
Asymptotic notations
When we look at data structures in this book, we'll talk about how long various operations take. Of course, the exact running timings will vary from computer to computer and even from run to run on a same computer. When we talk about an operation's running time, we're talking to the number of computer instructions executed during that period. Even with basic code, calculating this figure precisely can be tricky. As a result, rather than examining running times precisely, we'll employ the so-called big-Oh notation: O(f(n)) denotes a set of functions for a function f(n).
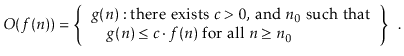
This collection comprises functions g(n) where c. f(n) begins to dominate g(n) when n is large enough.
To simplify functions, we usually employ asymptotic notation. For example, we can write O(nlog n) instead of 5n log n + 8n - 200. This is demonstrated as follows:
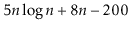
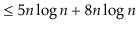
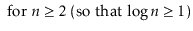
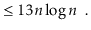
Using the constants c=13 and n 0 = 2, this shows that the function f(n)=5nlog n + 8n - 200 is in the set O(nlog n).
Big-Oh notation isn't new or exclusive to the field of computer science. It was first used in 1894 by number theorist Paul Bachmann, and it is extremely valuable for defining the execution periods of computer algorithms. Take a look at the following code:
Void snippet() {
For (int i = 0; i < n; i++)
a[i] = i;
}
One execution of this method involves
● 1 assignment ( int i = 0 ),
● n +1 comparisons ( i < n ),
● n increments ( i ++ ),
● n array offset calculations ( a [i] ), and
● n indirect assignments ( a [i] = i ).
As a result, this running time may be written as
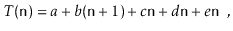
Where a, b, c, d, and e are machine-dependent constants that indicate the time it takes to conduct assignments, comparisons, increment operations, array offset calculations, and indirect assignments, respectively. If, on the other hand, this expression represents the execution time of two lines of code, then this type of analysis will clearly be unsuitable for complex code or algorithms. The running time can be simplified to using big-Oh notation.
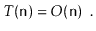
This is not only more compact, but it also provides roughly the same amount of information. Because the running time in the previous example is dependent on the constants a, b, c, d, and e, it will be impossible to compare two running times to see which is quicker without knowing the values of these constants. Even if we put forth the effort to identify these constants (for example, through timing tests), our conclusion will be valid only for the system on which we conducted our tests.
Big-Oh notation enables us to reason at a much higher level, allowing us to examine more complex functions. We won't know which algorithm is faster if both have the same big-Oh running time, and there may not be a clear winner. One might be faster on one machine, while the other might be quicker on another. If the two algorithms have measurably different big-Oh running times, we can be confident that the one with the shorter running time will be faster for large enough n values.
Factorial
The product of the positive numbers 1 to n is denoted by n!. n! stands for 'n factorial,' i.e.
n! = 1 * 2 * 3 * ….. * (n-2) * (n-1) * n
Example
4! = 1 * 2 * 3 * 4 = 24
5! = 5 * 4! = 120
Randomization and Probability
Some of the data structures described in this book are randomized; they make random decisions regardless of the data they contain or the operations they execute. As a result, doing the same set of actions with these structures multiple times may result in varying running times. We're interested in the average or expected execution times of these data structures when we examine them.
We wish to investigate the predicted value of the running time of an operation on a randomized data structure, which is a random variable. The expected value of a discrete random variable X taking on values in some countable universe U is given by the formula E[X].
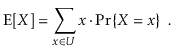
The probability that the event E occurs is denoted by PrE. These probabilities are solely applied to the randomized data structure's random selections in this book; there is no assumption that the data contained in the structure, or the sequence of operations done on the data structure, is random.
The linearity of expectation is one of the most essential features of expected values. If X and Y are two random variables,
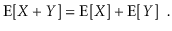
More generally, for any random variables X1,........,Xk,
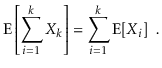
We can break down sophisticated random variables (such the left hand sides of the preceding equations) into sums of smaller random variables thanks to linearity of expectation (the right hand sides).
If we consider X to be an algorithm and N to be the size of the input data, the time and space implemented by Algorithm X are the two key criteria that determine X's efficiency.
Time Factor - The time is determined or assessed by measuring the number of critical operations in the sorting algorithm, such as comparisons.
Space Factor - The space is estimated or measured by counting the algorithm's maximum memory requirements.
With respect to N as the size of input data, the complexity of an algorithm f(N) provides the running time and/or storage space required by the method.
Space complexity
The amount of memory space required by an algorithm during its life cycle is referred to as its space complexity.
The sum of the following two components represents the amount of space required by an algorithm.
A fixed component is a space needed to hold specific data and variables (such as simple variables and constants, program size, and so on) that are independent of the problem's size.
A variable part is a space that variables require and whose size is entirely dependent on the problem's magnitude. Recursion stack space, dynamic memory allocation, and so forth.
Complexity of space Any algorithm p's S(p) is S(p) = A + Sp (I) Where A is the fixed component of the algorithm and S(I) is the variable part of the algorithm that is dependent on the instance characteristic I. Here's a basic example to help you understand the concept.
Algorithm
SUM(P, Q)
Step 1 - START
Step 2 - R ← P + Q + 10
Step 3 - Stop
There are three variables here: P, Q, and R, as well as one constant. As a result, S(p) = 1+3. Now, the amount of space available is determined by the data types of specified constant types and variables, and it is multiplied accordingly.
Time complexity
The time complexity of an algorithm is a representation of how long it takes for the algorithm to complete its execution. Time requirements can be expressed or specified as a numerical function t(N), where N is the number of steps and t(N) is the time taken by each step.
When adding two n-bit numbers, for example, N steps are taken. As a result, the total processing time is t(N) = c*n, where c represents the time spent adding two bits. We can see that as the input size grows, t(N) climbs linearly.
Time space trade off
- It is also known as time memory tradeoff.
- It is a way of solving problems in less time by using more storage space.
- It can be used with the problem of data storage.
- For example: time complexity of merge sort is O(n log n)in all cases. But requires an auxiliary array.
- In quick sort complexity is O(n log n) for best and average case but it doesn’t require auxiliary space.
- Two Space-for-Time Algorithm Varieties:
- Input enhancement - To store some info, preprocess the input (or its portion) to be used in solving the issue later
- Counting sorts
- String searching algorithms
- Pre-structuring-preprocessing the input to access its components
1) hashing 2) indexing schemes simpler (e.g., B-trees)
Big Oh (O) Notation:
- It is the formal way to express the time complexity.
- It is used to define the upper bound of an algorithm’s running time.
- It shows the worst-case time complexity or largest amount of time taken by the algorithm to perform a certain task.
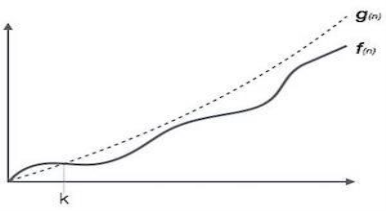
Fig 1: Big Oh notation
Here, f (n) <= g (n) …………….(eq1)
Where n>= k, C>0 and k>=1
If any algorithm satisfies the eq1 condition then it becomes f (n)= O (g (n))
Properties of Big oh notation
The definition of big O is pretty ugly to have to work with all the time, kind of like the "limit" definition of a derivative in Calculus. Here are some helpful theorems you can use to simplify big O calculations:
● Any kth degree polynomial is O(nk).
● a nk = O(nk) for any a > 0.
● Big O is transitive. That is, if f(n) = O(g(n)) and g(n) is O(h(n)), then f(n) = O(h(n)).
● logan = O(logb n) for any a, b > 1. This practically means that we don't care, asymptotically, what base we take our logarithms to. (I said asymptotically. In a few cases, it does matter.)
● Big O of a sum of functions is big O of the largest function. How do you know which one is the largest? The one that all the others are big O of. One consequence of this is, if f(n) = O(h(n)) and g(n) is O(h(n)), then f(n) + g(n) = O(h(n)).
● f(n) = O(g(n)) is true if limn->infinity f(n)/g(n) is a constant.
Key takeaway
- It is also known as a time memory tradeoff.
- It is a way of solving problems in less time by using more storage space.
We all know that as the input size (n) grows, the running time of an algorithm grows (or stays constant in the case of constant running time). Even if the input has the same size, the running duration differs between distinct instances of the input. In this situation, we examine the best, average, and worst-case scenarios. The best case running time is the shortest, the worst case running time is the longest, and the average case running time is the time required to execute the algorithm on average. All of these principles will be explained using two examples: I linear search and (ii) insertion sort.
Best case
Consider the case of Linear Search, in which we look for a certain item in an array. We return the relevant index if the item is in the array; else, we return -1. The linear search code is provided below.
Int search(int a, int n, int item) {
Int i;
For (i = 0; i < n; i++) {
If (a[i] == item) {
Return a[i]
}
}
Return -1
}
Variable an is an array, n is the array's size, and item is the array item we're looking for. It will return the index immediately if the item we're seeking for is in the very first position of the array. The for loop is just executed once. In this scenario, the complexity will be O. (1). This is referred to be the best case scenario.
Average case
On occasion, we perform an average case analysis on algorithms. The average case is nearly as severe as the worst scenario most of the time. When attempting to insert a new item into its proper location using insertion sort, we compare the new item to half of the sorted items on average. The complexity remains on the order of n2, which corresponds to the worst-case running time.
Analyzing an algorithm's average behavior is usually more difficult than analyzing its worst-case behavior. This is due to the fact that it is not always clear what defines a "average" input for a given situation. As a result, a useful examination of an algorithm's average behavior necessitates previous knowledge of the distribution of input instances, which is an impossible condition. As a result, we frequently make the assumption that all inputs of a given size are equally likely and do the probabilistic analysis for the average case.
Worst case
In real life, we almost always perform a worst-case analysis on an algorithm. The longest running time for any input of size n is called the worst case running time.
The worst case scenario in a linear search is when the item we're looking for is at the last place of the array or isn't in the array at all. We must run through all n elements in the array in both circumstances. As a result, the worst-case runtime is O. (n). In the case of linear search, worst-case performance is more essential than best-case performance for the following reasons.
● Rarely is the object we're looking for in the first position. If there are 1000 entries in the array, start at 1 and work your way up. There is a 0.001% probability that the item will be in the first place if we search it at random from 1 to 1000.
● Typically, the item isn't in the array (or database in general). In that situation, the worst-case running time is used.
Similarly, when items are reverse sorted in insertion sort, the worst case scenario occurs. In the worst scenario, the number of comparisons will be on the order of n2, and hence the running time will be O (n2).
Knowing an algorithm's worst-case performance ensures that the algorithm will never take any longer than it does today.
Key takeaway
The best case running time is the shortest, the worst case running time is the longest, and the average case running time is the time required to execute the algorithm on average.
An array is a collection of data items, all of the same type, accessed using a common name.
A one-dimensional array is like a list; A two dimensional array is like a table; The C language places no limits on the number of dimensions in an array, though specific implementations may.
Some texts refer to one-dimensional arrays as vectors, two-dimensional arrays as matrices, and use the general term arrays when the number of dimensions is unspecified or unimportant.
Linear arrays
A one-dimensional array, often known as a single-dimensional array, is one in which a single subscript specification is required to identify a specific array element. We can declare a one-dimensional array as follows:
Data_type array_name [Expression];
Where,
Data_type - The kind of element to be stored in the array is data type.
Array_name - array name specifies the array's name; it can be any type of name, much like other simple variables.
Expression - The number of values to be placed in the array is supplied; arrays are sometimes known as subscripted values; the subscript value must be an integer value, therefore the array's subscript begins at 0.
Example:
Int "a" [10]
Where int: data type
a: array name
10: expression
Output
Data values are dummy values, you can understand after seeing the output, indexing starts from “0”.
Multidimensional Arrays
A 2D array can be defined as an array of arrays. The 2D array is organized as matrices which can be represented as the collection of rows and columns.
However, 2D arrays are created to implement a relational database look alike data structure. It provides ease of holding bulk data at once which can be passed to any number of functions wherever required.
How to declare 2D Array
The syntax of declaring a two dimensional array is very much similar to that of a one dimensional array, given as follows.
Int arr[max_rows][max_columns];
However, It produces the data structure which looks like the following.
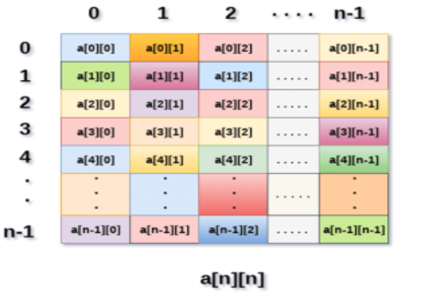
Fig 2: Example
Above image shows the two dimensional array, the elements are organized in the form of rows and columns. First element of the first row is represented by a[0][0] where the number shown in the first index is the number of that row while the number shown in the second index is the number of the column.
How do we access data in a 2D array
Due to the fact that the elements of 2D arrays can be random accessed. Similar to one dimensional arrays, we can access the individual cells in a 2D array by using the indices of the cells. There are two indices attached to a particular cell, one is its row number while the other is its column number.
However, we can store the value stored in any particular cell of a 2D array to some variable x by using the following syntax.
Int x = a[i][j];
Where i and j is the row and column number of the cell respectively.
We can assign each cell of a 2D array to 0 by using the following code:
- For ( int i=0; i<n ;i++)
- {
- For (int j=0; j<n; j++)
- {
- a[i][j] = 0;
- }
- }
Initializing 2D Arrays
We know that, when we declare and initialize a one dimensional array in C programming simultaneously, we don't need to specify the size of the array. However this will not work with 2D arrays. We will have to define at least the second dimension of the array.
The syntax to declare and initialize the 2D array is given as follows.
Int arr[2][2] = {0,1,2,3};
The number of elements that can be present in a 2D array will always be equal to (number of rows * number of columns).
Example: Storing User's data into a 2D array and printing it.
C Example:
- #include <stdio.h>
- Void main ()
- {
- Int arr[3][3],i,j;
- For (i=0;i<3;i++)
- {
- For (j=0;j<3;j++)
- {
- Printf("Enter a[%d][%d]: ",i,j);
- Scanf("%d",&arr[i][j]);
- }
- }
- Printf("\n printing the elements ....\n");
- For(i=0;i<3;i++)
- {
- Printf("\n");
- For (j=0;j<3;j++)
- {
- Printf("%d\t",arr[i][j]);
- }
- }
- }
Key takeaway
An array is a collection of data items, all of the same type, accessed using a common name.
A one-dimensional array is like a list; A two dimensional array is like a table; The C language places no limits on the number of dimensions in an array, though specific implementations may.
Arrays can be declared in a variety of ways depending on the language.

Arrays can be declared in a variety of ways depending on the language. Consider the C array declaration as an example.

The following are the key points to consider, as shown in the diagram above.
● The index begins with a zero.
● The length of the array is 10, which indicates it can hold ten elements.
● The index of each element can be used to access it. For example, an element at index 6 can be retrieved as 9.
Traversal
The traversal of an array's elements is performed with this operation.
Example
The following software walks an array and outputs its elements:
#include <stdio.h>
Main() {
Int LA[] = {1,3,5,7,8};
Int item = 10, k = 3, n = 5;
Int i = 0, j = n;
Printf("The original array elements are :\n");
For(i = 0; i<n; i++) {
Printf("LA[%d] = %d \n", i, LA[i]);
}
}
When we compile and run the preceding program, we get the following result:
Output
The original array elements are:
LA[0] = 1
LA[1] = 3
LA[2] = 5
LA[3] = 7
LA[4] = 8
Bubble Sort is a simple algorithm for sorting a collection of n elements that is provided in the form of an array with n elements. Bubble Sort compares each element individually and sorts them according to their values.
If an array must be sorted in ascending order, bubble sort will begin by comparing the first and second members of the array, swapping both elements if the first element is greater than the second, and then moving on to compare the second and third elements, and so on.
If there are n elements in total, we must repeat the method n-1 times.
It's called bubble sort because the largest element in the given array bubbles up to the last position or highest index with each full iteration, similar to how a water bubble rises to the sea surface.
Although it is simple to use, bubble sort is largely employed as an educational tool because its performance in the actual world is low. It isn't designed to handle huge data collections. Bubble sort has an average and worst-case complexity of O(n2), where n is the number of elements.
Sorting is done by going through all of the items one by one, comparing them to the next closest element, and swapping them if necessary.
Algorithm
Assume arr is an array of n elements in the algorithm below. The algorithm's presumed swap function will swap the values of specified array members.
Begin BubbleSort(arr)
For all array elements
If arr[i] > arr[i+1]
Swap(arr[i], arr[i+1])
End if
End for
Return arr
End BubbleSort
Working of Bubble Sort
Assume we're attempting to arrange the elements in ascending order.
1. First Iteration (Compare and Swap)
● Compare the first and second elements starting with the first index.
● The first and second elements are swapped if the first is bigger than the second.
● Compare and contrast the second and third elements now. If they aren't in the right order, swap them.
● The process continues until the last piece is added.
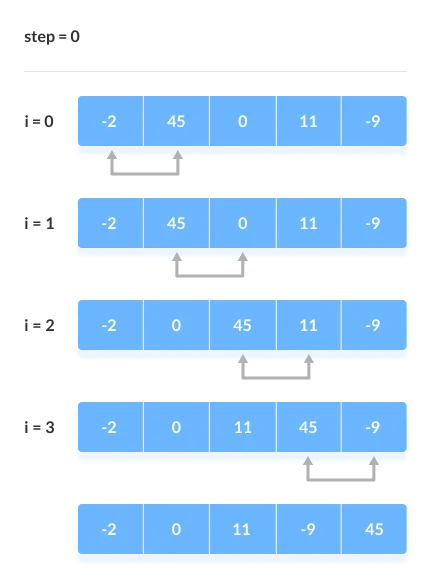
2. Remaining Iteration
For the remaining iterations, the same procedure is followed.
The largest element among the unsorted items is placed at the conclusion of each iteration.
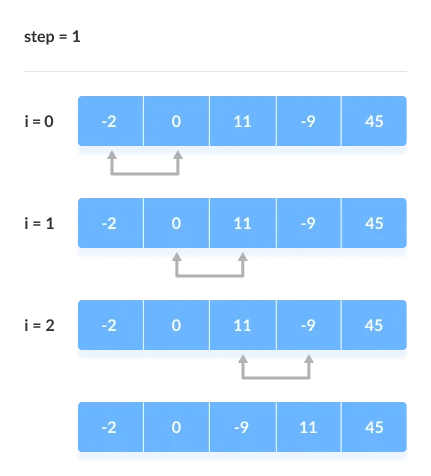
The comparison takes place up to the last unsorted element in each iteration.
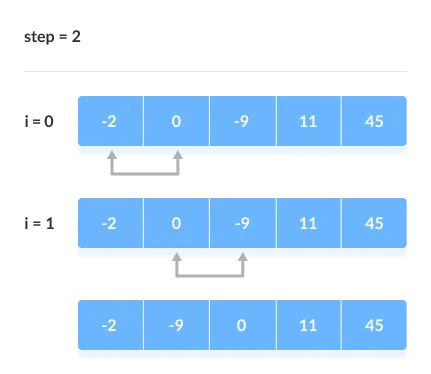
When all of the unsorted elements have been placed in their correct placements, the array is said to be sorted.
Key takeaway
- Compare and swap adjacent elements of the list if they are out of order.
- After repeating the procedure, we end up 'bubbling up' the largest element to the last place on the list by doing it repeatedly.
In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
To begin, locate the array's smallest element and set it in the first position. Then locate the array's second smallest element and set it in the second spot. The procedure is repeated till the sorted array is obtained.
The n-1 pass of the selection sort algorithm is used to sort the array of n entries.
● The smallest element of the array, as well as its index pos, must be identified in the first run. Swap A[0] and A[pos] after that. As a result of sorting A[0], we now have n -1 elements to sort.
● The location pos of the smallest element in the sub-array A[n-1] is obtained in the second pas. Swap A[1] and A[pos] after that. After sorting A[0] and A[1], we're left with n-2 unsorted elements.
● The position pos of the smaller element between A[n-1] and A[n-2] must be found in the n-1st pass. Swap A[pos] and A[n-1] after that.
As a result, the items A[0], A[1], A[2],...., A[n-1] are sorted using the procedure described above.
Example
Consider the following six-element array. Using selection sort, sort the array's elements.
A = {10, 2, 3, 90, 43, 56}.
Pass | Pos | A[0] | A[1] | A[2] | A[3] | A[4] | A[5] |
1 | 1 | 2 | 10 | 3 | 90 | 43 | 56 |
2 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
3 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
4 | 4 | 2 | 3 | 10 | 43 | 90 | 56 |
5 | 5 | 2 | 3 | 10 | 43 | 56 | 90 |
Sorted A = {2, 3, 10, 43, 56, 90}
Algorithm
SELECTION SORT(ARR, N)
● Step 1: Repeat Steps 2 and 3 for K = 1 to N-1
● Step 2: CALL SMALLEST(ARR, K, N, POS)
● Step 3: SWAP A[K] with ARR[POS]
[END OF LOOP]
● Step 4: EXIT
SMALLEST (ARR, K, N, POS)
● Step 1: [INITIALIZE] SET SMALL = ARR[K]
● Step 2: [INITIALIZE] SET POS = K
● Step 3: Repeat for J = K+1 to N -1
IF SMALL > ARR[J]
SET SMALL = ARR[J]
SET POS = J
[END OF IF]
[END OF LOOP]
● Step 4: RETURN POS
Key takeaway
- In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
- To begin, locate the array's smallest element and set it in the first position.
- Then locate the array's second smallest element and set it in the second spot.
Insertion style is a decrease & conquer technique application. It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Insertion sorting is a very basic process for sorting numbers in an ascending or descending order. The gradual method is accompanied by this method. It can be contrasted with the method of sorting cards at the time of playing a game.
The numbers that are needed to be sorted are known as keys. Here is the insertion sort method algorithm.
Algorithm:
Algorithm: Insertion-Sort (A)
For j = 2 to A.length
Key = A[j]
// Insert A[j] into the sorted sequence A[1.. j - 1]
i = j - 1
While i > 0 and A[i] > key
A[i + 1] = A[i]
i = i -1
A[i + 1] = key
Analysis:
This algorithm's run time is very dependent on the input given.
If the numbers given are sorted, this algorithm runs in O(n) time. If the numbers given are in reverse order, the algorithm runs in O(n2) time.
Example:
Using insertion sort to sort the following list of elements:
89, 45, 68, 90, 29, 34, 17
89 |45 68 90 29 34 17
45 89 |68 90 29 34 17
45 68 89 |90 29 34 17
45 68 89 90 |29 34 17
29 45 68 89 90 |34 17
29 34 45 68 89 90 |17
17 29 34 45 68 89 90
Application:
In the following instances, the insertion sort algorithm is used:
● When only a few elements are in the list.
● When there are few elements for sorting.
Advantages:
- Straightforward implementation. Three variants exist.
● Left to right scan
● Right to left scan
● Binary insertion sort
2. Effective on a small list of components, on a nearly sorted list.
3. In the best example, running time is linear.
4. This algorithm is stable.
5. Is the on-the-spot algorithm
Key takeaways
- Insertion sorting is a very basic process for sorting numbers in an ascending or descending order.
- Insertion style is a decrease & conquer technique application.
- It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Merge Sort is based on a divide and conquer strategy. It divides the unsorted list into n sublists such that each sublist contains one element. Each sublist is then sorted and merged until there is only one sublist.
Step 1: Divide the list into sublists such that each sublist contains only one element.
Step 2: Sort each sublist and Merge them.
Step 3: Repeat Step 2 till the entire list is sorted.
Example: Apply Merge Sort on array A= {85,24,63,45,17,31,96,50}
Step1: A contains 8 elements. First we divide the list into two sublists such that each sublist contains 4 elements. Then we divide each sublist of 4 elements into sublist of two elements each. Finally every sublist contains only one element.
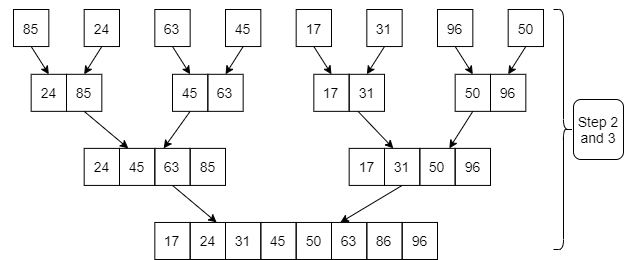
Fig. 3: Example
Step 2: Now we start from the bottom. Compare 1st and 2nd element. Sort and merge them. Apply this for all bottom elements.
Thus we got 4 sublists as follows
24 | 85 |
| 45 | 63 |
| 17 | 31 |
| 50 | 96 |
Step 3: Repeat this sorting and merging until the entire list is sorted. The above four sublists are sorted and merged to form 2 sublists.
24 | 85 | 63 | 85 |
| 17 | 31 | 50 | 96 |
Finally, the above 2 sublists are again sorted and merged in one sublist.
17 | 24 | 31 | 45 | 50 | 63 | 85 | 96 |
We will see one more example on merge sort.
Example: Apply merge Sort on array A={10,5,7,6,1,4,8,3,2,9,12,11}
Step 1:
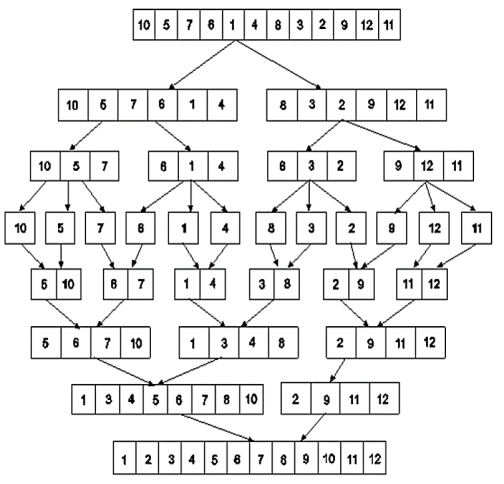
Fig 4: Merge sort
Algorithm for Merge Sort:
Let x = no. Of elements in array A
y = no. Of elements in array B
C = sorted array with no. Of elements n
n = x+y
Following algorithm merges a sorted x element array A and sorted y element array B into a sorted array C, with n = x + y elements. We must always keep track of the locations of the smallest element of A and the smallest element of B which have not yet been placed in C. Let LA and LB denote these locations, respectively. Also, let LC denote the location in C to be filled. Thus, initially, we set
LA: = 1,
LB: = 1 and
LC: = 1.
At each step, we compare A[LA] and B[LB] and assign the smaller element to C[LC].
Then
LC:= LC + 1,
LA: = LA + 1, if a new element has come from A.
LB: = LB + 1, if a new element has come from B.
Furthermore, if LA> x, then the remaining elements of B are assigned to C;
LB >y, then the remaining elements of A are assigned to C.
Thus the algorithm becomes
MERGING ( A, x, B, y, C)
1. [Initialize ] Set LA : = 1 , LB := 1 AND LC : = 1
2. [Compare] Repeat while LA <= x and LB <= y
If A[LA] < B[LB] , then
(a) [Assign element from A to C ] set C[LC] = A[LA]
(b) [Update pointers ] Set LC := LC +1 and LA = LA+1
Else
(a) [Assign element from B to C] Set C[LC] = B[LB]
(b) [Update Pointers] Set LC := LC +1 and LB = LB +1
[End of loop]
3. [Assign remaining elements to C]
If LA > x , then
Repeat for K= 0 ,1,2,........,y–LB
Set C[LC+K] = B[LB+K]
[End of loop]
Else
Repeat for K = 0,1,2,......,x–LA
Set C[LC+K] = A[LA+K]
[End of loop]
4. Exit
Quick sort
Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements. In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions. For this we choose a pivot element and arrange all elements such that all the elements in the left part are less than the pivot and all those in the right part are greater than it.
Algorithm to implement Quick Sort is as follows.
Consider array A of size n to be sorted. p is the pivot element. Index positions of the first and last element of array A are denoted by ‘first’ and ‘last’.
- Initially first=0 and last=n–1.
- Increment first till A[first]<=p
- Decrement last till A[last]>=p
- If first < last then swap A[first] with A[last].
- If first > last then swap p with A[last] and thus the position of p is found. Pivot p is placed such that all elements to its left are less than it and all elements right to it are greater than it. Let us assume that j is the final position of p. Then A[0] to A[j–1] are less than p and A [j + 1] to A [n–1]are greater than p.
- Now we consider the left part of array A i.e A[0] to A[j–1].Repeat step 1,2,3 and 4. Apply the same procedure for the right part of the array.
- We continue with the above steps till no more partitions can be made for every subarray.
Algorithm
PARTITION (ARR, BEG, END, LOC)
● Step 1: [INITIALIZE] SET LEFT = BEG, RIGHT = END, LOC = BEG, FLAG =
● Step 2: Repeat Steps 3 to 6 while FLAG =
● Step 3: Repeat while ARR[LOC] <=ARR[RIGHT]
AND LOC != RIGHT
SET RIGHT = RIGHT - 1
[END OF LOOP]
● Step 4: IF LOC = RIGHT
SET FLAG = 1
ELSE IF ARR[LOC] > ARR[RIGHT]
SWAP ARR[LOC] with ARR[RIGHT]
SET LOC = RIGHT
[END OF IF]
● Step 5: IF FLAG = 0
Repeat while ARR[LOC] >= ARR[LEFT] AND LOC != LEFT
SET LEFT = LEFT + 1
[END OF LOOP]
● Step 6:IF LOC = LEFT
SET FLAG = 1
ELSE IF ARR[LOC] < ARR[LEFT]
SWAP ARR[LOC] with ARR[LEFT]
SET LOC = LEFT
[END OF IF]
[END OF IF]
● Step 7: [END OF LOOP]
● Step 8: END
QUICK_SORT (ARR, BEG, END)
● Step 1: IF (BEG < END)
CALL PARTITION (ARR, BEG, END, LOC)
CALL QUICKSORT(ARR, BEG, LOC - 1)
CALL QUICKSORT(ARR, LOC + 1, END)
[END OF IF]
● Step 2: END
Key takeaways
- Merge sort consisting two phases as divide and merge.
- In divide phase, each time it divides the given unsorted list into two sub list until each sub list get single element then sorts the elements.
- In merge phase, it merges all the solution of sub lists and find the original sorted list.
- Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements.
- In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions.
Counting sort is a stable sorting technique that is used to sort things based on small numbers as keys. It counts the number of keys with the same key value. When the difference between distinct keys isn't too great, this sorting strategy works well; otherwise, it can add to the space complexity.
The counting sort is a sorting method based on the keys that connect certain ranges. Sorting algorithms are frequently asked in coding or technical interviews for software professionals. As a result, it is critical to debate the subject.
This sorting method does not compare elements to sort them. Sorting is accomplished by counting objects with separate key values, similar to hashing. Following that, it does some arithmetic operations to determine the index position of each object in the output sequence. Counting sort isn't commonly used as a sorting algorithm.
When the range of objects to be sorted is not bigger than the number of objects to be sorted, counting sort is effective. It's useful for sorting negative input values.
Algorithm
CountingSort(array, n) // 'n' is the size of array
Max = find maximum element in the given array
Create count array with size maximum + 1
Initialize count array with all 0's
For i = 0 to n
Find the count of every unique element and
Store that count at ith position in the count array
For j = 1 to max
Now, find the cumulative sum and store it in count array
For i = n to 1
Restore the array elements
Decrease the count of every restored element by 1
End countingSort
Working of counting sort Algorithm
Let's have a look at how the counting sort algorithm works.
Let's look at an unsorted array to see how the counting sort algorithm works. An example will make the counting sort easier to comprehend.
Let's say the array's elements are -

1. From the provided array, find the largest element. The maximum element will be max.

2. Create an array with all 0 elements with a length of max + 1. The count of the elements in the specified array will be stored in this array.
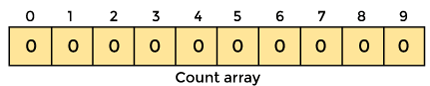
3. Now we must store the count of each array element in the count array at its matching index.
An element's count will be saved as -. Assume that array element '4' appears twice, giving element 4 a count of two. As a result, 2 is placed in the count array's fourth position. If any element is missing from the array, store 0 in its place. For example, if element '3' is missing from the array, 0 will be saved in the third position.


Now save the total sum of the count array entries. It will assist in placing the elements in the sorted array at the correct index.
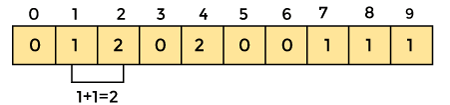
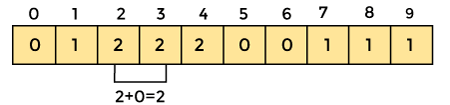
Similarly, the count array's cumulative count is -

4. Now you must determine the index of each element in the original array.
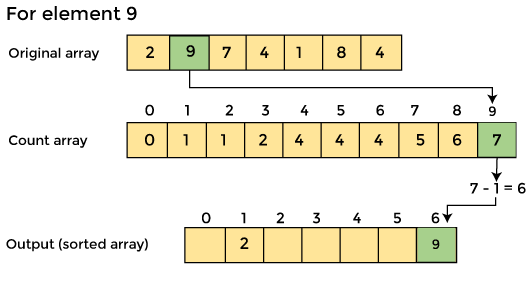
Reduce the element's count by one after it has been placed. Element 2 had a count of 2 before it was placed in the correct position, but now it has a new count of 1.
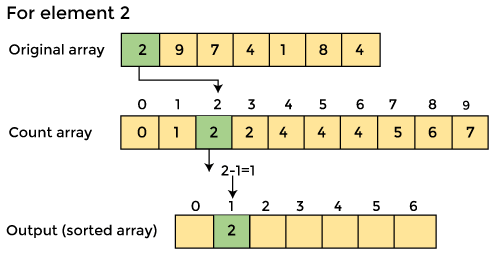
Key takeaway
Counting sort is a stable sorting technique that is used to sort things based on small numbers as keys.
It counts the number of keys with the same key value.
The counting sort is a sorting method based on the keys that connect certain ranges. Sorting algorithms are frequently asked in coding or technical interviews for software professionals.
The linear search algorithm scans all members of the array iteratively. It takes one second to execute and n seconds to execute, where n is the total number of items in the search array.
It is the simplest data structure search method, and it verifies each item in the set of elements until it matches the searched element until the data collection is complete. A linear search algorithm is favoured over other search algorithms when the data is unsorted.
The following are some of the more difficult aspects of linear search:
Space complexity
Because linear search takes up no more space, it has an O(n) space complexity, where n is the number of entries in an array.
Time complexity
● When the searched item is present at the first entry in the search array, the best-case complexity = O(1) occurs.
● When the necessary element is at the end of the array or not present at all, worst-case complexity = O(n) occurs.
● When the object to be searched is in the middle of the Array, the average-case complexity = average case happens.
Procedure for linear search
Procedure linear_search (list, value)
For each item in the list
If match item == value
Return the item's location
End if
End for
End procedure
Binary search
By comparing the data collection's middlemost pieces, this technique locates specific things. When a match is detected, the item's index is returned. It looks for a center item of the left sub-array when the middle item is greater than the search item. If the middle item, on the other hand, is smaller than the search item, it looks for it in the right sub-array. It continues to hunt for an item until it finds it or the sub-array size approaches zero.
The array's items must be sorted in order for binary search to work. It outperforms a linear search algorithm in terms of speed. The divide and conquer technique is used in the binary search.
Run-time complexity = O(log n)
Complexities in binary search are given below:
● The worst-case complexity in binary search is O(n log n).
● The average case complexity in binary search is O(n log n)
● Best case complexity = O (1)
Binary search algorithm
Procedure binary_search
A ← sorted array
n ← size of array
x ← value to be searched
Set lowerBound = 1
Set upperBound = n
While x not found
If upperBound < lowerBound
EXIT: x does not exists.
Set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
If A[midPoint] x
Set upperBound = midPoint - 1
If A[midPoint] = x
EXIT: x found at location midPoint
End while
End procedure
Key takeaway
The linear search algorithm scans all members of the array iteratively.
It takes one second to execute and n seconds to execute, where n is the total number of items in the search array.
By comparing the data collection's middlemost pieces, this technique locates specific things.
When a match is detected, the item's index is returned.
References:
- Data Structures Using C – A.M. Tenenbaum (PHI)
- Introduction to Data Structures with Applications by J. Tremblay and P. G. Sorenson (TMH)
- Data Structure and Program Design in C by C.L. Tondo.
- Data Structures and Algorithms in C, M.T. Goodrich, R. Tamassia and D. Mount, Wiley, India.
- Data Structure Using C by Pankaj Kumar Pandey.
- Data Structure with C, Tata McGraw Hill Education Private Limited by Seymour Lipschutz.
- Https://opendatastructures.org/ods-cpp/1_3_Mathematical_Background.html