Unit - 5
Hashing techniques
Hashing is implemented using one of two methods:
● Hashing with Chaining
● Hashing with open addressing
Hashing with chaining
The element in S is stored in Hash table T [0...m-1] of size m, where m is somewhat greater than n, the size of S, in Hashing with Chaining. There are m slots in the hash table. A hash function h is associated with the hashing technique, and it maps from U to {0...m-1}. We say that k is hashed into slot h since each key k ∈ S is kept in location T [h (k)] (k). A collision occurs when more than one key in S is hashed into the same slot.
All keys that hash into the same slot is placed in a linked list associated with that slot, which is referred to as the chain at slot. A hash table's load factor is defined as ∝=n/m, which represents the average amount of keys per slot. Because we frequently work in the m=θ(n) range, ∝ is usually a constant of ∝<1.
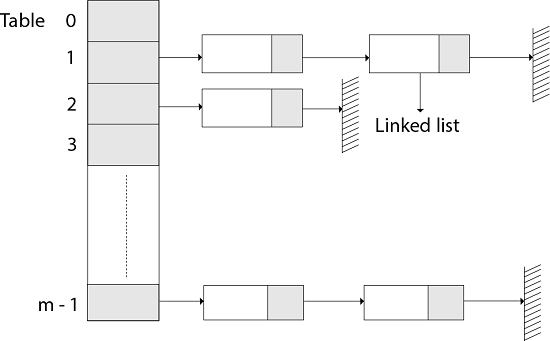
Fig 1: Hashing with chaining
Hashing with open address
All components in Open Addressing are kept in the hash table. That is, each table entry contains a dynamic set component or NIL. When looking for anything, we check table slots until we either find the item or establish that it isn't in the table. As a result, the load factor in open addressing can never exceed 1.
Open addressing has the advantage of avoiding Pointer. We compute the sequence of slots to be examined in this step. Because no pointers are shared, the hash table can have a larger number of slots for the same amount of memory, potentially resulting in fewer collisions and faster retrieval.
Probing is the process of inspecting a position in the hash table.
As a result, the hash function is transformed.
h : U x {0,1,....m-1} → {0,1,....,m-1}.
With open addressing, we need the probe sequence for every key k.
{h, (k, 0), h (k, 1)....h (k, m-1)}
Be a Permutation of (0, 1...... m-1)
A hash table T and a key k are passed to the HASH-INSERT method as inputs.
HASH-INSERT (T, k)
1. i ← 0
2. Repeat j ← h (k, i)
3. If T [j] = NIL
4. Then T [j] ← k
5. Return j
6. Else ← i= i +1
7. Until i=m
8. Error "hash table overflow"
The procedure HASH-SEARCH takes a hash table T and a key k as input and returns j if key k is found in slot j or NIL if key k is not found in table T.
HASH-SEARCH.T (k)
1. i ← 0
2. Repeat j ← h (k, i)
3. If T [j] =j
4. Then return j
5. i ← i+1
6. Until T [j] = NIL or i=m
7. Return NIL
The Hash Function is used to index the original value or key, and it is then utilized to obtain the data associated with the value or key. As a result, hashing is always a one-way process. By studying the hashed values, there is no need to "reverse engineer" the hash algorithm.
Characteristics of Good Hash Function:
● The data being hashed completely determines the hash value.
● All of the input data is used by the hash function.
● The hash function distributes the data "uniformly" across all potential hash values.
● For comparable strings, the hash function gives complicated hash values.
Some hash function
Division method
Select a number m that is less than the number of n keys in k. (The number m is usually chosen to be a prime number or a number without small divisors, since this frequently a minimum number of collisions).
The hash function is as follows:

Example - If m = 12 is the size of the hash table and k = 100 is the key, then h (k) = 4. Hashing via division is quick since it just requires one division operation.
Multiplication method
There are two phases to producing hash functions using the multiplication approach. First, we extract the fractional component of kA by multiplying the key k by a constant A in the range 0 A 1. Then we multiply this value by m and take the result's floor.
The hash function is as follows:

The fractional component of k A, k A -k A, is denoted by "k A mod 1."
Mid square method
The letter k has been squared. The function H is therefore defined as follows:
H (k) = L
L is found by subtracting digits from both ends of k2. We underline that k2 must be used in the same place for all keys.
Folding method
The key k is divided into a number of components k1, k2,... Kn, each with the same amount of digits as the needed address except maybe the last.
The pieces are then combined together, with the last carry ignored.
H (k) = k1+ k2+.....+kn
Key takeaway
The Hash Function is used to index the original value or key, and it is then utilized to obtain the data associated with the value or key.
As a result, hashing is always a one-way process.
● The hash function is utilized to find the array's index in this case.
● The hash value is used as an index in the hash table to hold the key.
● For two or more keys, the hash function can return the same hash value.
● A collision occurs when two or more keys are given the same hash value. Collision resolution strategies are used to deal with this collision.
Collision resolution techniques
Collision resolution strategies are divided into two categories.
● Separate chaining (open hashing)
● Open addressing (closed hashing)
Separate chaining
This strategy involves creating a linked list from the slot where the collision occurred, then inserting the new key into the linked list. Separate chaining refers to the linked list of slots that resembles a chain. When we don't know how many keys to insert or remove, we use it more.
Time complexity
● Its worst-case searching complexity is o (n).
● Its worst-case deletion complexity is o (n).
Advantages of separate chaining
● It is simple to put into practice.
● We can add more elements to the chain because the hash table never fills up.
● It is less sensitive to the hashing function.
Disadvantages of separate chaining
● Chaining cache performance is poor in this case.
● In this strategy, there is far too much memory waste.
● It necessitates a larger amount of space for element linkages.
Open addressing
Open addressing is a collision-resolution technique for preventing collisions in hashing tables. Outside of the hash table, no key is stored. As a result, the hash table's size is always more than or equal to the number of keys. Closed hashing is another name for it.
In open addressing, the following strategies are used:
● Linear probing
● Quadratic probing
● Double hashing
Key takeaway
The hash function is utilized to find the array's index in this case.
The hash value is used as an index in the hash table to hold the key.
For two or more keys, the hash function can return the same hash value.
It's a computer programming scheme for resolving hash table collisions.
Assume that a new record R with key k is to be added to the memory table T, but the memory locations with the hash address H are already filled (k). H has already been taken.
Crossing R to the first open position after T is our natural key to resolving the collision (h). T I appears after T [m] because we presume the table T with m location is circular.
Although linear probing is simple to use, it suffers from a problem called primary clustering. Long stretches of occupied slots accumulate over time, lengthening the average search time. Clusters form when an empty slot is followed by I full slots, with the probability I + 1)/m. Long stretches of occupied slots tend to lengthen, increasing the average search time.
The method of linear probing uses the hash function h': U 0...m-1 given an ordinary hash function h': U {0...m-1}.
h (k, i) = (h' (k) + i) mod m
For i=0, 1....m-1,'m' is the size of the hash table, and h' (k) = k mod m.
Given key k, the first slot is T [h' (k)]. We next slot T [h' (k) +1] and so on up to the slot T [m-1]. Then we wrap around to slots T [0], T [1]....until finally slot T [h' (k)-1]. Since the initial probe position dispose of the entire probe sequence, only m distinct probe sequences are used with linear probing.
Advantages
● It is simple to calculate.
Disadvantages
● Clustering is the fundamental issue with linear probing.
● Many items in a row create a group.
● Then there's the time it takes to look for an element or an empty bucket.
Example
Consider using linear probing to insert the keys 24, 36, 58,65,62,86 into a hash table of size m=11, with the primary hash function h' (k) = k mod m.
Solution: Hash table's initial state
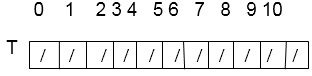
Insert 24. We know h (k, i) = [h' (k) + i] mod m
Now h (24, 0) = [24 mod 11 + 0] mod 11
= (2+0) mod 11 = 2 mod 11 = 2
Since T [2] is free, insert key 24 at this place.
Insert 36. Now h (36, 0) = [36 mod 11 + 0] mod 11
= [3+0] mod 11 = 3
Since T [3] is free, insert key 36 at this place.
Insert 58. Now h (58, 0) = [58 mod 11 +0] mod 11
= [3+0] mod 11 =3
Since T [3] is not free, so the next sequence is
h (58, 1) = [58 mod 11 +1] mod 11
= [3+1] mod 11= 4 mod 11=4
T [4] is free; Insert key 58 at this place.
Insert 65. Now h (65, 0) = [65 mod 11 +0] mod 11
= (10 +0) mod 11= 10
T [10] is free. Insert key 65 at this place.
Insert 62. Now h (62, 0) = [62 mod 11 +0] mod 11
= [7 + 0] mod 11 = 7
T [7] is free. Insert key 62 at this place.
Insert 86. Now h (86, 0) = [86 mod 11 + 0] mod 11
= [9 + 0] mod 11 = 9
T [9] is free. Insert key 86 at this place.
Thus,

Key takeaway
It's a computer programming scheme for resolving hash table collisions.
Although linear probing is simple to use, it suffers from a problem called primary clustering.
It is a technique that makes sure that if we have a collision at a particular bucket, then we check for the next available bucket location, and insert our data in that bucket.
If a record R contains the hash address H (k) = h, instead of scanning the location using the addresses h, h+1, and h+ 2... We search for addresses in a linear manner.
h, h+1, h+4, h+9...h+i2
A hash function of the form is used in quadratic probing.
h (k,i) = (h' (k) + c1i + c2i2) mod m
Where h' is an auxiliary hash function, c1 and c2 0 are auxiliary constants, and i=0, 1...m-1 are integers. The initial location is T [h' (k)], and the later probed position is offset by an amount that is quadratic in relation to the probe number i.
Example
Consider using quadratic probing with c1=1 and c2=3 to insert the keys 74, 28, 36,58,21,64 into a hash table of size m =11. Consider that h' (k) = k mod m is the basic hash function.
Solution: We have a solution for Quadratic Probing.
h (k, i) = [k mod m +c1i +c2 i2) mod m
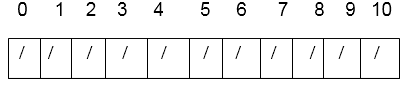
This is the hash table's initial state.
Here c1= 1 and c2=3
h (k, i) = [k mod m + i + 3i2 ] mod m
Insert 74.
h (74,0)= (74 mod 11+0+3x0) mod 11
= (8 +0+0) mod 11 = 8
T [8] is free; insert the key 74 at this place.
Insert 28.
h (28, 0) = (28 mod 11 + 0 + 3 x 0) mod 11
= (6 +0 + 0) mod 11 = 6.
T [6] is free; insert key 28 at this place.
Insert 36.
h (36, 0) = (36 mod 11 + 0 + 3 x 0) mod 11
= (3 + 0+0) mod 11=3
T [3] is free; insert key 36 at this place.
Insert 58.
h (58, 0) = (58 mod 11 + 0 + 3 x 0) mod 11
= (3 + 0 + 0) mod 11 = 3
T [3] is not free, so next probe sequence is computed as
h (59, 1) = (58 mod 11 + 1 + 3 x12) mod 11
= (3 + 1 + 3) mod 11
=7 mod 11= 7
T [7] is free; insert key 58 at this place.
Insert 21.
h (21, 0) = (21 mod 11 + 0 + 3 x 0)
= (10 + 0) mod 11 = 10
T [10] is free; insert key 21 at this place.
Insert 64.
h (64, 0) = (64 mod 11 + 0 + 3 x 0)
= (9 + 0+ 0) mod 11 = 9.
T [9] is free; insert key 64 at this place.
As a result, after entering all keys, the hash table is complete.

Because the permutations created have many of the features of randomly chosen permutations, Double Hashing is one of the best open addressing strategies available.
A hash function of the form is used in double hashing.
h (k, i) = (h1(k) + i h2 (k)) mod m
Where auxiliary hash functions h1 and h2 are used, and m is the size of the hash table.
h1 (k) = k mod m' and h2 (k) = k mod m' m' is slightly less than m in this case (say m-1 or m-2).
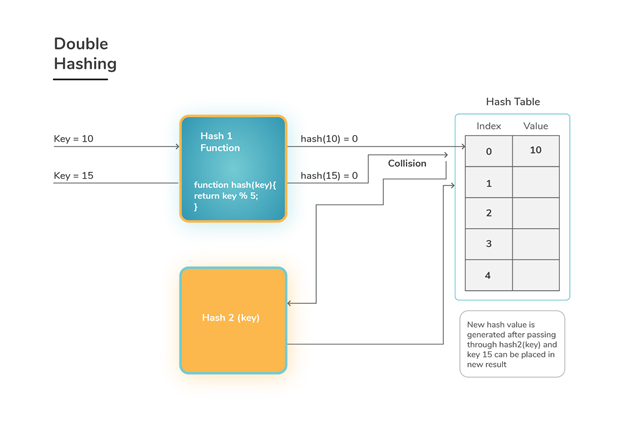
Fig 2: Double hashing
Example
Consider utilizing double hashing to put the keys 76, 26, 37, 59, 21, 65 into a hash table of size m = 11. Consider that h1 (k)=k mod 11 and h2(k) = k mod 9 are the auxiliary hash functions.
Solution: Hash table's initial state is

1. Insert 76.
h1(76) = 76 mod 11 = 10
h2(76) = 76 mod 9 = 4
h (76, 0) = (10 + 0 x 4) mod 11
= 10 mod 11 = 10
T [10] is free, so insert key 76 at this place.
2. Insert 26.
h1(26) = 26 mod 11 = 4
h2(26) = 26 mod 9 = 8
h (26, 0) = (4 + 0 x 8) mod 11
= 4 mod 11 = 4
T [4] is free, so insert key 26 at this place.
3. Insert 37.
h1(37) = 37 mod 11 = 4
h2(37) = 37 mod 9 = 1
h (37, 0) = (4 + 0 x 1) mod 11 = 4 mod 11 = 4
T [4] is not free, the next probe sequence is
h (37, 1) = (4 + 1 x 1) mod 11 = 5 mod 11 = 5
T [5] is free, so insert key 37 at this place.
4. Insert 59.
h1(59) = 59 mod 11 = 4
h2(59) = 59 mod 9 = 5
h (59, 0) = (4 + 0 x 5) mod 11 = 4 mod 11 = 4
Since, T [4] is not free, the next probe sequence is
h (59, 1) = (4 + 1 x 5) mod 11 = 9 mod 11 = 9
T [9] is free, so insert key 59 at this place.
5. Insert 21.
h1(21) = 21 mod 11 = 10
h2(21) = 21 mod 9 = 3
h (21, 0) = (10 + 0 x 3) mod 11 = 10 mod 11 = 10
T [10] is not free, the next probe sequence is
h (21, 1) = (10 + 1 x 3) mod 11 = 13 mod 11 = 2
T [2] is free, so insert key 21 at this place.
6. Insert 65.
h1(65) = 65 mod 11 = 10
h2(65) = 65 mod 9 = 2
h (65, 0) = (10 + 0 x 2) mod 11 = 10 mod 11 = 10
T [10] is not free, the next probe sequence is
h (65, 1) = (10 + 1 x 2) mod 11 = 12 mod 11 = 1
T [1] is free, so insert key 65 at this place.
Thus, after insertion of all keys the final hash table is
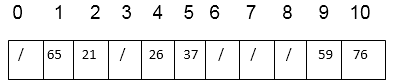
Key takeaway
Because the permutations created have many of the features of randomly chosen permutations, Double Hashing is one of the best open addressing strategies available.
All records are stored directly in the hash table when closed hashing is used. The home location of each record R with the key value kR is h(kR), the slot generated by the hash function. If R is to be inserted while another record already occupies R's home location in the table, R will be stored in a different slot. The collision resolution policy is in charge of determining which slot will be used. Naturally, the same policy must be followed during search as it is during insertion, so that any record that is not discovered in its original location can be recovered by repeating the collision resolution process.
Closed hashing in one implementation divides hash table slots into buckets. The hash table's M slots are partitioned into B buckets, each of which has M/B slots. Each record is assigned to the first slot in one of the buckets by the hash function. If this position is already taken, the bucket slots are examined in order until one becomes available. If a bucket is completely filled, the record is saved in an indefinite capacity overflow bucket at the end of the table. The overflow bucket is shared by all buckets. A decent implementation will employ a hash function to uniformly divide the records throughout the buckets, ensuring that the overflow bucket contains as few records as feasible.
When looking for a record, the first step is to hash the key to figure out which bucket it belongs in. After that, the records in this bucket are searched. The search is complete if the requested key value is not discovered and the bucket still has open slots. It's possible that the required record is placed in the overflow bucket if the bucket is full. In this situation, the overflow bucket must be searched until the record is located or until all of the overflow bucket's records have been verified. If there are a lot of records in the overflow bucket, this will be a time-consuming procedure.
A hash table [hash map] is a data structure in computing that allows for practically immediate access to items using a key [a unique String or Integer]. A hash table employs a hash function to generate an index into an array of buckets or slots from which the necessary value can be retrieved. The key's main characteristics are as follows:
● Your SSN, phone number, account number, and other personal information can be utilized as the key.
● Unique keys are required.
● Each key has a value associated with it, which is mapped to it.
Hash buckets are used to group data objects together for sorting and lookup. The goal of this project is to make linked lists weaker so that searching for a specific item may be done in less time. A bucket-based hash table is essentially a hybrid of an array and a linked list. Each element of the array [the hash table] is a linked list's header. The list will contain all components that hash to the same location. Each record is assigned to the first slot in one of the buckets by the hash function. If the slot is already used, the bucket slots will be checked consecutively until one becomes available.
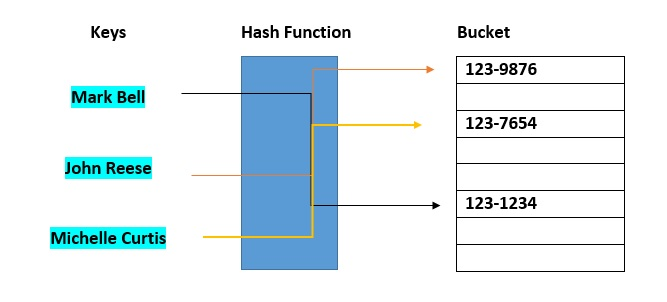
Fig 3: Hash bucket
If a bucket is totally filled, the record will be saved in an infinite capacity overflow bucket at the table's end. The overflow bucket is shared by all buckets. A smart implementation, on the other hand, will utilize a hash function to uniformly distribute the records throughout the buckets, ensuring that as few records as possible end up in the overflow bucket.
Rehashing, as the name implies, entails hashing once more. The complexity of a system grows as the load factor exceeds its predefined value (the default load factor is 0.75). To overcome this, the array's size is doubled, and all of the values are hashed and saved in the new double-sized array to keep the load factor and complexity low.
In the event that the hash table becomes almost full at any point, the running time for operations will become too long, and the insert operation may fail as a result. The best feasible approach is as follows:
● Make a new hash table that is twice as big as the old one.
● Scanning the old hash table, calculating a new hash value, and inserting it into the new hash table.
● The memory used by the original hash table should be freed.
Why rehashing?
The reason for rehashing is that as key value pairs are entered into the map, the load factor rises, implying that the time complexity rises as well, as mentioned above. This may not provide the time complexity that O requires (1).
As a result, rehash is required, with the bucket Array's size increased to lower the load factor and temporal complexity.
Example
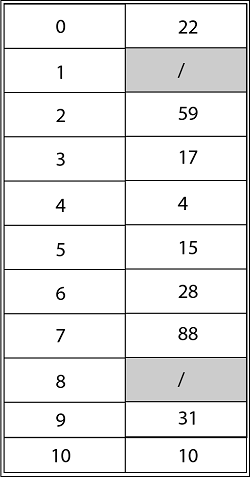
Consider utilizing open addressing with the primary hash function h' (k) = k mod m to insert the keys 10, 22, 31,4,15,28,17,88, and 59 into a hash table of length m = 11 using the keys 10, 22, 31,4,15,28,17,88, and 59. Show the results of using linear probing, quadratic probing with c1=1 and c2=3, and double hashing with h2(k) = 1 + (k mod (m-1) to insert these keys.
Solution: The final state of the hash table using Linear Probing would be:
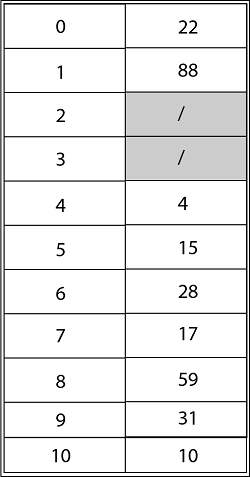
Using Quadratic Probing with c1=1, c2=3, the final state of hash table would be h (k, I = (h' (k) +c1*i+ c2 *i2) mod m where m=11 and h' (k) = k mod m.
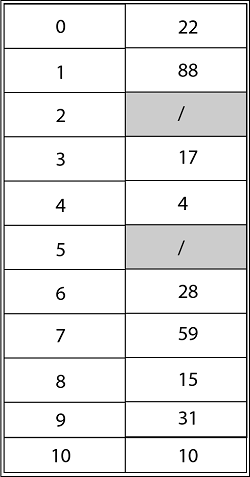
Using Double Hashing, the ultimate state of the hash table would be:
How Rehashing is done?
Rehashing can be done in the following way:
● Check the load factor after adding a new entry to the map.
● Rehash if it's bigger than the predefined value (or the default value of 0.75 if none is specified).
● Make a new bucket array that is double the size of the previous one for Rehash.
● Then go through each element in the old bucket Array, calling insert() on each to add it to the new larger bucket array.
Key takeaway
Rehashing, as the name implies, entails hashing once more. The complexity of a system grows as the load factor exceeds its predefined value.
In the event that the hash table becomes almost full at any point, the running time for operations will become too long, and the insert operation may fail as a result.
References:
- Data Structures, Algorithms and Application in C, 2nd Edition, Sartaj Sahni
- Data Structures and Algorithms in C, M.T. Goodrich, R. Tamassia and D. Mount, Wiley India.
- Data Structures and Algorithm Analysis in C, 3rd Edition, M.A. Weiss, Pearson.
- Classic Data Structures, D. Samanta, 2nd Edition, PHI.
- Data Structure Using C by Pankaj Kumar Pandey.
- Data Structure with C, Tata McGraw Hill Education Private Limited by Seymour Lipschutz.
- Https://www.tutorialandexample.com/collision-resolution-techniques-in-data-structure/
- Https://www.javatpoint.com/daa-open-addressing-techniques
Unit - 5
Hashing techniques
Hashing is implemented using one of two methods:
● Hashing with Chaining
● Hashing with open addressing
Hashing with chaining
The element in S is stored in Hash table T [0...m-1] of size m, where m is somewhat greater than n, the size of S, in Hashing with Chaining. There are m slots in the hash table. A hash function h is associated with the hashing technique, and it maps from U to {0...m-1}. We say that k is hashed into slot h since each key k ∈ S is kept in location T [h (k)] (k). A collision occurs when more than one key in S is hashed into the same slot.
All keys that hash into the same slot is placed in a linked list associated with that slot, which is referred to as the chain at slot. A hash table's load factor is defined as ∝=n/m, which represents the average amount of keys per slot. Because we frequently work in the m=θ(n) range, ∝ is usually a constant of ∝<1.
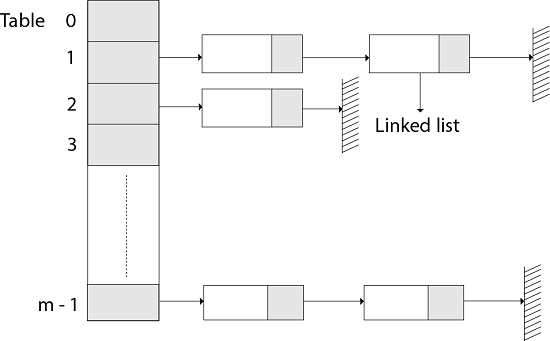
Fig 1: Hashing with chaining
Hashing with open address
All components in Open Addressing are kept in the hash table. That is, each table entry contains a dynamic set component or NIL. When looking for anything, we check table slots until we either find the item or establish that it isn't in the table. As a result, the load factor in open addressing can never exceed 1.
Open addressing has the advantage of avoiding Pointer. We compute the sequence of slots to be examined in this step. Because no pointers are shared, the hash table can have a larger number of slots for the same amount of memory, potentially resulting in fewer collisions and faster retrieval.
Probing is the process of inspecting a position in the hash table.
As a result, the hash function is transformed.
h : U x {0,1,....m-1} → {0,1,....,m-1}.
With open addressing, we need the probe sequence for every key k.
{h, (k, 0), h (k, 1)....h (k, m-1)}
Be a Permutation of (0, 1...... m-1)
A hash table T and a key k are passed to the HASH-INSERT method as inputs.
HASH-INSERT (T, k)
1. i ← 0
2. Repeat j ← h (k, i)
3. If T [j] = NIL
4. Then T [j] ← k
5. Return j
6. Else ← i= i +1
7. Until i=m
8. Error "hash table overflow"
The procedure HASH-SEARCH takes a hash table T and a key k as input and returns j if key k is found in slot j or NIL if key k is not found in table T.
HASH-SEARCH.T (k)
1. i ← 0
2. Repeat j ← h (k, i)
3. If T [j] =j
4. Then return j
5. i ← i+1
6. Until T [j] = NIL or i=m
7. Return NIL
The Hash Function is used to index the original value or key, and it is then utilized to obtain the data associated with the value or key. As a result, hashing is always a one-way process. By studying the hashed values, there is no need to "reverse engineer" the hash algorithm.
Characteristics of Good Hash Function:
● The data being hashed completely determines the hash value.
● All of the input data is used by the hash function.
● The hash function distributes the data "uniformly" across all potential hash values.
● For comparable strings, the hash function gives complicated hash values.
Some hash function
Division method
Select a number m that is less than the number of n keys in k. (The number m is usually chosen to be a prime number or a number without small divisors, since this frequently a minimum number of collisions).
The hash function is as follows:

Example - If m = 12 is the size of the hash table and k = 100 is the key, then h (k) = 4. Hashing via division is quick since it just requires one division operation.
Multiplication method
There are two phases to producing hash functions using the multiplication approach. First, we extract the fractional component of kA by multiplying the key k by a constant A in the range 0 A 1. Then we multiply this value by m and take the result's floor.
The hash function is as follows:

The fractional component of k A, k A -k A, is denoted by "k A mod 1."
Mid square method
The letter k has been squared. The function H is therefore defined as follows:
H (k) = L
L is found by subtracting digits from both ends of k2. We underline that k2 must be used in the same place for all keys.
Folding method
The key k is divided into a number of components k1, k2,... Kn, each with the same amount of digits as the needed address except maybe the last.
The pieces are then combined together, with the last carry ignored.
H (k) = k1+ k2+.....+kn
Key takeaway
The Hash Function is used to index the original value or key, and it is then utilized to obtain the data associated with the value or key.
As a result, hashing is always a one-way process.
● The hash function is utilized to find the array's index in this case.
● The hash value is used as an index in the hash table to hold the key.
● For two or more keys, the hash function can return the same hash value.
● A collision occurs when two or more keys are given the same hash value. Collision resolution strategies are used to deal with this collision.
Collision resolution techniques
Collision resolution strategies are divided into two categories.
● Separate chaining (open hashing)
● Open addressing (closed hashing)
Separate chaining
This strategy involves creating a linked list from the slot where the collision occurred, then inserting the new key into the linked list. Separate chaining refers to the linked list of slots that resembles a chain. When we don't know how many keys to insert or remove, we use it more.
Time complexity
● Its worst-case searching complexity is o (n).
● Its worst-case deletion complexity is o (n).
Advantages of separate chaining
● It is simple to put into practice.
● We can add more elements to the chain because the hash table never fills up.
● It is less sensitive to the hashing function.
Disadvantages of separate chaining
● Chaining cache performance is poor in this case.
● In this strategy, there is far too much memory waste.
● It necessitates a larger amount of space for element linkages.
Open addressing
Open addressing is a collision-resolution technique for preventing collisions in hashing tables. Outside of the hash table, no key is stored. As a result, the hash table's size is always more than or equal to the number of keys. Closed hashing is another name for it.
In open addressing, the following strategies are used:
● Linear probing
● Quadratic probing
● Double hashing
Key takeaway
The hash function is utilized to find the array's index in this case.
The hash value is used as an index in the hash table to hold the key.
For two or more keys, the hash function can return the same hash value.
It's a computer programming scheme for resolving hash table collisions.
Assume that a new record R with key k is to be added to the memory table T, but the memory locations with the hash address H are already filled (k). H has already been taken.
Crossing R to the first open position after T is our natural key to resolving the collision (h). T I appears after T [m] because we presume the table T with m location is circular.
Although linear probing is simple to use, it suffers from a problem called primary clustering. Long stretches of occupied slots accumulate over time, lengthening the average search time. Clusters form when an empty slot is followed by I full slots, with the probability I + 1)/m. Long stretches of occupied slots tend to lengthen, increasing the average search time.
The method of linear probing uses the hash function h': U 0...m-1 given an ordinary hash function h': U {0...m-1}.
h (k, i) = (h' (k) + i) mod m
For i=0, 1....m-1,'m' is the size of the hash table, and h' (k) = k mod m.
Given key k, the first slot is T [h' (k)]. We next slot T [h' (k) +1] and so on up to the slot T [m-1]. Then we wrap around to slots T [0], T [1]....until finally slot T [h' (k)-1]. Since the initial probe position dispose of the entire probe sequence, only m distinct probe sequences are used with linear probing.
Advantages
● It is simple to calculate.
Disadvantages
● Clustering is the fundamental issue with linear probing.
● Many items in a row create a group.
● Then there's the time it takes to look for an element or an empty bucket.
Example
Consider using linear probing to insert the keys 24, 36, 58,65,62,86 into a hash table of size m=11, with the primary hash function h' (k) = k mod m.
Solution: Hash table's initial state
Insert 24. We know h (k, i) = [h' (k) + i] mod m
Now h (24, 0) = [24 mod 11 + 0] mod 11
= (2+0) mod 11 = 2 mod 11 = 2
Since T [2] is free, insert key 24 at this place.
Insert 36. Now h (36, 0) = [36 mod 11 + 0] mod 11
= [3+0] mod 11 = 3
Since T [3] is free, insert key 36 at this place.
Insert 58. Now h (58, 0) = [58 mod 11 +0] mod 11
= [3+0] mod 11 =3
Since T [3] is not free, so the next sequence is
h (58, 1) = [58 mod 11 +1] mod 11
= [3+1] mod 11= 4 mod 11=4
T [4] is free; Insert key 58 at this place.
Insert 65. Now h (65, 0) = [65 mod 11 +0] mod 11
= (10 +0) mod 11= 10
T [10] is free. Insert key 65 at this place.
Insert 62. Now h (62, 0) = [62 mod 11 +0] mod 11
= [7 + 0] mod 11 = 7
T [7] is free. Insert key 62 at this place.
Insert 86. Now h (86, 0) = [86 mod 11 + 0] mod 11
= [9 + 0] mod 11 = 9
T [9] is free. Insert key 86 at this place.
Thus,

Key takeaway
It's a computer programming scheme for resolving hash table collisions.
Although linear probing is simple to use, it suffers from a problem called primary clustering.
It is a technique that makes sure that if we have a collision at a particular bucket, then we check for the next available bucket location, and insert our data in that bucket.
If a record R contains the hash address H (k) = h, instead of scanning the location using the addresses h, h+1, and h+ 2... We search for addresses in a linear manner.
h, h+1, h+4, h+9...h+i2
A hash function of the form is used in quadratic probing.
h (k,i) = (h' (k) + c1i + c2i2) mod m
Where h' is an auxiliary hash function, c1 and c2 0 are auxiliary constants, and i=0, 1...m-1 are integers. The initial location is T [h' (k)], and the later probed position is offset by an amount that is quadratic in relation to the probe number i.
Example
Consider using quadratic probing with c1=1 and c2=3 to insert the keys 74, 28, 36,58,21,64 into a hash table of size m =11. Consider that h' (k) = k mod m is the basic hash function.
Solution: We have a solution for Quadratic Probing.
h (k, i) = [k mod m +c1i +c2 i2) mod m
This is the hash table's initial state.
Here c1= 1 and c2=3
h (k, i) = [k mod m + i + 3i2 ] mod m
Insert 74.
h (74,0)= (74 mod 11+0+3x0) mod 11
= (8 +0+0) mod 11 = 8
T [8] is free; insert the key 74 at this place.
Insert 28.
h (28, 0) = (28 mod 11 + 0 + 3 x 0) mod 11
= (6 +0 + 0) mod 11 = 6.
T [6] is free; insert key 28 at this place.
Insert 36.
h (36, 0) = (36 mod 11 + 0 + 3 x 0) mod 11
= (3 + 0+0) mod 11=3
T [3] is free; insert key 36 at this place.
Insert 58.
h (58, 0) = (58 mod 11 + 0 + 3 x 0) mod 11
= (3 + 0 + 0) mod 11 = 3
T [3] is not free, so next probe sequence is computed as
h (59, 1) = (58 mod 11 + 1 + 3 x12) mod 11
= (3 + 1 + 3) mod 11
=7 mod 11= 7
T [7] is free; insert key 58 at this place.
Insert 21.
h (21, 0) = (21 mod 11 + 0 + 3 x 0)
= (10 + 0) mod 11 = 10
T [10] is free; insert key 21 at this place.
Insert 64.
h (64, 0) = (64 mod 11 + 0 + 3 x 0)
= (9 + 0+ 0) mod 11 = 9.
T [9] is free; insert key 64 at this place.
As a result, after entering all keys, the hash table is complete.

Because the permutations created have many of the features of randomly chosen permutations, Double Hashing is one of the best open addressing strategies available.
A hash function of the form is used in double hashing.
h (k, i) = (h1(k) + i h2 (k)) mod m
Where auxiliary hash functions h1 and h2 are used, and m is the size of the hash table.
h1 (k) = k mod m' and h2 (k) = k mod m' m' is slightly less than m in this case (say m-1 or m-2).
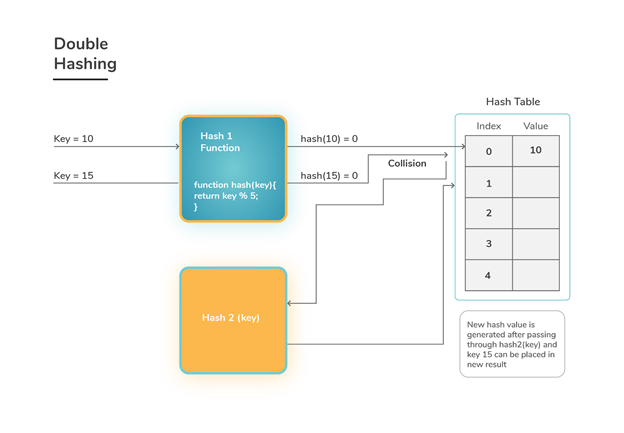
Fig 2: Double hashing
Example
Consider utilizing double hashing to put the keys 76, 26, 37, 59, 21, 65 into a hash table of size m = 11. Consider that h1 (k)=k mod 11 and h2(k) = k mod 9 are the auxiliary hash functions.
Solution: Hash table's initial state is

1. Insert 76.
h1(76) = 76 mod 11 = 10
h2(76) = 76 mod 9 = 4
h (76, 0) = (10 + 0 x 4) mod 11
= 10 mod 11 = 10
T [10] is free, so insert key 76 at this place.
2. Insert 26.
h1(26) = 26 mod 11 = 4
h2(26) = 26 mod 9 = 8
h (26, 0) = (4 + 0 x 8) mod 11
= 4 mod 11 = 4
T [4] is free, so insert key 26 at this place.
3. Insert 37.
h1(37) = 37 mod 11 = 4
h2(37) = 37 mod 9 = 1
h (37, 0) = (4 + 0 x 1) mod 11 = 4 mod 11 = 4
T [4] is not free, the next probe sequence is
h (37, 1) = (4 + 1 x 1) mod 11 = 5 mod 11 = 5
T [5] is free, so insert key 37 at this place.
4. Insert 59.
h1(59) = 59 mod 11 = 4
h2(59) = 59 mod 9 = 5
h (59, 0) = (4 + 0 x 5) mod 11 = 4 mod 11 = 4
Since, T [4] is not free, the next probe sequence is
h (59, 1) = (4 + 1 x 5) mod 11 = 9 mod 11 = 9
T [9] is free, so insert key 59 at this place.
5. Insert 21.
h1(21) = 21 mod 11 = 10
h2(21) = 21 mod 9 = 3
h (21, 0) = (10 + 0 x 3) mod 11 = 10 mod 11 = 10
T [10] is not free, the next probe sequence is
h (21, 1) = (10 + 1 x 3) mod 11 = 13 mod 11 = 2
T [2] is free, so insert key 21 at this place.
6. Insert 65.
h1(65) = 65 mod 11 = 10
h2(65) = 65 mod 9 = 2
h (65, 0) = (10 + 0 x 2) mod 11 = 10 mod 11 = 10
T [10] is not free, the next probe sequence is
h (65, 1) = (10 + 1 x 2) mod 11 = 12 mod 11 = 1
T [1] is free, so insert key 65 at this place.
Thus, after insertion of all keys the final hash table is
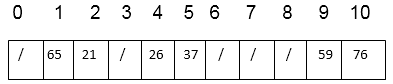
Key takeaway
Because the permutations created have many of the features of randomly chosen permutations, Double Hashing is one of the best open addressing strategies available.
All records are stored directly in the hash table when closed hashing is used. The home location of each record R with the key value kR is h(kR), the slot generated by the hash function. If R is to be inserted while another record already occupies R's home location in the table, R will be stored in a different slot. The collision resolution policy is in charge of determining which slot will be used. Naturally, the same policy must be followed during search as it is during insertion, so that any record that is not discovered in its original location can be recovered by repeating the collision resolution process.
Closed hashing in one implementation divides hash table slots into buckets. The hash table's M slots are partitioned into B buckets, each of which has M/B slots. Each record is assigned to the first slot in one of the buckets by the hash function. If this position is already taken, the bucket slots are examined in order until one becomes available. If a bucket is completely filled, the record is saved in an indefinite capacity overflow bucket at the end of the table. The overflow bucket is shared by all buckets. A decent implementation will employ a hash function to uniformly divide the records throughout the buckets, ensuring that the overflow bucket contains as few records as feasible.
When looking for a record, the first step is to hash the key to figure out which bucket it belongs in. After that, the records in this bucket are searched. The search is complete if the requested key value is not discovered and the bucket still has open slots. It's possible that the required record is placed in the overflow bucket if the bucket is full. In this situation, the overflow bucket must be searched until the record is located or until all of the overflow bucket's records have been verified. If there are a lot of records in the overflow bucket, this will be a time-consuming procedure.
A hash table [hash map] is a data structure in computing that allows for practically immediate access to items using a key [a unique String or Integer]. A hash table employs a hash function to generate an index into an array of buckets or slots from which the necessary value can be retrieved. The key's main characteristics are as follows:
● Your SSN, phone number, account number, and other personal information can be utilized as the key.
● Unique keys are required.
● Each key has a value associated with it, which is mapped to it.
Hash buckets are used to group data objects together for sorting and lookup. The goal of this project is to make linked lists weaker so that searching for a specific item may be done in less time. A bucket-based hash table is essentially a hybrid of an array and a linked list. Each element of the array [the hash table] is a linked list's header. The list will contain all components that hash to the same location. Each record is assigned to the first slot in one of the buckets by the hash function. If the slot is already used, the bucket slots will be checked consecutively until one becomes available.
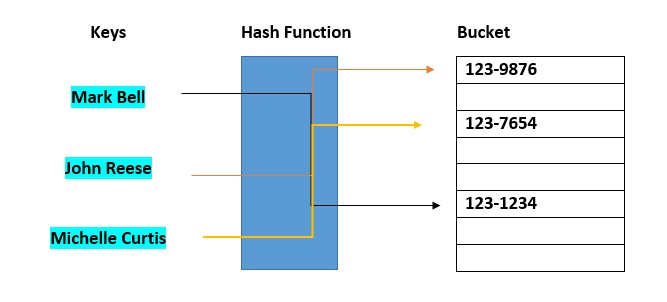
Fig 3: Hash bucket
If a bucket is totally filled, the record will be saved in an infinite capacity overflow bucket at the table's end. The overflow bucket is shared by all buckets. A smart implementation, on the other hand, will utilize a hash function to uniformly distribute the records throughout the buckets, ensuring that as few records as possible end up in the overflow bucket.
Rehashing, as the name implies, entails hashing once more. The complexity of a system grows as the load factor exceeds its predefined value (the default load factor is 0.75). To overcome this, the array's size is doubled, and all of the values are hashed and saved in the new double-sized array to keep the load factor and complexity low.
In the event that the hash table becomes almost full at any point, the running time for operations will become too long, and the insert operation may fail as a result. The best feasible approach is as follows:
● Make a new hash table that is twice as big as the old one.
● Scanning the old hash table, calculating a new hash value, and inserting it into the new hash table.
● The memory used by the original hash table should be freed.
Why rehashing?
The reason for rehashing is that as key value pairs are entered into the map, the load factor rises, implying that the time complexity rises as well, as mentioned above. This may not provide the time complexity that O requires (1).
As a result, rehash is required, with the bucket Array's size increased to lower the load factor and temporal complexity.
Example
Consider utilizing open addressing with the primary hash function h' (k) = k mod m to insert the keys 10, 22, 31,4,15,28,17,88, and 59 into a hash table of length m = 11 using the keys 10, 22, 31,4,15,28,17,88, and 59. Show the results of using linear probing, quadratic probing with c1=1 and c2=3, and double hashing with h2(k) = 1 + (k mod (m-1) to insert these keys.
Solution: The final state of the hash table using Linear Probing would be:
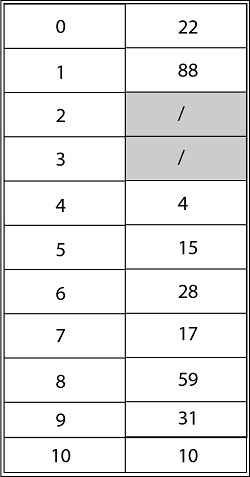
Using Quadratic Probing with c1=1, c2=3, the final state of hash table would be h (k, I = (h' (k) +c1*i+ c2 *i2) mod m where m=11 and h' (k) = k mod m.
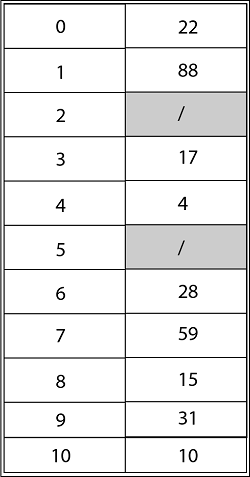
Using Double Hashing, the ultimate state of the hash table would be:
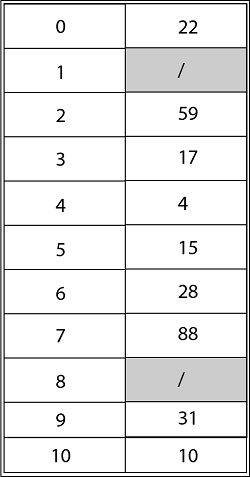
How Rehashing is done?
Rehashing can be done in the following way:
● Check the load factor after adding a new entry to the map.
● Rehash if it's bigger than the predefined value (or the default value of 0.75 if none is specified).
● Make a new bucket array that is double the size of the previous one for Rehash.
● Then go through each element in the old bucket Array, calling insert() on each to add it to the new larger bucket array.
Key takeaway
Rehashing, as the name implies, entails hashing once more. The complexity of a system grows as the load factor exceeds its predefined value.
In the event that the hash table becomes almost full at any point, the running time for operations will become too long, and the insert operation may fail as a result.
References:
- Data Structures, Algorithms and Application in C, 2nd Edition, Sartaj Sahni
- Data Structures and Algorithms in C, M.T. Goodrich, R. Tamassia and D. Mount, Wiley India.
- Data Structures and Algorithm Analysis in C, 3rd Edition, M.A. Weiss, Pearson.
- Classic Data Structures, D. Samanta, 2nd Edition, PHI.
- Data Structure Using C by Pankaj Kumar Pandey.
- Data Structure with C, Tata McGraw Hill Education Private Limited by Seymour Lipschutz.
- Https://www.tutorialandexample.com/collision-resolution-techniques-in-data-structure/
- Https://www.javatpoint.com/daa-open-addressing-techniques