Unit - 1
Introduction and Classification of signals
Definition: A signal is defined as a physical quantity that varies with time, space, or any other independent variable.
The signal may depend on one or more independent variables. If the signal depends on one variable, then it is known as a one-dimensional signal. If it depends on two independent variables, then the signal is known as a two-dimensional signal. Examples are pictures, X-ray images, and sonograms.
The multidimensional signal depends on many variables.
Graphical, Functional, Tabular and Sequence Representation of Discrete-time Signal
Graphical Representation
Let us consider a signal x(n) with values x(0) =2; x(1)=1.5;x(1)=2;x(3)=1.5
The discrete-time signal can be represented graphically as:
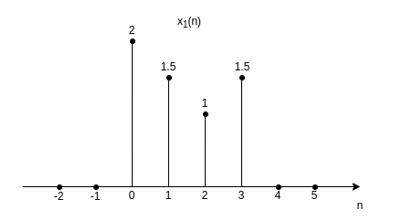
Figure 1. Discrete-time in graphical
Functional Representation
The discrete time signal as shown in figure can be represented using functional representation as below:
x(n) = 2 for n=0
1 for n=2
1.5 for n=3
Tabular Representation
The discrete-time signal can also be represented as:
N | 0 | 1 | 2 | 3 |
x(n) | 2 | 1.5 | 1 | 1.5 |
Sequence Representation
A finite duration sequence with time origin (n=0) indicated by the symbol 
is represented as
x(n) = {1, 2, 2, 0.5, 1.5}
A finite duration sequence can be represented as
x(n) = {……. 0.2, 1, -1, 3, 2……….}
A finite duration sequence that satisfies the condition x(n) =0 for n<0 can be represented as
x(n)={2, 4, 6, 8, -3}
Graphical, Functional, Tabular and Sequence Representation of continuous-time Signal
Graphical Representation
Many phenomena in our physical world are described in terms of continuous-time signals. Some examples of continuous-time signals include voltage or current waveforms in an electronic circuit;
Figure 2. Discrete-time in graphical
A continuous time system is one which operates on the continuous time input signal and produces a continuous-time output signal.
Figure 3. I/O of continuous time signal
If the input is x(t) and output is y(t) then
y(t) = T{x(t)}
That is x (t) is transformed to y(t).
Example: Amplifiers, filters, motors etc
Discrete time system is one which operates on discrete time input signal and produces a discrete-time output signal.
Figure 4. I/O of Discrete time signal
If the input is x(n) and output y(n) then
y(n) = T[x(n)]
Continuous and Discrete amplitude signals
Continuous-time discrete amplitude signals are basically digital signals.
Discrete amplitude is one which we get through quantization process and it depends how many levels of quantization one wants. In simple words, quantization means assigning the amplitude values of any analog signal to certain discrete levels, equidistant of each other based on certain criteria.
A square wave is a continuous-time discrete amplitude signal. For binary signals, there are only two quantization levels (0,1).
Some examples of continuous-time discrete amplitude signals:
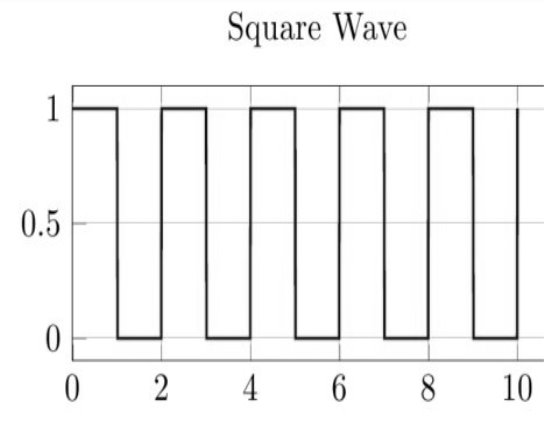
Figure 5. Continuous and Discrete Amplitude Signals
Key Takeaways:
Quantization means assigning the amplitude values of any analog signal to certain discrete levels
- Elementary continuous-time signals
Unit step function
The unit step sequence is defined as:
u(t) = 1 for t 
= 0 for t<0
From the above equation, we find the when the argument t in u(t) is less than zero then the unit step function is zero and when the argument t in u(t) is greater than or equal to zero then the unit step function is unity
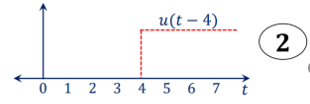
Similarly, for a shifted unit step function u(t-a) is zero if the argument (t-a) <0 or t<a and is one of the argument (t-a) > 0 or t>a.
That is
u(t-a) = 1 for t>a
=0 for t<a
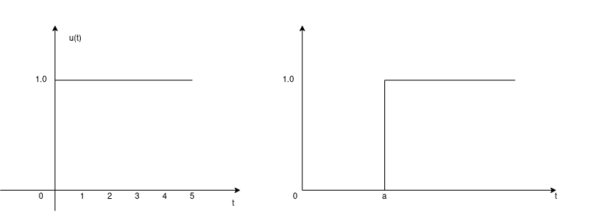
Figure 6. Unit step function
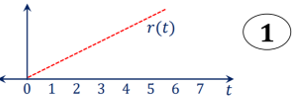
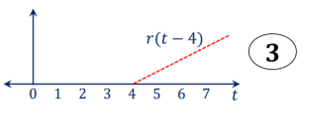
Unit ramp function
The unit ramp function is defined as:
r(t) = t for t 
=0 for t<0
Or
r(t) = t u(t)
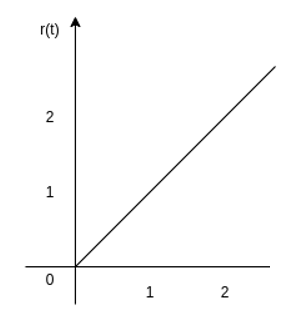
Figure 7. Unit ramp function
The ramp function can be obtained by applying the unit step function to an integrator.
r(t) = 
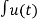dt =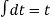 
( in the time interval t>0)
The unit step function can be obtained by differentiating the unit ramp function
Thus
u(t) = d/dt r(t)
Unit parabolic function
The unit parabolic function is given by
p(t) = t 2 / 2 for t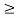 
0
= 0 for t<0
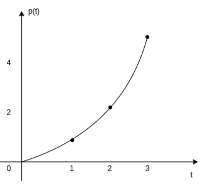
Figure 8. Unit parabolic function
Or
p(t) = t2/2 u(t)
Impulse function
The impulse function occupies an important place in signal analysis. It is defined as
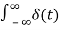dt =1
And
δ(t) =0 for t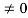
The impulse function has zero amplitude everywhere except at t=0. At t=0 the amplitude is infinity such that the area under the curve is equal to one. The unit impulse function can be obtained by using a limiting process on the rectangular pulse as shown in the figure.
Note that the area under the rectangular pulse is equal to unity.
Figure 9. Impulse function
The rectangular pulse function of the figure can be expressed as
x(t) = 1/ ∆ [ u(t) – u(t-∆)] …………………………………..(1)
The impulse function can be obtained when the width ∆ ->0 that is
δ(t) = lim ∆-> 0 x(t)
= lim ∆-> 0 1/ ∆ [ u(t) – u(t-∆)]
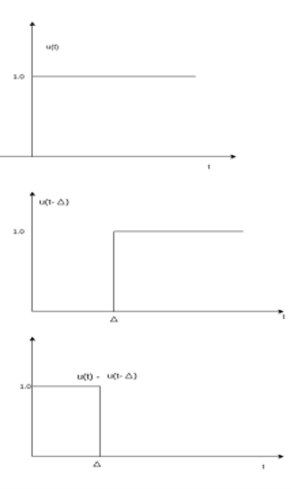
Figure 10. Unit impulse with a delay function
The delayed unit impulse function is defined as
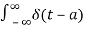=1 for t=a
And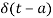 
=0 for t
a
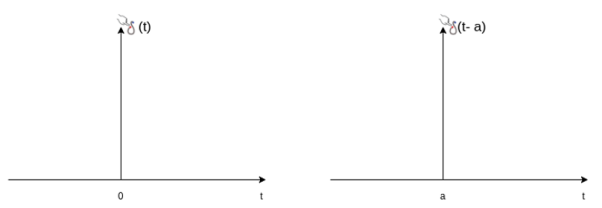
Figure 11. Impulse function
Sinusoidal signal
A continuous-time sinusoidal signal is given by
x(t) = A sin (
+ 
) ---------------------------------(1)
Where A is the amplitude, Ω is the frequency in radians per second, and 
is the phase angle in radians.
The figure shows the waveform of the sinusoidal signal with A=1, 
= -π/3 with period 2π/Ω.
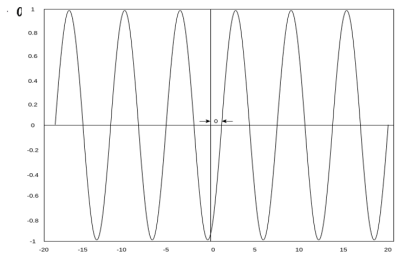
Figure 12. Sinusoidal function
Real exponential and complex exponential
Real exponential
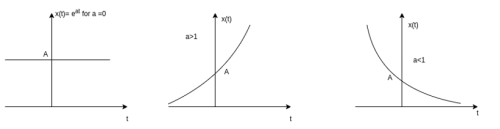
Figure 13. Real exponential function
A real exponential signal is defined as
x(t) = A e at --------------------------------(1)
Where both A and a are real. Depending on the value of ‘a’ we get different signals. If ‘a’ is positive the signal x(t) is growing exponential as shown in fig(b) If ‘a’ is negative then x(t) is decaying exponential as shown in fig(c). For a=0 x(t) is constant.
Complex exponential signal.
The most general for of complex exponential signal is given by
x(t) = e st ---------------------------------------(1)
Where s is a complex variable defined as
s =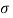 
+ j Ω
Therefore
x(t) = e st = e s(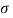
+ j Ω) = e 
t . e j Ωt
Using Euler identity, we can expand
e j Ωt = cos Ω t + j sin Ωt
Substituting in eq(1) we get
x(t) = e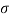 
t [ cos Ω t + j sin Ω t]
Depending on the values of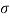 
and Ω we get different signals.
- If
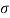=0 and Ω =0 x(t) = 1 that is the signal x(t) is a pure DC signal. - If Ω=0 then s =
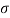, x(t) = e 
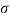t which decays exponentially for 
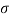<0 and grows exponentially for 
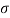> 0. - If
=0 then s=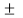 
jΩ gives x(t) = e j Ωt a sinusoidal signal with ɸ=0 - If
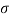<0 with finite Ω we get an exponentially decaying sinusoidal signal. - If
0 with finite Ω we get an exponentially growing sinusoidal signal.
Figure 14. Exponential function for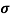 
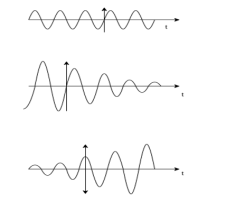
Figure 15. Complex exponential function
Rectangular Pulse:
The rectangular pulse function is defined as
Figure 16. Rectangular pulse
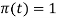for |t| 
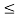½
=0 otherwise
Triangular pulse function
The unit triangular function is defined as
∆a(t) = 1 - |t|/a |t|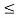 
a
0 |t| 
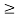a
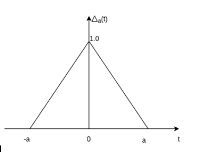
Figure 17. Triangular pulse
Signum function
The sinc function is defined by the expression
Sinc(t) = sin t/t -∞ < t < ∞
Figure 18. Signum function
The sinc function oscillates with period 2π and decays with increasing t. Its value is zero at nπ, n = ±1, ±2, …………………….. It is an even function of t.
Gaussian function:
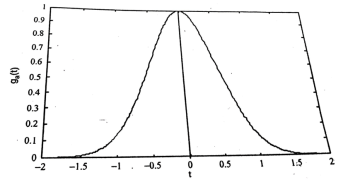
Figure 19. Gaussian function
The Gaussian function is defined by the expression
Ga(t) = e – at ^2 - ∞ <t<∞
This function is extensively used in probability theory.
Problems:
Sketch the continuous-time signal x(t) = 2 sin πt for interval 0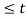
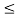2. Sample the continuous-time signal with a sampling period T =0.2 sec and sketch the discrete-time signal.
Solution:
Given:
x(t) = 2 sin πt
To sketch the signal we have values x(t) for different values of t, that is
x(0) = 2 sin π (0) = 0.
x(0.25) = 2 sin π (0.25) = √2
x(0.5) = 2 sin π (0.5) = 2
x(0.75) = 2 sin π (0.75) = √2.
x(1) = 2 sin π (1) = 0
x(1.25) = 2 sin π (1.25 = -√2
x(1.5) = 2 sin π (1.5) = -2.
x(0.25) = 2 sin π (1.75) = - √2
x(2) = 2 sin 2π =0
Take t on x-axis and x(t) on y-axis. Mark the above points and join all the points by a smooth curve to get continuous signal as shown in fig (a) . Given sampling period T =0.2
Sketch the signal x(t) = e -t for an interval 0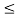
t 
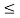2
Sample the signal with a sampling period T=0.2 second and sketch the discrete time signal.
Solution:
Given
x(t) = e -t ; x(0) =1; x(0.5) = 0.606, x(1)= 0.36768; x(1.5) = 0.2237, x(2) = 0.1353
To get signal x(t) mark the above points and draw a smooth curve joining all points as shown in figure (a)
x(nT) = x(t) | t =nT
= x(t) | t=0.2n
x(0.2n) = e -0.2 n
x(0) =1
x(1) = e – 0.2 = 0.818
x(2) = e – 0.4 = 0.67
x(3) = e – 0.6 = 0.5488
x(2) = e – 0.8 = 0.449
x(2) = e – 1 = 0.3678
x(2) = e – 1.2 = 0.3012
x(2) = e – 1.4 = 0.2466
x(2) = e – 1.6 = 0.2022
x(2) = e – 1.8 = 0.1653
x(2) = e – 2 = 0.1353
Evaluate the following integrals:
(i)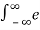 
– αt 2 δ(t-10) dt
Sol:
Given
(i)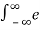 
– αt 2 δ(t-10) dt
From the property
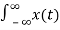δ(t-to) dt = x(to)
We have
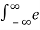– αt 2 δ(t-10) dt = e – αt2 |t=10
e-100 α
δ(t-10) =1 for t=10
= 0 otherwise
Given
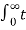2 δ(t-3) dt = t 2 | t=3 =9
δ(t-3) = 1 for t=3
=0 otherwise
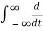δ(t) x(t) dt = -dx/dt(0)
Let u=x(t)
Dv = d/dt δ(t)
v = δ(t)
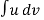= uv - 
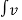du
Du = dx/dt
δ(t) x(t) dt = x(t) δ(t) | -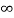
∞ - 
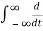x(t) δ(t) dt = - dx/dt (0)
- Elementary Discrete-Time Signals
Unit step sequence:
The unit step sequence is defined as:
u(n) = 1 for n 
=0 for n<0
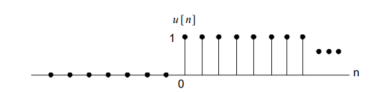
Figure 20. Unit step in discrete
Unit ramp sequence:
The unit ramp sequence is defined as
r(n) = n for n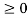 
=0 for n<0
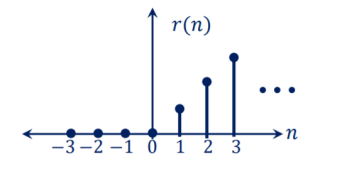
Figure 21. Unit ramp sequence
Unit sample sequence
The unit sample sequence is defined as
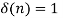for n=0
=0 for n 
0
The graphical representation of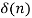 
is shown in the figure.
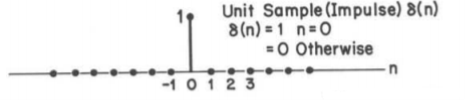
Figure 22. Unit sample sequence
The unit impulse function has the following properties:
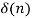= u(n) – u(n-1)
u(n) =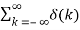 
= 
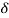(n-no) = x(no)
Exponential sequence
The exponential sequence is a sequence of the form
x(n) = a n for all n.
The figure illustrates the different types of discrete-time exponential signals. When the value of α > 1 the sequence grows exponentially and when the value is 0<a<1 the sequence decay exponentially.
When a<0 the discrete-time signal takes alternating signs.
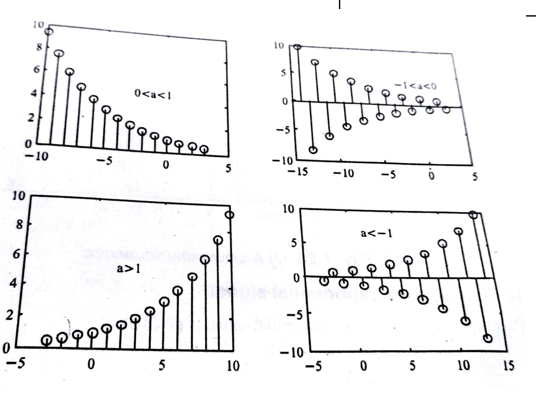
Figure 23. Exponential sequence
Sinusoidal signal
The discrete-time sinusoidal signal is given by
x(n)= A cos (won + ɸ)---------------------------(1)
Where wo is the frequency and ɸ is the phase
Using Euler’s identity we can write
A cos(won + ɸ) = A/2 e jɸ . e j won + A/2 e-jɸ e -jwon ---------------------(2)
Since | e jwon | 2 =1
The energy of the signal is infinite and the average power of the signal is 1.
An example of a discrete-time sinusoidal signal is shown in the figure.
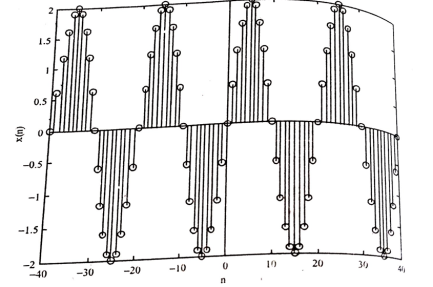
Figure 24. Sinusoidal sequence
Complex exponential signals
The discrete time complex exponential signal is given by
x(n) = a n e j (won + ɸ) ------------------------------------(1)
= a n cos (wo + ɸ) + j a n sin (won + ɸ) .
For |a| =1 the real and imaginary parts of the complex exponential sequence are sinusoidal.
For |a| < 1 the amplitude of sinusoidal sequence decays exponentially
For |a| > 1 the amplitude of the sinusoidal sequences increases exponentially. Examples of these signals are given in the figure.
Figure 25. Complex exponential sequence
Deterministic
A signal is said to be deterministic if there is no uncertainty with respect to its value at any instant of time or the signals which can be defined exactly by a mathematical formula are known as deterministic signals.
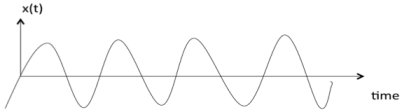
Figure 26. Deterministic signal
Random
A signal is said to be non-deterministic if there is uncertainty with respect to its value at some instant in time. Non-deterministic signals are random in nature hence they are called random signals. Random signals cannot be described by a mathematical equation. They are modeled in probabilistic terms.
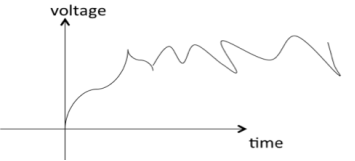
Figure 27. Random signal
Periodic
A signal is said to be periodic if it satisfies the condition x(t) = x(t + T) or x(n) = x(n + N).
Where
T = fundamental time period,
1/T = f = fundamental frequency.
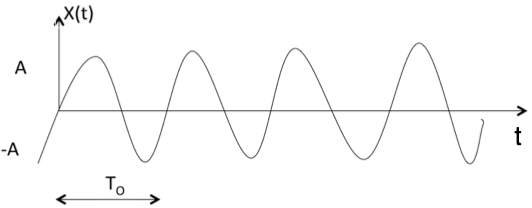
Figure 28. Random signal
The above signal will repeat for every time interval T0 hence it is periodic with period T0.
Non-periodic
Non-periodic signals (also known as aperiodic signals), unlike periodic signals, do not have just one particular frequency. Instead, they are spread out over a continuous range of frequencies. For example, a speech signal
Energy
A signal is said to be an energy signal when it has finite energy
Energy E =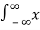 
2(t) dt
Power:
A signal is said to be a power signal when it has finite power.
Power P = lim T-> ∞ 1/2T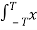 
2 (t) dt
Even and odd signal.
A signal is said to be even when it satisfies the condition x(t) = x(-t)
Example 1: t2, t4… cost, etc.
Let x(t) = t2
x(-t) = (-t)2 = t2 = x(t)
∴,∴, t2 is even function
Example 2: As shown in the following diagram, rectangle function x(t) = x(-t) so it is also even function.
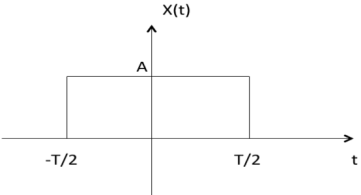
Figure 29. Even signal
A signal is said to be odd when it satisfies the condition x(t) = -x(-t)
Example: t, t3 ... And sin t
Let x(t) = sin t
x(-t) = sin(-t) = -sin t = -x(t)
∴,∴, sin t is odd function.
Any function ƒ(t) can be expressed as the sum of its even function ƒe(t) and odd function ƒo(t).
ƒ(t ) = ƒe(t ) + ƒ0(t )
Where
ƒe(t ) = ½[ƒ(t ) +ƒ(-t )]
Time Shifting
Let us consider a signal x(t) as shown in the figure. The time-shifting of x(t) may delay or advance the signal in time. Mathematically this can be represented by
y(t) = x(t-T) ------------------------------------------(1)
If T is positive the shifting delays the signal as shown in the figure.
If T is negative the shifting advances the signal as shown in the figure.
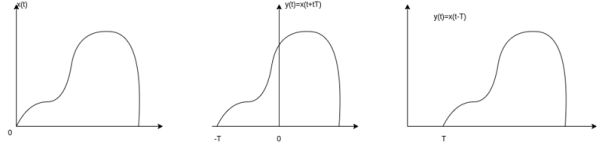
Figure 30. Time Shifting
Similarly, the time-shifting operation of discrete-time signals is represented by
y(n) = x(n-k)
Which shows that the signal y(n) can be obtained by shifting x(n) by k units. If k is positive the shift is to the right (delay) and if k is negative the shift is to the left. Let us consider a signal x(n) as shown in the figure. The signal x(n-2) is obtained by shifting x(n-2) is obtained by shifting x(n) right by 2 units of time. The result is shown in fig (b). On the other hand x(n+3) is obtained by shifting x(n) left by three units of time.
Figure 31. Time-shifting in discrete time
Time Reversal
The time-reversal of signal x(t) can be obtained by folding the signal about t=0. It is denoted by x(-t). The signal x1(t) and its reflection x(-t) are illustrated in fig a and b respectively.
Figure 32. Time Reversal
The signal x(-t+2) is obtained by delaying x1(-t) by two units of time and x1(-t-2) is obtained by advancing x1(-t) by two units of time. The signals x1(-t+2) and x1(-t-2) are shown in figure ( c) and (d).
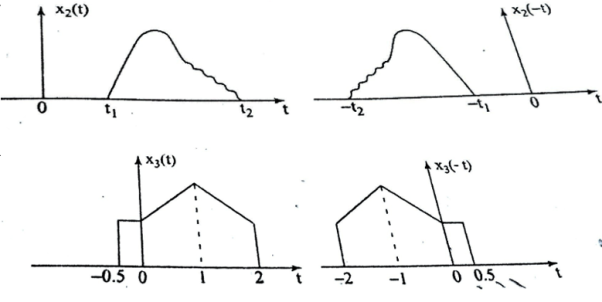
Figure 33. Operation on time reversal
The time-reversal of the discrete-time signal can be obtained by folding the sequence x(n) about n=0. For signal x1(n) in fig, the time-reversal signal x1(-n) is shown in fig (b).
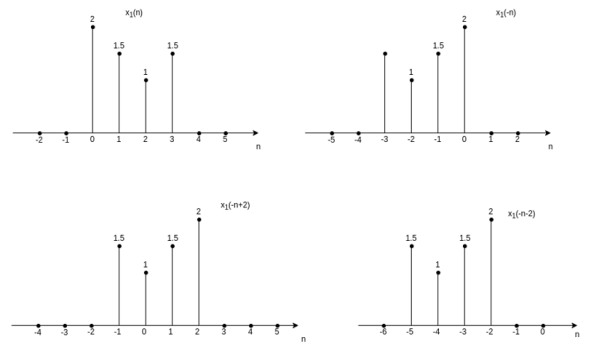
Figure 34. Operation of time reversal in discrete
The signal x1(-n+2) is obtained by delaying x1(-n) by two units of time and x1(-n-2) is obtained by advancing x1(-n) by two units of time. The other examples for time-reversal of the discrete-time signal are obtained by fig (a) and (b).
Figure 35. Input and output signal
Problem:
Sketch the following signals
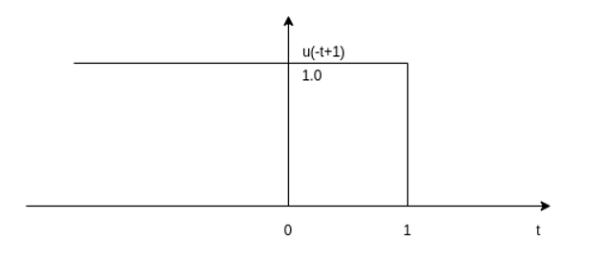
(i) u(-t+1)
Step 1: draw the unit step signal
Step 2: Fold the signal about t-0 as shown in fig (b)
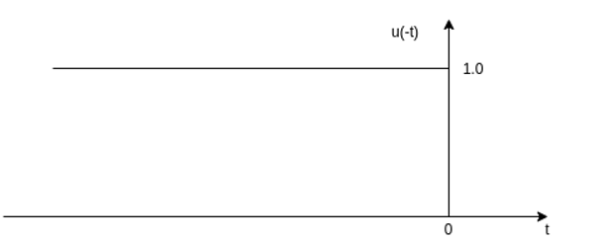
Step 3: Shift the signal u(-t) right by one unit as shown in fig(c )
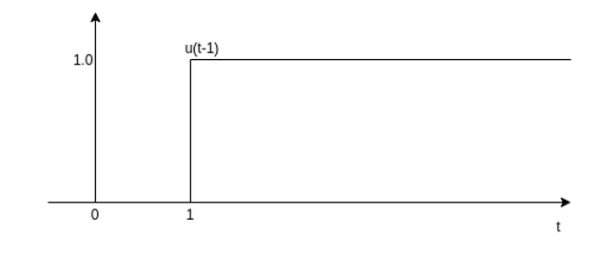
(ii) x(t) = -2 u(t-1)
Step 1: Draw the unit step signal
Step 2: Shift the signal u(t) right by one unit of time as shown in the figure.
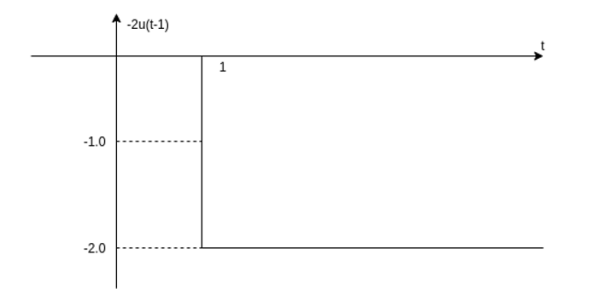
Step3: Multiply the signal u(t-1) with -2
Amplitude Scaling:
Consider a signal x(t) that is fed to an amplifier with a gain of 3 then the output of an amplifier can be represented by
y(t) = 3 x(t)
That is the output y(t) is identical in shape to the input signal x(t) but its amplitude is thrice everywhere. This concept is illustrated in the figure.
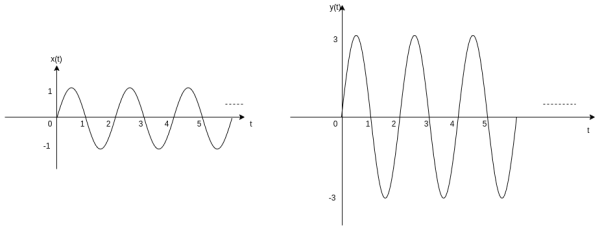
Figure 36. Amplitude Scaling
From fig we find that the amplitude is rescaled hence the name amplitude scaling.
Similarly, the amplitude scaling of a discrete-time signal can be represented by
y(n) = a x(n)
If x(n) is as shown in figure and a=2 then y(n) is as shown in figure(b).
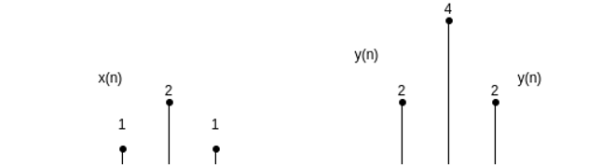
Figure 37. Amplitude scaling in discrete
Time scaling:
Let us consider a signal x(t) as shown in figure(a). The time scaling of the signal can be accomplished by replacing t by at in signal x(t).
If a=2 we get new signal
y(t) = x(2t)
Observe that x(t) is switching from 0 to 1 at t=-1 and switching from 1 to 0 at t=3. . When y(t) = 2t, y(t) = x(2t), y(t) switches from 0 to 1 at t=0.5 and switches from 1 to 0 at t=1.5.
In the original signal x(t) magnitude is equal to 1 at t=0 and t=2. But in a time-scaled signal y(t) magnitude is equal to 1 at t=0 and t=2. But in a time-scaled signal y(t) magnitude is equal to 1 at t=0 and t=1. This behavior shows that x(t) is compressed in time by factor 2.
Figure 38. Time Scaling
The resulting signal x(2t) is shown in fig(b). Let x(t) be an audio signal. If x(t) were recorded on a magnetic tape then x(2t) is the signal played back twice the recording speed.
Now consider another signal y(t) = x(at) with a=1/2. Figure ( c ) shows x(1/2) which is expanded in time by factor 2.
In discrete- time signal
y(n) = x(2n)
Let x(n) be a sequence as shown in figure. Then we plot time scaled signal y(n) by substituting different values of n.
For n =-1
y(-1) = x(-2) =2
…..
y(0) = x(0) =4
y(1) = x(2) =2
y(2) = x(4) = 0
Figure 39. Time scaling in discrete
Signal addition:
The sum of two continuous-time signals can be obtained by adding their values at every instant. Similarly, the subtractions of two continuous-time signals can be obtained by subtracting their values at every instant.
Figure 40. Signal addition
Let us consider the addition and subtraction of two signals x1(t) and x2(t) as shown in Figures (a) and (b).
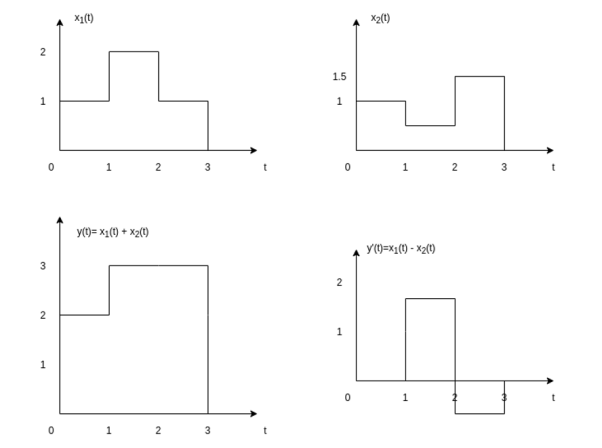
Figure 41. Addition and Subtraction of signal
The addition of signals of two signals x1(t) and x2(t) can be obtained by considering each time interval separately as follows:
x1(t) = 1 for 0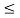 
t 
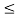1 and
x2(t) =1 for 0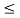 
t 
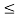1
Hence x1(t) + x2(t) = 2 for 0 
t 
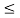1
x1(t) = 2 for 1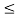 
t 
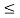2 and
x2(t) =0.5 for 1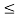 
t 
2
Hence x1(t) + x2(t) = 2.5 for 1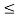 
t 
2
x1(t) = 1 for 2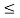 
t 
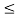3 and
x2(t) =1.5 for 2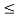
t 
3
Hence x1(t) + x2(t) = 2.5 for 2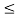 
t 
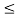3
The sketch for y(t) = x1(t) + x2(t) as shown in fig ( c )
In the same way the subtraction of x2(t) from x1(t) can be obtained. By inspection we can find
y’(t) = x1(t) – x2(t) = 0 for 0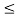 
t 
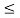1
= 1.5 for 1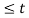 
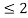
= -0.5 for 2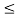 
t 
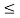3
For discrete-time signals, the sum of two sequences can be obtained by adding the sequence values at the same index n for which the sequences are defined.
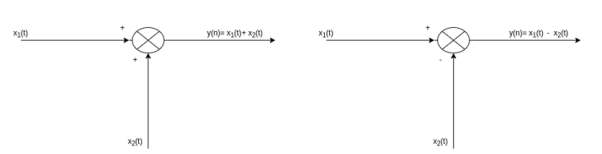
Figure 42. Addition of signal in discrete time
If x1(n) = {1, 3, 2, 1} and
x2(n) = {1, -2, 3, 2}
Then
x1(n) + x2(n) = { 1+1, 3-2, 2+3, 1+2}= {2, 1, 5, 3}
x1(n) – x2(n) = { 1-1, 3-(-2), 2-3, 1-2} = { 0, 5, -1, -1}
Signal Subtraction
The subtraction of two signals is nothing but a subtraction of their corresponding amplitudes.
Consider the following example:
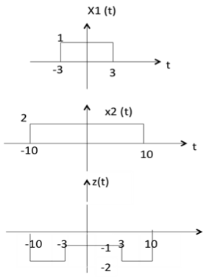
Figure 43. Subtraction of signal in discrete
As seen from the diagram above,
-10 < t < -3 amplitude of z (t) = x1(t) - x2(t) = 0 - 2 = -2
-3 < t < 3 amplitude of z (t) = x1(t) - x2(t) = 1 - 2 = -1
3 < t < 10 amplitude of z (t) = x1(t) + x2(t) = 0 - 2 = -2
Signal multiplication
The multiplication of two signals can be obtained by multiplying their values at every instant.
The multiplication process is illustrated in the figure.
In the interval 0 
t 
1
x1(t) = t; x2(t) = 1. Therefore y(t) = x1(t) x2(t)
Therefore y(t) = x1(t) x2(t)=t
In in the interval 1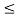 
t 
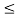2
x1(t) =1; x2(t) = 0.5. Therefore y(t) = 0.5
In in the interval 2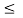 
t 
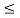3
x1(t) =0.5; x2(t) = 1.5. Therefore y(t) = 0.75
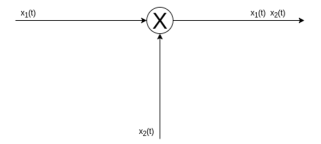
Figure 44. Signal multiplication
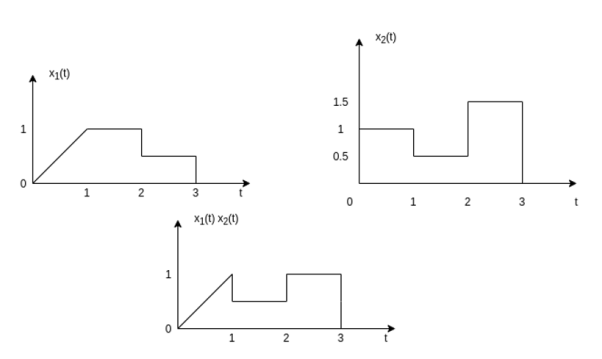
Figure 45. Multiplication of x1 and x2
Figure 46. Multiplication of signal in discrete
If x1(n) = { 1, 2, -2, 3} and x2(n) = {1, 0.5, 0.5, 1} then
y(n) = x1(n) . x2(n) ={ 1.1, 2.(0.5), -2(0.5), 3.1}
={1, 1, -1, 3}
Problem:
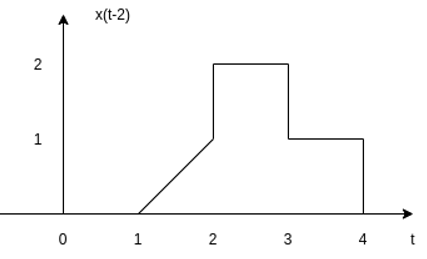
For the signal x(t) as shown in figure find:
(i) x(t-2)
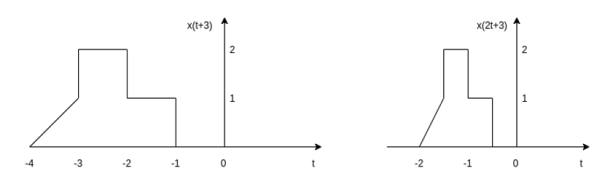
(ii) x(2t +3)
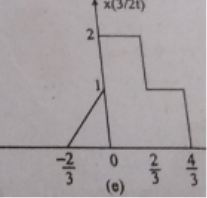
(iii) x(3/2t)
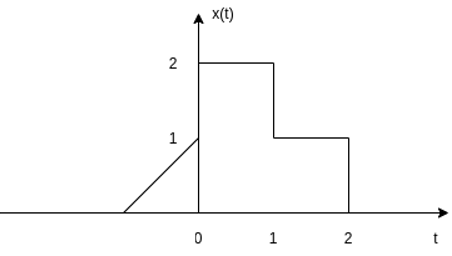
x(t-2)
This signal can be obtained by delaying the signal by 2 units of time.
x(2t+3)
This signal can be obtained first shifting the sequence x(t) left by 3 units of time as shown in fig and then by applying time scaling by factor 2. The resultant signal is shown in the figure.
x(3/2t)
The signal x(3/2t) can be obtained by compressing the signal x(t) by 2/3 times.
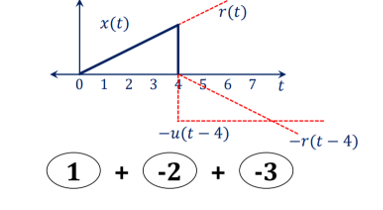
Express the following:
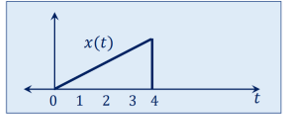
x(t) = r(t) – [ u(t-4) + r(t-4)]
A system is defined as a physical device that generates a response or output signal for the given input signal.
The relation between input and output is denoted as
y(t) operation on x(t)
Figure 47. System
Mathematically
y(t )= T[x(t)]
Where input x(t) is transformed to y(t).
Static and Dynamic systems
A system is static or memoryless if its output at any instant of time depends on the input at that instant of time but not on the past or future values of input. Otherwise, the system is dynamic or with memory.
Examples
y(t) = x 2 (t) in continuous time Static or memory less
y(n) = n x(n) in discrete time system
Find whether the following systems are dynamic or not:
a) y(t) = x(t-2)
Here, the output depends on the past value of input therefore the system is dynamic
b) y(n) = x(n+2)
The output depends on the future value of the input. Therefore, the system is dynamic.
c) y(t) = x2(t)
The output depends on the present input. Therefore, the system is static.
Casual and Non-casual systems
A causal system is one for which the output at any time depends on the present and past inputs but not future inputs These systems are known as non- anticipative systems.
A non-casual system is one whose output depends on future values.
Examples of casual system:
y(t) = x(t) + x(t-1)
y(n) = n x(n) + x(n-3)
Examples of non-casual system
y(t) = x(t+3) + x 2 (t)
y(n) = x(2n)
For example
y(t) = 2 x(t) + 3 x(t-3)
Let t=1 therefore y (1) = 2 x(1) + 3 x(-2)
The system output only depends upon present and past inputs. Hence, the system is causal.
y(t) = 2 x(t) + 3 x(t – 3) + 6 x( t+3)
Let t=1 the system output is
y(1) = 2x(1) + 3 x(-2) + 6 x( 4)
Here the output depends future input. Hence non –casual.
Linear and Non-linear systems
The superposition principle states that the response to a weighted sum of input signals be equal to the weighted sum of the outputs corresponding to each of the individual input signals. A system that satisfies the superposition principle is said to be the linear system.
T [a1 x1(t) + a2 x2(t)] = a1 T[x1(t)] + a2 T[x2(t)]
∴, T [a1 x1(t) + a2 x2(t)] = a1 y1(t) + a2 y2(t)
Similarly, for discrete –time linear system
T [ax1(n) + bx2(n)] = a T[x1(n) + bTx2(n)]
Example:
Check whether the systems are linear or not.
a) dy/dt + 3t y(t) = t2 x(t)
b) y(t) =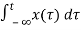 
c) y(n) = Ax(n) + B
Solution:
a) dy/dt + 3t y(t) = t2 x(t)
For input x1(t) the output is y1(t)
dy1(t)/dt + 3t y1(t) = t2 x1(t) --------- (1)
Similarly, for x2(t) output is y2(t)
Dy2(t)/dt + 3t y2(t) = t2 x2(t) ---------- (2)
Multiply (1) with a and (2) with b
a dy1(t) /dt + 3at y1(t) + b dy2(t)/dt + 3by2(t) = at2 x1(t) + bt2 x2(t)
d/dt[ay1(t) +by2(t)] + 3t[ay1(t) + by2(t)] = t2[ax1(t) + bx2(t)]
The system is linear because weighted sum of inputs produces the corresponding weighted sum of outputs.
b) y(t) =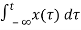 
For x1 input output is y1(t)
y1(t) =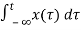
y2((t)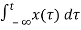 
Linear combination of both yields
Therefore, system is linear.
c) y(n) = Ax(n) + B
For input x1(n) the corresponding output is y1(n)
y1(n) = T[x1(n)] = Ax1(n) + B; y2(n) = Tx2(n)] = A x2(n) + B
Ay1(n) + by2(n) = a[Ax1(n) + B] + b[Ax2(n) +B]
The output will be y3(n) = A[x1(n) + x2(n)] +B
y3(n) ≠ ay1(n) + by2(n)
Therefore, system is non-linear.
d) y(t) = e x(t)
y1(t) = e x1(t)
y2(t) = e x2(t)
y3(t) = T[ax1(t) + b x2(t)] = e[ax1(t)+bx2(t)]
Ay1(t) + by2(t) = a ex1(t) + b ex2(t)
y3(t) ≠ ay1(t) + b y2(t)
Hence, system is not linear.
Time-Variant and Time-invariant systems
A system is said to be time-variant if its input-output characteristics do not change with time.
Suppose we apply a signal(t) to a system to a system and obtain an output y(t) as shown in the figure.
If we delay by T seconds then for a time-invariant system the output will be delayed by T seconds.
Example
Determine whether the following systems are time variant or time invariant.
a) y(t) = x(t) cos 50πt
b) y(t) = e x(t)
c) y(t) = x(t2)
d) y(n) = x2(n-1)
Sol:
a) y(t) = x(t) cos 50πt
If the input is delayed by T sec then output
y(t, T) = T[x(t-T)] = x(t-T) cos (50πt)
If the output is delayed by T sec then
y(t-T) = x(t-T) cos 50 π(t –T)
y(t, T) ≠ y(t – T)
Hence the system is time-variant.
b) y(t) = ex(t)
The output for delayed input is
y(t, T) = e x(t-T)
The delayed output is
y(t-T) = ex(t-T)
y (t, T) = y(t-T)
Hence, system is time-invariant.
c) y(t) = x(t2)
The output for delayed input is
y(t, T) = x (t2 –T)
The delayed output is
y(t-T) = x(t-T)2
y(t, T) ≠ y(t – T)
Hence the system is a time variant
d) y(n) = x2 (n-1)
The output for delayed input is
y(n-k) = x2(n-1-k)
The delayed output is
y(n-k) = x2 (n-1-k)
y(n, k) = y(n-k)
System is time invariant.
Stable and unstable systems
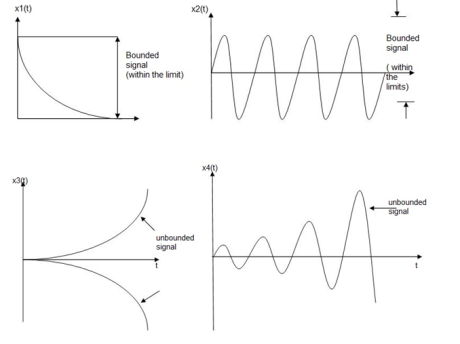
Figure 48. Stable and unstable systems
An input signal x(t) is said to be bounded if it satisfies the condition |x(t) |≤Mx < ∞ for all t.
Similarly, the output signal is bounded if it satisfies the condition |y(t)| ≤My < ∞
The example for bounded and unbounded signals is as shown in the figure.
Note: For a bounded signal, the amplitude is finite.
Example 1: y (t) = x2(t)
Let the input is u(t) that is unit step then output y(t) = u2(t) = u(t) = bounded output.
Hence, the system is stable.
Example 2: y (t) = ∫x(t)dt∫x(t)dt
Let the input be u (t) then
Output y(t) = ∫u(t)dt but ∫ u(t)dt = ramp signal
It is unbounded because the amplitude of ramp is not finite and tends to become infinite when t →infinite
Hence, the system is unstable.
Check whether the following systems are
Static or dynamic
Linear or Non-linear
Causal or non-casual
Time-Invariant or time-variant
Sol:
a) y(t) d2y(t) /dt2 + 3t dy(t)/dt + y(t) = x(t)
- Since it is a differential equation the system is dynamic.
- The input x1(t) and output y1(t) can be described by
y1(t) d2 y1(t)/dt2 + 3t dy1(t)/dt + y1(t) = x1(t)
Similarly, y2(t) d2y2(t)/dt2 + 3t dy2(t)/dt + y2(t) =x2(t)
a y1(t) d2y1(t)/dt2 + 3at dy1(t)/dt + a y1(t) + b y2(t) d2y1(t)/dt2 + 3bt dy1(t)/dt +by2(t) = ax1(t) + b x2(t)
Ay1 d2 y1(t)/dt2 + by2(t) d2 y(t)/dt2 + 3t d/dt[ay1(t) + b2 y2(t)] + ay1(t) + b y2(t) = ax1(t) + bx2(t)
Since the differentiation ay1(t) d2 y1(t)/dt2 + by2(t) d2 y2(t)/dt2 is not a function of the weighted sum of outputs, superposition principle is not satisfied hence the system is non-linear.
- The output depends on the present input only hence the system is causal.
- The co-efficient of the differential equations is a function of time. Hence the system is time-variant.
y(n) = x(n) x(n-1)
The output depends on the past values of input. Hence it requires memory therefore the system is dynamic.
The output y1(n) for input x1(n) is
y1(n) = x1(n) x1(n-1)
y2(n) = x2(n) x2(n-1)
y3(n) = ax1(n) + b x2(n) [ax1(n-1) + b x2(n-1)]
a y1(n) + by2(n) = a x1(n) x1(n-1) + bx2(n) x2(n-1)
Since y3(n) ≠ ay1(n) + b y2(n)
Hence the system is non-linear.
The output depends on the present and past values of input. Hence the system is casual.
y(n) = x(n) x(n-1)
y (n, k) = x(n-k) x(n-1-k)
y(n-k) = x(n-k) x(n-1-k)
Since y(n, k) = y(n-k) the system is time-invariant.
b) y (n) = cos[x(n)]
The output depends on the input at that instant. Therefore, system is static.
For input x1(n)
y1(n) = cos[x1(n)]
For input x2(n)
y2(n) = cos[x2(n)]
y3(n) = cos[ax1(n)+ b x2(n)]
a y1(n) + b y2(n) = a cos [x1(n)] + b cos[x2(n)]
Hence the system is non-linear.
The output depends on the present input hence the system is casual.
y(n) = cos[x(n)]
y(n, k) = cos[x(n-k)]
y(n-k) = cos[x(n-k)]
y(n, k) = y(n-k)
Hence system is time –invariant.
For the given system check whether the system is linear, time-invariant, casual memoryless, or stable.
y(t) = x(t-2) + x(2-t)
- The system is not memoryless since the output depends on the past and future values of input.
- The system is non-casual since output depends on the future values of input.
y (t, 
= x1(t-2-
)+x1(2-t-
)
y(t-
) = x(t-2-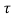
) + x2(2-t+
)
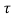y (t,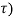 
≠ y (t-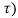
System is time variant.
y1(t) = x1(t-2) + x1(2-t)
y2(t) = x2(t-2) + x2(2-t)
a1y1(t) + a2 y2(t) = a1 x1(t-2)+ a1x1(2-t) + a2x2(t-2)+a2x2(2-t)
= a1x1(t-2) + ax2(t-2) +a1x1(2-t)+a2 x2(2-t)
= System is linear.
For bounded input, the output is also bounded. Hence the system is stable.
References:
1. Haykin. S., Venn B. V. Signals and Systems
2. Oppenheim A.V., Willsky A.S. &Nawab S.H., Signals and Systems, Tata McGraw Hill
3. Taylor F.H, Principles of Signals and Systems, McGraw Hill
4. Bracewell R.N., Fourier Transform & Its Applications, McGraw Hill
5. Haykin S., Communication Systems, John Wiley
