Unit – 1
Function of one variable
It is the process of differentiating the given function simultaneously many times and the result obtained are called successive derivative.
Let 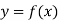 be a differentiable function.
be a differentiable function.
First derivative is denoted by 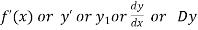
Second derivative is 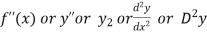
Third derivative is 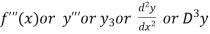
Similarly the nth derivative is 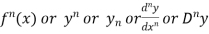
Successive differentiation-
The successive differential coefficients of y are denoted as follows-
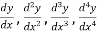 ……………….
……………….
The 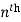 differential coefficient is-
differential coefficient is- 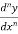
Other notations to denote n’th differential coefficients-
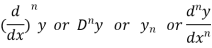
The process of applying differentiation again and again is called successive differentiation.
nth derivative of standard functions-
1. nth derivative of 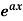 –
–
Suppose y = 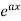 ,
,
Differentiate with respect to x successively, we get
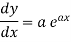
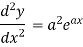
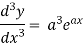
For n times differentiation, we get-
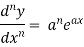
So we can say that its n’th derivative will be
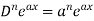
2. nth derivative of log(ax + b)-
Suppose y = log (ax + b)
Differentiate with respect to x successively, we get
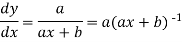
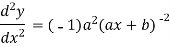
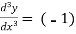 (-2)
(-2) 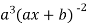
For n times differentiation, we get-
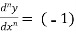 (-2)…………….(-n + 1)
(-2)…………….(-n + 1) 
= 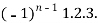 …………….(n - 1)
…………….(n - 1) 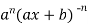
= 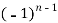 (n - 1)
(n - 1)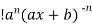
So we can say that its n’th derivative will be
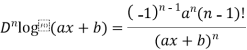
3. nth derivative of 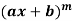
Suppose y = 
Differentiate with respect to x successively, we get
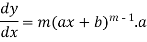
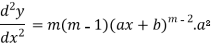
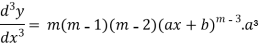
For n times differentiation, we get-
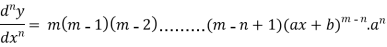
So we can say that its n’th derivative will be
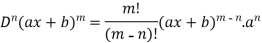
4. nth derivative of sin(ax + b)-
Suppose y = sin(ax + b)
Differentiate with respect to x successively, we get
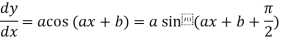
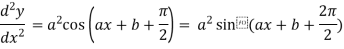
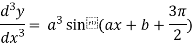
For n times differentiation, we get-
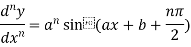
So we can say that its n’th derivative will be

5. Nth derivative of 
Let us consider the functions-
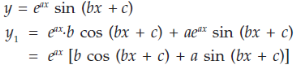
To rewrite this in the form of sin, put-
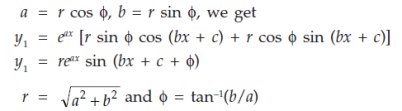
Diff. Again w.r.t.x, we get-
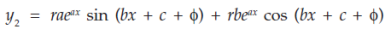
Substitute for a and b, we get-
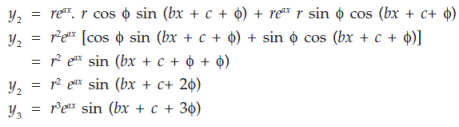
…………………………………………………………………………
Similarly we get-
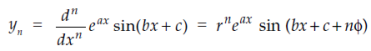
And
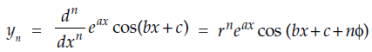
Similarly we can find the ‘n’ derivatives of such functions-
Standard results-
1.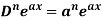
2. 
3.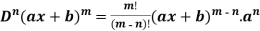
4.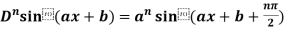
5. 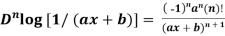
6. 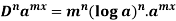
7. 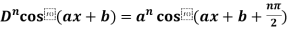
Example: If y = l , then show that-
, then show that-
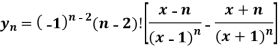
Sol. We have,
y = 
Differentiate y with respect to x, we get
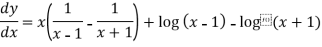
= 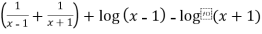
Again diff. (n – 1) times w.r .t x , we get-
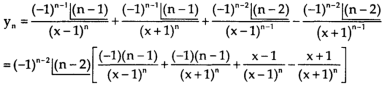

Order differential equation
N’th order differential equations can be solved as below-
Example: Find the 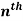 derivative of
derivative of 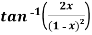
Sol. Here we have-
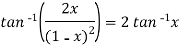
Suppose, y = 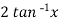
First derivative-
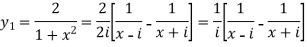
Here ,

Let x = 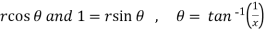
So that
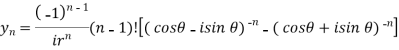
Which is the n’th derivative of the given function.
Example: Find cos x cos 2x cos 3x.
Sol.
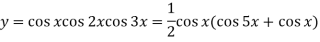
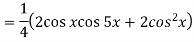
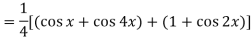

So that-
n’th derivative-
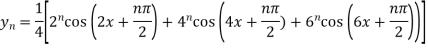
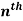 derivatives of algebraic functions,
derivatives of algebraic functions, 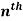 derivatives of function belongs to polar form
derivatives of function belongs to polar form
Example: Find the 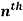 derivative of the following function-
derivative of the following function-
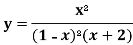
Sol. Partial fraction of the function y after splitting-
Suppose x – 1 = z, then
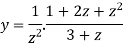
= 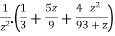
= 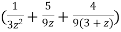
= 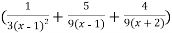
Here we can find its n’th derivative-
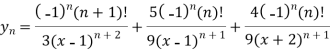
Example: Find 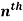 derivative of the given function:
derivative of the given function:
y = 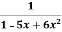
Sol. We are given-
y = 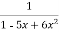
Factorize the denominator-
y = 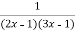
=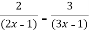
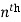 derivative will be-
derivative will be-
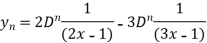
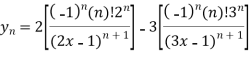
Which is the 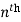 derivative of the given function.
derivative of the given function.
Example: Find 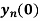 if
if 
Sol.
Here we have-
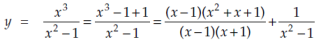

At x = 0,

When n is odd-
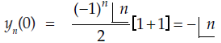
When n is even
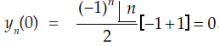
Example: Find the nth derivative of sin3 x
Sol: we know that sin 3x= 3sin x 4sin3 x = sin3x = 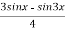
Differentiate n times w.r.t x,
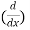 ( sin3 x) =
( sin3 x) = 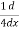 (3 sinx- sin3x)
(3 sinx- sin3x)
= ( -3n. Sin( 3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
( -3n. Sin( 3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
Example: Find the nth derivative of sin 5x. Sin 3x.?
Sol: let y = sin 5x.sin 3x=  ( sin 5x.sin 3x)
( sin 5x.sin 3x)
⇒y=  ( cos 2x - cos8x)
( cos 2x - cos8x)
⇒ y= ( cos 2x- cos8x )
( cos 2x- cos8x )
Differentiate n times w.r.t x,
Yn = 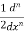 ( cos 2x - cos8x )
( cos 2x - cos8x )
⇒ yn =  ( 2 n (cos( 2x+ nπ/2)- 8n .cos (8x + nπ/2)) nϵz.
( 2 n (cos( 2x+ nπ/2)- 8n .cos (8x + nπ/2)) nϵz.
Successive n th derivative of nth elementary function ie., exponential
Example: If y = ae n x + be –nx , then show that y2= n2y
Sol: Y= aenx + be-nx
y 1 = a.n.enx - b.n.e-nx
y2 = an2 enx – bn2 e-nx = n2 (ae nx+ be –nx)
y2= n2y.
Example: If y= e-kx/2(a cosnx+ b sinnx) then show that.,y2+ ky1+(n2+ k2/4)y =0
Sol: y= e-kx/2(a cosnx+ b sinnx)
Differentiating w.r.to. x.,
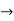 Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y
Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y
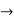 Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx)
Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx) 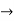 (1)
(1)
Differentiating w.r.to x.,
Y2+ k/2.y1 = ne-kx/2 (-k/2) ( -an sin nx + bn cos nx) + n e-kx/2(-an cosnx- bn sinnx).
= -(k/2) (y1+ k/2 y)- n2 y = - (k/2 y1)- ( k2/4)y- n2y.
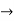 y2 + ky1 +(n2+ k2/4)y = 0.
y2 + ky1 +(n2+ k2/4)y = 0.
Key takeaways-
1.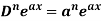
2. 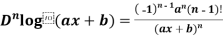
3.
4.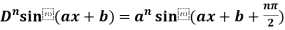
5. 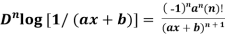
6. 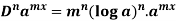
7. 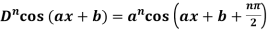
Statements of Leibnitz’s Theorem-
If u and v are the function of x such that their nth derivative exists, then the nth derivative of their product will be
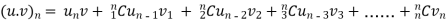
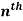 derivative of product of two functions by Leibnitz theorem-
derivative of product of two functions by Leibnitz theorem-
Example-1 If y  , then prove that-
, then prove that-
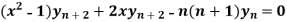
Sol. Here it is given that-
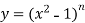
On differentiating-

Or
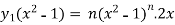
= ny.2x
Differentiate again with respect to x, we get-
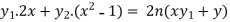
Or
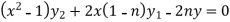 …………………. (1)
…………………. (1)
Differentiate each term of (1) by using Leibnitz’s theorem, we get-
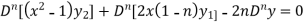
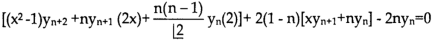
Therefore we get-
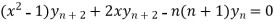
Hence proved.
Example-2: If 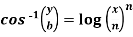 , then prove that-
, then prove that-
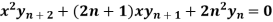
Sol. Here we have-
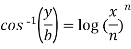
Or
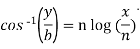
Or
y = b cos[ n log(x/n)]
On differentiating, we get-
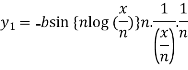
Which becomes-

Differentiate again both sides with respect to x, we get-
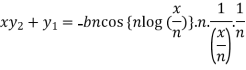
It becomes-

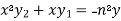
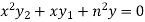 ……………….. (1)
……………….. (1)
Differentiate each term n times with respect to x, we get-
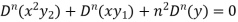
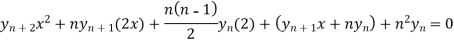
Which is-
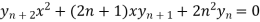
Hence proved,
Example-3: If y = 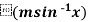 , then prove that-
, then prove that-
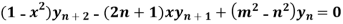
Sol. It is given that- y = 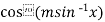
First derivative –
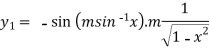
It becomes-
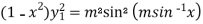
= 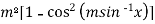
= 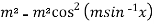
= 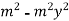
Becomes-
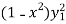 +
+  -
- 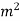 = 0
= 0
Om differentiating again we get-
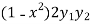 +
+ 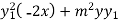 = 0
= 0
Or
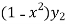 +
+ 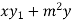 = 0
= 0
Differentiate n times by using Leibnitz’s theorem, we get-
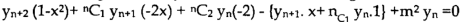
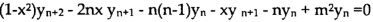
So that

Hence proved.
Example-4: Find the nth derivative of 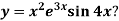
Sol.
Let 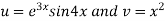
Also 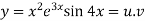
By Leibnitz’s theorem
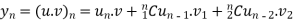
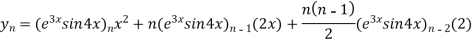
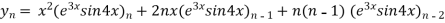 …(i)
…(i)
Here 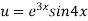
Differentiating with respect to x, we get
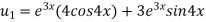
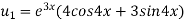
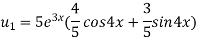
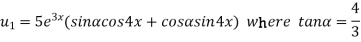
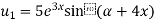
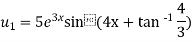
Again differentiating with respect to x, we get
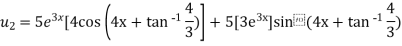
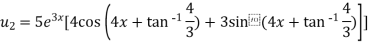

Similarly the nth derivative will be
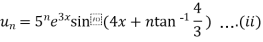
From (i) and (ii) we have,
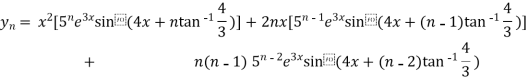
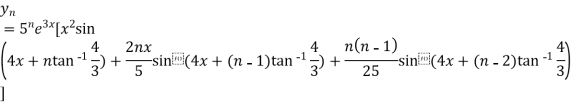
Example-5: If 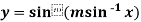 , then show that
, then show that
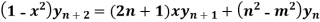
Sol.
Also, find 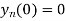
Here 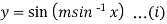
Differentiating with respect to x, we get
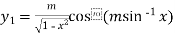 …(ii)
…(ii)

Squaring both side we get
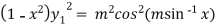
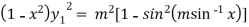

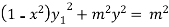 …(iii)
…(iii)
Again differentiating with respect to x ,we get
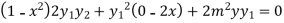

Using Leibnitz’s theorem we get
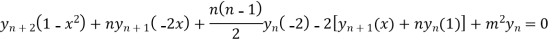
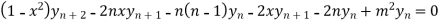
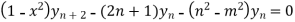 …(iv)
…(iv)
Putting x=0 in equation (i),(ii) and (iii) we get
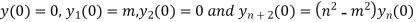
Putting n=1,2,3,4….
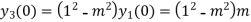
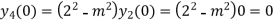

………………
Hence 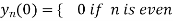
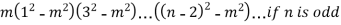
Example-6: If  then show that
then show that
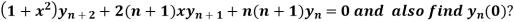
Sol.
Given 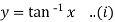
Differentiating both side with respect to x.
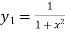 …..(ii)
…..(ii)
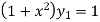
Again differentiating with respect to x, we get
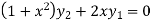 …(iii)
…(iii)
By Leibnitz’s theorem
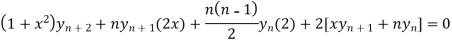
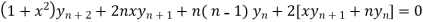
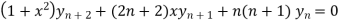
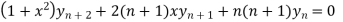 …(iv)
…(iv)
Putting x=0 in equation (i),(ii),(iii) and (iv) we get

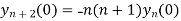
Putting n=1,2,3,4… so we get
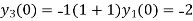
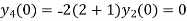

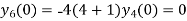
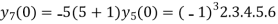
Hence we have
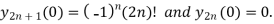
Key takeaways-
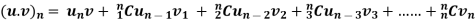
- The
 differential coefficient is-
differential coefficient is- 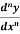
- 1.
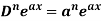
- 2.
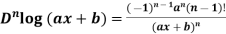
- 3.
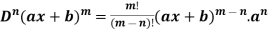
- 4.
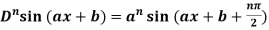
- 5.

- 6.
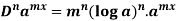
- 7.

Maclaurin’s series-
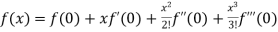 + …….
+ …….
Which is called Maclaurin’s theorem.
Note – if we put h = x - a then there will be the expansion of F(x) in powers of (x – a)
We get-
 + …….
+ …….
Expansion of functions using standard expansions-
Example: By using Maclaurin’s series expand tan x.
Sol.
Let-

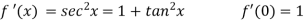
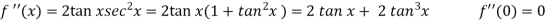
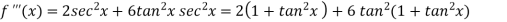

Put these values in Maclaurin’s series we get-
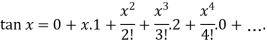
Example: Expand 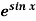 by using Maclaurin’s series.
by using Maclaurin’s series.
Sol.
Let

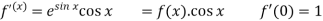
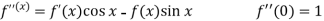
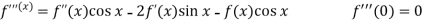
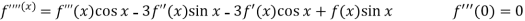
Put these values in Maclaurin’s series-
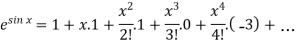
Or
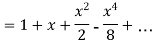
Expand by Maclaurin’s theorem,
Log sec x
Solution:
Let f(x) = log sec x
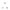 By Maclaurin’s Expansion’s,
By Maclaurin’s Expansion’s,
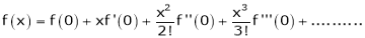 (1)
(1)
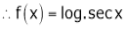
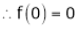

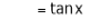
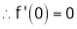
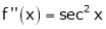
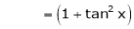
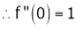

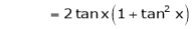
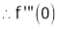

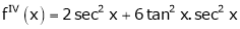
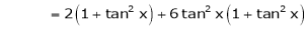
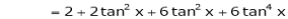

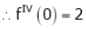
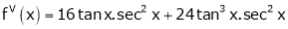
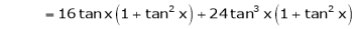
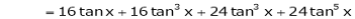
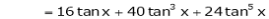
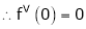
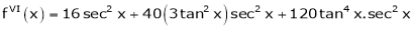
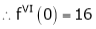
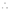 By equation (1)
By equation (1)
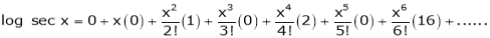
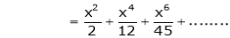
Prove that 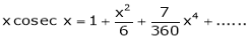
Solution:
Here f(x) = x cosec x
= 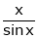
Now we know that
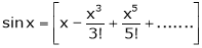
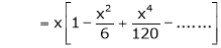
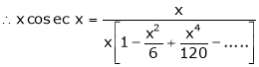
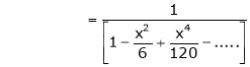

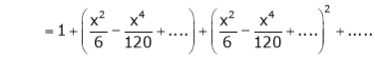
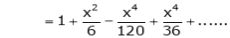
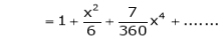
Q. Expand 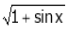 upto x6
upto x6
Solution:
Here 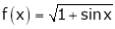
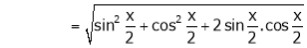
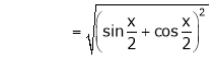

Now we know that
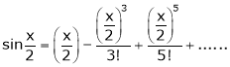 … (1)
… (1)
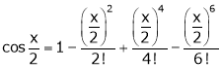 … (2)
… (2)
Adding (1) and (2) we get
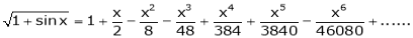
Q. Show that 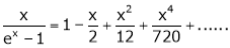
Solution:
Here 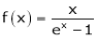
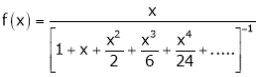

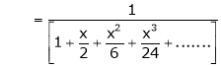
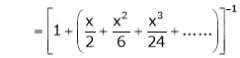

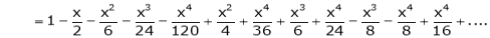

Thus

Taylor’s Series Expansion:
a) The expansion of f(x+h) in ascending power of x is
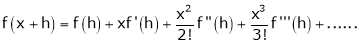
b) The expansion of f(x+h) in ascending power of h is
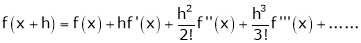
c) The expansion of f(x) in ascending powers of (x-a) is,
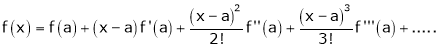
Using the above series expansion we get series expansion of f(x+h) or f(x).
Expansion of functions using standard expansions-
Example-1: Expand 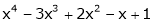 in power of (x – 3)
in power of (x – 3)
Solution:
Let 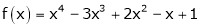
Here a = 3
Now by Taylor’s series expansion,
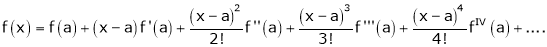 … (1)
… (1)
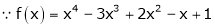
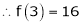

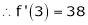

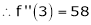
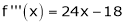
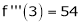
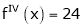

 equation (1) becomes.
equation (1) becomes.
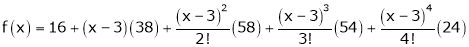

Example-2:
Using Taylors series method expand 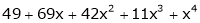 in powers of (x + 2)
in powers of (x + 2)
Solution:
Here 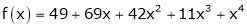
a = -2
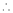 By Taylors series,
By Taylors series,
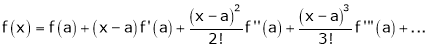 … (1)
… (1)
Since

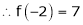
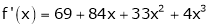
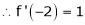
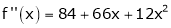
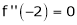
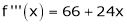
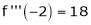
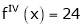
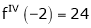 ,
, 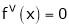 , …..
, …..
Thus equation (1) becomes
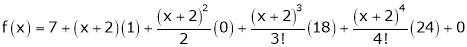
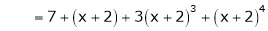
Example-3:
Expand 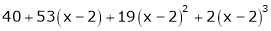 in ascending powers of x.
in ascending powers of x.
Solution:
Here
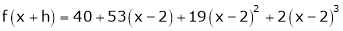
i.e. 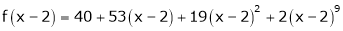
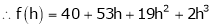
Here h = -2
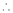 By Taylors series,
By Taylors series,
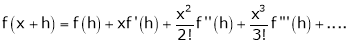 … (1)
… (1)
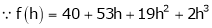
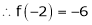
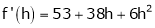



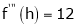
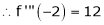
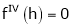
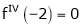
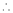 equation (1) becomes,
equation (1) becomes,

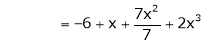
Thus
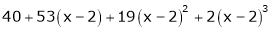
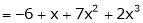
Example-4:
Expand 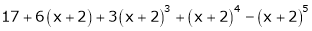 in powers of x using Taylor’s theorem,
in powers of x using Taylor’s theorem,
Solution:
Here
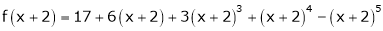
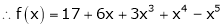
i.e. 
Here
h = 2
 By Taylors series
By Taylors series
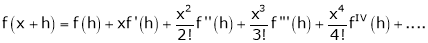 … (1)
… (1)
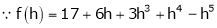
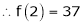

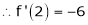
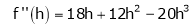
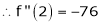
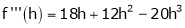

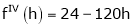

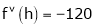
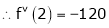
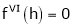
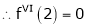
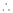 By equation (1)
By equation (1)
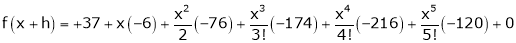
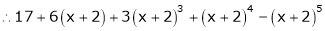
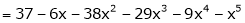
Key takeaways-
Taylor’s Series Expansion:-
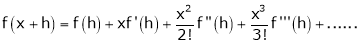
Taylor’s Series Expansion:-
a) The expansion of f(x+h) in ascending power of x is
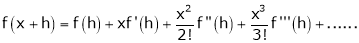
b) The expansion of f(x+h) in ascending power of h is
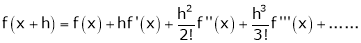
c) The expansion of f(x) in ascending powers of (x-a) is,
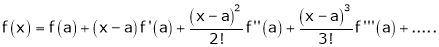
Using the above series expansion we get series expansion of f(x+h) or f(x).
Expansion of functions using standard expansions-
Example-1: Expand  in power of (x – 3)
in power of (x – 3)
Solution:
Let 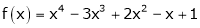
Here a = 3
Now by Taylor’s series expansion,
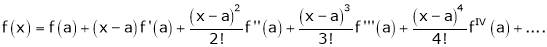 … (1)
… (1)
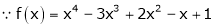
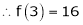
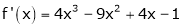
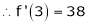
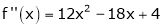
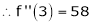
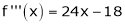

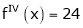
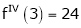
 equation (1) becomes.
equation (1) becomes.
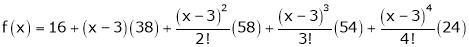
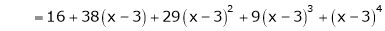
Example-2:
Using Taylors series method expand 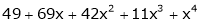 in powers of (x + 2)
in powers of (x + 2)
Solution:
Here 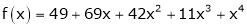
a = -2
 By Taylors series,
By Taylors series,
 … (1)
… (1)
Since

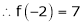
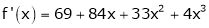

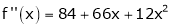

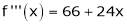

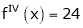
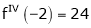 ,
, 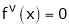 , …..
, …..
Thus equation (1) becomes
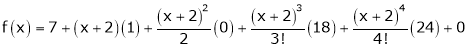
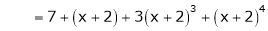
Example-3:
Expand 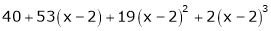 in ascending powers of x.
in ascending powers of x.
Solution:
Here
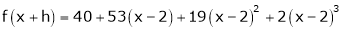
i.e. 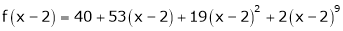
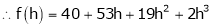
Here h = -2
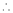 By Taylors series,
By Taylors series,
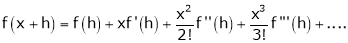 … (1)
… (1)
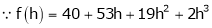
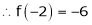
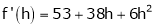


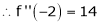
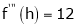
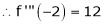

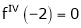
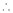 equation (1) becomes,
equation (1) becomes,
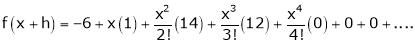

Thus
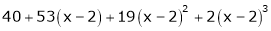
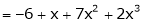
Example-4:
Expand 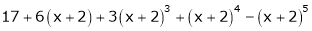 in powers of x using Taylor’s theorem,
in powers of x using Taylor’s theorem,
Solution:
Here
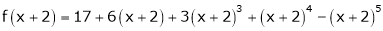
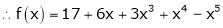
i.e. 
Here
h = 2
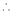 By Taylors series
By Taylors series
 … (1)
… (1)
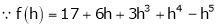
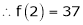
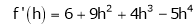
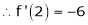
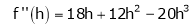
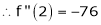
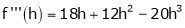
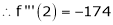
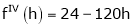
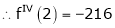
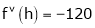
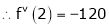
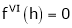

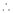 By equation (1)
By equation (1)
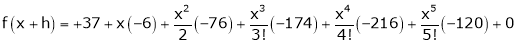
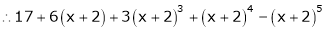
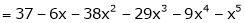
Key takeaways-
Taylor’s Series Expansion:-
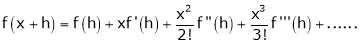
Exercise
a) Expand 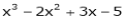 in powers of (x – 2)
in powers of (x – 2)
b) Expand 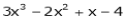 in powers of (x + 2)
in powers of (x + 2)
c) Expand 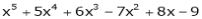 in powers of (x – 1)
in powers of (x – 1)
d) Using Taylors series, express 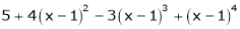 in ascending powers of x.
in ascending powers of x.
e) Expand 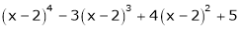 in powers of x, using Taylor’s theorem.
in powers of x, using Taylor’s theorem.
Function of two variables-
R denotes the set of real numbers. Let’s D is a collection of pairs of real numbers (x , y), which means D is a subset of R × R.
Then a real valued function of two variables of f is a rule that assign to each point (x,y) in D a unique real number denoted by f(x,y).
The set D is called the domain of f.
The set [ f(x,y) : (x,y) belongs to D ], which is the set of values the function f takes, is called range of f.
Here we genrally use the letter z to denote the value that a function of two variables takes,
Then we will have,
z = f(x, y)
Here we will call that z is the dependent variable and x and y are independent variables.
Example-1: The area of a rectangular figure whose length is l and breadth is b, given by l × b.
Here independent variables are l and b, but dependent variable is area.
Example-2: the volume of a cylinder is given by πr²h, where r is the radius and h is the height of the cylinder.
In which radius and height are independent variables and volume is dependent.
Example-3: the volume of cuboid is given by l × b× h. Where l, b and h are the length, breadth and height respectively.
L , b and h are independent variable and volume of cuboid is dependent variable.
Limits-
The function f(x,y) is said to tend to limit ‘l’ , as x →a and y→b Iff the limit is dependent on point (x,y) as x →a and y→b
We can write this as,
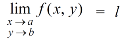
Example-1: Evaluate the 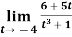
Sol. We can simply find the solution as follows,
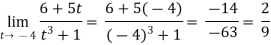
Example-2: Evaluate 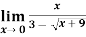
Sol.
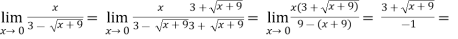 -6.
-6.
Example-3: evaluate 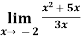
Sol.
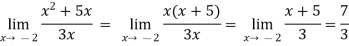
Conitinuity –
At point (a,b) , a function f(x,y) is said to be continuous if,
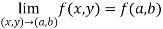
Working rule for continuity-
Step-1: f(a,b) should be well defined.
Step-2:  should exist.
should exist.
Step-3: 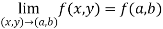
Example-1: Test the continuity of the following function-
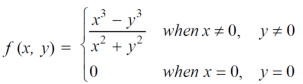
Sol. (1) the function is well defined at (0,0)
(2) check for the second step,
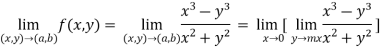

That means the limit exists at (0,0)
Now check step-3:
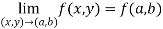
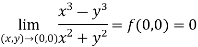
So that the function is continuous at origin.
Example-2: check for the continuity of the following function at origin,
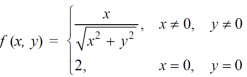
Sol. (1) Here the function is well defined at (0,0)
(2) check for second step-
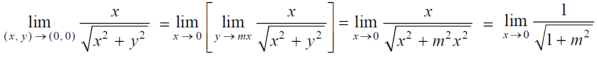
Limit f is not unique for different values of m
So that the limit does not exists.
Therefore the function is not continuous at origin.
Steps to check for existence of limit-
Step-1: find the value of f(x,y) along x →a and y→b
Step-2: find the value of f(x,y) along x →b and y→a
Note- if the values in step -1 and step-2 are same then we can say that the limits exist otherwise not.
Step-3: if a →0 and b→0 then find the limit along y =mx , if the value does not contain m then limit exist, If it contains m then the limit does not exist.
Note-1- put x = 0 and y = 0 in f , then find f1
2 - Put y = 0 and x = 0 In f then find x2
If f1 and f2 are equal then limit exist otherwise not.
3- put y = mx then find f3
If f1 = f2 ≠f3, limit does not exist.
4- put y = mx² and find f4,
If f1 = f2 = f3 ≠ f4 , limit does not exist
If f1 = f2 = f3 = f4 , limit exist.
Example-1: Evaluate 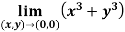
Sol . 1. 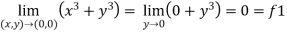
2. 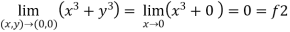
Here f1 = f2
3. Now put y = mx, we get
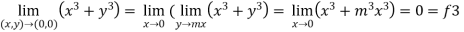
Here f1 = f2 = f3
Now put y = mx²
4. 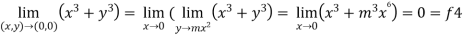
Therefore ,
F1 = f2 = f3 =f4
We can say that the limit exists with 0.
Example-2: evaluate the following-
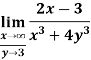
Sol. First we will calculate f1 –
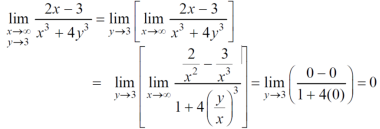
Here we see that f1 = 0
Now find f2,

Here , f1 = f2
Therefore the limit exists with value 0.
Partial derivatives
First order partial differentiation-
Let f(x , y) be a function of two variables. Then the partial derivative of this function with respect to x can be written as  and defined as follows:
and defined as follows:

Now the partial derivative of f with respect to f can be written as  and defined as follows:
and defined as follows:
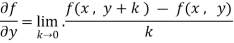
Note:
A. While calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating , as constant.
B. We apply all differentiation rules.
Higher order partial differentiation-
Let f(x , y) be a function of two variables. Then its second-order partial derivatives, third order partial derivatives and so on are referred as higher order partial derivatives.
These are second order four partial derivatives:
(a) 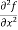 =
= 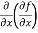
(b) 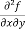 =
= 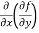
(c) 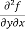 =
= 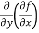
(d) 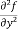 =
= 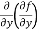
b and c are known as mixed partial derivatives.
Similarly we can find the other higher order derivatives.
Example-1: Calculate 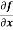 and
and 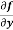 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Sol. To calculate  treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
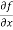 =
= 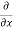 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 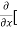 3x³] -
3x³] - 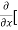 5y²] +
5y²] + 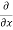 [2xy] -
[2xy] -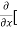 8x] +
8x] +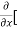 4y] -
4y] -  20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
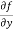 =
=  [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 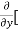 3x³] -
3x³] - 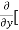 5y²] +
5y²] + 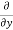 [2xy] -
[2xy] - 8x] +
8x] +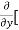 4y] -
4y] - 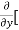 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Example-2: Calculate 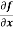 and
and 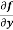 for the following function
for the following function
f( x, y) = sin(y²x + 5x – 8)
Sol. To calculate 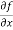 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
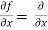 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)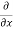 (y²x + 5x – 8)
(y²x + 5x – 8)
= (y² + 50)cos(y²x + 5x – 8)
Similarly partial derivative of f(x,y) with respect to y is,
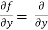 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)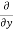 (y²x + 5x – 8)
(y²x + 5x – 8)
= 2xy cos(y²x + 5x – 8)
Example-3: Obtain all the second order partial derivative of the function:
f( x, y) = ( x³y² - xy⁵)
Sol.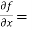 3x²y² - y⁵,
3x²y² - y⁵, 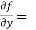 2x³y – 5xy⁴,
2x³y – 5xy⁴,
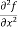 =
= 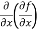 = 6xy²
= 6xy²
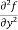 =
= 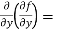 2x³ - 20xy³
2x³ - 20xy³
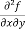 =
= 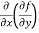 = 6x²y – 5y⁴
= 6x²y – 5y⁴
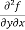 =
=  = 6x²y - 5y⁴
= 6x²y - 5y⁴
Example-4: Find

Sol. First we will differentiate partially with respect to r,
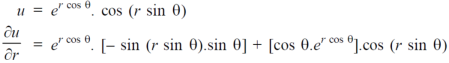
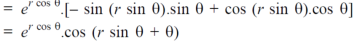
Now differentiate partially with respect to θ, we get
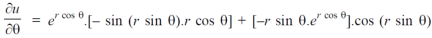

Example-5: if,
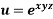
Then find.

Sol-
We have

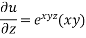
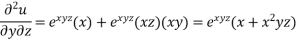
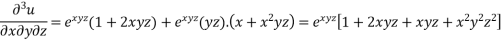
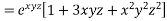
Example-6: if 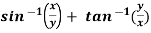 , then show that-
, then show that- 
Sol. Here we have,
u = 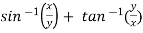 …………………..(1)
…………………..(1)
Now partially differentiate eq.(1) w.r to x and y , we get
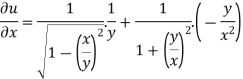
= 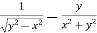
Or
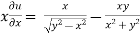 ………………..(2)
………………..(2)
And now,
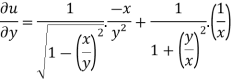
= 
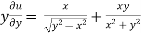 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
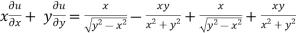 = 0
= 0
Hence proved.
Derivatives of composite and implicit functions
A composite function is a composition / combination of the functions. In this value of one function depends on the value of another function. A composite function is created when one function is put in another.
Let 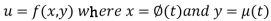
i.e 
To differentiate composite function chain rule is used:
Chain rule:
- If
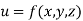 where x,y,z are all the function of t then
where x,y,z are all the function of t then
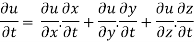
2. If 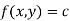 be an implicit relation between x and y .
be an implicit relation between x and y .
Differentiating with respect to x we get
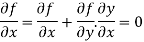
We get 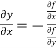
Example1: If 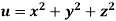 where
where 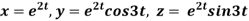 then find the value of
then find the value of 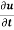 ?
?
Sol.
Given 
Where 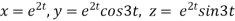
By chain rule
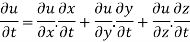

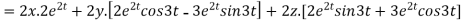
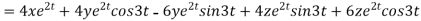
Now substituting the value of x ,y,z we get
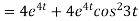 -6
-6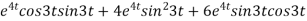
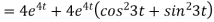
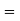 8
8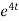
Example2: If 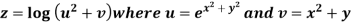 then calculate
then calculate 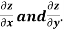
Sol
Given 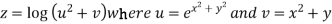
By Chain Rule
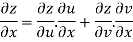
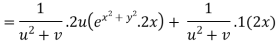
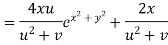
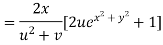
Putting the value of u = 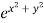
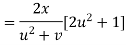
Again partially differentiating z with respect to y
By Chain Rule
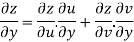
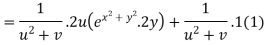
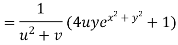
 by substituting value
by substituting value 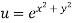
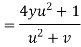
Example 3 :If 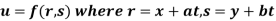 .
.
Show that 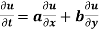
Given 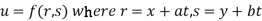
Partially differentiating u with respect to x and using chain rule
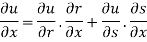

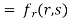 ………(i)
………(i)
Partially differentiating z with respect to y and using chain rule

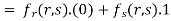
= 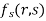 ………..(ii)
………..(ii)
Partially differentiating z with respect to t and using chain rule
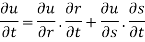
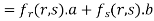
Using (i) and (ii) we get
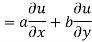
Hence 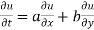

Example4: If 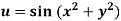 where the relation is
where the relation is 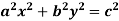 .
.
Find the value of 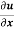
Let the given relation is denoted by 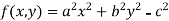
We know that 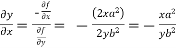
Differentiating u with respect to x and using chain rule

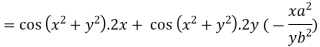
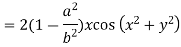
Example5 : If  and the relation is
and the relation is 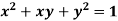 . Find
. Find 
Given relation can be rewrite as
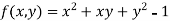 .
.
We know that

Differentiating u with respect to x and using chain rule
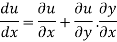
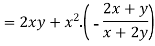
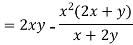
Implicit differentiation-
Let f(x,y) = 0
Where y = ∅(x)
By the chain rule , with x = x and y = ∅(x), we get
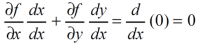
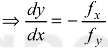
Here we assume that y is a differentiable funtion of x.
Example-1: if ∅ is a differentiable function such that y = ∅(x) satisfies the equation
x³ + y³ +sin xy = 0 then find 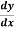 .
.
Sol. Suppose f(x,y) = x³ + y³ +sin xy
Then,
fᵡ = 3x² + y cos xy
Fy = 2y + x cos xy
So,

Example-2:
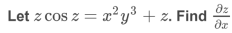
Sol. Take partial derivative on both side w.r. t. x , treat y as constant
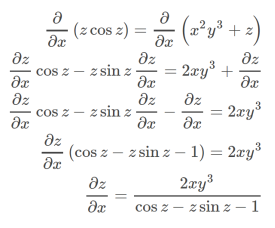
Example-3: if x²y³ + cos y cos z = x² cos x sin y, then find 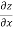
Sol. Differentiate partially w.r.t. x and treat y as constant,
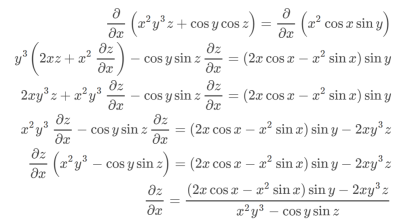
Key takeaways-
- The function f(x,y) is said to tend to limit ‘l’ , as x →a and y→b Iff the limit is dependent on point (x,y) as x →a and y→b
- Let f(x , y) be a function of two variables. Then the partial derivative of this function with respect to x can be written as
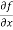 and defined as follows:
and defined as follows:
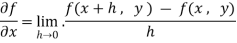
3. While calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating , as constant.
(a)  =
= 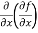
(b) 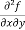 =
= 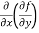
(c) 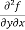 =
= 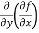
(d) 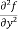 =
= 
Homogeneous function - A function f(x,y) is said to be homogeneous of degree n if,
f(kx, ky) = kⁿf(x, y)
Here, the power of k is called the degree of homogeneity.
Or
A function f(x,y) is said to be a homogenous function in which the power of each term is the same.
Example:
1. The function-

Is a homogeneous function of order 3.
Euler’s theorem
Statement – if u = f(x, y) be a homogeneous function in x and y of degree n , then
x + y
+ y 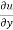 = nu
= nu
Proof: Here u is a homogeneous function of degree n,
u = xⁿ f(y/x) ----------------(1)
Partially differentiate equation (1) with respect to x,
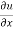 = n
= n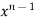 f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).(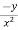 )
)
Now multiplying by x on both sides, we get
x = n
= n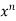 f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).(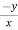 ) ---------- (2)
) ---------- (2)
Again partially differentiate equation (1) with respect to y,
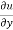 = xⁿ f’(y/x).
= xⁿ f’(y/x).
Now multiplying by y on both sides,
y 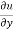 = xⁿ f’(y/x).
= xⁿ f’(y/x). ---------------(3)
---------------(3)
By adding equation (2) and (3),
x y
y 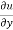 = n
= n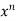 f(y/x) + + xⁿ f’(y/x).(
f(y/x) + + xⁿ f’(y/x).(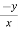 ) + xⁿ f’(y/x).
) + xⁿ f’(y/x).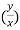
x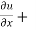 y
y 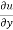 = n
= n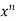 f(y/x)
f(y/x)
Here u = f( x, y) is homogeneous function, then - u =  f(y/x)
f(y/x)
Put the value of u in equation (4),
x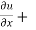 y
y 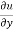 = nu
= nu
Which is the Euler’s theorem.
Let’s understand Eulers’s theorem by some examples:
Example1- If u = x²(y-x) + y²(x-y), then show that 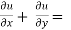 -2 (x – y)²
-2 (x – y)²
Solution - here, u = x²(y-x) + y²(x-y)
u = x²y - x³ + xy² - y³,
Now differentiate u partially with respect to x and y respectively,
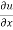 = 2xy – 3x² + y² --------- (1)
= 2xy – 3x² + y² --------- (1)
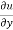 = x² + 2xy – 3y² ---------- (2)
= x² + 2xy – 3y² ---------- (2)
Now adding equation (1) and (2), we get
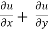 = -2x² - 2y² + 4xy
= -2x² - 2y² + 4xy
= -2 (x² + y² - 2xy)
= -2 (x – y)²
Example2- If u = xy + sin(xy), show that  =
= 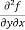 .
.
Solution – u = xy + sin(xy)
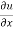 = y+ ycos(xy)
= y+ ycos(xy)
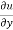 = x+ xcos(xy)
= x+ xcos(xy)
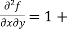 x (- sin(xy).(y)) + cos(xy)
x (- sin(xy).(y)) + cos(xy)
= 1 – xysin(xy) + cos(xy) -------------- (1)
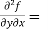 1 + cos(xy) + y(-sin(xy) x)
1 + cos(xy) + y(-sin(xy) x)
= 1 – xysin(xy) + cos(xy) -----------------(2)
From equation (1) and (2),
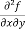 =
= 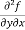
Example-3: If u(x,y,z) = log( tan x + tan y + tan z) , then prove that ,

Sol. Here we have,
u(x,y,z) = log( tan x + tan y + tan z) ………………..(1)
Diff. Eq.(1) w.r.t. x , partially , we get
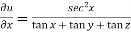 ……………..(2)
……………..(2)
Diff. Eq.(1) w.r.t. y , partially , we get
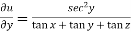 ………………(3)
………………(3)
Diff. Eq.(1) w.r.t. z , partially , we get
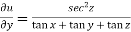 ……………………(4)
……………………(4)
Now multiply eq. 2 , 3 , 4 by sin 2x , sin 2y , sin 2z respectively and adding , in order to get the final result,
We get,
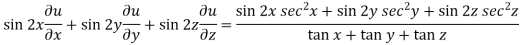
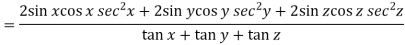
= 
So that,
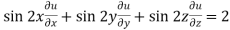 hence proved.
hence proved.
Key takeaways-
- A function f(x,y) is said to be a homogenous function in which the power of each term is the same.
- Euler’s theorem- if u = f(x, y) be a homogeneous function in x and y of degree n , then
x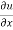 + y
+ y 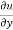 = nu
= nu
If f(x + h) is a function of h which can be expanded in the ascending powers of h and is differentiable by any number of times with respect to h, then-
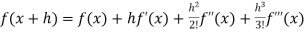 + …….+
+ …….+ 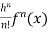 + ……..
+ ……..
Which is called Taylor’s theorem.
If we put x = a, we get-
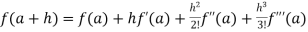 + …….+
+ …….+ 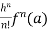 + …….. (1)
+ …….. (1)
Example-1: Express the polynomial 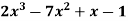 in powers of (x-2).
in powers of (x-2).
Sol. Here we have,
f(x) = 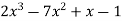
Differentiating the function w.r.t. x-
f’(x) = 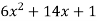
f’’(x) = 12x + 14
f’’’(x) = 12
f’’’’(x)=0
Now using Taylor’s theorem-
 + ……. (1)
+ ……. (1)
Here we have, a = 2,
Put x = 2 in the derivatives of f(x), we get-
f(2) = 
f’(2) = 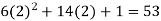
f’’(2) = 12(2)+14 = 38
f’’’(2) = 12 and f’’’’(2) = 0
Now put a = 2 and substitute the above values in equation(1), we get-
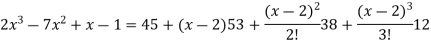
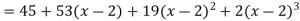
Taylor’s theorem for functions of two variables-
Suppose f(x , y) be a function of two independent variables x and y. Then,
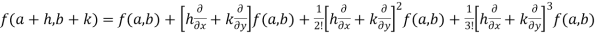 + ……………
+ ……………
Maclaurin’s series is the special case of Taylor’s series-
When we put a = 0 and b = 0 (about origin) in Taylor’s series, we get-
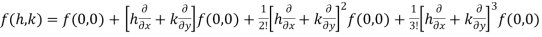 + ……………
+ ……………
Example-2: Expand f(x , y) = 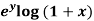 in powers of x and y about origin.
in powers of x and y about origin.
Sol. Here we have the function-
f(x , y) = 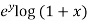
Here , a = 0 and b = 0 then
f(0 , 0) = 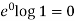
Now we will find partial derivatives of the function-
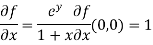
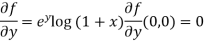
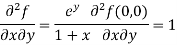
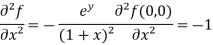

Now using Taylor’s theorem-
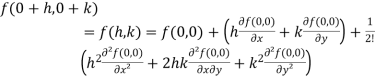 +………
+………
Suppose h = x and k = y, we get
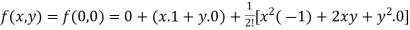 +…….
+…….
=  +……….
+……….
Example-3: Find the Taylor’s expansion of 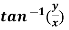 about (1 , 1) up to second degree term.
about (1 , 1) up to second degree term.
Sol. We have,

At (1, 1)

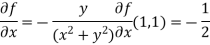
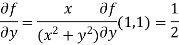
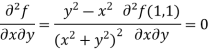
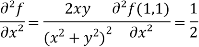
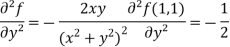
Now by using Taylor’s theorem-
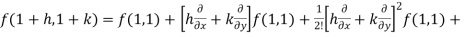 ……
……
Suppose 1 + h = x then h = x – 1
1 + k = y then k = y - 1
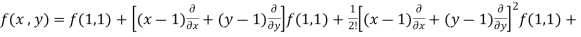 ……
……
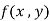 =
= 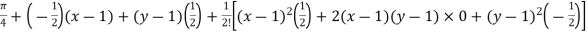
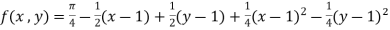 ……..
……..
Key takeaways-
- Taylor’s Theorem-
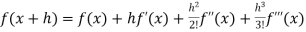 + …….+
+ …….+  + ……..
+ ……..
2. Maclaurin’s Theorem-
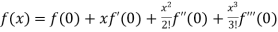 + …….
+ …….
Maxima and minima of function of two variables-
As we know that the value of a function at maximum point is called maximum value of a function. Similarly the value of a function at minimum point is called minimum value of a function.
The maxima and minima of a function is an extreme biggest and extreme smallest point of a function in a given range (interval) or entire region. Pierre de Fermat was the first mathematician to discover general method for calculating maxima and minima of a function. The maxima and minima are complement of each other.
Maxima and Minima of a function of one variables
If f(x) is a single valued function defined in a region R then
Maxima is a maximum point 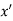 if and only if
if and only if 
Minima is a minimum point 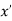 if and only if
if and only if 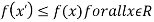




Maxima and Minima of a function of two independent variables
Let 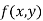 be a defined function of two independent variables.
be a defined function of two independent variables.
Then the point 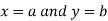 is said to be a maximum point of
is said to be a maximum point of  if
if
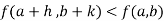
Or 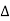 =
= 
For all positive and negative values of h and k.
Similarly the point  is said to be a minimum point of
is said to be a minimum point of  if
if
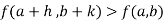
Or 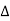 =
= 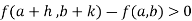
For all positive and negative values of h and k.
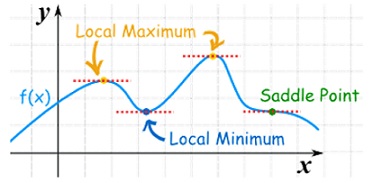
Saddle point:
Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point.
A point is a saddle point of a function of two variables if
![2 2 [ 2 ] 2
@f-= 0, @f--= 0, and @-f- @-f-- -@-f- < 0
@x @y @x2 @y2 @x @y](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642679241_1150193.png)
At the point.
Stationary Value
The value 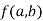 is said to be a stationary value of
is said to be a stationary value of 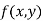 if
if
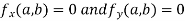
i.e. the function is a stationary at (a , b).
Rule to find the maximum and minimum values of 
- Calculate
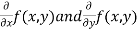 .
. - Form and solve
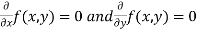 , we get the value of x and y let it be pairs of values
, we get the value of x and y let it be pairs of values 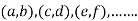
- Calculate the following values :
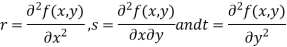
4. (a) If 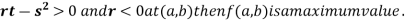
(b) If 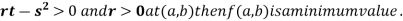
(c) If 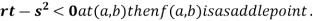
(d) If 
Example1 Find out the maxima and minima of the function
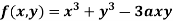
Given 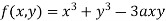 …(i)
…(i)
Partially differentiating (i) with respect to x we get
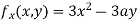 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
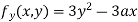 ….(iii)
….(iii)
Now, form the equations 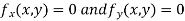
Using (ii) and (iii) we get
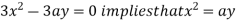
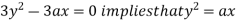
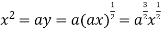 using above two equations
using above two equations
Squaring both side we get
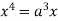
Or 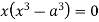
This show that 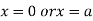
Also we get 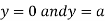
Thus we get the pair of value as 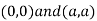
Now, we calculate

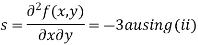
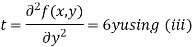
Putting above values in

At point (0,0) we get
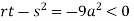
So, the point (0,0) is a saddle point.
At point 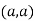 we get
we get
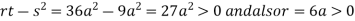
So the point  is the minimum point where
is the minimum point where 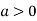
In case 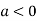
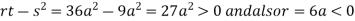
So the point 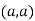 is the maximum point where
is the maximum point where 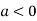
Example2 Find the maximum and minimum point of the function
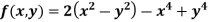
Partially differentiating given equation with respect to and x and y then equate them to zero
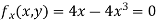
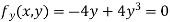
On solving above we get 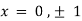
Also 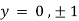
Thus we get the pair of values (0,0), (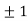 ,0) and (0,
,0) and (0,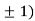
Now, we calculate
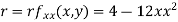
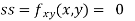
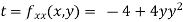
At the point (0,0)
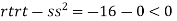
So function has saddle point at (0,0).
At the point (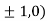
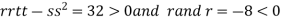
So the function has maxima at this point (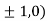 .
.
At the point (0,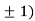
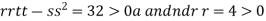
So the function has minima at this point (0,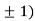 .
.
At the point (
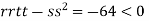
So the function has an saddle point at (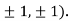
Key takeaways-
- The maxima and minima of a function is an extreme biggest and extreme smallest point of a function in a given range (interval) or entire region.
- If f(x) is a single valued function defined in a region R then
Maxima is a maximum point 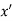 if and only if
if and only if 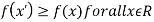
Minima is a minimum point 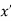 if and only if
if and only if 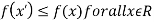
3. A point is a saddle point of a function of two variables if
![2 2 [ 2 ] 2
@f-= 0, @f--= 0, and @-f- @-f-- -@-f- < 0
@x @y @x2 @y2 @x @y](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642679245_399366.png)
At the point.
Let 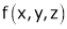 be a function of x, y, z which to be discussed for stationary value.
be a function of x, y, z which to be discussed for stationary value.
Let  be a relation in x, y, z
be a relation in x, y, z
 for stationary values we have,
for stationary values we have,
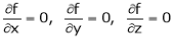
i.e.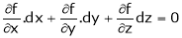 … (1)
… (1)
Also from 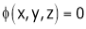 we have
we have
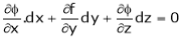 … (2)
… (2)
Let ‘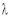 ’ be undetermined multiplier then multiplying equation (2) by
’ be undetermined multiplier then multiplying equation (2) by 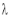 and adding in equation (1) we get,
and adding in equation (1) we get,
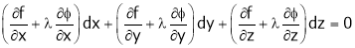
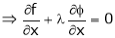 … (3)
… (3)
 … (4)
… (4)
 … (5)
… (5)
Solving equation (3), (4) (5) & we get values of x, y, z and 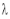 .
.
Q1) Decampere a positive number ‘a’ in to three parts, so their product is maximum
S1)
Let x, y, z be the three parts of ‘a’ then we get.
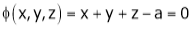 … (1)
… (1)
Here we have to maximize the product
i.e.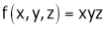
 By Lagrange’s undetermined multiplier, we get,
By Lagrange’s undetermined multiplier, we get,
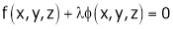
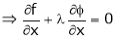 … (2)
… (2)
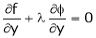 … (3)
… (3)
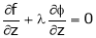 … (4)
… (4)
i.e.
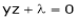 … (2)’
… (2)’
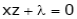 … (3)’
… (3)’
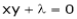 … (4)
… (4)

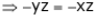
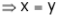
And 
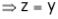
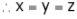
From (1)
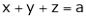


Thus 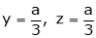 .
.
Hence their maximum product is 
Q2) Find the point on plane 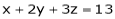 nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
S2)
Let 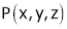 be the point on sphere
be the point on sphere 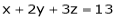 which is nearest to the point
which is nearest to the point 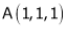 . Then shortest distance.
. Then shortest distance.
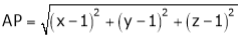
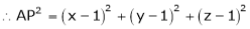
 Let
Let 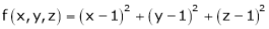
Under the condition 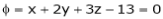 … (1)
… (1)
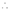 By method of Lagrange’s undetermined multipliers we have
By method of Lagrange’s undetermined multipliers we have
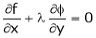
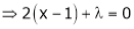 … (2)
… (2)
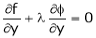
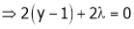 … (3)
… (3)
i.e.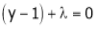 &
&
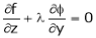
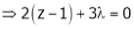 … (4)
… (4)
From (2) we get 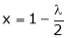
From (3) we get 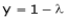
From (4) we get 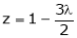
 Equation (1) becomes
Equation (1) becomes
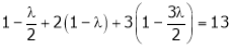
i.e.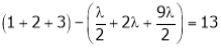
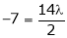
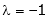
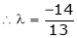
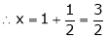
y = 2
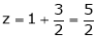
If 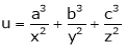 where x + y + z = 1.
where x + y + z = 1.
Prove that the stationary value of u is given by,
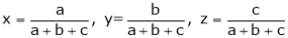
Example3 If 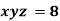 ,Find the value of x and y for which
,Find the value of x and y for which 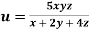 is maximum.
is maximum.
Given function is 
And relation is 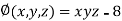
By Lagrange’s Method
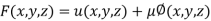
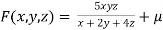 [
[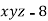 ] ..(i)
] ..(i)
Partially differentiating (i) with respect to x, y and z and equate them tozero
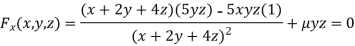
Or 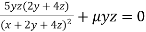 …(ii)
…(ii)
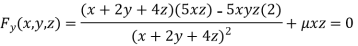
Or 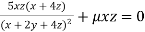 …(iii)
…(iii)
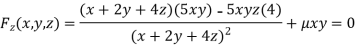
Or 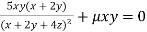 …(iv)
…(iv)
On solving (ii),(iii) and (iv) we get
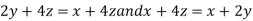
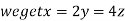
Using the given relation we get 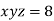
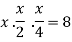
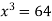
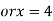
So that 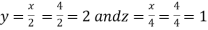
Thus the point for the maximum value of the given function is 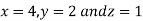
Example4 Find the points on the surface 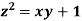 nearest to the origin.
nearest to the origin.
Let 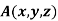 be any point on the surface, then its distance from the origin
be any point on the surface, then its distance from the origin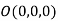 is
is
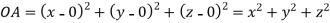
Thus the given equation will be
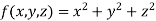
And relation is 
By Lagrange’s Method

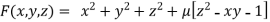 ….(i)
….(i)
Partially differentiating (i) with respect to x, y and z and equate them tozero

Or  …(ii)
…(ii)
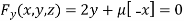
Or 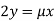 …(iii)
…(iii)
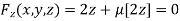
Or 
Or 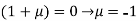
On solving equation (ii) by (iii) we get
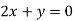
And 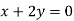
On subtracting we get 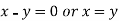
Putting in above 

Or 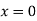
Thus 
Using the given relation we get
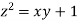 = 0.0 +1=1
= 0.0 +1=1
Or 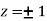
Thus point on the surface nearest to the origin is 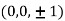
References:
1. G.B. Thomas and R.L. Finney, “Calculus and Analytic Geometry”, Pearson, 2002.
2. T. Veerarajan, “Engineering Mathematics”, McGraw-Hill, New Delhi, 2008.
3. B. V. Ramana, “Higher Engineering Mathematics”, McGraw Hill, New Delhi, 2010.
4. N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
5. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
6. HK Dass