Unit - 5
Partial Differential Equations
A differential equation involving partial derivatives with respect to more than one independent variable is called a partial differential equation.
The independent variables will be denoted by x and y and the dependent variable by z. The partial differential coefficients are denoted as-
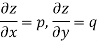
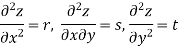
ORDER of a partial differential equation is the same as that of the order of the highest differential coefficient in it.
Classification of the partial differential equation-
Suppose the equation is-
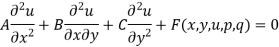
Here A, B, C are the constants of x and y, then the equation-
1. Elliptical- if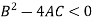 
2. Parabolic- if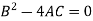 
3. Hyperbolic- if if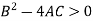 
Formation of the partial differential equation-
Method of elimination of arbitrary constants-
Example: Form a partial differential equation from-
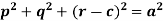
Sol.
Here we have-
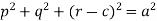
It contains two arbitrary constants a and c
Differentiate the equation with respect to p, we get-
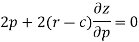
Or
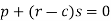
Now differentiate the equation with respect to q, we get-
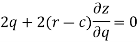
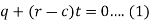
Now eliminate ‘c’,
We get
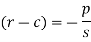
Now put z-c in (1), we get-
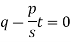
Or
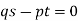
The second method we use is a method of elimination of arbitrary functions.
The solution of partial differential equation by direct partial Integration-
Example: Solve-
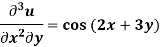
Sol.
Here we have-
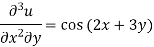
Integrate w.r.t. x, we get-
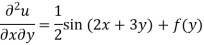
Integrate w.r.t. x, we get-
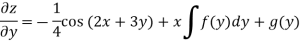
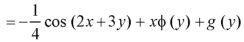
Integrate w.r.t. y, we get-
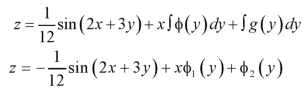
Example: Solve the differential equation-
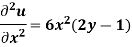
Given the boundary condition that-
At x = 0, 
Sol.
Here we have-
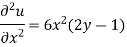
On integrating partially with respect to x, we get-
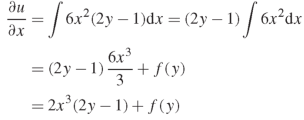
Here f(y) is an arbitrary constant.
Now form the boundary condition-
When x = 0,
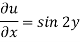
Hence-
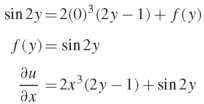
On integrating partially w.r.t.x, we get-
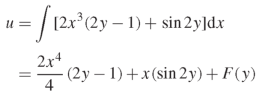
Example: Solve the differential equation-
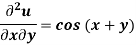
Given that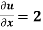 
when y = 0, and u = 
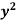when x = 0.
Sol.
We have-
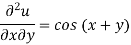
Integrating partially w.r.t. y, we get-
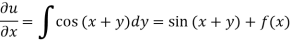
Now from the boundary conditions,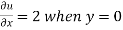 
Then-
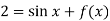
From which,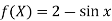
It means,
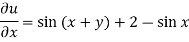
On integrating partially w.r.t. x givens-
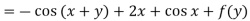
From the boundary conditions, u =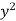 
when x = 0
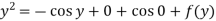
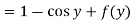
From which-
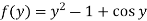
Therefore, the solution of the given equation is-
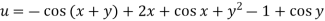
Key takeaways:
1. Order of a partial differential equation is the same as that of the order of the highest differential coefficient in it.
2. Elliptical- if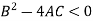 
3. Parabolic- if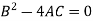 
4. Hyperbolic- if if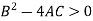 
Linear Equations of the First Order
A linear partial differential equation of the first order, commonly known as Lagrange’s Linear equation is of the form
Pp + Qq = R (1)
Where, P, Q, and R are functions of x, y, z. This equation is called a quast linear equation. When P, Q, and R are independent of z it is known as a linear equation.
Such an equation is obtained by eliminating an arbitrary function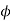 
from 
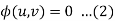
Where u,v are some functions of x, y, z.
Differentiating (2) partially with respect to x and y
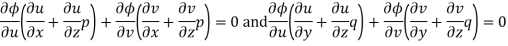
Eliminating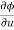 
and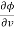 
, we get
Which simplifies to
This is of the same form as (1)
Now suppose u = a and v=b, where a, b are constants, so that
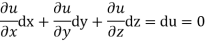
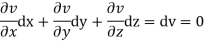
By cross multiplication we have,
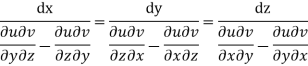
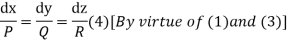
The solution of these equations are u = a and v = b
Therefore,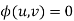 
is the required solution of (1).
Thus to solve the equation Pp + Qq =R.
(i) Form the subsidiary equations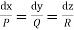 
(ii) Solve these simultaneous equations
(iii) Write the complete solution as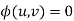 
or u=f(v)
Method of multipliers-
Let the auxiliary equation be
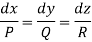
L, m, n may be the constants of x, y, z then we have-
L, m, n are selected in such a way that-
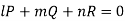
Thus
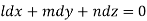
On solving this differential equation, if the solution is- u =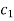 
Similarly, choose another set of multipliers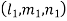 
and if the second solution is v =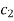 
So that the required solution is f(u, v) = 0.
Example. Solve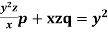 
(Kottayam, 2005)
Solution. Rewriting the given equation as
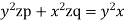
The subsidiary equations are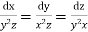 
The first two fractions give 
Integrating we get 
n(i)
Again the first and third fraction give xdx = zdz
Integrating, we get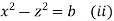 
Hence from (i) and (ii), the complete solution is
Example. Solve 
Solution. Here the subsidiary equations are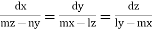 
Using multipliers x,y, and z we get each fraction =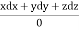 
which on integration gives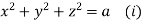 
Again using multipliers l, m and n we get each fraction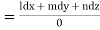 
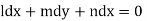which on integration gives lx +my +nz = b (ii)
Hence from (i) and (ii), the required solution is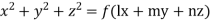 
Example. Solve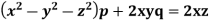 
Solution. Here the subsidiary equations are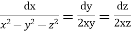 
From the last two fractions, we have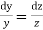 
Which on integration gives log y = log z + log a or y/z=a (i)
Using multipliers x, y and z we have
Each fraction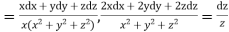 
Which on integration gives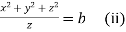
Hence from (i) and (ii), the required solution is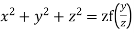 
Example: Solve-
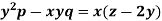
Sol.
We have-
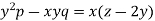
Then the auxiliary equations are-
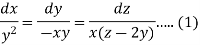
Consider the first two equations only-
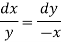
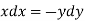
On integrating
…….. (2)
Now consider the last two equations-
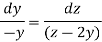
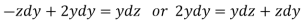
On integrating we get-
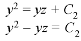…………… (3)
From equation (2) and (3)-
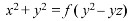
Example: Find the general solution of-
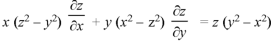
Sol. The auxiliary simultaneous equations are-
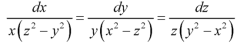……….. (1)
Using multipliers x, y, z we get-
Each term of (1) equals to-
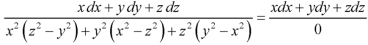
Xdx + ydy + zdz=0
On integrating-
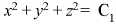………… (2)
Again equation (1) can be written as-
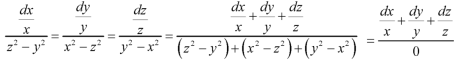
Or
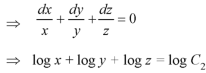
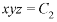………….. (3)
From (2) and (3), the general solution is-
Key takeaways:
A linear partial differential equation of the first order, commonly known as Lagrange’s Linear equation is of the form
Pp + Qq = R
Type-1: Equation of the type f(p, q) = 0
Method-
Let the required solution is-
Z = ax + by + c …….. (1)
So that-
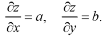
On putting these values in f(p, q) = 0
We get-
f(a, b) = 0
So from this, find the value of b in terms of a and put the value of b in (1). It will be the required solution.
Type-2: Equation of the type-
Z = px + qy + f(p, q)
Its solution will be-
Z = ax + by + f(a, b)
Type-3: Equation of the type f(z, p, q) = 0
Type-4: Equation of the type-
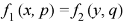
Method-
Let-
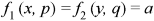
Example: Solve-
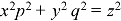
Sol.
This equation can be transformed as-
………. (1)
Let
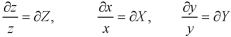
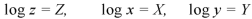
Equation (1) can be written as-
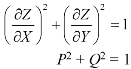………… (2)
Let the required solution be-
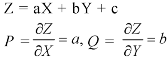
From (2) we have-
Example: Solve-
Sol.
Let u = x + by
So that-
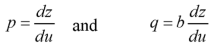
Put these values of p and q in the given equation, we get-
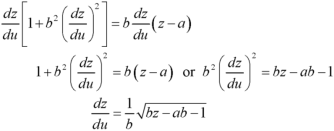
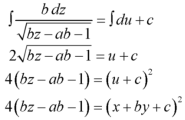
Example: Solve-
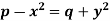
Sol.
Let-
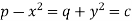
That means-
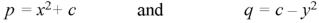
Put these values of p and q in
This is the general method for finding the complete integral of a non-linear partial differential equation.
Let us consider the equation-
f(x, y, z , p, q) = 0 ………. (1)
Since z depends on x and y, we have-
The main thing in Charpit’s method is to find another relationship between the variables x, y, z, and p. q.
And let the relation be-
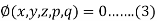
Here on solving equations (1) and (2), we get the values of p and q.
When we substitute these values of p and q in (2), it becomes integrable.
To determine 
, equations (1) and (3) are differentiated with respect to x and y.
We get, when we differentiate with respect to x,
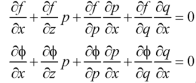
We get, when we differentiate with respect to y,
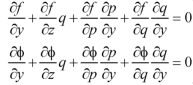
Eliminating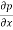 
between the equations we get from differentiating for x, we get
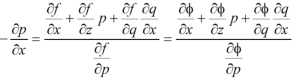
Or
…………(4)
Eliminating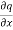 
between the equations we get from differentiating for y, we get
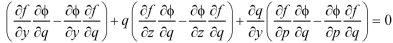…………(5)
Adding (4) and (5) and keeping in view the relation on, the terms of the last brackets of (4) and (5) cancel. On rearranging, we get-
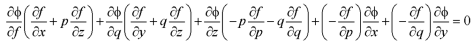
Or
This equation is Lagrange’s linear equation of the first order with x, y, z, p, q as independent variables and equation (4) as the dependent variable.
Its subsidiary equations are-
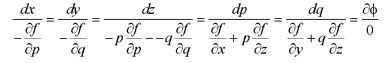
An integral of these equations involving p or q or both can be taken as the relation (3) which along with (1) will give the values of p and q to make (2) integrable.
Example: Solve-
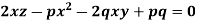
Sol.
Let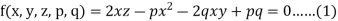
Charpit’s subsidiary equations are-
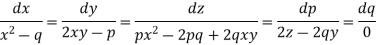
So that- dq = 0 or q = a
On putting q = a in (1) we get-
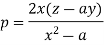
Such that-
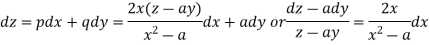
Integrating
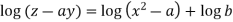
Or
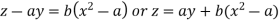
Which is the required solution.
Example: Solve-
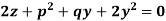
Sol.
Let
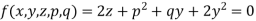
Charpit’s subsidiary equations are-
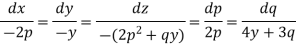
From the first and fourth ratios,
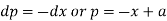
Substituting p = a – x in the given equation, we get-
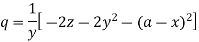
So that-
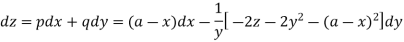
Multiply both sides by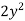 
,
Integrating-
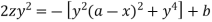
Or
Which is the required solution.
Classification of PDE:
The second order PDE in two independent variables of the form
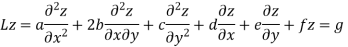
Here a,b,c,d,e,f and g are the functions of the independent variables x and y.
The principal part of the operator L, can be given as-
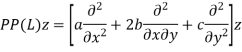
The equation is classified as-
Hyperbolic if-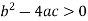 
Parabolic if-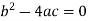 
Elliptic if-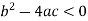 
Here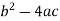 
is the discriminant of the operator L.
Example: Classify the following PDEs into hyperbolic, parabolic or elliptic.
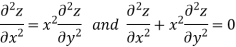
Sol. In the first PDE, a = 1, b = 0 and c =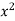 
So that-
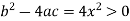
Thus we can say that the given PDE is hyperbolic.
Now in second PDE,
A = 1, b = 0 and c = 
So that-
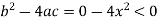
Therefore the second PDE is elliptic.
Solution of wave equations
D'Alembert's solution of the wave equation
The method of d'Alembert provides a solution to the one-dimensional wave equation
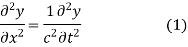
That models vibrations of a string.
The general solution can be obtained by introducing new variables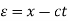 
and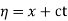 
, and applying the chain rule to obtain
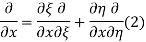
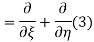
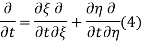
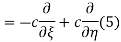
Using (4) and (5) to compute the left and right sides of (3) then gives
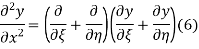
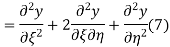
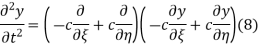
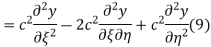
Respectively, so plugging in and expanding then gives
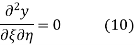
This partial differential equation has general solution
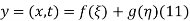
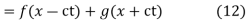
Where f and g are arbitrary functions, with f representing a right-traveling wave and g a left-traveling wave.
The initial value problem for a string located at position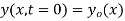 
as a function of distance along the string x and vertical speed 
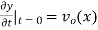can be found as follows. From the initial condition and (12),
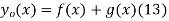
Taking the derivative with respect to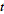 
then gives
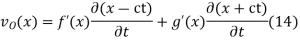
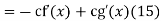
And integrating gives
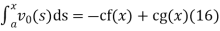
Solving (13) and (16) simultaneously for f and g immediately gives
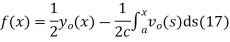
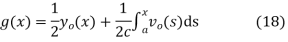
So plugging these into (13) then gives the solution to the wave equation with specified initial conditions as
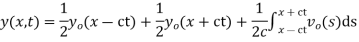
Example. Find the deflection of a vibrating string of unit length having fixed ends with initial velocity zero and initial deflection f (x)=k (sinx –sin2x)
Solution. By d’Alembert’s method, the solution is
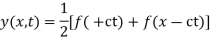
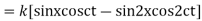
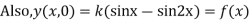
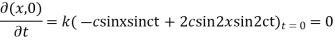
i.e., the given boundary corrections are satisfied.
Wave equation in two dimensions-
The equation
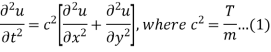
Is the wave equation in two dimensions.
Solution of wave equation in two dimensions (rectangular membrane)-
Let us assume that the solution of the above equation (1) is of the form-
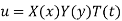
Put these values in the equation and dividing by XYT, we get-
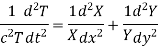
If each member is a constant then this can hold good.
Now choosing the constants suitably, we get-
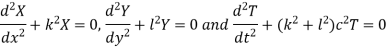
Hence the solution of equation (1) is-
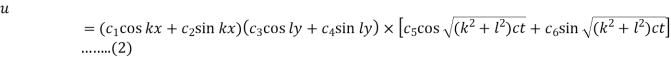
Now let the membrane is rectangular and it is stretched between the lines x = 0, x = a, y = 0, y = b.
Then the condition u = 0 when x = 0 gives-
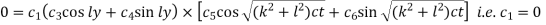
Then putting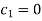 
in (2) and applying the condition u = 0, when x = a,we get-
Now applying the conditions u = , when y = 0 and y = b, we get
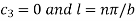
Therefore the solution (2) becomes-
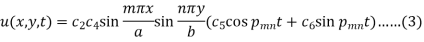
Where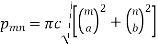 
Choosing the constant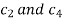 
so that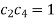 
We can write the general solution of the equation-1 as-
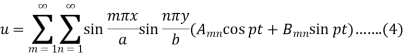
If the membrane starts from rest from the initial position u = f(x,y)
Which means-
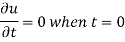
Then equation 3 gives-
Also using the condition u = f(x, y) when t = 0, we get-
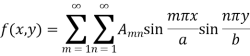
Which is the double Fourier series.
Now multiply the both sides by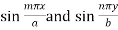 
and integrating from x = 0 to x = a and y = 0 to y = b,
Every term on the right except one, become 0, therefore we get-
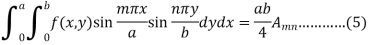
This is called the generalised Euler’s formula.
Example: Find the deflection u(x,y,t) of the square membrane with a = b = 1 and c = 1. If the initial velocity is zero and the initial deflection is f(x, y) =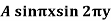 
.
Sol.
Here taking a = b = 1 and f(x, y) =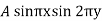 
in equation above (5)-
We get-
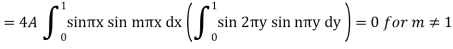
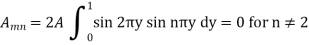
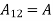
Also from equation (3) above-
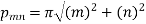
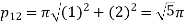
Therefore from equation (4),
The solution will be-
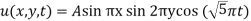
One and two dimensional heat flow equations
One dimensional heat flow
Suppose heat flow along a bar of uniform cross section in the direction perpendicular to the cross section. Take one end of the bar as origin and the direction of the heat flow is along x axis.
Let the temperature of the bar at any time t at a point x distance from the origin be u(x,t). Then the equation of one-dimensional heat flow is
Example. A rod of length 1 with insulated sides is initially at a uniform temperature u. Its ends are suddenly cooled to 0° Celsius and are kept at that temperature. Prove that the temperature function u (x, t) is given by
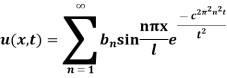
Where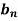 
is determined from the equation.
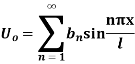
Solution. Let the equation for the conduction of heat be
Let us assume that u = XT, where X is a function of x alone and T that of t alone.
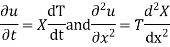
Substituting these values in (1) we get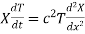 
i.e.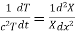 
Let each side be equal to a constant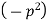 
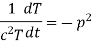
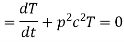
And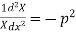 
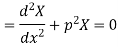
Solving (3) and (4) we have
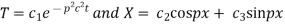
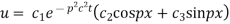
Putting x = 0, u = 0 in (5), we get
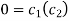
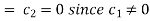
(5) becomes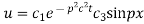 
Again putting x = l, u =0 in (6), we get
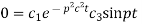
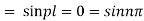
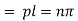
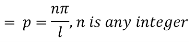
Hence (6) becomes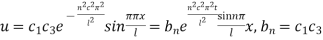 
This equation satisfies the given conditions for all integral values n. Hence taking n = 1, 2, 3,…, the most general solution is
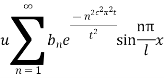
By initial conditions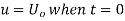 
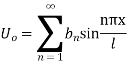
Example 2. Find the solution of
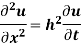
For which u ( 0, t) = u (l.t) =0 =sin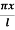 
bi method of variable separable.
Solution.
In example 10 the given equation was
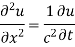
On comparing (1) and (2) we get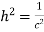 
Thus solution of (1) is
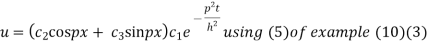
On putting x =0
u =0 in (3) we get
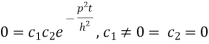
(3) reduced to
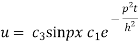
On putting x = l and u =0 in (4) we get
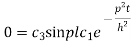
Now (4) is reduced to
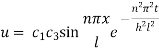
On putting t = 0, u =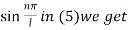 
This equation will be satisfied if
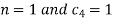
On putting the values of 
and n in (5) we have
Example 3. The ends A and B of a rod 20 cm long having the temperature at 30 degree Celsius and at 80 degree Celsius until steady state prevails. The temperature of the ends are changed to 40 degree Celsius and 60 degree Celsius respectively. Find the temperature distribution in the rod at time t.
Solution. The initial temperature distribution in the rod is
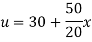
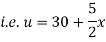
And the final distribution (i.e. steady state) is
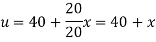
To get u in the intermediate period, reckoning time from the instant when the end temperature were changed we assumed
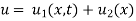
Where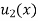 
is the steady state temperature distribution in the rod (i.e. temperature after a sufficiently long time) and 
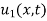is the transient temperature distribution which tends to zero as t increases.
Thus,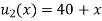 
Now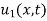 
satisfies the one dimensional heat flow equation
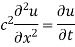
Hence u is of the form
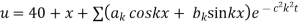
Since 
Hence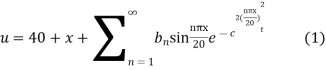 
Using the initial condition i.e.
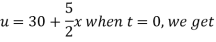
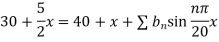
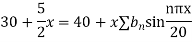
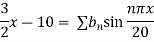
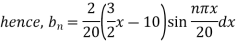
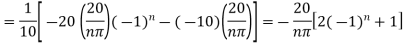
Putting this value of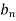 
n (1), we get
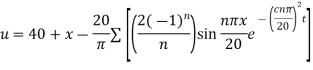
Two dimensional heat flow-
Let us consider the heat flow in a metal plate of uniform thickness, in the direction parallel to length and breadth of the plate.
Let u(x, y) be the temperature at any point (x, y) of the plate at time t is given as-
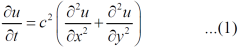
In the steady state, u doesn’t change with t,
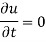
Equation (1) becomes-
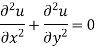
Which is known as Laplace’s equation in two dimensions.
Laplace equation in two dimensions
The equation-
Is known as the Laplace’s equation in two dimensions.
Solution of Laplace’s equation-
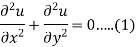
Let
Put the value in (1), we get-
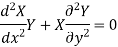
Separating the variables-
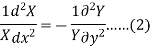
Since x and y are the independent variables, equation (2) can hold good only if each side of (2) is equal to a constant (k),
Then (2) leads the ordinary differential equation-
On solving these equations, we get-
- When k is positive and it is equals to
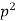, say
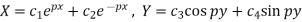
2. When k is negative and it is equals to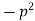 
, say
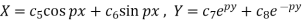
3. When k is zero-
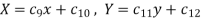
Example: Solve the Laplace’s equation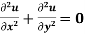 
subject to the conditions u(0, y) = u(l, y) = u(x, 0) = 0 and u(x, a) = sin n
Sol.
The three possible solutions of Laplace’s equation-
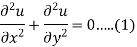
Are-
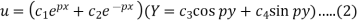
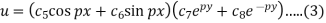
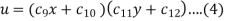
We need to solve equation (1) satisfying the following boundary conditions-
u(0, y) ........... (5)
u(l, y) = 0........(6)
u(x, 0) = 0 ..........(7)
And u(x, a) = sin n
...... (8)
Using (5), (6) and (2), we get-
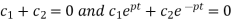
Solving these equations, we get-
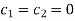
Which leads to trivial solution.
Similarly we get a trivial solution by using (5), (6) and (4).
Hence the solution for the present problem is solution (3).
Now using (5) in (3), we get-
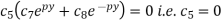
Therefore, equation (3) becomes-
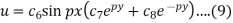
Using (6), we get-
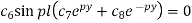
Therefore either-
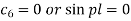
If we take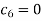 
then we get a trivial solution.
Thus sin pl = 0 whence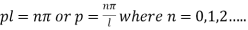 
Equation (9) becomes-
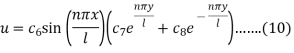
Using (6), we have 0 =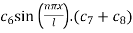 
i.e.
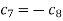
Thus the solution suitable for this problem is-
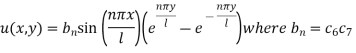
Now using the condition (8)-
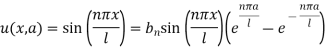
We get-
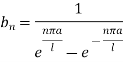
Hence the required solution is-
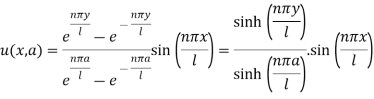
Key takeaways:
- Wave equation in two dimensions-
The equation
Is the wave equation in two dimensions.
2. The equation of one-dimensional heat flow is
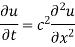
3. Laplace equation in two dimensions
The equation-
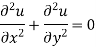
Is known as the Laplace’s equation in two dimensions.
Method of separation of variables
In this method, we assume that the dependent variable is the product of two functions, each of which involves only one of the independent variables. So to ordinary differential equations are formed.
Example: Using the method of separation of variables, solve
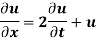
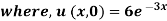
Solution.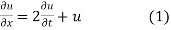 
Let, u = X(x). T (t). (2)
Where X is a function of x only and T is a function of t only.
Putting the value of u in (1), we get
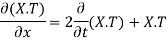
(a) 
On integration log X = cx + log a = log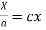 
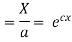
(b)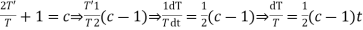 
On integration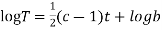 
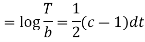
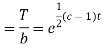
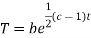
Putting the value of X and T in (2) we have
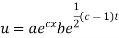
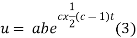
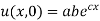
But,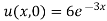 
i.e.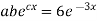 
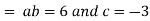
Putting the value of a b and c in (3) we have
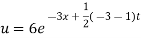
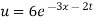
Which is the required solution.
Example. Use the method of separation of variables to solve equation
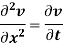
Given that v = 0 when t→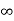
as well as v =0 at x = 0 and x = 1.
Solution.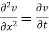 
Let us assume that v = XT where X is a function of x only and T that of t only
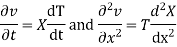
Substituting these values in (1), we get
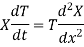
Let each side of (2) equal to a constant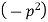 
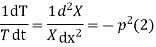
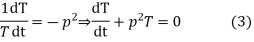
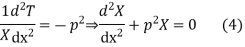
Solving (3) and (4) we have
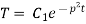
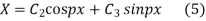
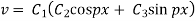
Putting x = 0, v = 0 in (5) we get
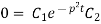
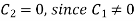
On putting the value of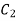 
in (5) we get
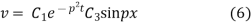
Again putting x = l, v= 0 in (6) we get
Since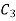 
cannot be zero.
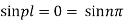
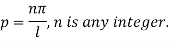
Inputting the value of p in (6) it becomes
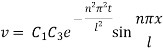
Hence,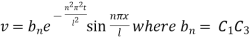 
This equation satisfies the given condition for all integral values of n. Hence taking n = 1, 2, 3,… the most general solution is
Example. Using the method of separation of variables, solv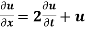e 
Where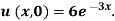 
Solution. Assume the given solution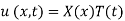 
Substituting in the given equation, we have
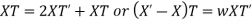
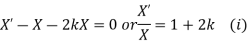
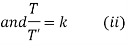
Solving (i)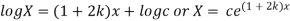 
From (ii)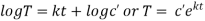 
Thus 
Now,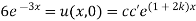 
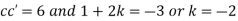
Substituting these values in (iii) we get
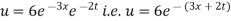
Which is the required solution.
Solution of heat equation by Fourier transform-
Example: Solve the equation-
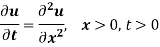
Subject to the conditions-
- u = 0 when x = 0, t>0
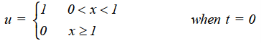
- U(x,t) is bounded.
Sol.
Here we apply Fourier sine transform-
We get-
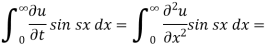
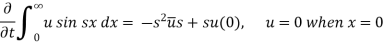
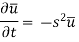
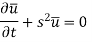
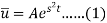
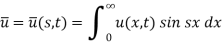
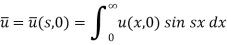
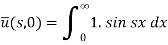
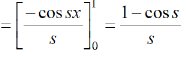...... (2)
Put the value of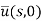 
in equation (1), we get
So that-
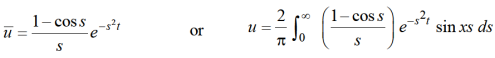
References:
1. R. J. Beerends H. G. Ter Morsche, J. C. Van Den Berg. L. M. Van De Vrie, Fourier and Laplace Transforms, Cambridge University Press.
2. Sastry S.S. Introductory Methods of Numerical Analysis, PHI.
3. B.S. Grewal: Higher Engineering Mathematics; Khanna Publishers, New Delhi.
4. B.V. Ramana: Higher Engineering Mathematics; Tata McGraw- Hill Publishing Company Limited, New Delhi.
5. Peter V.O’ Neil. Advanced Engineering Mathematics, Thomas (Cengage) Learning.
