Unit - 1
Introduction to Principles of Control System
1) Linear and Non-Linear system:
A system is said to be linear when it obeys law of superposition.
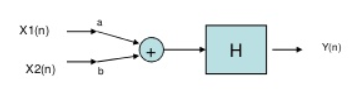
If we have two inputs x1(n) and x2(n), and output y(n). The operator ‘H’ is called linear operator if it satisfies the following condition.

Fig. Input first pass through adder
In the above figure first the two inputs pass through an adder than through the operator. So, the equation after adder will be ax1(n)+bx2(n). Now final output equation after passing through operator is
Y(n)=H[ax1(n)+bx2(n)]=Hax1(n)+H bx2(n)
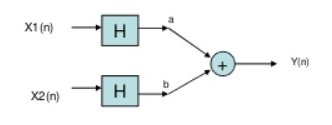
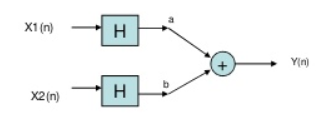
Fig. Input first pass through operator
Now, in above figure the two inputs first pass through the operator and then through the summer. The equation at output is
Y(n)= Hax1(n)+H bx2(n)
The two output equations in both the systems are same. Hence, the system operator H is linear.
Non-Linear system: If the system does not obey law of superposition, it is said to be non-linear.
2) Time variant and Time Invariant system: A time delay or advance in the input signal produces the corresponding change in the output. Then the system is said to be time invariant.
3) 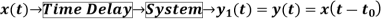
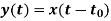
4) 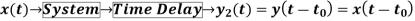
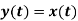
Fig: Time-Invariant system
If the delay or advance in the system does not produce corresponding change in the output then it’s called as Time variant System.
5) Causal and Anti-Causal system: A system is said to be causal if it’s output at any point of time depends only on the input x(t) for time ‘t’, where t<t0, where t0 is the present time. If not so then it is called as anti-causal system.
Only causal signals are realisable signals.
6) Memory and Memoryless System: A system is said to be memoryless if at any point of time the output depends only on present input but not on its past inputs.
If the system output at instance of time depends on the past inputs then it is called as memory system.
7) Invertible and Non-Invertible system: The system is said to be invertible if the input of the system can be recovered from the system output.
Key takeaway
Only causal signals are realisable signals
Que) For the system with y(t)=x(-t), find whether the system is linear or not?
Sol: To comment on linearity of system it should follow law of superposition. So, From model given below
Y(t)=ax1(-t)+bx2(-t)
Now from second model
Y(t)= ax1(-t)+bx2(-t)
Since, output from both the model is same so system is linear.
Que) For y(t)=cos[x(t)], comment whether it is time invariant or not?
Sol: From model 1
1) 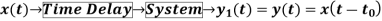
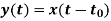
Y(t)=cos[x(t-t0)]
From model 2
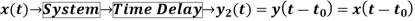
Y(t)=cos[x(t-t0)]
Since, time delay or advance in the input signal produces the corresponding change in the output. Hence, it is time invariant.
Que) For y(t)=x(t2), is the system causal or anti causal?
Sol: y(t)= x(t2)
If the output for any time depends on the future than its not causal. So, Let t=1
Y(1)=x(1)
t=2
y(2)=x(4)
Since, it depends on future values, so it is anti-causal.
Que) For y(t)=x(t)+2. Comment whether system has memory or memoryless?
Sol: For t=1
Y(1)=x(1)+2
For t=2
Y(2)=x(2)+2
So, for any value of t the output depends only on present input. Hence, it is memoryless.
Open loop systems:
This is the loop of control system without any feedback. In this the control action is not dependent on the desired output.

Fig. Open loop control system
Example of open Loop systems are the traffic signals, Automatic washing machine and in fields control d.c. Motor.
G(s) = c(s)/R(s) -------(1)
Closed loop systems:
This is a type of control system with feedback. In this type of system. The control action is dependent on the desired output.
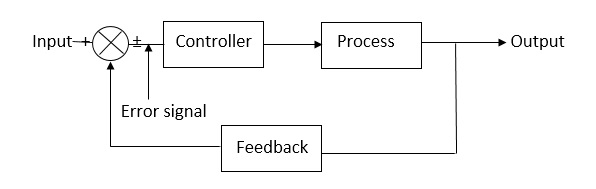
Fig. Closed Loop control system
The error signal is again fed to controller to the error and get desired output.
G(s) – forward amplification
H(s) _ Reverse amplification
Above system is with negative feedback.
Positive feedback is used only in oscillators and other use is not known as discussing only negative feedback.
[ R(s) – c(s) H (S) ] G(s) = c(s)
R (s) G(s) = [1+G(s) H(s)] c(s)
C(s)/R(S) = G(S)/1+G(s) H(s)
S0, the transfer function of closed Loop system is
C(s)/ R(S) = G(s)/ 1+G(S) H(S) --------(2)
If numerator of above equation (2) is equalized to zero we get zeros of closed Loop Transfer function [G(S) = 0]
If dominator of equation (2) is equaled to zero we get polls of the closed loop transfer function [ 1+G(s) H(S) = 0]
1+ G(S) H(s) = 0 [ characteristic Equation]
Stability of the system is determined by the location of its poles.
Comparisons between open Loop and Closed Loop system
Open Loop System | Closed Loop system |
1.It does Not have any feedback. | 1. This system comprise of feedback |
2.As no feedback so easier to build. | 2.As it has feedback so difficult to build |
3.Theaccuracy of this system depends on the calibration of input. | 3.They are accuracy because of the feedback. |
4.Open Loop system are more stable. | 4.In closed Loop system stability depends on system components. |
5.optimization is not possible | 5. Optimization is possible |
6.These systems are not reliable. | They are more reliable |
There are two types of feedbacks
i) Positive Feedback
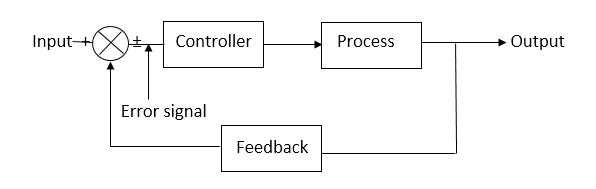
Fig. Closed Loop control system
In positive feedback systems the feedback signal is added to the input signal. The positive feedback is used only in oscillators. The transfer function is given as
C(s)/ R(S) = G(s)/ 1-G(S) H(S)
Ii) Negative Feedback
In negative feedback the error signal is inverted at the input signal. The discussion in this unit is based on this negative feedback systems only. The transfer function is given by
C(s)/ R(S) = G(s)/ 1+G(S) H(S)
Key takeaway
Parameter | Positive feedback | Negative Feedback |
Overall phase shift | 0 or 360  | 180  |
Input and Output Voltage , noise | Increases due to Feed back | Decreases due to Feed back |
Feedback Signal and Input signal | In phase | Out of phase |
Stability | Becomes poor | Becomes better |
Applications | Oscillators | Amplifiers |
Electrical System
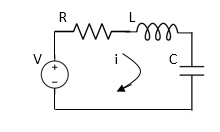
Fig. RLC Circuit
Example-1 For circuit shown above find value of current I?
Applying Kirchoff’s voltage Law
V= Ri +Ldi/dt +1/c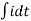
V= Rdq/dt + L d2q/dt2+q/c
Now By kirchoff’s current low
I= V/R+ 1/L 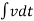 + cdv/dt
+ cdv/dt
But V= dø/dt
I= 1/R dø/dt + 1/L ø+cd2ø/dt2
But v= dø/dt
I= 1/R dø/dt+ 1/L. ø+c d2ø/dt2
Example-2 For the given mechanical system below draw the analogus system (force. Voltage)& find V0(s)/V1(s)
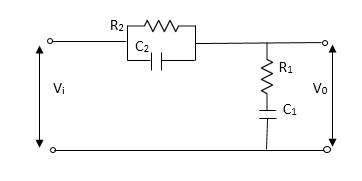
Soln.
Let Z1 = R2 11 1/c2
=R2*1/c2s/R2+1/c2s
Z1= R2/1+R2c2s
Let Z2 = R1+1/c1s
Z2= 1+R1c1s/c1s
V0(s)/vi(s) = z2/z1+z2
= 1+R1c1s/c1s/R2/1+R2c2s+1+R1c1s/c1s
V0(s)/v0(s) =(c1+R1c1s) (1+R2c2s)/R2c1s+1+sR1c1s2R1R2c1c2
Mechanical System
(a) Translational system
(b) Rotational system
Translational system
The motion that takes place along a straight line is called translational the forces that resist motion are
- Inertia: A body with mass ‘N’ acceleration ‘a’ will produce inertia fm(t)= malt N’ acceleration ‘a’ will produce inertia
fm(t)= M a(t)
In terms of velocity
Fm(t) = M dv(t)/dt
In terms of displacement
Fm(t)= Md2/dt2µt
- Damping force: The damping force is proportional to velocity for vis case function
F0(t) = B(t) = B dx(t) /dt
B Damping coefficient N/M sec
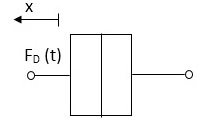
Fig. Damping Force
- Spring force: A spring stores potential energy. The releasing force of a string is proportional to the displacement.
Fk(t)  x(t)
x(t)
Fk(t) = k x (t)
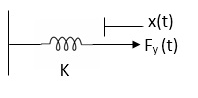
Fig. Spring Constant
Fk(t) = k 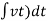
K = string constant N/m.
(b)Rational System: The motion of a body about a fixed axis is called as Rotational motion. The types of torques which can resist the motion are
i) Inertial Torque: The inertial torque is the product of moment of inertia I and angular acceleration.
TI(t) = J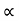 (t)
(t)
TI(t) = Jd/dt w(t)
TI(t) = Jd2ø(t)/dt2(N-m)
W (t) – Angular velocity
Ø(t) = Angular displacement
(ii) Damping Torque: it is product of damping efficient B and angular velocity w
T0 (t) = B w(t)
T0(t) = B d/dt ø(t)
(iii) Spring Torque: It is the product of torsional stiffness and angular displacement
Tø(t) = k ø(t)
K = N.m/rad
Fig. Rotational Spring Constant
D’Alembert’s Principle
For anybody, the algebraic sum of externally applied forces and the forces resisting motion in any given direction is zero.
Ex.
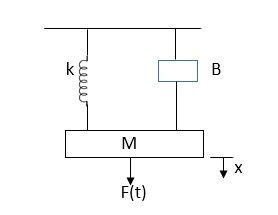
Fig. Mechanical System
In above figure applying D’Alemberts principle to write the equation of motion
As force f(t) acts downwards all other forces (of k,B,x)acts Opposite to it to considering f(t) as the and all other forces negative.
F(t)+fm (t) + fD(t) +fx(t) =0
f(t)- M d2x(t)/dt2+B dx(t)/dt +x(t)
Example-1 Draw the free body diagram and write the differential equation for system below.
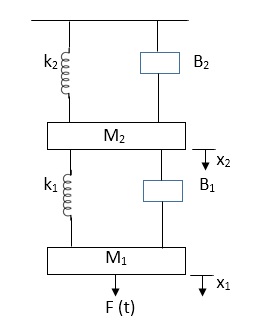
Soln: The free body diagram for M1 will be
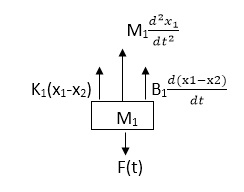
Fig. FBD for Mechanical System
F(t) = M1 d2/dt2x1+ B1 d/dt (x1-x2)+ k1(x1-x2)
Similarly for M2we have
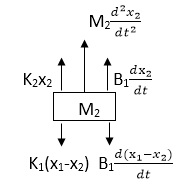
Fig. FBD for Mechanical System
K1(x1-x2) + B1d/dt(x1-x2) = k2x2+M2d2/dt2+B2dx2/dt
Thermal
Thermal systems are those that involve the transfer of heat from one substance to another. The model of thermal systems is obtained by using thermal resistance and capacitance which are the basic elements of the thermal system. The thermal resistance and capacitance are distributed in nature. But for simplicity in analysis lumped parameter models are used.
Consider a simple thermal system shown in the below figure. Let us assume that the tank is insulated to eliminate heat loss to the surrounding air, there is no heat storage in the insulation and liquid in the tank is kept at uniform temperature by perfect mixing with the help of a stirrer. Thus, a single temperature is used to describe the temperature of the liquid in the tank and of the out flowing liquid. The transfer function of thermal system can be derived as shown below.
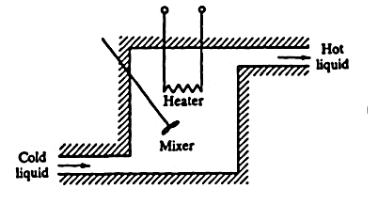
Fig. Thermal System
Let θ1 = Steady state temperature of inflowing liquid, °C
θ0 = Sandy state temperature of outflowing liquid, °C
G = Steady state liquid flow rate, Kg/sec
M = Mass of liquid in tank, Kg
c = Specific heat of liquid, Kcal/Kg °C
R = Thermal resistance, °C - sec/Kcal
C = Thermal capacitance, Kcal/°C
Q = Steady state heat input rate, Kcal/Sec
Let us assume that the temperature of inflowing liquid is kept constant. Let the heat input rate to the thermal system supplied by the heater is suddenly changed from Q to Q + q1. Due to this, the heat output flow rate will gradually change from Q to Q + q0. The temperature of the outflowing liquid will also be changed from θ0 to θ0 + θ.
For this system the equation for q0, C and R is obtained as follows,
Change in output heat flow rate 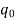 = Liquid flow rate, G × Specific heat of liquid, c × Change in temperature θ
= Liquid flow rate, G × Specific heat of liquid, c × Change in temperature θ

Thermal capacitance, C = Mass, M x Specific heat of liquid, c = Mc
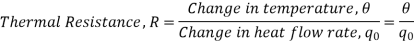 On substituting for qo from equation (1) in equation (3) we get,
On substituting for qo from equation (1) in equation (3) we get,
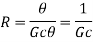
In this thermal system, rate of change of temperature is directly proportional to change in heat input rate.
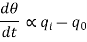

The constant of proportionality is capacitance C of the system.
Equation (5) is the differential equation governing system. Since, equation (5) is of first order equation, the system is first order system.
From equation (3) , R = θ/q0
q0 = θ/R
On substituting for q0 from equation (6) in equation (5) we get,

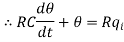
Let, L {θ} = θ(s); L{dθ/dt} = sθ(s) ; L{q1} = Q1(s)
On taking Laplace transform of equation (7)
RC s θ(s) + θ(s) = R Q1(s)
θ(s) [sRC + 1] = R Q1(s)
θ(s)/Q1(s) is the required transfer function of thermal system.
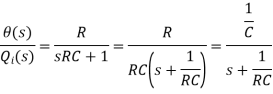
Hydraulic
The Hydraulic system of interest to control engineers may be classified into,
1.Liquid Level system
2.Hydraulic devices
The liquid level system consists of storage tanks and connecting pipes. The variables to be controlled are liquid height in tanks and flow rate in pipes. The driving force is the relative difference of the liquid heights in the tanks. The Hydraulic devices are devices using incompressible oil as their working medium. In this we will be learning transfer function of hydraulic system.
These devices are used for controlling the forces and motions. The driving force is the high-pressure oil supplied by the Hydraulic pumps. Liquids are slightly compressible at high pressures.
In hydraulic system, the compressibility effects may be neglected and conservation of volume is used as the basic physical law. The variables of hydraulic system are volumetric flow rate, q and pressure, R The volumetric flow rate, q is through variable and it is analogous to current. The pressure, P is across variable and it is analogous to voltage.
Three basic elements of hydraulic systems are the Resistance, Capacitance and inertance. The liquid flowing out of a tank can meet the resistance in several ways. Liquid while flowing through a pipe meet with resistance due to the friction between pipe walls and liquid. Presence of valves, bends, coupling of pipes of different diameter also offer resistance to liquid flow.
The capacitance is an energy storage element and it represents storage in gravity field. The inertance represents fluid inertia and is derived from the inertia forces required to accelerate the fluid in a pipe. It is also an energy storage element. But the energy storage due to inertance element is negligible compared to that of capacitance element.
Consider the flow through a short pipe connecting two tanks. The Resistance, R for liquid flow in such a pipe or restriction, is defined as the change in the level difference, necessary to cause a unit change in the flow rate.
R = Change in level difference/Change in flow rate
The Capacitance, C of a tank is defined to the change in quantity of stored liquid necessary to cause in the potential (head).
C = Change in liquid stored/Change in head
A simple liquid level system is shown in the below figure with steady flow rate, Q and steady state head, H.
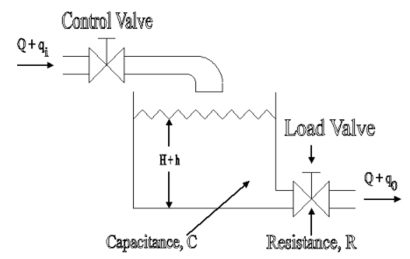
Fig. Liquid Level System
Let Q = Steady state flow rate(before any change has occured)
Qi = Small deviation of inflow rate from its steady-state value
Qo = Small deviation of outflow rate from its steady-state value
H = Steady state head (before any change has occurred)
h = Small deviation of head from its steady state value
Let the system be considered linear. The differential equation governing the system is obtained by equating the change in flow rate to the amount stored in the tank. In a small time interval dt, let the change in flow rate be (qi - qo) and the change in height be dh.
Now, Change In storage = Change in flow rate
C dh = (qi - qo) dh
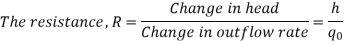
Qo = h/R
On substituting for qo, we get,
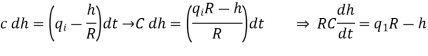 RC dh/dt + h = qi R
RC dh/dt + h = qi R
The above equation is the differential equation governing the system. The term RC is the time constant of the system .On the Laplace's transform of above equation we get,
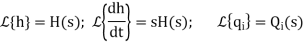
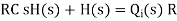
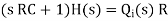

The above equation is the required transfer function of the Hydraulic system.
Analogy Between Electrical and Mechanical System:
Force -voltage | Force -current | Mechanical Translatory | Mechanical Rotational |
1.Voltage (v) | Current | Force (f) | Torque (T) |
2.Charge(q) | Flux (ø) | Displacement(x) | Angular Displacement(ø) |
3.current. | Voltage | Velocity v(t) | Angular velocity(w) |
4.Inductance(l) | Capacitance(c) | Mass (m) | Moment of inertia (J) |
5. Resistance(R) | Conductance G= (1/R) | Damping coefficient (B) | Damping Coefficient (B) |
6.Reciprocal of capacitance(1/c) | Inverse of Inductance (1/L) | Stiffness (K) | Stiffness(K) |
Key takeaway
Hydraulic fluid acts as a lubricant and coolant. Comparatively small sized hydraulic actuators can develop are forces or torques. Hydraulic actuators can be operated under continuous, intermittent, reversing, and called conditions without damage. Hydraulic actuators have a higher speed of response. They offer fast starts, stops and speed reversals. With availability of both linear and rotary actuators, the design has become more flexible.
Electrical and mechanical systems possess fixed analogy and there exist similarity between the equilibrium equations of the two. This allows forming such electrical systems whose behavioural characteristics are similar to the given mechanical system. Such systems are known as analogous systems.
Basically, two systems are analogous in nature when the conditions given below are fulfilled:
1. There must be two physically different systems.
2. There should have the same differential equation modelling of the systems.
The electrical analogous of mechanical translational can be obtained by
i) Force-Voltage Analogy (Loop Analysis)
Ii) Force-Current Analogy (Node Analysis)
i) Force-Voltage Analogy: If the dynamic characteristics of an electrical system is identical to that of a mechanical system, then the electrical system is said to be analogous to the mechanical system. This can be done by comparing the mathematical models of both the systems.
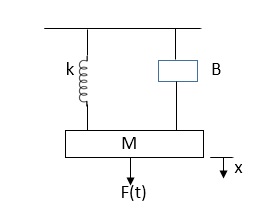
Fig. Mechanical System
The equation for above mechanical system is given by
f(t) = M  +B
+B 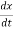 +kx (1)
+kx (1)
For series RLC circuit the mathematical equation is given as

Fig. Electrical System
V(t)= Ri + L 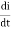 +
+ 
i = 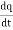
V(t) = L 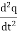 + R
+ R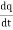 +
+  (2)
(2)
Comparing 1 and 2 we see that

This is shown in below table.
Ii) Force-Current Analogy:
For parallel RLC circuit shown below the KCL equation is written as
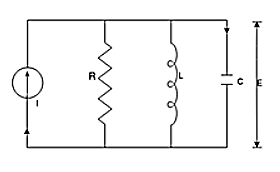
Fig. Electrical Circuit
i(t) = C 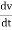 +
+  +
+ 
v = 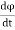
i(t) = C  + R
+ R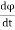 +
+ 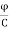 (3)
(3)
Comparing 1 and 3 we find that
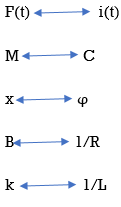
Electrical analogous to mechanical rotational systems
i) Torque-Voltage Analogy: Consider a mechanical rotational system as shown below
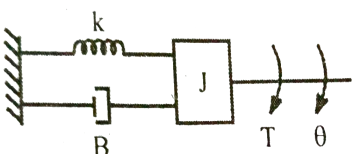
Fig. Mechanical system
The differential equation is then given by
T= J 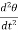 + B
+ B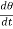 + kθ (4)
+ kθ (4)
And we already know the equation for series RLC circuit as in equation 2
V(t) = L + R
+ R 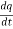 +
+
Comparing above equation 2 and 4 we have
T 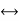 v
v
θ 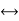 q
q
 i
i
B 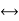 R
R
J 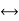 L
L
K  1/C
1/C
This is shown in below table.
Ii) Torque-Current Analogy: Consider the parallel RLC circuit as shown in above section. The equation for the circuit is already known to us given in (3)
i(t) = 
Comparing this equation with (4)
T i
i
J 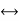 C
C
B 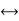 1/R
1/R
k 1/L
1/L
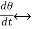 v
v
Generally, a function can be represented to its polynomial form. For example,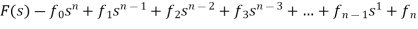 Now similarly transfer function of a control system can also be represented as
Now similarly transfer function of a control system can also be represented as
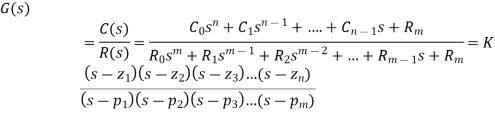
Where K is known as the gain factor of the transfer function.
Now in the above function if s = z1, or s = z2, or s = z3,….s = zn, the value of transfer function becomes zero. These z1, z2, z3,….zn, are roots of the numerator polynomial. As for these roots the numerator polynomial, the transfer function becomes zero, these roots are called zeros of the transfer function.
Now, if s = p1, or s = p2, or s = p3,….s = pm, the value of transfer function becomes infinite. Thus, the roots of denominator are called the poles of the function.
The transfer function of system is ratio of output to the input.
Advantages of Block diagram reduction technique:
- Very simple to Construct the Block diagram of complicated electrical & mechanical systems.
- The function of individual element can be visualized form block diagram
- Individual as well as overall performance of the system can be studied by the figure shown in Block diag.
- Overall CLTF can be easily calculated by Block diagram reduction rules.
Disadvantages of Block diagram reduction technique:
It does not include any information above physical construct of system (completely mathematical approach). Source of energy is generally not shown in the block diagram so diff. Block diagram can be drawn for the same function.
CLTf: -ve feedback
C(s)/R(s)= G(s)/1+G(s)H(s)
CLTF: +ve feedback
C(S)/R(S) = G(S)/1-G(s)H(S)
Rules of Block diagram Algebra:
Block in cascade

Moving summing point after a block
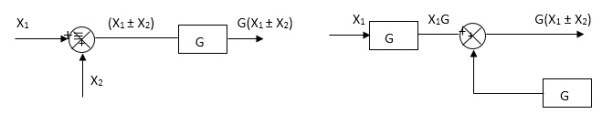
Moving summing point ahead of block

Moving take off point after a block
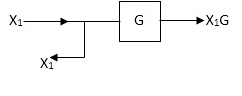
Moving take off point ahead a block
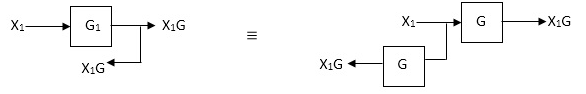
Eliminating a feedback Loop

Practice Problems
Q1. Reduce given B.D to canonical (simple form) and hence obtain the equivalent Tf = c(s)/ R(S)?

Sol:
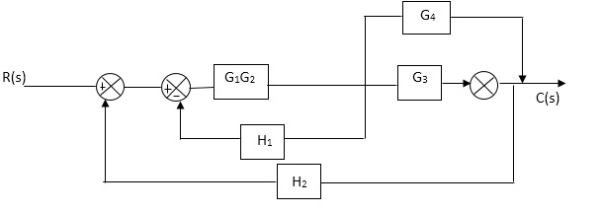
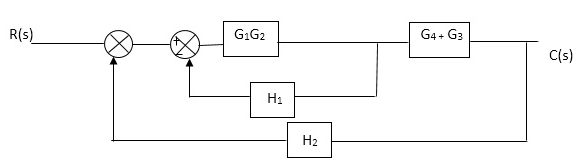
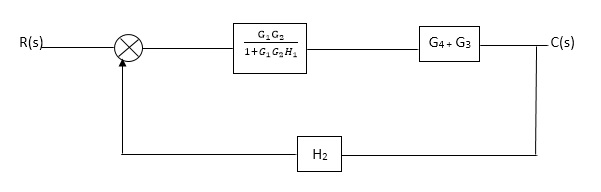
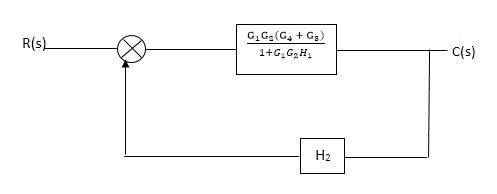
C(S)/R(S) = (G1G2) (G3+G4)/1+G1G2H1)/1-G1,G2(G3+G4) H2/1+G1G2H1
= G1G2(G3+G4)/1+G1G2H1-G1G2H2(G3+G4)
=G1G2(G3+G4)/1+(H1-H2)(G1G2) (G3+G4)
C(s)/R(S) = G1G2(G3+G4)/1+(H1-H2(G3+G4)) G1 G2
Q2) Reduce the Block diagram
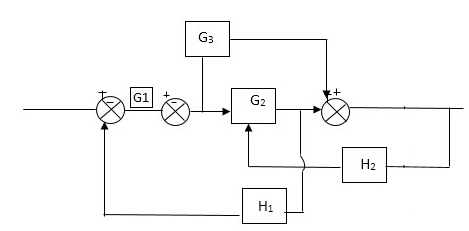
Sol:
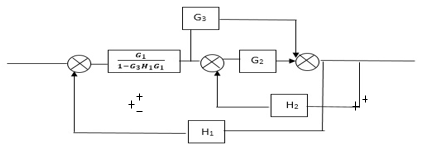

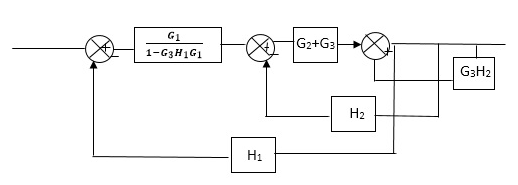
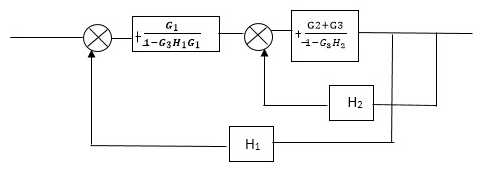
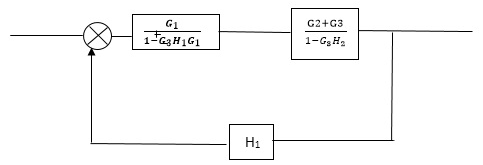
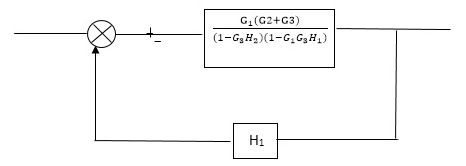
C(s)/R(s)= G1(G3+G2)/(1-G1G3X1) (1-G2X2) H1
= G(G3+G2)/(1-G3G1H1) (1-G2H2) + G1H1(G3+G2)
= G1(G3+G2)/1-G3G1H1-G2H2+G1H1(G3+G2H1
=G1(G3+G2)/1-G3H2+G1G2H1(1+G3H2)
As we already know that Block Diagram is represented as shown below
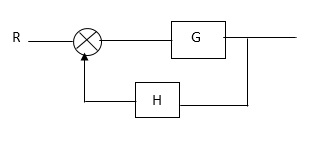
SFG
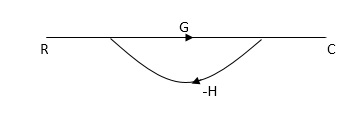
RULES:
1) The signal travels along a branch in the direction of an arrow.
2) The input signal is multiplied by the transmittance to obtain the o/p.
3) I/p signal at a node is sum of all the signals entering at that node.
4) A node transmits signal at all branches leaving that node.
Practice Problem
Q: For given block diagram draw the SFG?
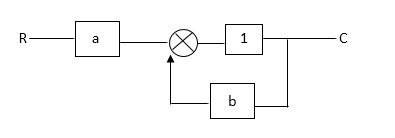


Ra+cb =c
c/R= a/1-b
Q. The SFG shown has forward path and singles isolated loop determine overall transmittance relating X3 and X1?
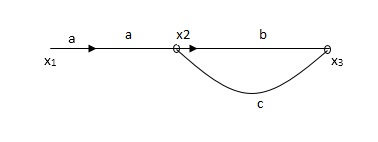
Soln:
X1- I/p node
X2-Intenmediale node
X3- o/p node
Ab- forward path (p)
Bc- 1 loop (L)
At node XQ:
X2 = x1a + x3c [Add i/p signals at node]
At node x3:
x2b =x3
(x1a+x3c) b = x3
X1ab = x3 (1-bc)
X1 = x3 (1-bc)/ab
Ab/(1-bc) = x3/x1
T= p/1-L

X1: I/p node x2, x3, x4, x5, Qnlexmedili node
X0: o/p node abdeg:- forward path
Bc, ef: Loop [isolated]
x2 = ax1+c x3
x3= bx2
x4 = d x3+f x5
x5 = e x4
x6= g x5
x6 = g(e x4) = ge [dx3+ e f x5]
xb = ge [d (bx2) + f (e x4)]
xb = ge [ db (ax1+cx3) + fe (dx3+ fx5)]
xb = ge [db (ax1+cb (ax1+x3) +fe[cdbx2]+
f(e [db (ax1+ cx3)
x2 = ax1 + cb (x2) x4 = d bx2 + f exq
x2 = ax1 + cbx2 = db (d4) + fe/1-cb
x2 = ax1/(1-cb) xy = db x2 + f x6/g
xy = db [ax1]/1-cb + f xb/g
x5 = c db ( ax1)/1-cb + efxb/g
xb = gx5
= gedb (ax1)/1-cb + g efxb/g
Xb = gx5
Gedb (ax1)/1-cb + g efxb/g
(1- gef/g) xb = gedb ax1/1-ab
Xb/x1 = gedb a/ (1- ef – bc + beef
Xb/x1 = p/ 1- (L1+L2) + L1 L2 for isolated loops
MASON’S GAIN FORMULA
T= 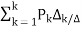
The overall transmittance Coverall gain can be determined by Masks formula.
Explanation
Pk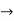 forward path transmittance of k+n path from a specified i/p node to n o/p nods
forward path transmittance of k+n path from a specified i/p node to n o/p nods
While calculating ipnode to n o/p nods.
While calculating ip no node should be encountered (used) more than ones.
 it is the graphics determined which involves of transmittances and multiple increases b/w non touching loops.
it is the graphics determined which involves of transmittances and multiple increases b/w non touching loops.
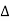 = 1- [sum of all individual loop transmitting]
= 1- [sum of all individual loop transmitting]
+[ sum of loop transmittance product of all possible non- touching loops]
-[sum of loop transmittance of all possible triples of non- touching loops]
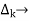 path factor associated with concerned path & involves all a in the graphic which are isolated from forward path under consideration.
path factor associated with concerned path & involves all a in the graphic which are isolated from forward path under consideration.
The path factor 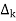 for kth is equal to graph determinant of SFG which effect after erasing the kth path from the graph
for kth is equal to graph determinant of SFG which effect after erasing the kth path from the graph
Q. Draw SFG for given block diagram?
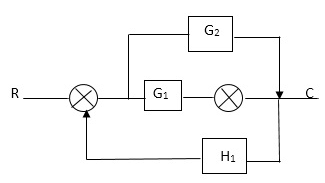
Sol:
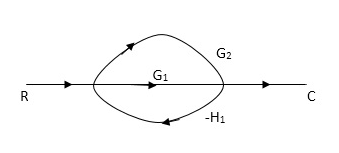
P1= G1 p2 =G2 Delta1 =1
L1= -G1 H1
 = 1-(-G1H1)
= 1-(-G1H1)
= 1+G1H1
T= G1+G2/1+G1H1
Q: Determine overall gain x5 and x1 Draw SFG
X2 = ax1+ f x2
X3= bx2 +exy
X4 = cx3+hx5
X5 =dx4 + gx2
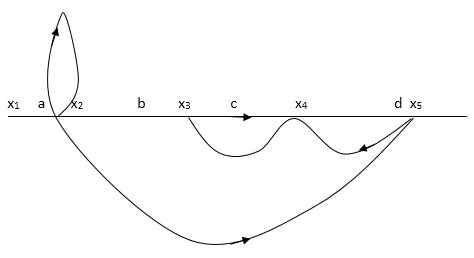
P1 = abcd p2 = ag
L1 = f L2 = ce, L3= dh
 1 = 1
1 = 1
 2= 1-ce
2= 1-ce
 = 1-[L2+L2+L3] + [L1 L2 +L1 L3]
= 1-[L2+L2+L3] + [L1 L2 +L1 L3]
= 1-[f+ le = dh] + [fce +fdh]
T= abcd+ ag (1-ce)/1-[ftce + dh ] + (fce + fdh)
Key takeaway
- The function of individual element can be visualized from block diagram
- The signal travels along a branch in the direction of an arrow.
- The input signal is multiplied by the transmittance to obtain the o/p.
References:
1. I. J. Nagrath and M. Gopal, “Control Systems Engineering”, New Age International, 2009.
2. K. Ogata, “Modern Control Engineering”, Prentice Hall, 1991
3. M. Gopal, “Control Systems: Principles and Design”, McGraw Hill Education, 1997.
4. B. C. Kuo, “Automatic Control System”, Prentice Hall, 1995.