Unit - 4

Laplace and z- Transforms

4.1 Review of Laplace Transform for Continuous Time Signals and Systems

Given a continuous-time signal x(t), the Laplace transform of x(t) is defined as

X(s) = 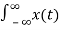  e -st dt -------------------------------------------------------(1)

X(s) is a function which takes complex numbers and returns complex number X(s) that is X(s) is function that maps the complex plane into the complex value.

The set of values of s for which the integral in (1) is well defined is called Region of Convergence.

Find the Laplace transform of e –t.

F(s) =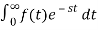

F(s)  =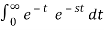  

F(s) =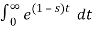

F(s) =  1 / 1-s [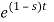]0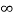

F (s = 1/ s-1.

Find the Laplace transform of unit -step function.

f(t) = 1 (t≥0)

F(s) = 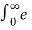  -st  dt   = -1/s  e -st   | 0 ∞    = 1/s [ e -∞ - e -0] = 1

F(s) = 1/s.

Find the Laplace transform of e-at u(t)

X(s) = 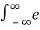  at u(t) e -st dt =  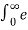 at  e -st dt  = –(s-a) t dt

= 1 – e –(s-a) ∞ / s-a

Key Takeaways:

This is the operator that transforms the signal in time domain in to a signal in a complex frequency domain called as ‘S’ domain. The complex frequency domain will be denoted by S and the complex frequency variable will be denoted by ‘s’

4.2 System functions

The response of an LTI system with impulse response h(t) to complex exponential input x(t) = e st is y(t) = H(s) e st  where s ia complex number and

H(s) = 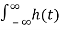  e -st dt

When s is purely imaginary this is Fourier transform H(jw)

When s is complex this is Laplace transform of h(t) , H(s )

Let z = r e jw     and z n = r n e jwn

Then for input z n we get output H(z) z n

Figure 1. I/O relationship

Here H(z) is called the system function.

y[n] = 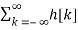  x[n-k]

= z n   z-k

Here z transform of h[k] is H[z].

Key Takeaways:

H(z) represents the Fourier transform

4.3 Poles and Zeros of System functions and Signals

Consider the difference equation given by

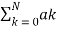  y[n-k] = 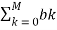x[n-k]

H(z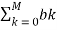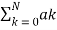) = z -k  /   z -k

Poles : H(z) -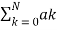 ∞ ;   z -k = 0 , z=0 if bo=0.

Zeros : H(z) -> 0 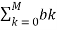   z -k =0

In factored form

H(z) = 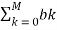z -k  /   z -k  = bo 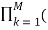1 – ck z-1 ) / ao 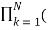1 – dk z-1 )

Here bo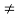0 , ao 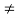0 .

Ck represents zeros denoted by “o”

Dk represents poles denoted by “x”

Example :

Find H(z), poles and zeros for the difference equation given by

y[n] – 3/8 y[n-1] – 7/16 y[n-2] = x[n] + x[n-2]

Solution:

Here ao=1,a1=-3/8,a2=-7/6,bo=1,b1=0,b2=1

H[z] = 1 + z -2 / 1 -3/8 z-1 -7/16 z -2

= (1+j z-1 ) (1 -jz-1)  / (1-7/8 z-1) ( 1+1/2 z-1)

Zeros : z=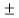j represented by o.

Poles z= 7/8 , z=-1/2  represented by x.

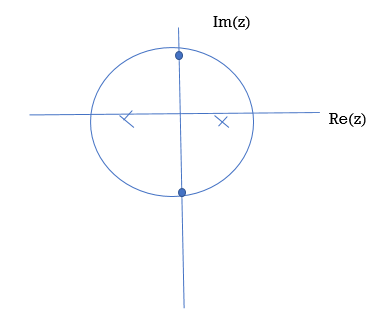
Figure 2. Poles and Zeros

Key Takeaways:

The poles of the system are indicated in the plot by an X while the zeros are indicated by a circle or O

4.4 Laplace domain analysis

Find io(t) using Laplace

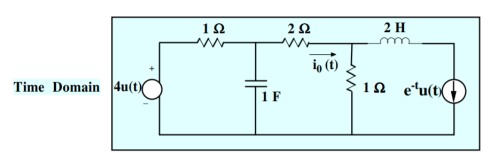
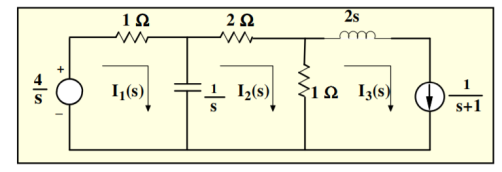
Figure 3. Mesh Network

Figure 4. Laplace network

Mesh 1:

(s+1)/s I1(s) – I2(s)/s = 4/s

(s+1) I1(s) – I2(s) = 4

Mesh 2:

-1/s I1(s) + 3s+1/s I2(s) – I3(s) =0

-1/s I1(s) + 3s+1/s I2(s) – 1/s+1 =0

-I1(s) + (3s+1) I2(s) = s/s+1

-(s+1) I1(s) + (s+1)(3s+1) I2(s) = s

Adding these two equations we get

S(3s+4) I2(s) = s+4

I2(s) = (1/3) (s+4)/ s(s+4/3) = 1/s -2/3/ s+4/3

i2(t) = [ 1-2/3 e -4/3 t ] u(t)

-I1(s) + 3s+1/s . [1/s -2/3 /s+4/3] =s/s+1

-I1(s) = s/s+1 – 3s+1/s[ 1/s -2/3/s+4/3]

Key Takeaways:

Laplace techniques convert circuits with voltage and current signals that change with time to the s-domain so you can analyse the circuit's action using only algebraic techniques.

4.5 Solution to differential equation and system behaviour

Using Laplce transform solve the differential equations :

y” – 3y’ -4y = -16x

y(0) = -4

y’(0) = -5

Apply the operator L to both sides of the differential equation; then use linearity, the initial conditions,

L[ y” – 3y’ -4y] = L[-16x]

L[ y”] – 3L[y’] -4L[y] = L[-16x]

[p 2 L[y] – p y’(0)] –[p L[y] – y[0]] – 4 L[y] = L[-16x]

p 2 L[y] +4p+5]-3[pL[y] +4] -4L[y]  = -16/p2

(p2 -3p-4) L[y] + 4p -7 = -16/p2

L[y] = -16/p2 -4p +7/p2 – 3p -4

But the partial fraction decomposition of this expression for L[ y] is

-16/p2 -4p+7/ p2 -3p-4 = -16/p2 -4p+7/ p2 -3p-4 = -16-4p3+7p2/ p2(p+1)(p-4)

= -3/p + 4/p2 +1/p+1 +-2/p-4

Therefore,

y= L-1 [-3/p + 4/p2 + 1/p+1+-2/p-4]

Which yields

y=-3 +4x+e-x -2 e 4x

Key Takeaways:

The first step in using Laplace transforms to solve an IVP is to take the transform of every term in the differential equation

4.6 The z-Transform for discrete time signals and systems

Given an analog signal x(t) the discrete time signal is represented by a sequence of weighted and delayed impulses.

Figure 5. Discrete time signal

A discrete time system is a mathematucal algorithm that takes an input sequence x[n] and produces output sequence y[n].

For any given sequence x[n] its z-transform is defined as :

X(z) = 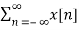  z -n

= …….+x[-2] z2 + x[-1] z1 + x[0] zo + x[1] z -1 + x[2] z -2 +……..

Where z is complex variable.

4.7 System functions

Given xn=un that is step function input to the system

G(z) = 1/(1-0.9z-1) Then output yn is given by

Y(z) = G(z) X(z)

X(z) = z(un) = 1/1-z-1

Y(z) = G(z) . 1/1-z-1

Yn = z-1(G(z) / 1-z-1) 

= z-1 ( 1/1-0.9 z-1 ). 1(1-z-1)

= 1/(1-0.9 z-1 )(1-z-1) = -0.9 / 1-0.9z-1 + 10/ 1-z-1

Yn = -9(0.9) n + 10

4.8 Poles and Zeros of systems and sequences

Poles are the values of z that make the denominator zero, and zeros are the values of z that make the numerator go to zero.

G(z) = 1/ 1+0.2 z-1 -0.48 z-2

= z 2/ z2 +0.2 z-0.48

= z2 / (z+0.8) (z-0.6)

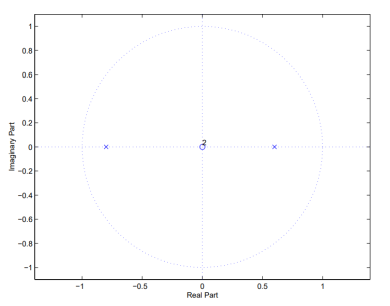
Figure 6. Poles and Zeros

4.8 Z domain analysis

Lets look at the system G(z)

G(z) = 1/1-az-1

The system has a pole at z=a and zero at z=0.

The impulse response of the system above is hn= an

Hence 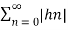  = 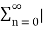a 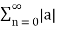n |= n.

For the system to be stable it must have finite sum. As 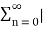a n represents geometric expression te sum is finite if and only if |a|<1.

That means that the POLE must be within the unit circle!

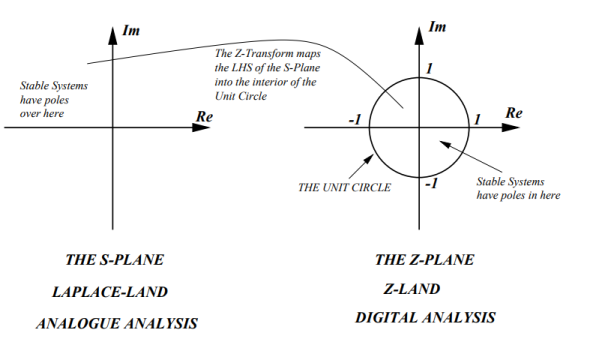
Figure 7. s-plane to z-plane

Key Takeaways:

The Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation. 

References:

1. Signals and Systems by Simon Haykin
2. Signals and Systems by Ganesh Rao
3. Signals and Systems by P. Ramesh Babu
4. Signals and Systems by Chitode

Unit - 4

Laplace and z- Transforms

4.1 Review of Laplace Transform for Continuous Time Signals and Systems

Given a continuous-time signal x(t), the Laplace transform of x(t) is defined as

X(s) = 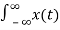  e -st dt -------------------------------------------------------(1)

X(s) is a function which takes complex numbers and returns complex number X(s) that is X(s) is function that maps the complex plane into the complex value.

The set of values of s for which the integral in (1) is well defined is called Region of Convergence.

Find the Laplace transform of e –t.

F(s) =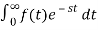

F(s)  =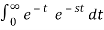  

F(s) =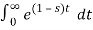

F(s) =  1 / 1-s [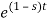]0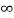

F (s = 1/ s-1.

Find the Laplace transform of unit -step function.

f(t) = 1 (t≥0)

F(s) = 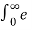  -st  dt   = -1/s  e -st   | 0 ∞    = 1/s [ e -∞ - e -0] = 1

F(s) = 1/s.

Find the Laplace transform of e-at u(t)

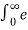X(s) =   at u(t) e -st dt =   at  e -st dt  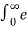= –(s-a) t dt

= 1 – e –(s-a) ∞ / s-a

Key Takeaways:

This is the operator that transforms the signal in time domain in to a signal in a complex frequency domain called as ‘S’ domain. The complex frequency domain will be denoted by S and the complex frequency variable will be denoted by ‘s’

4.2 System functions

The response of an LTI system with impulse response h(t) to complex exponential input x(t) = e st is y(t) = H(s) e st  where s ia complex number and

H(s) = 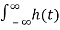  e -st dt

When s is purely imaginary this is Fourier transform H(jw)

When s is complex this is Laplace transform of h(t) , H(s )

Let z = r e jw     and z n = r n e jwn

Then for input z n we get output H(z) z n

Figure 1. I/O relationship

Here H(z) is called the system function.

y[n] = 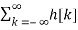  x[n-k]

= z n 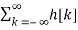  z-k

Here z transform of h[k] is H[z].

Key Takeaways:

H(z) represents the Fourier transform

4.3 Poles and Zeros of System functions and Signals

Consider the difference equation given by

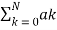  y[n-k] = x[n-k]

H(z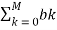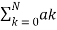) = z -k  /   z -k

Poles : H(z) -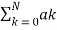 ∞ ;   z -k = 0 , z=0 if bo=0.

Zeros : H(z) -> 0    z -k =0

In factored form

H(z) = 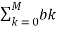z -k  /   z -k  = bo 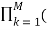1 – ck z-1 ) / ao 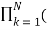1 – dk z-1 )

Here bo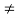0 , ao 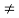0 .

Ck represents zeros denoted by “o”

Dk represents poles denoted by “x”

Example :

Find H(z), poles and zeros for the difference equation given by

y[n] – 3/8 y[n-1] – 7/16 y[n-2] = x[n] + x[n-2]

Solution:

Here ao=1,a1=-3/8,a2=-7/6,bo=1,b1=0,b2=1

H[z] = 1 + z -2 / 1 -3/8 z-1 -7/16 z -2

= (1+j z-1 ) (1 -jz-1)  / (1-7/8 z-1) ( 1+1/2 z-1)

Zeros : z=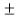j represented by o.

Poles z= 7/8 , z=-1/2  represented by x.

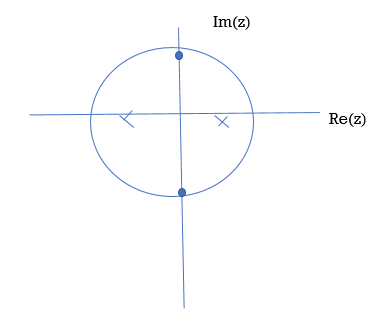
Figure 2. Poles and Zeros

Key Takeaways:

The poles of the system are indicated in the plot by an X while the zeros are indicated by a circle or O

4.4 Laplace domain analysis

Find io(t) using Laplace

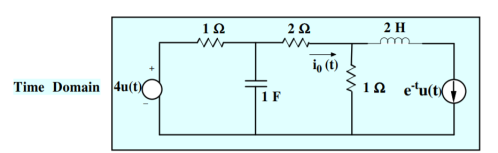
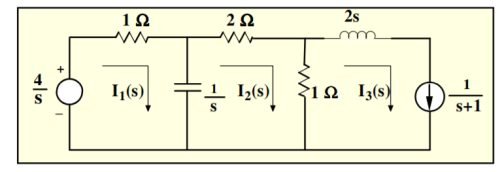
Figure 3. Mesh Network

Figure 4. Laplace network

Mesh 1:

(s+1)/s I1(s) – I2(s)/s = 4/s

(s+1) I1(s) – I2(s) = 4

Mesh 2:

-1/s I1(s) + 3s+1/s I2(s) – I3(s) =0

-1/s I1(s) + 3s+1/s I2(s) – 1/s+1 =0

-I1(s) + (3s+1) I2(s) = s/s+1

-(s+1) I1(s) + (s+1)(3s+1) I2(s) = s

Adding these two equations we get

S(3s+4) I2(s) = s+4

I2(s) = (1/3) (s+4)/ s(s+4/3) = 1/s -2/3/ s+4/3

i2(t) = [ 1-2/3 e -4/3 t ] u(t)

-I1(s) + 3s+1/s . [1/s -2/3 /s+4/3] =s/s+1

-I1(s) = s/s+1 – 3s+1/s[ 1/s -2/3/s+4/3]

Key Takeaways:

Laplace techniques convert circuits with voltage and current signals that change with time to the s-domain so you can analyse the circuit's action using only algebraic techniques.

4.5 Solution to differential equation and system behaviour

Using Laplce transform solve the differential equations :

y” – 3y’ -4y = -16x

y(0) = -4

y’(0) = -5

Apply the operator L to both sides of the differential equation; then use linearity, the initial conditions,

L[ y” – 3y’ -4y] = L[-16x]

L[ y”] – 3L[y’] -4L[y] = L[-16x]

[p 2 L[y] – p y’(0)] –[p L[y] – y[0]] – 4 L[y] = L[-16x]

p 2 L[y] +4p+5]-3[pL[y] +4] -4L[y]  = -16/p2

(p2 -3p-4) L[y] + 4p -7 = -16/p2

L[y] = -16/p2 -4p +7/p2 – 3p -4

But the partial fraction decomposition of this expression for L[ y] is

-16/p2 -4p+7/ p2 -3p-4 = -16/p2 -4p+7/ p2 -3p-4 = -16-4p3+7p2/ p2(p+1)(p-4)

= -3/p + 4/p2 +1/p+1 +-2/p-4

Therefore,

y= L-1 [-3/p + 4/p2 + 1/p+1+-2/p-4]

Which yields

y=-3 +4x+e-x -2 e 4x

Key Takeaways:

The first step in using Laplace transforms to solve an IVP is to take the transform of every term in the differential equation

4.6 The z-Transform for discrete time signals and systems

Given an analog signal x(t) the discrete time signal is represented by a sequence of weighted and delayed impulses.

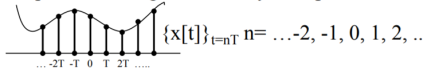
Figure 5. Discrete time signal

A discrete time system is a mathematucal algorithm that takes an input sequence x[n] and produces output sequence y[n].

For any given sequence x[n] its z-transform is defined as :

X(z) = 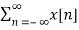  z -n

= …….+x[-2] z2 + x[-1] z1 + x[0] zo + x[1] z -1 + x[2] z -2 +……..

Where z is complex variable.

4.7 System functions

Given xn=un that is step function input to the system

G(z) = 1/(1-0.9z-1) Then output yn is given by

Y(z) = G(z) X(z)

X(z) = z(un) = 1/1-z-1

Y(z) = G(z) . 1/1-z-1

Yn = z-1(G(z) / 1-z-1) 

= z-1 ( 1/1-0.9 z-1 ). 1(1-z-1)

= 1/(1-0.9 z-1 )(1-z-1) = -0.9 / 1-0.9z-1 + 10/ 1-z-1

Yn = -9(0.9) n + 10

4.8 Poles and Zeros of systems and sequences

Poles are the values of z that make the denominator zero, and zeros are the values of z that make the numerator go to zero.

G(z) = 1/ 1+0.2 z-1 -0.48 z-2

= z 2/ z2 +0.2 z-0.48

= z2 / (z+0.8) (z-0.6)

Figure 6. Poles and Zeros

4.8 Z domain analysis

Lets look at the system G(z)

G(z) = 1/1-az-1

The system has a pole at z=a and zero at z=0.

The impulse response of the system above is hn= an

Hence 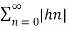  = 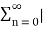a 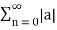n |= n.

For the system to be stable it must have finite sum. As 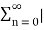a n represents geometric expression te sum is finite if and only if |a|<1.

That means that the POLE must be within the unit circle!

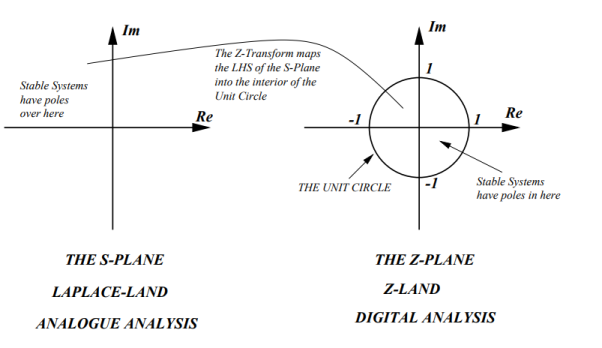
Figure 7. s-plane to z-plane

Key Takeaways:

The Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation. 

References:

1. Signals and Systems by Simon Haykin
2. Signals and Systems by Ganesh Rao
3. Signals and Systems by P. Ramesh Babu
4. Signals and Systems by Chitode