Unit - 1
Introduction
The communication that occurs in our day-to-day life is in the form of signals. These signals, such as sound signals, generally, are analog in nature. When the communication needs to be established over a distance, then the analog signals are sent through wire, using different techniques for effective transmission.
The Necessity of Digitization
The conventional methods of communication used analog signals for long distance communications, which suffer from many losses such as distortion, interference, and other losses including security breach.
In order to overcome these problems, the signals are digitized using different techniques. The digitized signals allow the communication to be more clear and accurate without losses.
The following figure indicates the difference between analog and digital signals. The digital signals consist of 1s and 0s which indicate High and Low values respectively.
Fig 1
The elements which form a digital communication system is represented by the following block diagram for the ease of understanding.
Fig 2 Elements of Digital Communication System
Following are the sections of the digital communication system.
Source
The source can be an analog signal.
Example: A Sound signal
Input Transducer
This is a transducer which takes a physical input and converts it to an electrical signal. This block also consists of an analog to digital converter where a digital signal is needed for further processes.
A digital signal is generally represented by a binary sequence.
Source Encoder
The source encoder compresses the data into minimum number of bits. This process helps in effective utilization of the bandwidth. It removes the redundant bits unnecessary excess bits, i.e. ,zeroes.
Channel Encoder
The channel encoder, does the coding for error correction. During the transmission of the signal, due to the noise in the channel, the signal may get altered and hence to avoid this, the channel encoder adds some redundant bits to the transmitted data. These are the error correcting bits.
Digital Modulator
The signal to be transmitted is modulated here by a carrier. The signal is also converted to analog from the digital sequence, in order to make it travel through the channel or medium.
Channel
The channel or a medium, allows the analog signal to transmit from the transmitter end to the receiver end.
Digital Demodulator
This is the first step at the receiver end. The received signal is demodulated as well as converted again from analog to digital. The signal gets reconstructed here.
Channel Decoder
The channel decoder, after detecting the sequence, does some error corrections. The distortions which might occur during the transmission, are corrected by adding some redundant bits. This addition of bits helps in the complete recovery of the original signal.
Source Decoder
The resultant signal is once again digitized by sampling and quantizing so that the pure digital output is obtained without the loss of information. The source decoder recreates the source output.
Output Transducer
This is the last block which converts the signal into the original physical form, which was at the input of the transmitter. It converts the electrical signal into physical output.
Output Signal
This is the output which is produced after the whole process.
Key takeaway
The channel decoder, after detecting the sequence, does some error corrections. The distortions which might occur during the transmission, are corrected by adding some redundant bits.
In Pulse Code Modulation, the message signal is represented by a sequence of coded pulses. This message signal is achieved by representing the signal in discrete form in both time and amplitude.
Basic Elements of PCM
The transmitter section comprises of Sampling, Quantizing and Encoding. The low pass filter prior to sampling prevents aliasing of the message signal.
The basic operations in the receiver section are regeneration of impaired signals, decoding, and reconstruction of the quantized pulse train.
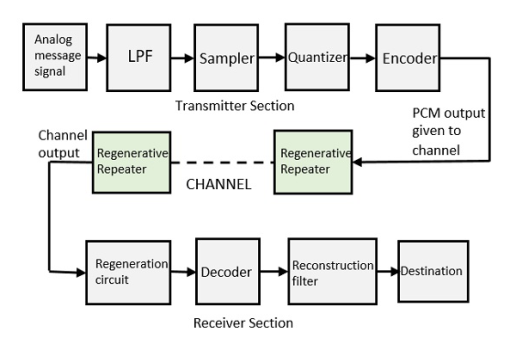
Fig. 3: PCM
Low Pass Filter
This filter eliminates the high frequency components present in the input analog signal to avoid aliasing of the message signal.
Sampler
It helps to collect the sample data at instantaneous values of message signal, so as to reconstruct the original signal. The sampling rate must be in accordance with the sampling theorem.
Quantizer
It reduces excessive bits and confines the data. It reduces the redundant bits and compresses the value of the sampled output.
Encoder
The digitization of analog signal is done by the encoder. It designates each quantized level by a binary code. Encoding minimizes the bandwidth used.
Regenerative Repeater
It increases the signal strength. The output of the channel also has one regenerative repeater circuit, to compensate the signal loss and reconstruct the signal, and also to increase its strength.
Decoder
The decoder circuit decodes the pulse coded waveform to reproduce the original signal. This circuit acts as the demodulator.
Reconstruction Filter
After the digital-to-analog conversion is done by the regenerative circuit and the decoder, a low-pass filter is employed, called as the reconstruction filter to get back the original signal.
Hence, the Pulse Code Modulator circuit digitizes the given analog signal, codes it and samples it, and then transmits it in an analog form. This whole process is repeated in a reverse pattern to obtain the original signal.
Quantization noise is a model of quantization error introduced by quantization in the analog-to-digital conversion (ADC). It is a rounding error between the analog input voltage to the ADC and the output digitized value. The noise is non-linear and signal-dependent.
There are two types of Quantization - Uniform Quantization and Non-uniform Quantization.
The type of quantization in which the quantization levels are uniformly spaced is termed as a Uniform Quantization. The type of quantization in which the quantization levels are unequal and mostly the relation between them is logarithmic, is termed as a Non-uniform Quantization.
It is a combination of Compressing and Expanding, which means that it does both. This is a non-linear technique used in PCM which compresses the data at the transmitter and expands the same data at the receiver. The effects of noise and crosstalk are reduced by using this technique.
There are two types of Companding techniques. They are −
A-law Companding Technique
- Uniform quantization is achieved at A = 1, where the characteristic curve is linear and no compression is done.
- A-law has mid-rise at the origin. Hence, it contains a non-zero value.
- A-law companding is used for PCM telephone systems.
µ-law Companding Technique
- Uniform quantization is achieved at µ = 0, where the characteristic curve is linear and no compression is done.
- µ-law has mid-tread at the origin. Hence, it contains a zero value.
- µ-law companding is used for speech and music signals.
µ-law is used in North America and Japan.
Differential pulse code modulation (DPCM) is a procedure of converting an analog into a digital signal in which an analog signal is sampled and then the difference between the actual sample value and its predicted value (predicted value is based on previous sample or samples) is quantized and then encoded forming a digital value.
DPCM code words represent differences between samples unlike PCM where code words represented a sample value.
Basic concept of DPCM - coding a difference, is based on the fact that most source signals show significant correlation between successive samples so encoding uses redundancy in sample values which implies lower bit rate.
Realization of basic concept (described above) is based on a technique in which we have to predict current sample value based upon previous samples (or sample) and we have to encode the difference between actual value of sample and predicted value (the difference between samples can be interpreted as prediction error).
Because it's necessary to predict sample value DPCM is form of predictive coding.
DPCM compression depends on the prediction technique, well-conducted prediction techniques lead to good compression rates, in other cases DPCM could mean expansion comparing to regular PCM encoding.
Fig. 4: DPCM
Key Takeaways:
- DPCM code words represent differences between samples unlike PCM where code words represented a sample value.
- Basic concept of DPCM - coding a difference, is based on the fact that most source signals show significant correlation between successive samples so encoding uses redundancy in sample values which implies lower bit rate.
The type of modulation, where the sampling rate is much higher and in which the step size after quantization is of a smaller value Δ, such a modulation is termed as delta modulation.
Features
- The quality is moderate.
- The design of the modulator and the demodulator is simple.
- The stair-case approximation of output waveform.
- The step-size is very small, i.e., Δ delta.
- The bit rate can be decided by the user.
- This involves simpler implementation.
Delta Modulation is a simplified form of DPCM technique, also viewed as 1-bit DPCM scheme. As the sampling interval is reduced, the signal correlation will be higher.
Delta Modulator
The Delta Modulator comprises of a 1-bit quantizer and a delay circuit along with two summer circuits. Following is the block diagram of a delta modulator.
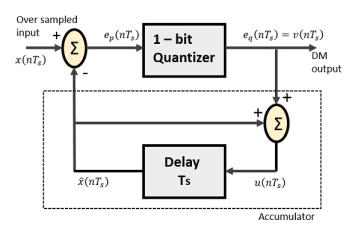
Fig. 5
The predictor circuit in DPCM is replaced by a simple delay circuit in DM.
From the above diagram, we have the notations as −
- x(nTs)= over sampled input
- Ep(nTs) = summer output and quantizer input
- Eq(nTs) = quantizer output = v(nTs)
- xˆ(nTs) = output of delay circuit
- u(nTs) = input of delay circuit
Using these notations, now we shall try to figure out the process of delta modulation.
Ep(nTs)=x(nTs)−xˆ(nTs) ---------equation 1
=x(nTs)−u([n−1]Ts
=x(nTs)−[xˆ[[n−1]Ts]+v[[n−1]Ts]] -------equation 2
Further,
v(nTs)=eq(nTs)=S.sig.[ep(nTs)] ---------equation 3
u(nTs)=xˆ(nTs)+eq(nTs)
Where,
- xˆ(nTs) = the previous value of the delay circuit
- Eq(nTs) = quantizer output = v(nTs)
Hence,
u(nTs)=u([n−1]Ts)+v(nTs) ---------equation 4
Which means,
The present input of the delay unit
= The previous output of the delay unit + the present quantizer output the present quantizer output
Assuming zero condition of Accumulation,
Accumulated version of DM output = 
--------equation 5
Now, note that
=
---------equation 6
Delay unit output is an Accumulator output lagging by one sample.
From equations 5 & 6, we get a possible structure for the demodulator.
A Stair-case approximated waveform will be the output of the delta modulator with the step-size as delta (Δ). The output quality of the waveform is moderate.
Delta Demodulator
The delta demodulator comprises of a low pass filter, a summer, and a delay circuit. The predictor circuit is eliminated here and hence no assumed input is given to the demodulator.
Following is the diagram for delta demodulator.
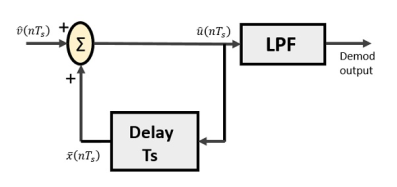
Fig. 6
From the above diagram, we have the notations as −
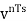is the input sample
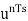is the summer output
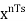is the delayed output
A binary sequence will be given as an input to the demodulator. The stair-case approximated output is given to the LPF.
Low pass filter is used for many reasons, but the prominent reason is noise elimination for out-of-band signals. The step-size error that may occur at the transmitter is called granular noise, which is eliminated here. If there is no noise present, then the modulator output equals the demodulator input.
Advantages of DM Over DPCM
- 1-bit quantizer
- Very easy design of the modulator and the demodulator
However, there exists some noise in DM.
- Slope Over load distortion (when Δ is small)
- Granular noise (when Δ is large)
In digital modulation, we have come across certain problem of determining the step-size, which influences the quality of the output wave.
A larger step-size is needed in the steep slope of modulating signal and a smaller step size is needed where the message has a small slope. The minute details get missed in the process. So, it would be better if we can control the adjustment of step-size, according to our requirement in order to obtain the sampling in a desired fashion. This is the concept of Adaptive Delta Modulation.
Following is the block diagram of Adaptive delta modulator.
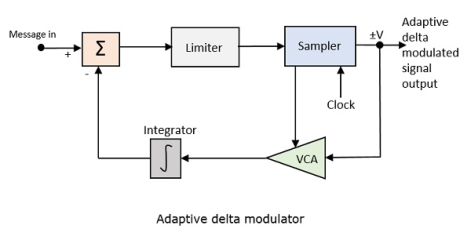
Fig. 7 Adaptive delta modulator
The gain of the voltage-controlled amplifier is adjusted by the output signal from the sampler. The amplifier gain determines the step-size and both are proportional.
ADM quantizes the difference between the value of the current sample and the predicted value of the next sample. It uses a variable step height to predict the next values, for the faithful reproduction of the fast-varying values.
Key takeaway
ADM quantizes the difference between the value of the current sample and the predicted value of the next sample. It uses a variable step height to predict the next values
- Delta-sigma (ΔΣ; or sigma-delta, ΣΔ) modulation is a method for encoding analog signals into digital signals as found in an analog-to-digital converter (ADC).
- It is used to convert high bit-count, low-frequency digital signals into lower bit-count, higher-frequency digital signals as part of the process to convert digital signals into analog as part of a digital-to-analog converter (DAC).
- In this, accuracy of the modulation is improved by passing the digital output through a 1-bit DAC and adding (sigma) the resulting analog signal to the input signal, thereby reducing the error introduced by the delta modulation.
- Both ADCs and DACs can employ delta-sigma modulation.
- A delta-sigma ADC first encodes an analog signal using high-frequency delta-sigma modulation, and then applies a digital filter to form a higher-resolution but lower sample-frequency digital output.
- A delta-sigma DAC encodes a high-resolution digital input signal into a lower-resolution but higher sample-frequency signal that is mapped to voltages, and then smoothed with an analog filter.
- In both cases, the temporary use of a lower-resolution signal simplifies circuit design and improves efficiency.
- Primarily because of its cost efficiency and reduced circuit complexity, it is used in modern electronic components such as DACs, ADCs, frequency synthesizers, switched-mode power supplies and motor controllers.
Fig. 8
Linear Predictive Coding (LPC) is known to be a method that is used in the process of speech coding as well as the synthesis of the same. One can verify the different storage galleries that come into play during the entire process. These processes are used to give accurate estimations that are used in order to keep the efficiency of the whole process higher.
One can use this method specifically in order to get samples that have been used in as a combination to get the value of the next prediction. This is used for the purpose of recognition. We can see this with the help of an equation.
for some value of p,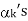
We can solve the LPC equations with different types of methods which are given as:
Covariance Method
Autocovariance Method
Inner Product Method
Spectral Estimation Method
Maximum Likelihood Method
Lattice Method
Basic Principles of LPC
There is a filter that is based on the variance of time that helps note down the pulse shapes as well as the different types of forms.
There is also a train that is based on the impulse generator from voice or noise recognition.
We can see a representation of this given below. This model is also known as the “all-pole model”.
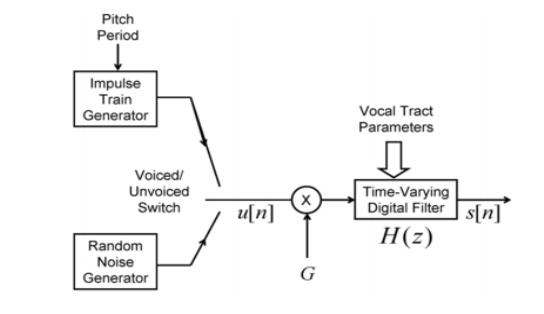
Fig. 9
Key Takeaways:
Linear Predictive Coding (LPC) is known to be a method that is used in the process of speech coding as well as the synthesis of the same.
References:
1. B.P. Lathi, “Modern Digital and Analog communication Systems”, 4th Edition, Oxford University Press, 2010.
2. Rishabh Anand, Communication Systems, Khanna Publishing House, Delhi.
3. S.Haykin, Digital Communications, John Wiley & Sons, 2009.
4. B.Sklar, Digital Communications, 2nd Edition, Pearson Education, New Delhi, 2009.
5. John G.Proakis, Digital Communications, 3rd edition, McGraw Hill, 1995.
