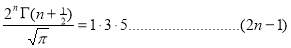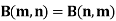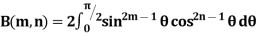Unit - 2
Reduction formula for integrals
Reduction formula for: 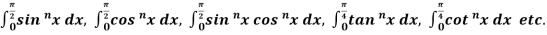
What is reduction formula?
A formula of the form,
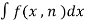 = g(x) +
= g(x) + 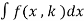
Where k<n, is called a reduction formula.
(a). Reduction formula for 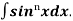
Let, Iⁿ = 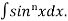 =
=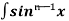 sinxdx , if n>1
sinxdx , if n>1
Taking 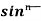 ¹x as first function and sinx as second function, integrate by parts,
¹x as first function and sinx as second function, integrate by parts,
Iⁿ = -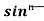 ¹x cosx – (n -1)
¹x cosx – (n -1)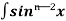 cosx(-cosx)dx
cosx(-cosx)dx
= - ¹x cosx + (n - 1)
¹x cosx + (n - 1)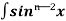 cos²xdx
cos²xdx
= -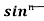 ¹x cosx + (n - 1)
¹x cosx + (n - 1)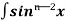 ( 1 - sin²x) dx
( 1 - sin²x) dx
= -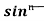 ¹x cosx + (n - 1)
¹x cosx + (n - 1)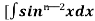 -
- 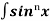 dx
dx
= -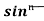 ¹x cosx + (n - 1) [ Iⁿ ‾ ² - Iⁿ]
¹x cosx + (n - 1) [ Iⁿ ‾ ² - Iⁿ]
By solving above
Iⁿ = +
+ 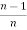 Iⁿ‾²
Iⁿ‾²
This is the reduction formula for 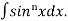
Example: Evaluate 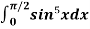 by using reduction formula.
by using reduction formula.
Solution: we know that,
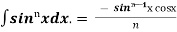 +
+ 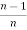 Iⁿ‾², here Iⁿ‾² =
Iⁿ‾², here Iⁿ‾² = 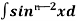
Now using this formula,
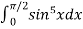 =
=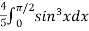
= 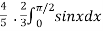
= 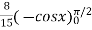
= 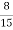
(b). Reduction formula for 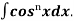
Similarly we can get the formula for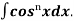
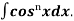 =
= 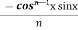 +
+ 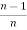 Iⁿ‾²
Iⁿ‾²
We can use the following formulas to get the result easily,
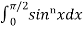 =
= 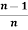 .
.  .
.  , only if n is odd and n ≥3
, only if n is odd and n ≥3
=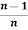 .
.  .
.  .
.  , only if n is even and n ≥2
, only if n is even and n ≥2
We apply same formula for cos x.
Example2: evaluate 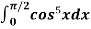 .
.
Solution: we will apply reduction formula to evaluate,
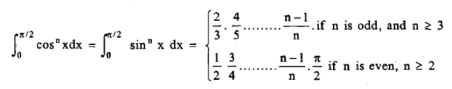
So, here n = 5, which is odd, we will get ,
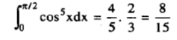
(C) Reduction formula for: 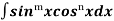
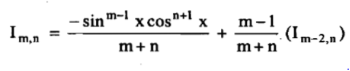
Where
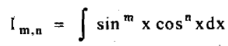
Example1: Evaluate 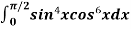 by using reduction formula.
by using reduction formula.
Solution: here, m = 4, n = 6,
Now we will apply above reduction formula,
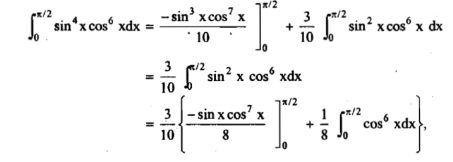
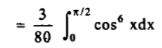
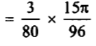
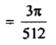
Example2: Evaluate 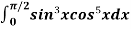 by using reduction formula.
by using reduction formula.
Solution: Here we can see that, m = 3 and n = 5,
Now we will apply reduction formula,
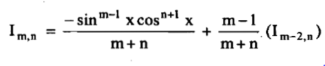

(D) Reduction formula for 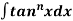 and
and 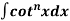
Let
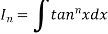

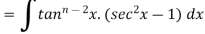
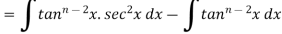
Thus, the required reduction formula is-

And for 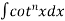 , the reduction formula will be-
, the reduction formula will be-
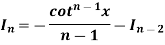
Example: Evaluate 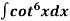 by using reduction formula.
by using reduction formula.
Sol.
Put n = 6, 4, and 2 successively in the reduction formula for 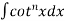 , we obtain-
, we obtain-

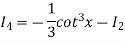
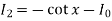
Thus
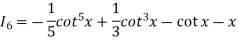
Example: If 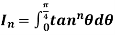 then prove that
then prove that 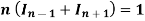
Sol.
The reduction formula for 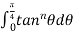 is-
is-

On changing n to n+1, we get-
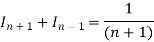
Or

Hence proved
Key takeaways-
- Iⁿ =
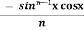 +
+ 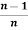 Iⁿ‾²
Iⁿ‾² 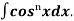 =
= 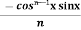 +
+ 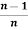 Iⁿ‾²
Iⁿ‾²
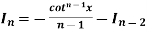
Improper integrals
(1) Let f is function defined on [a, ∞) and it is integrable on [a, t] for all t >a, then
If 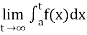 exists, then we define the improper integral of f over [a, ∞) as follows-
exists, then we define the improper integral of f over [a, ∞) as follows-
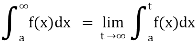
(2) Let f is function defined on (-∞,b] and it is integrable on [t, b] for all t >b, then
If 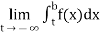 exists, then we define the improper integral of f over (-∞, b] as follows-
exists, then we define the improper integral of f over (-∞, b] as follows-

(3) Let f is function defined on (-∞, ∞] and it is integrable on [a, b] for every closed and bounded interval [a, b] which is the subset of R., then
If 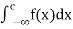 and
and 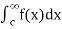 exist for some c belongs to R, then we define the improper integral of f over (-∞,∞) as follows-
exist for some c belongs to R, then we define the improper integral of f over (-∞,∞) as follows-
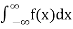 =
= 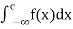 +
+ 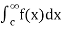
(4) Let f is function defined on (a,∞) and 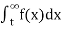 exists for all t>a, then
exists for all t>a, then
If 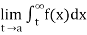 exists, then we define the improper integral of f over (a ∞) as follows-
exists, then we define the improper integral of f over (a ∞) as follows-
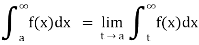
(5) Let f is function defined on (-∞, b) and 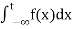 exists for all t<b, then
exists for all t<b, then
If  exists, then we define the improper integral of f over (-∞, b) as follows-
exists, then we define the improper integral of f over (-∞, b) as follows-
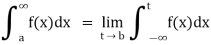
Improper integrals over finite intervals-
(1) Let f is function defined on (a, b] and  exists for all t ∈ (a,b), then
exists for all t ∈ (a,b), then
If 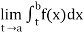 exists, then we define the improper integral of f over (a, b] as follows-
exists, then we define the improper integral of f over (a, b] as follows-
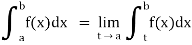
(2) Let f is function defined on [a, b) and 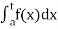 exists for all t ∈ (a,b), then
exists for all t ∈ (a,b), then
If 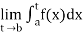 exists, then we define the improper integral of f over [a, b) as follows-
exists, then we define the improper integral of f over [a, b) as follows-
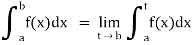
(3) Let f is function defined on [a, c) and (c, b]. If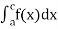 and
and 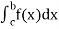 exist
exist
Then we define the improper integral of f over [a, b] as follows-
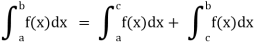
When we apply limits in indefinite integrals are called definite integrals.
If an expression is written as  , here ‘b’ is called upper limit and ‘a’ is called lower limit.
, here ‘b’ is called upper limit and ‘a’ is called lower limit.
If f is an increasing or decreasing function on interval [a, b], then
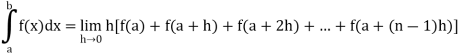
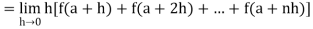
Where 
Properties-
1. The definite integral applies only if a<b, but it would be appropriate to include the case a = b and a>b as well, in that case-
If a = b, then
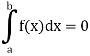
And if a>b, then
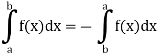
2. Integral of a constant function-
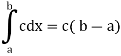
3. Constant multiple property-
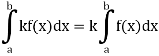
4. Interval union property-
If a < c < b, then
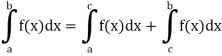
5. Inequality-
If c and d are constants such that 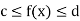 for all x in [a, b], then
for all x in [a, b], then
c (b – a)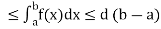
Note- if a function f: [a,b] →R is continuous, then the function ‘f’ is always Integrable.
Example-1: Evaluate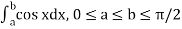 .
.
Sol. Here we notice that f:x→cos x is a decreasing function on [a, b],
Therefore, by the definition of the definite integrals-
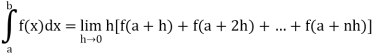
Then
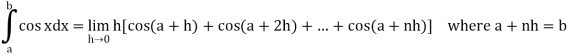
Now,
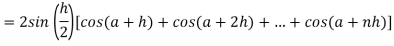

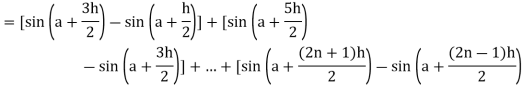
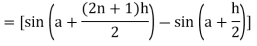
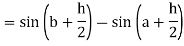
Here 
Thus
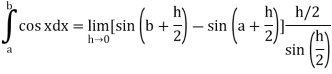
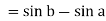
Example-2: Evaluate 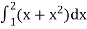
Sol. Here 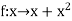 is an increasing function on [1, 2]
is an increasing function on [1, 2]
So that,
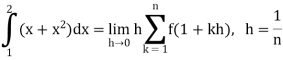
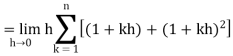
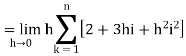
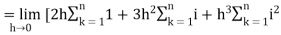 …. (1)
…. (1)
We know that-
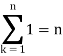
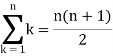
And 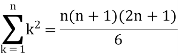
Then equation (1) becomes-

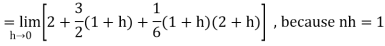
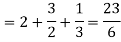
Note- we can find the definite integral directly as-

Example-3: Evaluate-
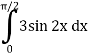
Sol. 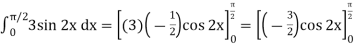
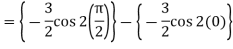
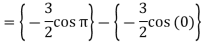
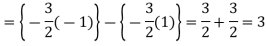
Improper integrals
(1) Let f is function defined on [a,∞) and it is integrable on [a, t] for all t >a, then
If 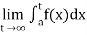 exists, then we define the improper integral of f over [a,∞) as follows-
exists, then we define the improper integral of f over [a,∞) as follows-
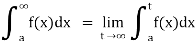
(2) Let f is function defined on (-∞,b] and it is integrable on [t, b] for all t >b, then
If 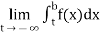 exists, then we define the improper integral of f over (-∞, b] as follows-
exists, then we define the improper integral of f over (-∞, b] as follows-
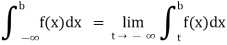
(3)Let f is function defined on (-∞, ∞] and it is integrable on [a, b] for every closed and bounded interval [a, b] which is the subset of R., then
If 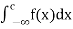 and
and 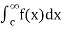 exist for some c belongs to R, then we define the improper integral of f over (-∞,∞) as follows-
exist for some c belongs to R, then we define the improper integral of f over (-∞,∞) as follows-
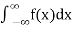 =
= 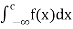 +
+ 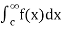
(4) Let f is function defined on (a,∞) and 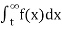 exists for all t>a, then
exists for all t>a, then
If 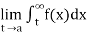 exists, then we define the improper integral of f over (a, ∞) as follows-
exists, then we define the improper integral of f over (a, ∞) as follows-
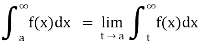
(5) Let f is function defined on (-∞, b) and 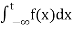 exists for all t<b, then
exists for all t<b, then
If 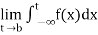 exists, then we define the improper integral of f over (-∞, b) as follows-
exists, then we define the improper integral of f over (-∞, b) as follows-
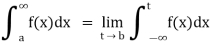
Improper integrals over finite intervals-
(1) Let f is function defined on (a, b] and 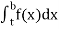 exists for all t ∈ (a,b), then
exists for all t ∈ (a,b), then
If 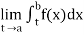 exists, then we define the improper integral of f over (a, b] as follows-
exists, then we define the improper integral of f over (a, b] as follows-
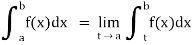
(2) Let f is function defined on [a, b) and 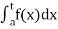 exists for all t ∈ (a,b), then
exists for all t ∈ (a,b), then
If 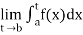 exists, then we define the improper integral of f over [a, b) as follows-
exists, then we define the improper integral of f over [a, b) as follows-
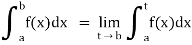
(3) Let f is function defined on [a, c) and (c, b]. If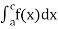 and
and 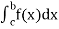 exist
exist
Then we define the improper integral of f over [a, b] as follows-
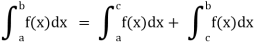
The beta and gamma functions are defined as-
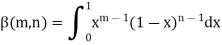
And
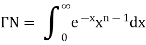
These integrals are also known as first and second Eulerian integrals.
Note- Beta function is symmetrical with respect to m and n.
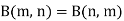
Some important results-
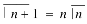
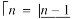
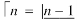
Ex.1: Evaluate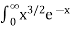 dx
dx
Solution dx =
dx = 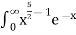 dx
dx
= Γ (5/2)
= Γ (3/2+ 1)
= 3/2 Γ (3/2)
= 3/2. ½ Γ (½)
= 3/2. ½ π
= ¾ π
Ex. 2: Find γ(-½)
Solution: (-½) + 1= ½
Γ (-1/2) =Γ (-½ + 1) / (-½)
= - 2 Γ (1/2)
= - 2 π
Ex. 3: Show that 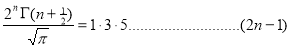

Solution:
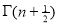 =
= 
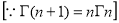
= 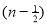
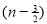
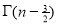
= 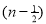
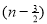
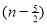
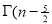 ) .......................
) .......................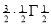
= 
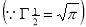
= 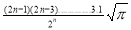
Ex. 4: Evaluate 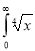
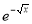 dx.
dx.
Solution: Let 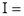
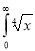
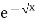 dx
dx
X | 0 | 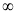 |
t | 0 | 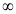 |
Put  or
or 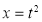 ;dx =2t dt
;dx =2t dt
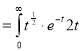 dt
dt
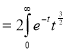 dt
dt
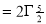
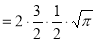
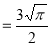
Ex. 5: Evaluate 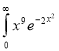 dx.
dx.
Solution: Let 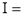
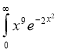 dx.
dx.
x | 0 |  |
t | 0 |  |
Put 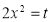 or
or  ; 4x dx = dt
; 4x dx = dt
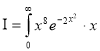 dx
dx
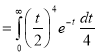
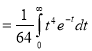
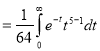
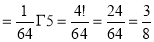
Evaluation of beta function 𝛃 (m, n)-
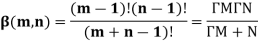
Here we have-
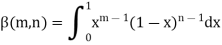
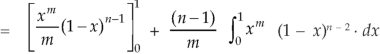
Or
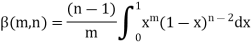
Again, integrate by parts, we get-
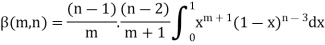
Repeating the process above, integrating by parts we get-

Or
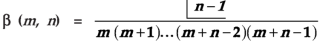
Evaluation of gamma function-
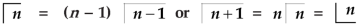
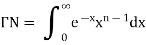
Integrating by parts, we take 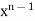 as first function-
as first function-
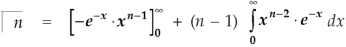

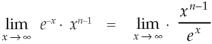
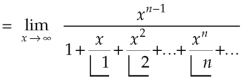
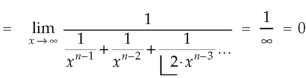
We get-
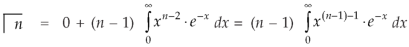
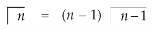
Replace n by n+1,
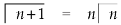
Relation between beta and gamma function-
We know that-

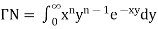 ………… (1)
………… (1)
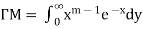 …………………..(2)
…………………..(2)
Multiply equation (1) by 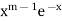 , we get-
, we get-

Integrate both sides with respect to x within limits x = 0 to x =  , we get-
, we get-
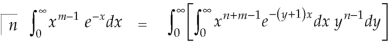
But
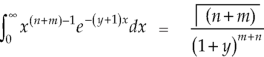
By putting λ= 1 + y and n = m + n
We get by using this result in (2)-

So that-
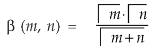
Definition: Beta function

Properties of Beta function:
Example (1): Evaluate I = 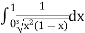
Solution:
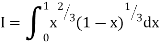
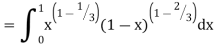

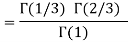
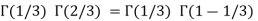

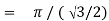
= 2 π/3
Example (2): Evaluate: I = 02 x2 / (2 – x). Dx
Solution:
Letting x = 2y, we get
I = (8/2) 01 y2 (1 – y)-1/2dy
= (8/2). B (3, 1/2)= 642 /15
Beta Function More Problems
Relation between Beta and Gamma functions:
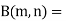

Example(1): Evaluate: I = 0a x4 (a2 – x2). Dx
Solution: Letting x2 = a2y, we get
I = (a6 / 2) 01 y3/2 (1 – y )1/2dy
= (a6 / 2).B (5/2, 3/2)
= a6 /3 2
Example (2): Evaluate: I = 02 x (8 – x3). Dx
Solution: Let x3 = 8y
I = (8/3) 01 y-1/3 (1 – y) 1/3. Dy
= (8/3) B (2/3, 4/3)
= 16 π / (93)
Example(3): Prove that
Solution: Let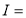
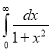
Put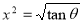 or
or 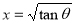 ,
, 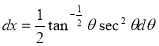
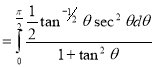
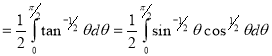
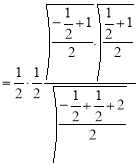
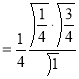
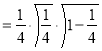


Example(4): Evaluate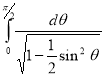
Solution: Let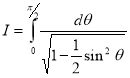
Put 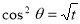 or
or  ,
,
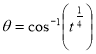 ,
,
When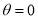 ,
,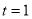 ;
;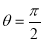 ,
,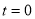
Also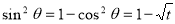
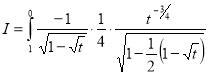

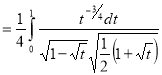
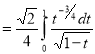
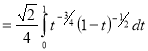
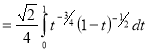
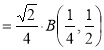
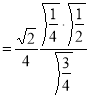
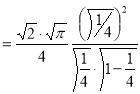
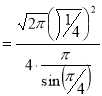
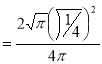
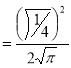
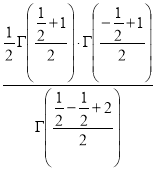
Example(5): Show that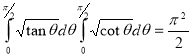
Solution: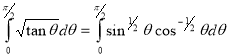
=
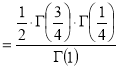
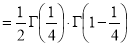
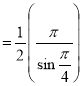
 (
(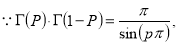 0<p<1)
0<p<1)
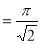
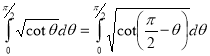
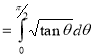
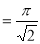 (By above result)
(By above result) 
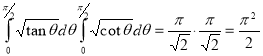
RULE I: If 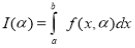 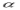 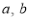 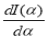 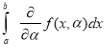 |
Q1) Evaluate: (i) 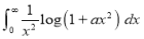
Sol) Let  Differentiating by DUIS rule 
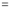 
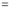 
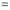 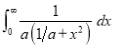
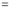 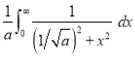
 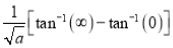
  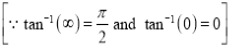 Separating vectors and integrating, we have
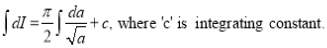  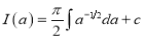  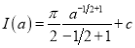  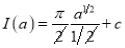  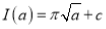 Putting 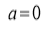 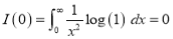  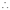 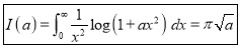
(ii) 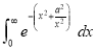 Solution: Let 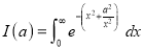 Differentiating by DUIS rule 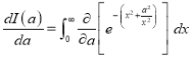
 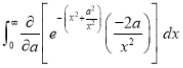
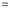 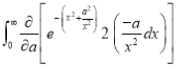 Put 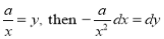  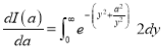
 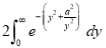
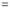 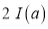 Integrating, we get
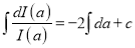
 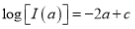 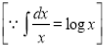
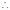 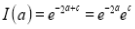
 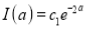 Putting 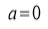 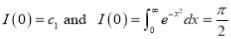 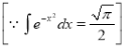  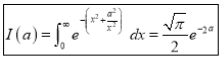
|
DIFFERENTIATION UNDER INTEGRAL SIGN RULE – II
(Leibnitz’s Rule)
RULE II: If 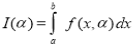    
|
Q)Prove that: (i) If 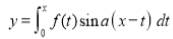 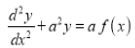
Sol) We have given that
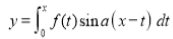 Then we have to prove that 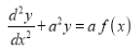 Differentiating by DUIS rule (Leibnitz’s Rule), we have 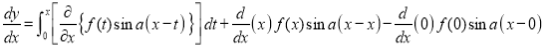
 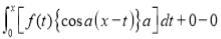
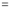 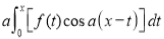 Again differentiating by DUIS rule (Leibnitz’s Rule), we have 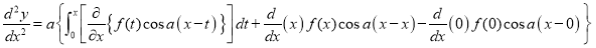 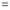 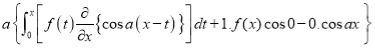
 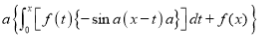
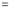 
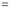 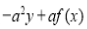   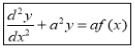 This is the desired result.
(ii)If 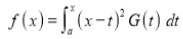 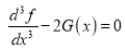 Solution: We have given that
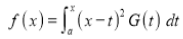 Then we have to prove that 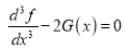 Differentiating by DUIS rule (Leibnitz’s Rule), we have 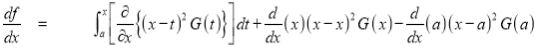 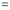   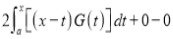 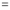 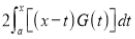 Again differentiating by DUIS rule (Leibnitz’s Rule), we have 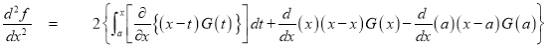
 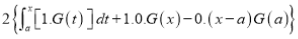
 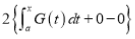
 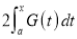 Again differentiating by DUIS rule (Leibnitz’s Rule), we have 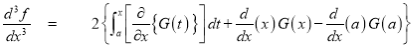
 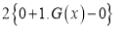
 
 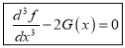
|
ERROR FUNCTION
Introduction to error function and its properties.
Error Function:
- Error function is denoted by
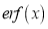 and defined as
and defined as
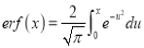
2. Complementary Error function is denoted by 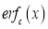 and defined as
and defined as
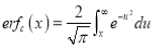
3. Properties of Error function
(i) 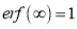
(ii) 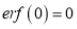
(iii) 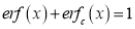
(iv) 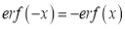 i.e. error function is odd function.
i.e. error function is odd function.
(v) 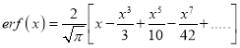
Q) Prove that
(i) 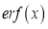 is an odd function and hence deduce
is an odd function and hence deduce 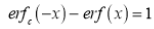 .
.
Sol)
We have to prove that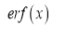 is an odd function i.e.
is an odd function i.e.
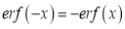
We know that
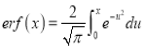 - - - - - - - - - - - - - - - - (1)
- - - - - - - - - - - - - - - - (1)
Replace 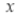 by
by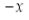 , we have
, we have
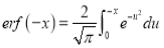
Put 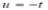 , then
, then  and
and

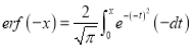
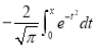
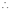

Hence the error function is odd function.
Now we have to prove that
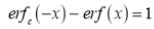
Consider
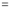
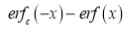
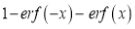
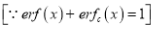
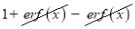
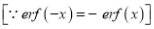

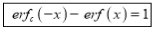
This is the desired result.
(ii)
 .
.
Solution:
We have to prove that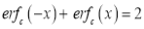
Consider

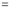
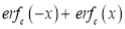
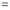
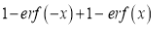
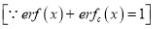


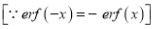

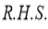

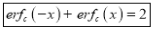
This is the desired result.
(iii) 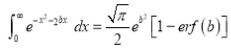
Solution:
We have to prove that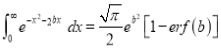
Consider
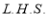
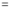
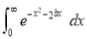

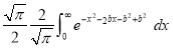
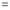
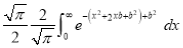
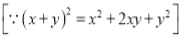
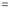
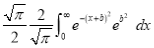
Put 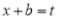 , then
, then 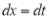 and
and
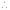
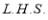
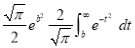
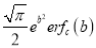
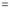
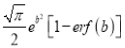
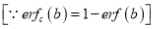
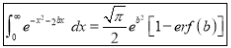
This is the desired result.
(iv) 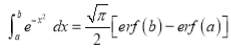
Solution:
We have to prove that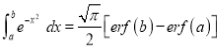
We know that

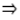
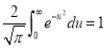

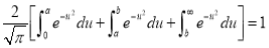

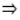
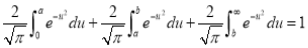

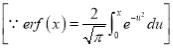




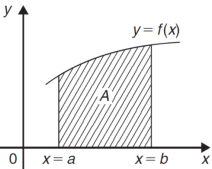
Area in Cartesian coordinates-
Example-1: Find the area enclosed by two curves using double integration.
y = 2 – x and y² = 2 (2 – x)
Sol. Let,
y = 2 – x ………………..(1)
And y² = 2 (2 – x) ………………..(2)
On solving eq. (1) and (2)
We get the intersection points (2,0) and (0,2) ,
We know that,
Area = 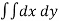
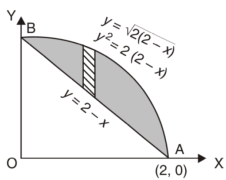
Here we will find the area as below,
Area = 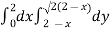
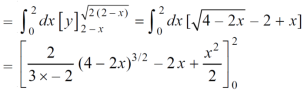
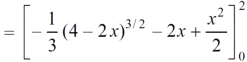
Which gives,
= ( - 4 + 4 /2 ) + 8 / 3 = 2 / 3.
Example-2: Find the area between the parabola y ² = 4ax and another parabola x² = 4ay.
Sol. Let,
y² = 4ax ………………..(1)
And
x² = 4ay…………………..(2)
Then if we solve these equations , we get the values of points where these two curves intersect
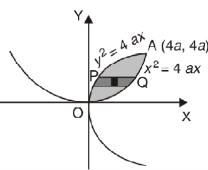
x varies from y²/4a to  and y varies from o to 4a,
and y varies from o to 4a,
Now using the conceot of double integral,
Area = 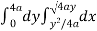
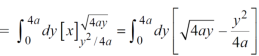
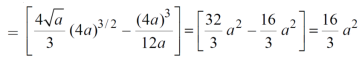
Area in polar coordinates-
Example-3: Find the area lying inside the cardioid r = a(1+cosθ) and outside the circle r = a, by using double integration.
Sol. We have,
r = a(1+cosθ) …………………….(1)
And
r = a ……………………………….(2)
On solving these equations by eliminating r , we get
a(1+cosθ) = a
(1+cosθ) = 1
Cosθ = 0
Here a θ varies from – π/2 to π/2
Limit of r will be a and 1+cosθ)
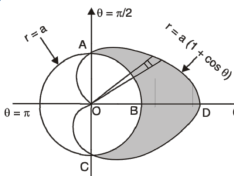
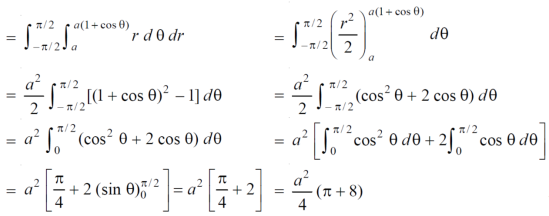
Which is the required area.
Example-4: Find the are lying inside a cardioid r = 1 + cosθ and ouside the parabola r(1 + cosθ) = 1.
Sol. Let,
r = 1 + cosθ ……………………..(1)
r(1 + cosθ) = 1……………………..(2)
Solving these equestions , we get
(1 + cosθ )(1 + cosθ ) = 1
(1 + cosθ )² = 1
1 + cosθ = 1
Cosθ = 0
θ = ±π / 2
So that, limits of r are,
1 + cosθ and 1 / 1 + cosθ
The area can be founded as below,
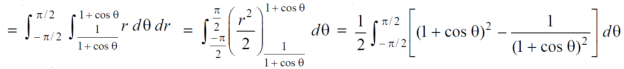

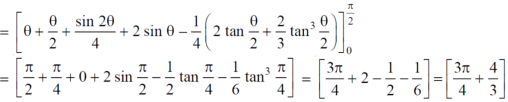
Double integrals as volumes
Suppose we have a curve y = f(x) is revolved about an axis , then a solid is generated , now we need to find out the volume of the solid generated ,
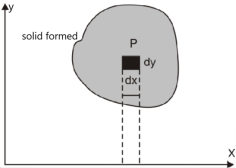
The formula for volume of the solid generated about x-axis,
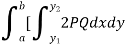
Example-1: Calculate the volume generated by the revolution of a cardioid,
r = a ( 1 – cosθ) about its axis
Sol. Here, r = a ( 1 – cosθ)
Volume =
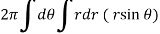
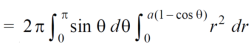
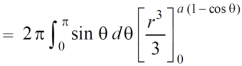
=
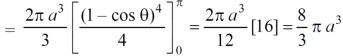
Which is the volume of generated by cardioid.
Example-2: Find the volume generated by revolving a circle x ² + y² = 4 about the line x= 3.
Sol. We know that,
Volume = 
Here , PQ = 3 – x,
= 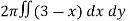

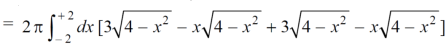
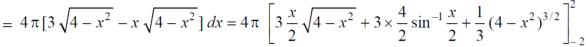
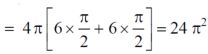
The volume is 24π².
Example-3: Calculate the volume under the surface z = 3 + x² - 2y over the region R defined as 0≤ x ≤ 1 and -x ≤ y ≤ x
Sol. The is a double integral of z = 3 + x² - 2y over the region R .
Volume will be,
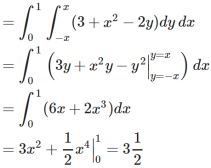
Areas and volumes of revolutions
The volume of revolution (V) is obtained by rotating area A through one revolution about the x-axis is given by-
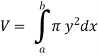
Suppose the curve x = f(y) is rotated  about y-axis between the limits y = c and y = d, then the volume generated V, is given by-
about y-axis between the limits y = c and y = d, then the volume generated V, is given by-
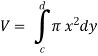
Example-1: Find the area enclosed by the curves 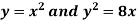 and if the area is rotated
and if the area is rotated  about the x-axis then determine the volume of the solid of revolution.
about the x-axis then determine the volume of the solid of revolution.
Sol. We know that, at the point of intersection the coordinates of the curve are equal. So that first we will find the point of intersection-
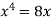
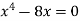
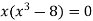
We get,
x = 0 and x = 2
The curve of the given equations will look like as follows-
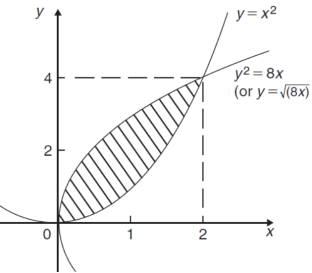
Then,
The area of the shaded region will be-
A = 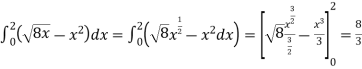
So that the area will be 8/3 square unit.
The volume will be
= (volume produced by revolving 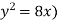 – (volume produced by revolving
– (volume produced by revolving 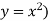
= 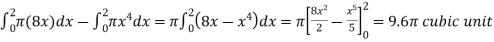
Method of cylindrical shells-
Let f(x) be a continuous and positive function. Define R as the region bounded above by the graph f(x), below by the x-axis, on the left by the line x = a and on the right x = b, then the volume of the solid of revolution formed by revolving R around the y-axis is given by

Example-2: Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 1/x over the interval [1 , 3].
Sol. The graph of the function f(x) = 1/x will look like-
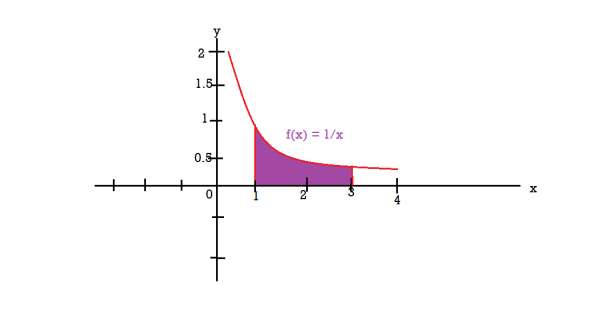
The volume of the solid of revolution generated by revolving R(violet region) about the y-axis over the interval [1 , 3]
Then the volume of the solid will be-
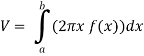
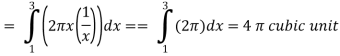
Example-3: Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 2x - x² over the interval [0 , 2].
Sol. The graph of the function f(x) = 2x - x² will be-
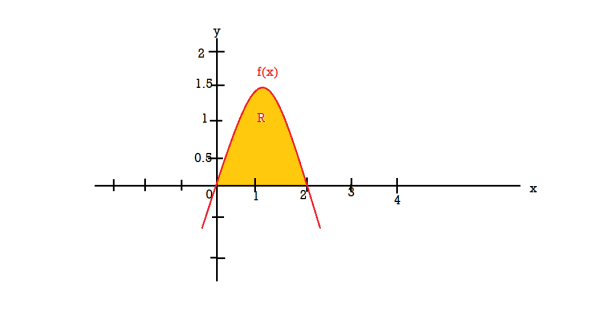
The volume of the solid is given by-
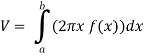
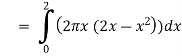
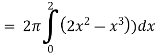
= 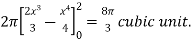
Area of surfaces of revolution
Suppose we have a curve y = f(x) and if we revolve this curve around x – axis then the area formed is known as surface area of revolution.
Let f(x) be a non-negative smooth function over the interval[ [ a , b] , then the surface area of the surface of revolution formed by revolving the graph of f(x) around x-axis is given by,
S = 
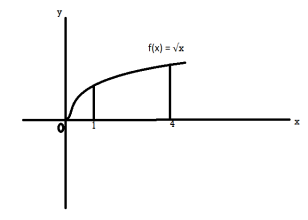
Example-1: Find the surface of the surface generated by revolving the graph f(x) = 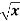 over the interval [1,4] around x-axis.
over the interval [1,4] around x-axis.
Sol. The graph of the function will look like
f(x) = 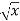 then f’(x) = 1/2 (
then f’(x) = 1/2 (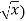
(f’(x))² = 1/4x
Then,
S = 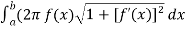
S = 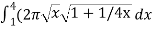
S = 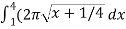 ,
,
Let u = 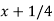 , then du = dx, when x = 1 , u = 5/4 and when x = 4 , u = 17/4,
, then du = dx, when x = 1 , u = 5/4 and when x = 4 , u = 17/4,
This will give,
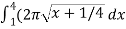 =
= 
On solving the integral we get,
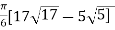 = 30.84 (approx.)
= 30.84 (approx.)
Example-1: find the surface of the surface generated by revolving the graph g(y) = 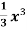 over the interval [0,2] around y-axis.
over the interval [0,2] around y-axis.
Sol.
Hint - use formula
S = 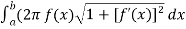
Ans. = 24.118
CENTER OF MASS AND GRAVITY-
Centre of mass-
We have-
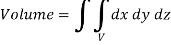
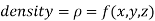
Mass = volume 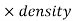

Example: Find the mass of a plate formed by the coordinate planes and the plane-
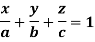
The variable density 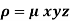
Sol.
Here we the mass will be-
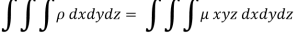
The limits of y are from y = 0 to y = b(1 – x/a) and limits of x are from 0 to a.
Therefore the required mass will be-
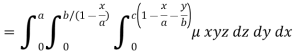
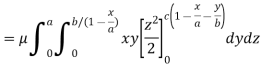
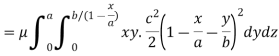
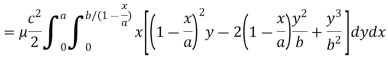
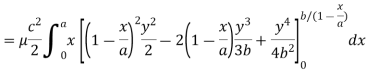
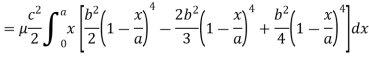

Which is the required answer.
Centre of gravity-
The centre of gravity of a lamina is the point where it balances perfectly which means the lamina’s centre of mass.
If  and
and 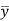 are the coordinates of the centroid C of area A, then-
are the coordinates of the centroid C of area A, then-
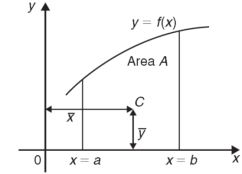
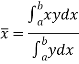
And
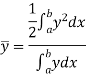
Example: Determine the coordinates of the centroid of the area lying between the curve y = 5x - x² and the x-axis.
Sol.
Here y = 5x - x²when y = 0, x = 0 or x = 5
Therefore the curve cuts the x-axis at 0 and 5 as in the figure-
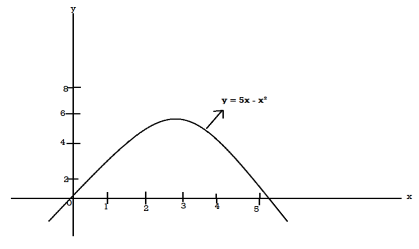
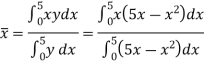
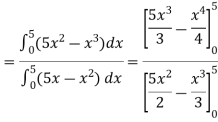
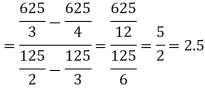
Now
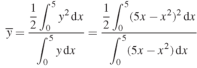



= 2.5
Therefore the centroid of the area lies at (2.5, 2.5)
Key takeaways-
- The formula for volume of the solid generated about x-axis,

2. Centre of mass-
We have-
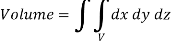
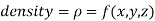
Mass = volume 
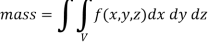
References:
1. G.B. Thomas and R.L. Finney, “Calculus and Analytic Geometry”, Pearson, 2002.
2. T. Veerarajan, “Engineering Mathematics”, McGraw-Hill, New Delhi, 2008.
3. B. V. Ramana, “Higher Engineering Mathematics”, McGraw Hill, New Delhi, 2010.
4. N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
5. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
6. HK Dass