Unit - 3
Static Forces on Surface and Buoyancy
Fluid statics is concerned with the issues that arise when fluids are at rest. It doesn't matter if the fluid is gaseous or liquid. When the fluid is a liquid, it is referred to as hydrostatics, and when the fluid is a gas, it is referred to as aerostatics. There is no relative motion between adjacent fluid layers in fluid statics, hence there are no shear (tangential) forces in the fluid that are attempting to distort it. In fluid statics, the only stress we deal with is the usual stress, which is pressure, and pressure variation is caused only by the fluid's weight.
Because there is no relative motion between the fluid and the solid surface, the force applied on the surface by a fluid at rest is normal to the surface at the point of contact. As a result, no shear forces can act parallel to the surface.
The forces acting on floating or submerged bodies, as well as the forces generated by hydraulic presses and automobile jacks, are determined using fluid statics. Many engineering systems, such as water dams and liquid storage tanks, need the use of fluid statics to determine the forces acting on the surfaces. The magnitude, direction, and line of action of the resultant hydrostatic force acting on a submerged surface must all be determined before the force can be fully described.
When a surface is submerged in a fluid, the fluid exerts forces on the surface. These forces must be determined for designing storage tanks, ships, dams, and other hydraulic structures. Because there are no shearing stresses in a fluid at rest, the force must be perpendicular to the surface.
We also know that the pressure will vary linearly with depth if the fluid is incompressible.
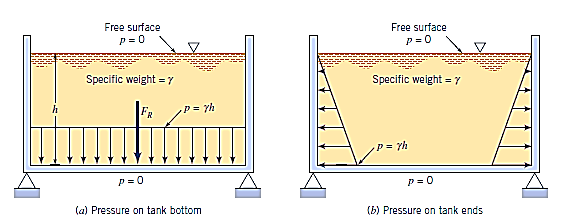
The magnitude of the resultant force for a horizontal surface, such as the bottom of a liquid-filled tank, is simply
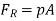
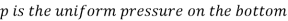
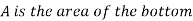
For the open tank
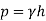
The resultant force on the bottom is solely attributable to the liquid in the tank if atmospheric pressure operates on both sides of the bottom, as shown. The resultant force acts through the centroid of the area, as illustrated, because the pressure is constant and uniformly distributed over the bottom. For the open tank the pressure on the ends of the tank is not uniformly distributed.
The determination of the resultant force acting on the surface is more involved in the more general example of a submerged plane surface that is inclined. We'll pretend that the fluid surface is exposed to the atmosphere for the time being. Allow the plane in which the surface is located to intersect the free surface at 0 degrees and form an angle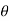 
with it.
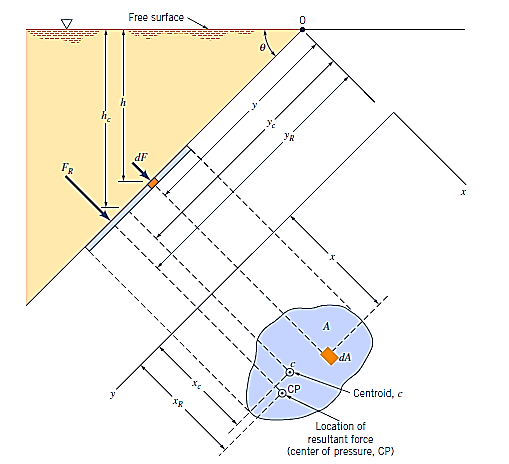
As indicated, the x–y coordinate system is defined with 0 as the origin and y= 0 (i.e., the x axis) directed along the surface. The shape of the region can be whatever you want it to be, as illustrated. The direction, position, and magnitude of the resultant force acting on one side of this region due to the liquid in contact with the area are all things we want to know.
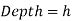
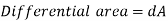
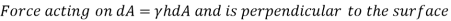
Summing these differential forces over the entire surface yields the amount of the resultant force. In formula form
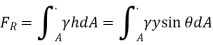
Were,
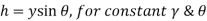
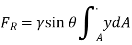
We can express the integral appearing as the initial moment of the area with respect to the x axis.
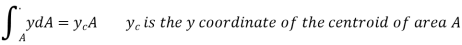
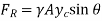
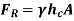
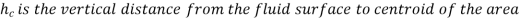
The magnitude of the force is independent of the angle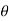 
.
It is solely determined by the fluid's specific weight, total area, and the depth of the centroid of the area below the surface.
Although our intuition could lead us to believe that the resultant force should pass through the area's centroid, this is not the case.
Summation of moments around the x axis can be used to estimate the y coordinate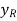 
of the resultant force. That is, the resultant force's moment must be equal to the distributed pressure force's moment.
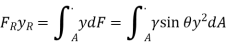
Therefore,
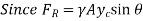
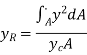
The second moment of the area (moment of inertia)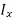 
is the integral in the numerator, with respect to an axis defined by the intersection of the plane containing the surface and the free surface (x axis).
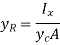
Use can now be made of the parallel axis theorem to express
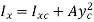
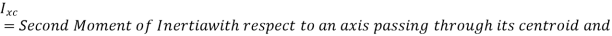
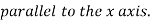
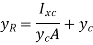
The resultant force does not pass through the centroid but for nonhorizontal surfaces is always below since,
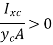
Similarly for x coordinate,
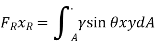
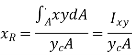
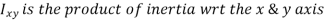
Using parallel axis theorem
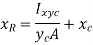
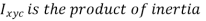
With respect to an orthogonal coordinate system established by a translation of the x–y coordinate system and passing through the centroid of the area. The resulting force must lie along the line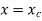 
if the submerged area is symmetrical with respect to an axis passing through the centroid and parallel to either the x or y axis, since
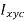is identically zero in this case. The centre of pressure is the place through which the resultant force acts.
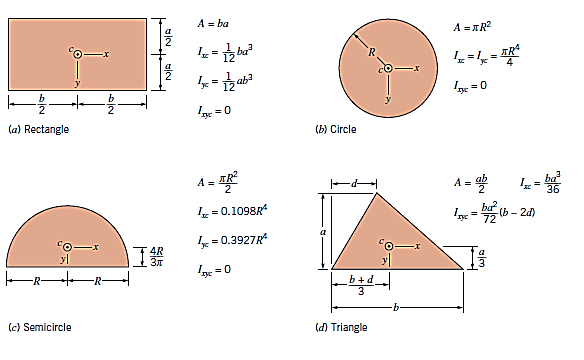
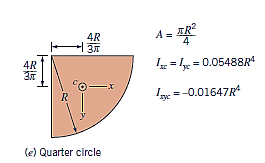
Key Takeaway:
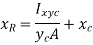
Vertical Plane Surface:
Consider a thin horizontal strip of the surface of thickness dx and breadth b.
Let the depth of the strip be x.
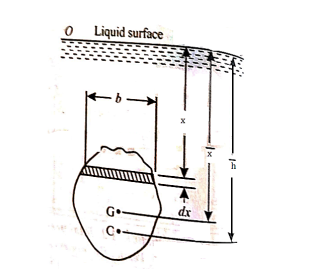
Let the intensity of pressure on strip be p.
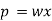
Total pressure on the strip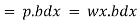 
Total pressure on the whole area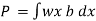 
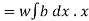
But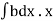 
= Moment of the surface area about the liquid level = A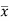
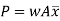
Moment of the pressure about free surface
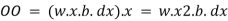
Total Moment,
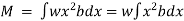
But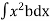 
= Moment of inertia of the surface about free surface OO (I0)
Hence, M = wI0
The sum of the moment of the pressure is also equal to P×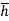
.
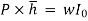
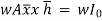
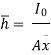
But
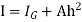
Above equation becomes
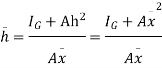
Inclined plane surface:
Let A = area of the surface
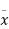= depth of the centre of gravity from the free liquid surface.
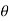=angle at which the immersed surface is inclined with the liquid surface.
w=specific weight of liquid.
Consider a strip of thickness dx width b at a distance l from O.
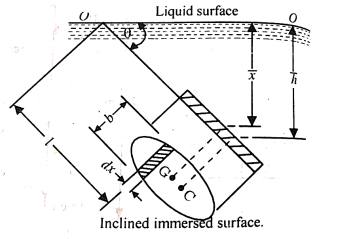
The intensity of pressure on the strip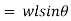 
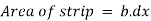
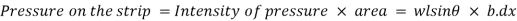
Total pressure on the surface
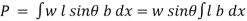
But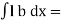 
Moment of surface about OO
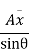
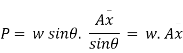
Let,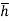 
= Depth of centre of pressure below free liquid surface
IG = Moment of inertia of the immersed surface about 00.
Moment of pressure about OO
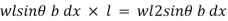
Sum of moments about O
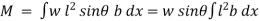
But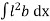 
= I0 = Moment of inertia of the surface about point O
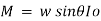
Sum of moment of all such pressure about O is also equal to
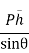
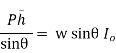
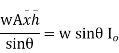
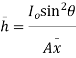
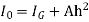
Were,
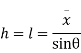
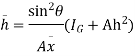
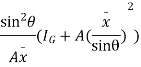
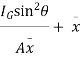
Key Takeaway:
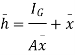
Pressure Prism:
The force created by a fluid operating on a planar rectangular region can be represented graphically in a way that is both informative and practical. Consider the pressure distribution along a vertical wall of a tank with a fixed width b and a given specific weight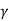 
of liquid.
Since the pressure must vary linearly with depth we can represent the variation as
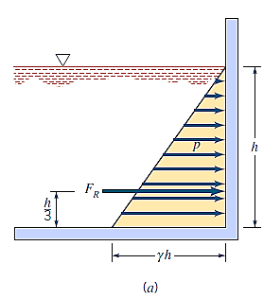
Where the pressure is equal to zero at the upper surface and equal to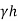 
at the bottom.
The resultant force acting on the rectangular area,
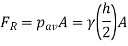
The three-dimensional representation of the pressure distribution can be drawn as follows
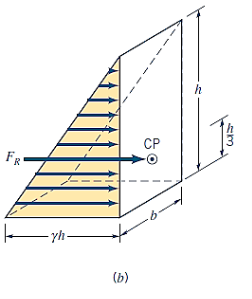
The flat surface of interest is the base of this "volume" in pressure-area space, and its altitude at each point is the pressure. The pressure prism is the volume of the resultant force operating on the rectangular surface, and it is obvious that the magnitude of the resultant force acting on the rectangle surface is equal to the volume of the pressure prism.
The Fluid force is,
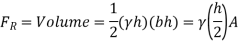
The resulting force must pass through the pressure prism's centroid. The centroid of the volume under examination is placed along the surface's vertical axis of symmetry and at a distance 
above the base (since the centroid of a triangle is located at 
above its base).
Same graphical approach can be used for plane rectangular surfaces that do not extend up to the fluid surface,
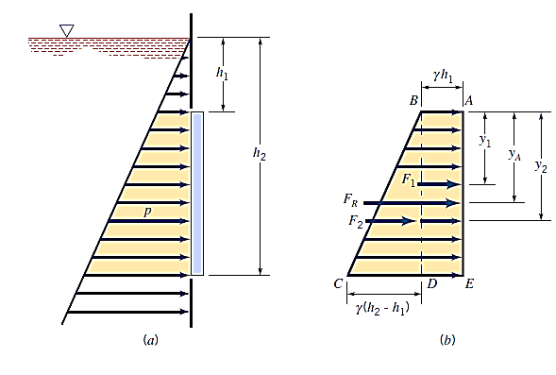
The pressure prism's cross section is trapezoidal in this case. The resultant force, however, is still equal in magnitude to the pressure prism's volume, and it flows via the volume's centroid. Decomposing the pressure prism into two pieces, ABDE and BCD, as indicated, yields certain values.
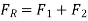
The components can be easily identified by looking for rectangular surfaces. Summing moments along a convenient axis, such as one passing through A, can be used to find the location of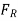 
. In this situation,
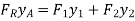
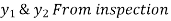
The pressure prism can still be formed for inclined plane rectangular surfaces, and the cross section of the prism will be trapezoidal in most cases.
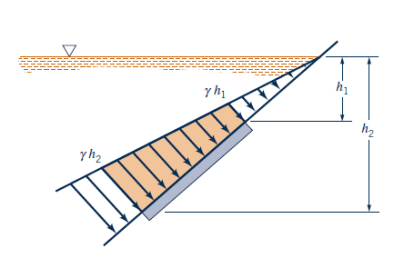
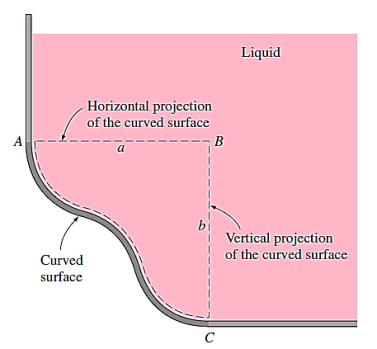
The computation of the resultant hydrostatic force for a submerged curved surface is more complicated because it often includes the integration of pressure forces that change direction along the curved surface. Because of the intricate shapes involved, the pressure prism notion isn't much use in this scenario.
The horizontal and vertical components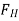 
and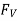 
must be determined individually to obtain the resultant hydrostatic force 
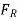acting on a two-dimensional curved surface. The free body diagram of the liquid block surrounded by the curved surface and the two plane surfaces (one horizontal and one vertical) going through the two ends of the curved surface are used to accomplish this.
The horizontal surface of the liquid block is simply the projection of the curved surface on a horizontal plane, and the vertical surface is simply the projection of the curved surface on a vertical plane.
Newton's third law states that the force acting on the curved solid surface is equal to and opposite to the force acting on the curved liquid surface.
It is possible to determine the force operating on the imaginary horizontal or vertical plane surface, as well as its path of action.
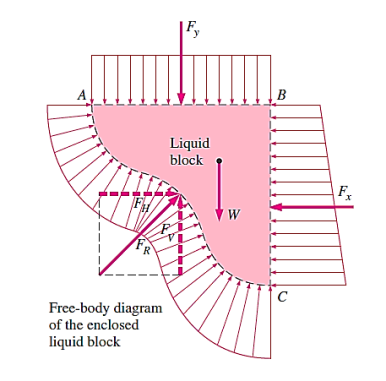
The weight of the enclosed liquid block of volume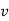 
is,
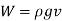
It acts downward through the centroid of this volume. Noting that the fluid block is in static equilibrium, the force balances in the horizontal and vertical directions give,
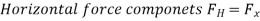
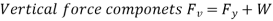
- The horizontal component of the hydrostatic force acting on a curved surface is equal to the hydrostatic force acting on the curved surface's vertical projection (in magnitude and line of action).
- The vertical component of the hydrostatic force acting on a curved surface equals the hydrostatic force acting on the curved surface's horizontal projection plus (or minus, if acting in the opposite direction) the weight of the fluid block.
The magnitude of the resultant hydrostatic force acting on the curved surface is
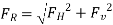
The tangent of the angle it makes with the horizontal is
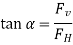
By taking a moment around an appropriate point, the exact location of the resultant force's line of action (e.g., its distance from one of the curved surface's end points) can be calculated. These considerations apply to all curved surfaces, whether they are above or below the liquid. Because they act in different directions, the weight of the liquid is removed from the vertical component of the hydrostatic force when a curved surface is above a liquid.
The resultant hydrostatic force acting on the surface always flows through the centre of the circle when the curved surface is a circular arc (whole circle or any part of it). This is due to the fact that pressure forces are normal to the surface, and all lines normal to a circle's surface pass through its centre. As a result, at the centre, the pressure forces form a concurrent force system that may be reduced to a single equivalent force.
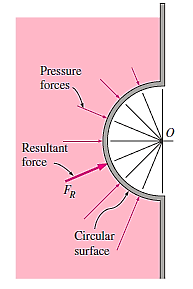
Finally, hydrostatic forces acting on a plane or curved surface submerged in a multi-layered fluid of varying densities can be calculated by treating different parts of surfaces in different fluids as separate surfaces, calculating the force on each part, and then adding the forces using vector addition. It can be represented as for a planar surface as
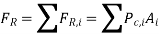
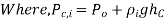
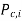is the pressure in fluid I at the centroid of the section of the surface, and 
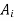is the area of the plate in that fluid. The constraint that the moment of the equivalent force about any point equals the total of the moments of the individual forces about the same point can be used to establish the equivalent force's course of action.
Key Takeaway:
It's a frequent observation that an object in a liquid seems lighter and weighs less than it does in air. This can be easily shown by using a waterproof spring scale to weigh a heavy object in water. Floating on water are also things made of wood or other light materials. These and other findings indicate that a fluid exerts an upward force on a body submerged in it. The buoyant force, indicated by the letter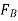 
, is a force that tends to lift the body.
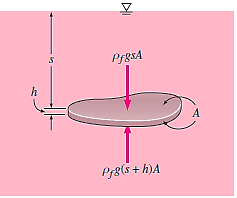
The area of the top (and bottom) surface of the plate is A, and its distance to the free surface is s.
The pressures at the top and bottom surfaces of the plate are,
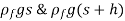
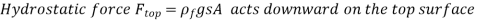
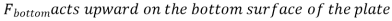
The difference between these two forces is a net upward force, which is the buoyant force,
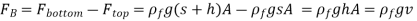
The weight of the liquid displaced by the plate equals the buoyant force exerted on it. It's worth noting that the buoyant force is independent of the body's distance from the free surface. It is also unaffected by the solid body's density.
The relationship was created for a simple geometry, but it applies to any body, regardless of shape. This can be demonstrated mathematically using a force balance, or simply by using the following logic: Consider a randomly shaped solid body submerged in a fluid at rest and contrast it with a fluid body of the same shape depicted by dotted lines at the same distance from the free surface.
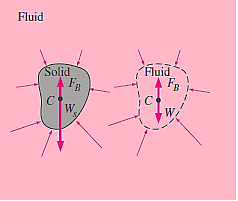
The buoyant forces acting on these two entities are the same because the pressure distributions at their boundaries, which are only dependent on depth, are the same. The net force and net moment exerted on the imaginary fluid body are zero because it is in static equilibrium. As a result, the upward buoyant force must equal the weight of the imaginary fluid body whose volume equals the solid body's volume. To achieve a zero moment, the weight and the buoyant force must have the same line of action. This is known as Archimedes’ principle.
“The buoyant force acting on a body immersed in a fluid is equal to the weight of the fluid displaced by the body, and it acts upward through the centroid of the displaced volume.”
Key Takeaway:
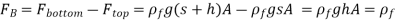
The weight of the entire body must be equal to the buoyant force, which is the weight of the fluid whose volume is equal to the volume of the floating body's submerged component.
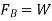
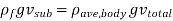
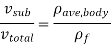
As a result, the submerged volume percentage of a floating body equals the ratio of the body's average density to the fluid's density. The floating body becomes entirely immersed when the density ratio is equal to or greater than one.
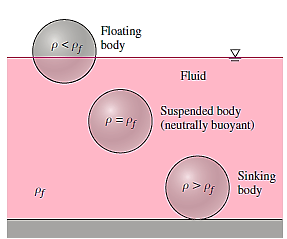
It follows from these discussions that a body immersed in a fluid
- Remains at rest at any point in the fluid when its density is equal to the density of the fluid.
- Sinks to the bottom when its density is greater than the density of
- The fluid.
- Rises to the surface of the fluid and floats when the density
- Of the body is less than the density of the fluid.
Because the buoyant force is related to the fluid's density, one might assume that the buoyant force exerted by gases like air is insignificant. This is true in general, but there are a few notable outliers.
The rise of warm air in a cooler environment, and hence the onset of natural convection currents, the rise of hot-air or helium balloons, and air motions in the atmosphere are all dominated by the buoyancy effects in gases. A helium balloon, for example, will rise due to the buoyancy effect until it reaches an altitude where the density of air (which drops with altitude) matches the density of helium in the balloon—assuming the balloon does not burst before then and the weight of the balloon's skin is ignored.
In modern geology, Archimedes' concept is applied by considering the continents to be floating on a sea of magma.
Key Takeaway:
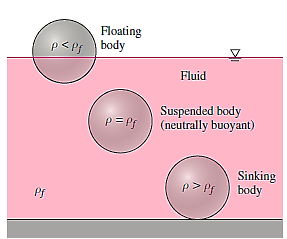
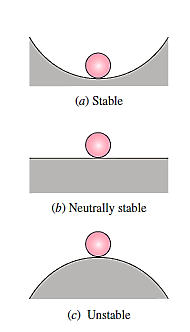
Three balls resting on the floor are shown in Figure. Case (a) is stable because any minor disturbance (moving the ball to the right or left) causes a restoring force (due to gravity) to return it to its original location. Case (b) is neutrally stable because the ball will stay put in its new place if it is moved to the right or left. It has no inclination to return to its original site or to go further.
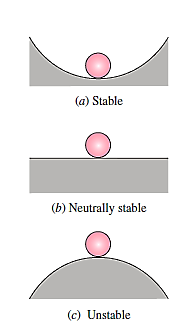
Case (c) is a circumstance in which the ball is at rest at the time, but any disturbance, no matter how minor, causes it to roll off the hill—it does not return to its original position, but rather diverges from it. This scenario is precarious.
The weight and buoyant force acting on an immersed or floating body in static equilibrium balance each other, and such bodies are intrinsically stable in the vertical direction. If a neutrally buoyant body is immersed and then elevated or lowered to a different depth, the body will remain in equilibrium at that depth. If a vertical force raises or lowers a floating body, the body will return to its original position as soon as the external effect is removed. As a result, a floating body has vertical stability, whereas a neutrally buoyant body immersed in water has neutral stability because it does not return to its former position after a disturbance.
Key Takeaway:
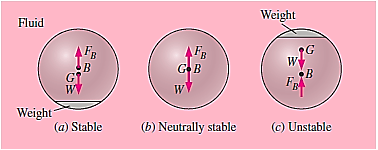
The relative locations of the body's centre of gravity G and the centre of buoyancy B, which is the centroid of the displaced volume, determine the rotational stability of an immersed body. If the body is bottom-heavy, and thus point G is directly below point B, an immersed body is stable. In such instances, a rotational disruption of the body causes a restoring moment, which allows the body to return to its original stable position. In order to move the weight to the bottom as much as possible, a stable submarine design demands for the engines and crew cabins to be situated in the lower half.
Because the cage that carries the load is at the bottom in hot-air or helium balloons (which can be considered as being immersed in air) are also stable. A submerged body with its centre of gravity G directly above point B is unstable, and any disturbance will force it to flip over. G and B must coincide for a body to be neutrally stable. This is true for bodies with a consistent density throughout. There is no inclination for such bodies to topple or right themselves.
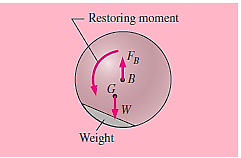
It cannot be at rest if the centre of gravity is not vertically aligned with the centre of buoyancy; it will spin toward its stable state even if no disturbance occurs.
In the figure above, the restoring moment is counter-clockwise, causing the body to rotate counter-clockwise, aligning point G vertically with point B. Although there may be some oscillation, the body eventually settles into a stable equilibrium state.
Key Takeaway:
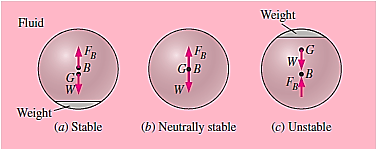
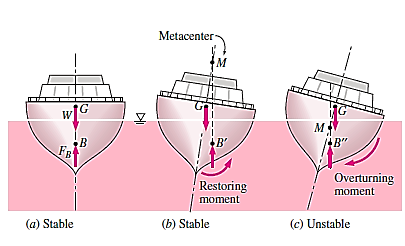
For floating bodies, the rotational stability conditions are similar. The body is always stable if the floating body is bottom-heavy and hence the centre of gravity G is directly below the centre of buoyancy B. A floating body, unlike immersed bodies, may be stable when G is exactly above B. This is because, during a rotational disturbance, the centroid of the displaced volume shifts to the side to a location 
, while the body's centre of gravity G remains intact.
These two forces form a restoring moment and return the body to its original position if point 
, is far enough away. The metacentric height GM, which is the distance between the centre of gravity G and the metacentre M—the junction locations of the lines of action of the buoyant force through the body before and after rotation—is a measure of floating body stability. For minor rolling degrees up to around 20°, the metacentre can be regarded a fixed position for most hull forms.
If point M is above point G, and thus GM is positive, a floating body is stable; if point M is below point G, and thus GM is negative, it is unstable. The weight and buoyant force acting on the tilted body produce an overturning moment rather than a restoring moment in the later situation, causing the body to capsize. The length of the metacentric height GM above G indicates the floating body's stability: the longer it is, the more stable it is.
Key Takeaway:
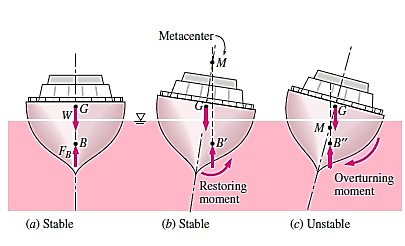
When a floating body is tilted by a slight degree, it begins to oscillate around the point where the body is slanted.
The point at which the line of action of the force of buoyancy meets the normal axis of the body when the body is given a modest rotational displacement is also known as the meta-centre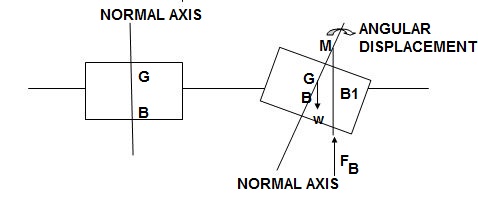
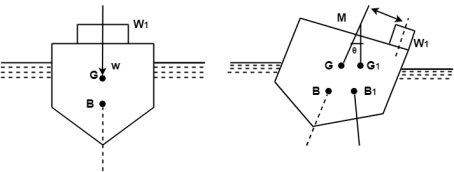
Consider a body that is afloat in a liquid. Assume the body is in equilibrium, with G representing the centre of gravity and B representing the centre of buoyancy.
As indicated in fig. 1, give the body a modest angular displacement in the clockwise direction. The centre of buoyancy, which is the centre of the displaced liquid or the centre of gravity of the body section submerged in liquid, will be shifted right from the normal axis.
As indicated in Figure, place it at B1. According to M, the line of action of the buoyancy force will intersect the normal axis of the body at some point in this posture. Meta-centre is the name given to this point M.
Meta-Centric Height
The distance MG, the distance between the meta-centre of a floating body and the centre of gravity of the body is called Meta-centric height.
Analytical method
Refer figure below it shows the tilted position of the floating body, the line L’ON’ represents the water surface.
The portion N’ON of the body is submerged and the portion L’OL is lifted because of tilting.
As a result of this, the centre of buoyancy changes its position from B to B1.
The intersection of axis of the body and the vertical line through B1, locates the metacentre, M of the body.
To find the metacentre height GM consider an elementary cylindrical prism QQ’ of portion N’ON at a distance ‘x’ from O.
Let the area of this elementary prism be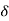 
A.
The height of this elementary prism is given by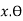 
The volume of this elementary prism is given by
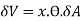
The upward force or buoyancy for acting at this prism (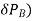
is given by
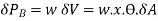
The moment of this buoyancy force about O
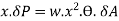
For the total portion N’ON, this moment is given by
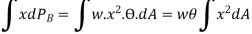
Or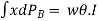 
Where I = moment of inertia of the sectional area at the waterline about the axis through O.
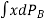gives the change in moment due to buoyancy.
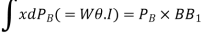
(Where PB = the total force of buoyancy)
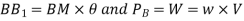
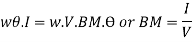
Now metacentric height, GM=BM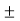 
BG
Experimental model
In this method, a known weight W1 is shifted by a distance, z across the axis of tilt.
The change of moment due to this shift is W1z
Let the angle of tilt be Ө.
This angle of tilt may be measured experimentally by using a plumb bob.
The change in moment due to this tilt is equal to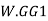 
or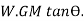 
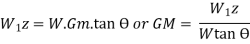
If, l = length of plumb bob, and
d = displacement of the plumb bob,
Then,
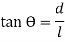
And metacentric height is given by,
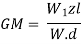
Key Takeaway:
GM=BM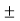 
BG
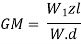
Examples
Q.1. A rectangle plane surface is 2 m wide & 3 m deep. It lies in vertical plane in water. Determine the total pressure & position of centre of pressure when its upper edge is horizontal & a) Coincides with water surface b) 2.5 m below the free water surface.
Given
b = 2m
d = 3m
a). Upper edge coincides with water surface
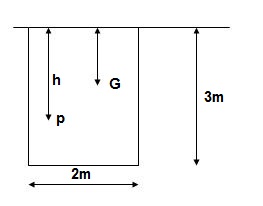
A = b x d = 2 x 3 = 6 m2
X = d/2 -3/2 = 1.5 m
Total Pressure
F = AX
= 9810 x 6 x 1.5
= 88290 N
IG = bd3/12 = 2 x 33/12 = 4.5 m4
Centre of Pressure
h = IG/AX + X = 4.5/ (6 x 1.5) + 1.5 = 2m
b). Upper edge 2.5 m below water surface
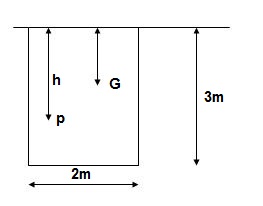
X = 2.5 + 3/2 = 4m
Total pressure F = Ax
= 9810 x 6 x 4
= 235440 N
h = IG/AX + X = 4.5/ (6 x 4) + 4 = 4.1875 m
Q.2. A heavy car plunges into a lake during an accident & land at the bottom of the lake on its wheel. The door is 1.2 m high & 1m wide, the top edge of the door is 8m below the free surface of the water. Determine total pressure acting on door approximating it as a vertical rectangular plate ¢re of pressure.
Given
b = 1 m
d = 1.2 m
A = b x d = 1 x 1.2 = 1.2 m2
X = 8 + d/2 = 8 + 1/2/2 = 8.6 m
F = AX
= 9810 x 1.2 x 8.6
= 101.24 x 103 N
IG = bd3/12 = 1 x 1.23/12 = 0.144 m4
h = IG/AX + X = 0.144/ (1.2 x 8.6) + 8.6 = 8.614 m
Q.3. A circular plate 1.5 m diameter is submerged in water with its greatest & least depth below the surface being 2 m & 0.75 m respectively. Determine total pressure ¢re of pressure.
Given
d = 1.5 m
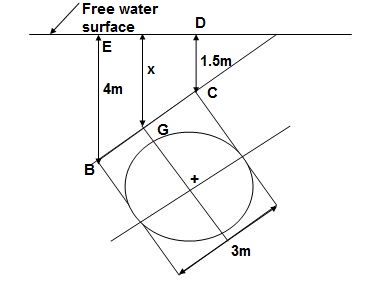
1). A = π/4 x d2 = π/4 x 1.52 = 1.767 m2
2). X = Greatest depth + Least depth / 2
= (2 + 0.75)/2 = 1.375 m
3). F = AX
= 9810 x 1.767 x 1.375
= 28.83 x 103 N
4). Sin = 1.25/1.5 = 0.833
5). IG = π/64 x d4 = π/64 x 1.54 = 0.248 m4
6). h = IG Sin2/AX + X
0.248 x 0.8332/1.767 x 1.375 + 1.375
= 1.446 m
Q.4. A triangular plate of 1m base & 1.5 m altitude is immersed in water. The plate is inclined at 300 with free water surface & base is parallel to & at a depth of 2 m from water surface. Find total pressure ¢re of pressure.
Given
b = 1 m
h = 1.5 m
= 300
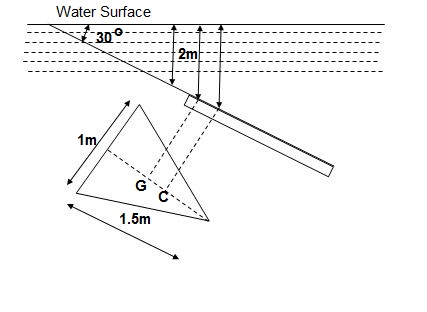
A = ½ x b x h = ½ x 1 x 1.5 = 0.75 m2
X = 2 + 1.5/3 x Sin 30 = 2.25 m
F = AX
= 9810 x 0.75 x 2.25
= 16.55 x 103 N
IG = bh3/36 = 1 x 1.53/36 = 0.09375 m4
h = IGSin2/AX + X
= 0.09375 x (Sin 30)2/0.75 x 2.25 + 2.25
= 2.264 m
Q.5. A solid cylinder of diameter 4m and height 4 m. Find the metacentric height of the cylinder if the specific gravity of cylinder is 0.6 and it is floating in water with its axis vertical. State whether the equilibrium is stable or unstable.
Given
D=4m
H=4m
S=0.6
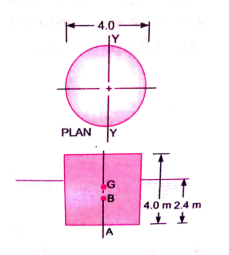
Depth of cylinder in water = 0.6H = 0.6(4) = 2.4m
Distance of centre of buoyancy(B) from A
AB = 2.4 / 2 = 1.2m
Distance of centre of gravity (G) from A
AG = H / 2 = 2m
BG = AG – AB = 2 – 1.2 = 0.8m
I =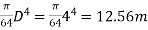 
4
V = Volume of cylinder in water
=
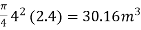
Metacentric height GM = (I / V) – BG
= (12.56/30.16) – 0.8
= -0.383 m
Negative sign means that the metacentre M is below the centre of gravity G. Thus, the cylinder is in unstable equilibrium.
References:
- Fluid Mechanics: Fundamentals and Applications by Y. A. Çengel and J. M. Cimbala, by McGraw-Hill
- Fundamentals of Fluid Mechanics by munson, Wiley India Pvt. Ltd
- Fluid Mechanics by Frank M. White, mcgraw Hill Publishing Company Ltd.
- Fluid Mechanics and Hydraulic Machines by R.K. Bansal, Laxmi Publications
