Unit - 3
Z-Transform & Inverse Z-Transform
In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation. It can be considered as a discrete-time equivalent of the Laplace transform. This similarity is explored in the theory of time-scale calculus.
Analysis of continuous-time LTI systems can be done using z-transforms. It is a powerful mathematical tool to convert differential equations into algebraic equations.
The bilateral (two-sided) z-transform of a discrete-time signal x(n) is given as
Z.T[x(n)] = X(Z) = 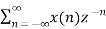
The unilateral (one sided) z-transform of a discrete time signal x(n) is given as
Z.T[x(n) = X(Z) = 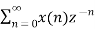
Z-transform may exist for some signals for which Discrete-Time Fourier Transform (DTFT) does not exist.
Definition
The Z-transform can be defined as either a one-sided or two-sided transform.
Bilateral Z-transform
The bilateral or two-sided Z-transform of a discrete-time signal x(n) is the formal power series X(z) defined as
X (z) = Z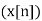 =
= 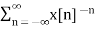
Where n is an integer and z is, in general, a complex number:
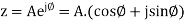
 where A is the magnitude of z,j is the imaginary unit and
where A is the magnitude of z,j is the imaginary unit and 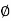 is the complex argument (also referred to as angle or phase) in radians.
is the complex argument (also referred to as angle or phase) in radians.
Unilateral Z-transform
Alternatively, in cases where x[n] is defined only for 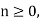 the single-sided or unilateral Z-transform is defined as
the single-sided or unilateral Z-transform is defined as
X (z) = Z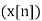 =
= 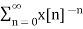
In signal processing, this definition can be used to evaluate the Z-transform of the unit impulse response of a discrete-time causal system.
An important example of the unilateral Z-transform is the probability-generating function, where the component x[n] is the probability that a discrete random variable takes the value n, and the function X(z) is usually written as X(s) in terms of s = x-1. The properties of Z-transforms (below) have useful interpretations in the context of probability theory.
Standard properties
Z-transform properties:
Z-Transform has the following properties:
1. Linearity Property
If x(n)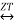 X(Z)
X(Z)
And
y(n)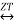 Y(Z)
Y(Z)
Then linearity property states that
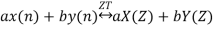
2. Time Shifting Property
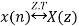
Then the time-shifting property states that
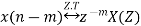
Multiplication by Exponential Sequence Property
If x(n) 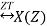
Then multiplication by an exponential sequence property is
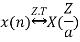
3. Time Reversal Property
If x(n) 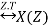
Then time reversal property states that
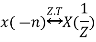
Differentiation in Z-Domain OR Multiplication by n Property
If 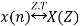
Then multiplication by n or differentiation in z-domain property states that,
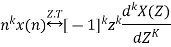
4. Convolution Property
If 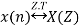
And
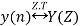
Then convolution property states that
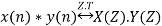
5. Correlation Property
If 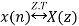
And
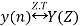
Then co-relation property states that
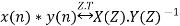
Region of Convergence (ROC) of Z-Transform
The range of variation of z for which z-transform converges is called the region of convergence of z-transform.
Properties of ROC of Z-Transforms
- ROC of z-transform is indicated with a circle in z-plane.
- ROC does not contain any poles.
- If x(n) is a finite duration causal sequence or right-sided sequence, then the ROC is entire z-plane except at z = 0.
- If x(n) is a finite duration anti-causal sequence or left-sided sequence, then the ROC is the entire z-plane except at z = ∞.
- If x(n) is an infinite duration causal sequence, ROC is the exterior of the circle with radius a. i.e. |z| > a.
- If x(n) is an infinite duration anti-causal sequence, ROC is the interior of the circle with radius a. i.e. |z| < a.
- If x(n) is a finite duration two sided sequence, then the ROC is entire z-plane except at z = 0 & z = ∞.
Some standard formulae-
1. 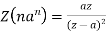
2. 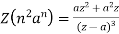
3. 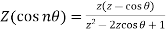
4. 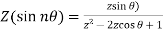
5.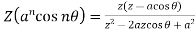
6. 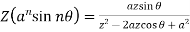
Example-1: Find Z-transform of the following functions-
(i) 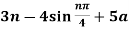
(ii) 
Sol. (i) 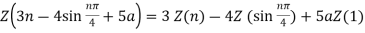
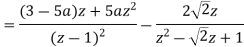
(ii) 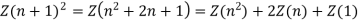
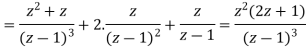
Example-2: Find Z-transform of the following functions-
(i) 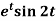
(ii) 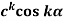
Sol. (i) As we know that-
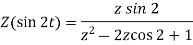
So that-
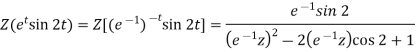
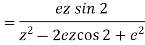
(ii) we know that-
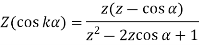
So that-
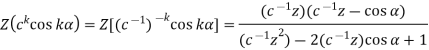
ZT of standard sequences and their inverses
Sequence | z-transformation |
 | 1 |
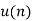 | 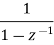 |
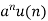 | 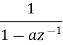 |
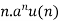 | 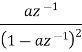 |
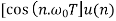 | 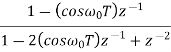 |
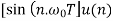 | 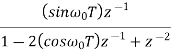 |
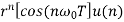 | 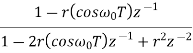 |
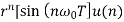 | 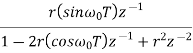 |
Example 1:
Find the z-transformation of the following left-sided sequence
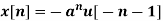
Solution:
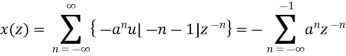
= 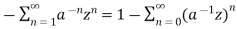
= 1- 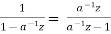
= 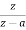
If 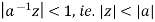
Example 2:
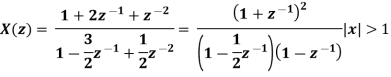
Solution:
Long division method to obtain 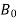
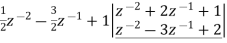 2
2
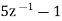
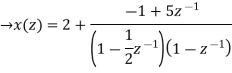
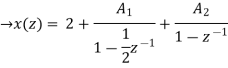
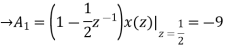
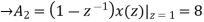
Now x(z) can be written as,
X(z) = 2-
Key takeaways:
1. The bilateral (two-sided) z-transform of a discrete-time signal x(n) is given as
Z.T[x(n)] = X(Z) = 
2. The unilateral (one sided) z-transform of a discrete time signal x(n) is given as
Z.T[x(n) = X(Z) = 
1. 
2. 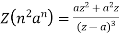
3. 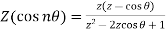
4. 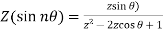
5.
6. 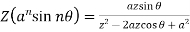
Inverse Z-transform is denoted by 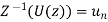 determines the sequence
determines the sequence
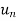 which generates the given Z-transform.
which generates the given Z-transform.
Here we will discuss two methods to evaluate inverse Z- Transforms.
Important inverse Z-Transforms:
U(z) | Inverse Z-Transform- 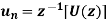 |
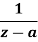 | 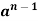 |
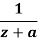 | 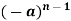 |
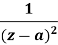 | 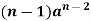 |
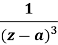 | 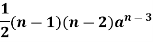 |
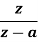 | 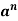 |
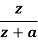 | 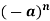 |
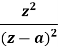 | 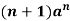 |
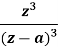 | 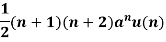 |
Power series method:
This method is considered as the simplest method for evaluation of Z-Transforms.
If U(z) is expressed as the ratio of two polynomials which can not be factorized, we simply divide the numerator by the denominator and take the inverse Z- Transform of each term in the quotient.
Example: Find the Z-Transform of log (z / z + 1) by using power series method.
Sol:
Taking, z = 1/t, U(z) = 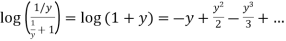
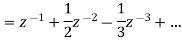
Thus
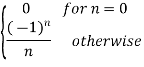
Example: Find the Z-Transform of 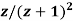 by using division method.
by using division method.
Sol:
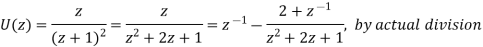
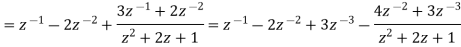
Continuing this process of division, we obtain an infinite series,
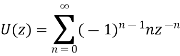
Thus
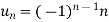
Partial fraction method:
This method involves the decomposition of U(z)/z into partial fractions, multiplying the resulting expansion by z and then inverting the same.
Example: Find the Z-Transform of 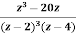
Sol:
Writing,
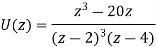
As
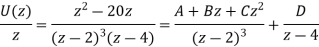
We get D = ½. Multiplying throughout by 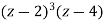 , we get
, we get
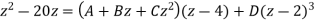
Putting z = 0, 1, -1 successively and solving the resulting simultaneous equations, we get
A = 6, B = 0 and C = ½
Thus
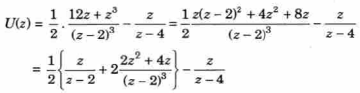
On inversion, we get
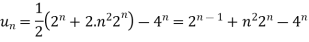
Key takeaways:
Inverse Z-transform is denoted by 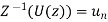
Initial Value Theorem
If X+(z) = Z{x(n)} then x(0) = lim z->∞ X+(z)
Proof:
X+(z) = 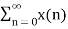 z-n
z-n
As z-> ∞ all the terms vanish except x(0) which proves the theorem
Ie
Lim z-> ∞ X+(z) = lim z-> ∞ 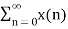 z-n = x(0)
z-n = x(0)
Final Value Theorem
If X+(z) = Z{x(n)} where ROC for X+(z) includes but is not necessarily confined to |z| >1 and (z-1) X+(z) has no poles on or outside the unit circle then
x(∞) = Lim z->1 (z-1) X+(z)
Z{ x(n+1) – Z{x(n)} = Lim k-> ∞ 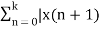 - x(n)]z-n
- x(n)]z-n
Z X+(z) – z x(0) – X+(z) = Lim k-> ∞ 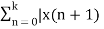 - x(n)]z-n
- x(n)]z-n
(z-1) X+(z) – zx(0) = Lim k-> ∞ 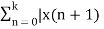 - x(n)]z-n
- x(n)]z-n
Let z-> 1 we get
Lim z->1 (z-1) X+(z) – zx(0) = Lim k-> ∞ 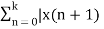 - x(n)]
- x(n)]
Lim z->1 (z-1) X+(z) – x(0) = Lim n-> ∞ { [x(1) -x(0)] + [x(2) -x(1)] +……+[x(n+1)-x(n)]}
= x(∞) – x(0)
Therefore,
x(∞) = limz->1 (z-1) X+(z)
This can be written as
x(∞) = lim z->1 (1-z-1) X(z)
This theorem enables us to find the steady state of x(n) without solving the entire sequence.
Find the z-transform of x(n) = [3(3) n – 4(2) n ] u(n)
X(z) = 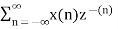
= 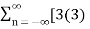 n – 4(2) n ] u(n) z -n
n – 4(2) n ] u(n) z -n
= 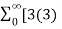 n – 4(2) n ] u(n) z -n
n – 4(2) n ] u(n) z -n
=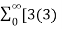 n z -n -
n z -n - 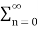 4(2) n ] z -n
4(2) n ] z -n
=3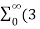 z -1 ) n – 4
z -1 ) n – 4 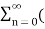 2 z -1 ) n
2 z -1 ) n
The first power series converges when |3z -1| <1 that is |z| > 3 . The second power series converges when |2z-1| <1 or |z| >2. Hence X(z) converges for |z|>3 .
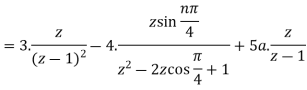
Now X(z) = 3/1-3z-1 -4/1-2z-1
= 3z/z-3 – 4z/z-2
Find the z transform of x(n) = cos n 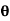 u(n)
u(n)
X(z) = 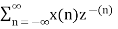
= 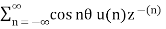
= 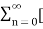 ejn
ejn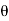 + e-jn
+ e-jn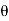 /2] z -n
/2] z -n
= ½ [ 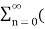 e j
e j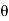 z -1 ) n +=
z -1 ) n +=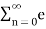 -j
-j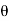 z -1 ) n ]
z -1 ) n ]
Both the series converges if [ e j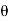 z-1| <1 and | e j
z-1| <1 and | e j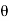 z -1 | <1 which implies |z|>1
z -1 | <1 which implies |z|>1
Now X(z) = ½ [ 1/1 – e j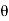 z -1 + 1/ 1 – e -j
z -1 + 1/ 1 – e -j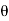 z -1 ]
z -1 ]
= ½ [ 1 – e -j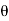 z -1 + 1 – e j
z -1 + 1 – e j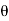 z -1 / 1 – e j
z -1 / 1 – e j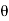 z -1 – e -j
z -1 – e -j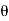 z -1 + z -2
z -1 + z -2
e j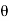 + e -j
+ e -j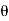 = 2 cos
= 2 cos 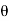
= ½ [ 2 – 2 z -1 cos 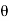 / 1 – 2 z-1 cos
/ 1 – 2 z-1 cos 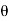 + z -2 ]
+ z -2 ]
= 1-z-1 cos 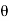 / 1 – 2 z-1 cos
/ 1 – 2 z-1 cos 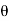 + z -2
+ z -2
Find the z transform of the sequence x(n) = n u(n)
The z-transform of unit step sequence is given by
Z{u(n)} = z/z-1
Z{ n u(n)} = -z d/dz (z/z-1)
= z/(z-1)2
Determine the z-transform of the signal
x(n ) = rn (sin w0n ) u(n)
Z{(sin w0n ) u(n)} = sin w0 z-1/ 1 -2 (cos w0) z-1 + z-2
Z{ an x(n)} = X(a-1 z)
Therefore
Z{ rn sin(w0n) u(n) } = (sin w0) (r-1 z)-1/ 1- 2 (cos w0)(r-1z)-1 + (r-1z)-2
= r(sinw0) z-1/ 1-2r(cos w0) z-1 + r2 z-2
Determine the signal x(n) whose z-transform is given by
X(z) = log(1- az-1)
X(z)= log(1-az-1)
Differentiating both sides we get
d/dz X(z) = 1/1-az-1 (a z-2) = az-2/1- az-1
-z d/dz { X(z)} = -az-1/1-az-1
= -az-1[ 1/1-az-1]
= -a Z[ a n-1 u(n-1)] -------- (1)
From differentiation property
Z{ n x(n)} = -z d/dz [ X(z)] ------- (2)
Comparing (1) and (2) we get
n x(n) = -a [ a n-1 u(n-1)]
Or x(n) = -a [a n-1 u(n-1)]/n
Determine the z-transform of the signal
x(n) =1/2 (n2 + n) (1/3) n-1 u(n-1)
=½ n2 (1/3) n-1 u(n-1) +1/2 n (1/3) n-1 u(n-1)
We know that
Z[(1/3) n u(n)] = z/ z-1/3
Using time-shifting property
Z{(1/3) n-1 u(n-1)] = 1/ z- 1/3
Z [ n (1/3) n-1 u(n-1)] = -z d/dz [1/z-(1/3)]
=-z d/dz( 1/z-1/3)= -z [-1/(z-1/3) 2]= z/ (z-1/3)2
Z [ n2 (1/3) u(n-1)] = -z d/dz [ z/(z-1/3)2]
= z(z+1/3)/(z-1/3)2
= -z [ (z-1/3)2 -2z(z-1/3)/(z-1/3)4
= z(z+1/3)/(z-1/3)3
X(z) = ½[z(z+1/3)/(z-1/3)3 + z/ (z-1/3)2]
= z2/(z-1/3)3
Final Value Theorem
If X+(z) = Z{x(n)} where ROC for X+(z) includes but is not necessarily confined to |z| >1 and (z-1) X+(z) has no poles on or outside the unit circle then
x(∞) = Lim z->1 (z-1) X+(z)
Key takeaways:
- Initial Value Theorem
If X+(z) = Z{x(n)} then x(0) = lim z->∞ X+(z)
2. Final Value Theorem
If X+(z) = Z{x(n)} where ROC for X+(z) includes but is not necessarily confined to |z| >1 and (z-1) X+(z) has no poles on or outside the unit circle then
x(∞) = Lim z->1 (z-1) X+(z)
Statement:
According to the convolution theorem if 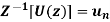 and
and 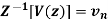 then
then

Proof:
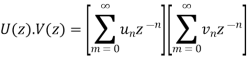
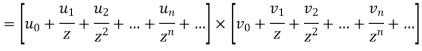
Collecting the coefficients of 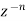
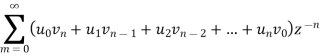
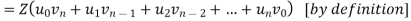
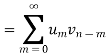
Taking inverse Z-transform the result follows
Note- Convolution theorem plays an important role in the solution of difference equations and in probability problems involving sums of two independent random variables.
Region of convergence (R.O.C.)-
The region of convergence of Z-transform is the region in the z-plane where the infinite series convergence absolutely.
Thus the region of convergence of a one-sided Z-transform
Of a right-sided sequence, which means,

Is |z| > a i.e., the exterior of the circle with centre at origin and of radius a.
Similarly the region of convergence (ROC) of
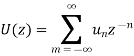
Is the annulus region a < |z| < b.
Example: Evaluate by using convolution theorem.
Sol:
We know that,
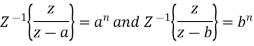
So that,
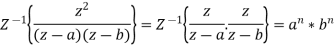
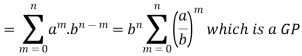
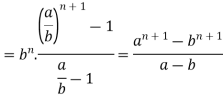
Key takeaways:
- If
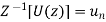 and
and 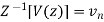 then
then
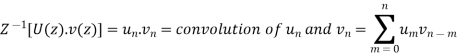
2. Convolution theorem plays an important role in the solution of difference equations and in probability problems involving sums of two independent random variables.
The solution of difference equations
Working procedure to solve the linear difference equation by ZT-
1. Take the ZT of both sides of the differential equations.
2. Transpose all terms without U(z) to the right
3. Divide by the coefficients of U(z)
4. Express this function in terms of the Z-transform of the known function and take the inverse ZT of both sides.
This will give 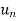 as a function of n, is the required solution.
as a function of n, is the required solution.
Example 1:
Solve the differential equation 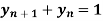 by the z-transformation method.
by the z-transformation method.
Solution:
Given,
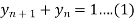
Let y(z) be the z-transform of 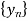
Taking z-transforms of both sides of eq(1) we get,
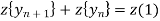
Ie. 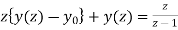
Using the given condition, it reduces to
(z+1)y(z) = 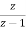
i.e.
Y(z) = 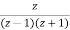
Or Y(Z) = 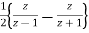
On taking inverse Z-transforms, we obtain
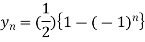
Example 2:
Solve 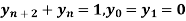 using z-transforms
using z-transforms
Solution:
Consider,
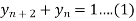
Taking z-transforms on both sides, we get
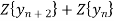 =
=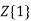
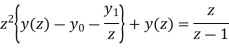
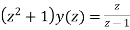 or
or
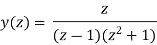
Now,
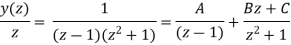
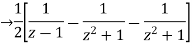
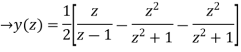
Using inverse z-transform we obtain,
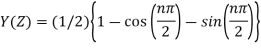
Example-3:
Solve the following by using Z-transform
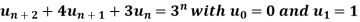
Sol. If 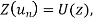 then
then 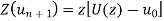
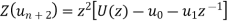
And
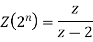
Now taking the Z-transform of both sides, we get
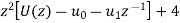 z[
z[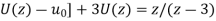
It becomes-
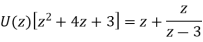
So,
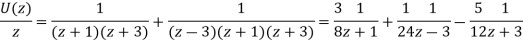
Now-
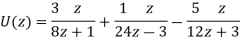
On inversion, we get-
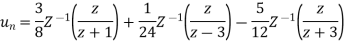
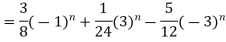
References:
1. R. J. Beerends H. G. Ter Morsche, J. C. Van Den Berg. L. M. Van De Vrie, Fourier and Laplace Transforms, Cambridge University Press.
2. Sastry S.S. Introductory Methods of Numerical Analysis, PHI.
3. B.S. Grewal: Higher Engineering Mathematics; Khanna Publishers, New Delhi.
4. B.V. Ramana: Higher Engineering Mathematics; Tata McGraw- Hill Publishing Company Limited, New Delhi.
5. Peter V.O’ Neil. Advanced Engineering Mathematics, Thomas (Cengage) Learning.