Unit - 5
Second law
Heat engines
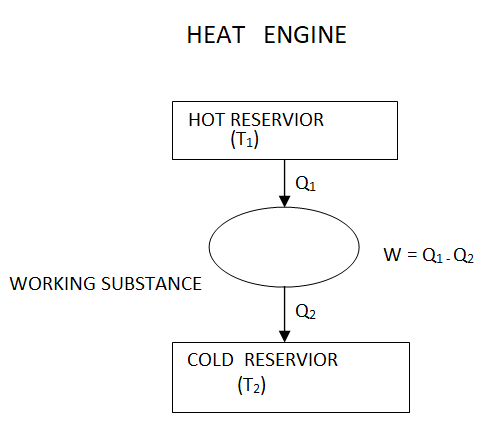
In a thermodynamic cycle net heat transfer takes place to the system and a net-work transfer from the system. A heat engine executes Heat Engine cycle. Its Working Fluid may be in the form of Gas or Liquid.
It receives heat from heat source and produces the mechanical work and remainder of energy is rejected to heat sink.
“The heat engine is a device that transfers energy from an object at a higher temperature to an object at a lower temperature when work is done on the system.”
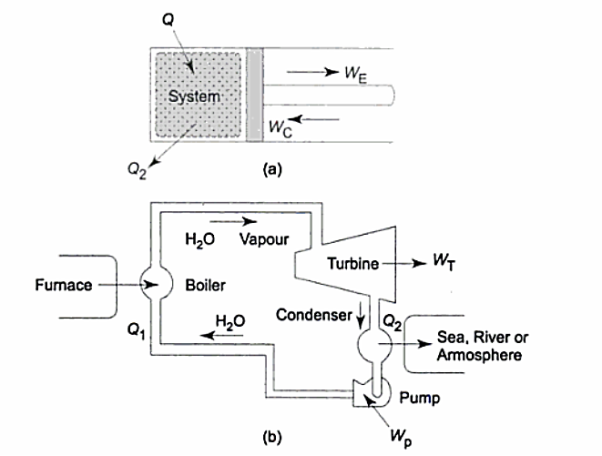
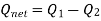
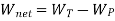
As, 
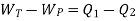
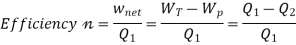
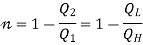
Or
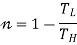
Example of Heat Engine:
- Gasoline and diesel engines
- Jet engines
- Steam turbines
Reversed Heat engines
The reverse heat engine is a device that transfers energy from an object at a lower temperature to an object at a higher temperature by doing work on the system.
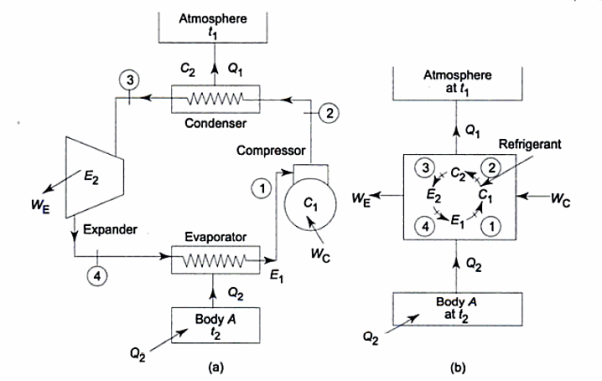
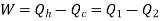
There are two Types of Reversed Heat Engine explained below.
Heat Pump
It utilizes heat transfer from Low to High Temperature. i.e., Qc = Q2 and delivers Qh = Q1. This requires work input, as Temp is flowing from Cold to Hot. Which produces Heat Transfer. Qc comes from outside air (Temp below freezing to Indoor Space)
Compressor raises the temperature & pressure of gas and forces it into condenser coils, that are inside the heated space. The Gas is converted into Liquid. Liquid flows back through expansion valve (Pressure Reducing). Liquid when cooled through expansion returns to outer evaporator.
Compressor squeeze gas particles, leading to generation of high pressure. So, temperature also increases. These gas particles pass through tubes which comes in contact with outer air. The gas cools & condensates, which goes into evaporator through expansion valve. Gas spreads out and pressure drops, leading to increase in temperature. A fan blows over this.
Here, Efficiency is Measured through Coefficient of Performance.
Quality of Heat pump is judged by how much energy is transferred by heat into warm space (Qh). Compared with how much input work (W) is required.
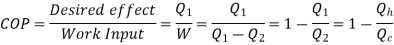
Refrigerator
The functioning Is same as Heat Pump, But the difference is
Air Conditioner = “Heat is transferred outdoors from inside a room “.
Refrigerator = ‘Heat is moved out of the inside into surrounding”
Quality of Refrigerator/AC is judged by how much energy is removed by heat Qc from cold, compared with how much work (W) is required.
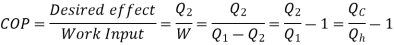
Key Takeaways:
- For hear engine
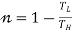
- For heat Pump
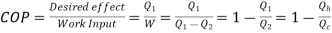
- For Refrigerator
The thermal efficiency of a device that uses thermal energy, such as an internal combustion engine, a steam turbine or a steam engine, a boiler, furnace, or a refrigerator, is a dimensionless performance metric in thermodynamics. Thermal efficiency is the proportion of the energy added by heat (primary energy) that is transformed to net-work output in a heat engine (secondary energy). Thermal efficiency is the ratio of net heat production for heating or removal for cooling to energy input in the case of a refrigeration or heat pump cycle (the coefficient of performance)
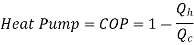
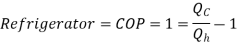
The second law of thermodynamics has two statements put forward by two scientists.
- Clausius statement: “It is impossible for a self-acting machine working in a cyclic process unaided by any external agency, to convey heat from a body at a lower temperature to a body at a higher temperature”. In other words, heat cannot flow from a colder to a hotter body.
2. Kelvin Planck statement: “It is impossible to construct an engine, which while operating in a cycle produces no other effect except to extract heat from a single reservoir and do equivalent amount of work”.
i.e., “A heat engine can never be 100% efficient,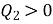 
. Which means always there a heat rejection.
If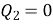 
means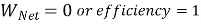 
. i.e., Only 1 Reservoir is working. Which violates Kelvin-Plank Statement. This is Known as PMM 2.
Although the Clausius and Kelvin-Planck statements appear to be different, they are equivalent in the sense that a violation of either statement implies violation of other.
Equivalence of Clausius Statement to the Kelvin-Planck Statement :
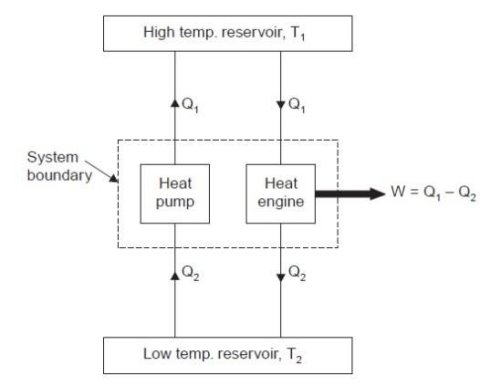
Consider a higher temperature reservoir T1 and low temperature reservoir T2. Fig. Shows a heat pump which requires no work and transfers an amount of Q2 from a low temperature to a higher temperature reservoir (which is a violation of the Clausius statement).
Let an amount of heat Q1 (greater than Q2) be transferred from high temperature reservoir to heat engine which develops a net-work, W = Q1 – Q2 and rejects Q2 to the low temperature reservoir. Since there is no heat interaction with the low temperature, it can be eliminated. The combined system of the heat engine and heat pump acts then like a heat engine exchanging heat with a single reservoir, which is the violation of the Kelvin-Planck statement.
The reversible process is an ideal process that never occurs, whereas the irreversible process is a natural process that occurs frequently in nature. When we tear a page from a book, we can't go back and 'un-tear' it. This is an irreversible process. Water can be condensed in the form of rain when it evaporates. This is a process that can be reversed.
Reversible Process
A thermodynamic process is reversible if it can be reversed in such a way that both the system and its surroundings return to their original states, with no other changes occurring anywhere else in the universe. It means that at the end of the reverse process, both the system and its surroundings are returned to their initial states.
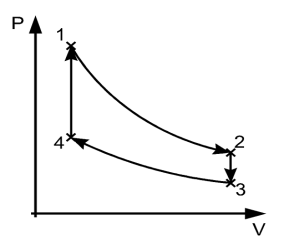
In the figure above, the system has undergone a change from state 1 to state 2. The reversible process can reverse completely and there is no trace left to show that the system had undergone thermodynamic change. During the reversible process, all the changes in state that occur in the system are in thermodynamic equilibrium with each other.
Internally reversible process
If no irreversibility’s occur within the system's boundaries, the process is internally reversible. A system goes through a series of equilibrium states in these processes, and when the process reverses, the system goes through exactly the same equilibrium states while returning to its initial state.
Externally reversible process
No irreversibility’s occur outside the system boundaries during an externally reversible process. Heat transfer between a reservoir and a system is an externally reversible process if the system and reservoir have the same temperature at the point of contact.
A process can be reversible only when its satisfying two conditions
- Dissipative force must be absent.
- The process should occur in infinite small time.
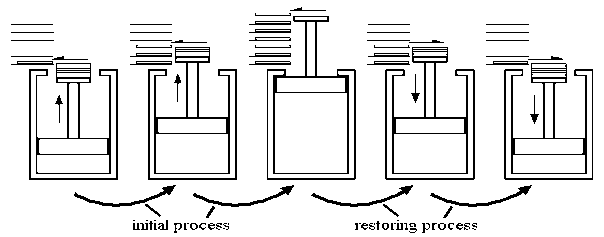
In layman's terms, a reversible process is one that can be completely reversed. This means that the system's final properties can be perfectly reversed back to the original properties. Only if the changes in the process are infinitesimally small can the process be perfectly reversible. Because it is impossible to trace these extremely small changes in such a short period of time in practise, the reversible process is also an ideal process. The changes that take place during the reversible process are in balance with one another.
Irreversible Process
Irreversible processes occur as a result of deviating from the curve, which reduces the amount of overall work done. An irreversible process is one that deviates from equilibrium in thermodynamic terms. In terms of pressure and volume, it occurs when the pressure (or volume) of a system change so dramatically and instantly that the volume (or pressure) does not have time to stabilise.
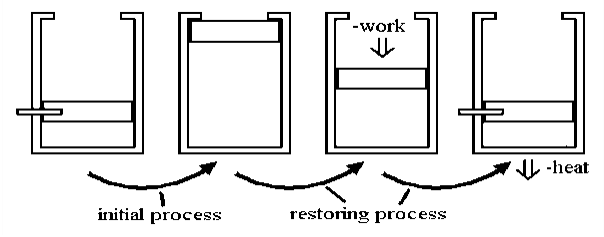
Allowing a certain volume of gas to escape into a vacuum is a classic example of an irreversible process. The system and surroundings are not in equilibrium during the expansion process because pressure is released on a sample, and it is allowed to occupy a large space. Little work is done here. However, significant work is required, along with a corresponding amount of energy dissipation as heat flows to the environment. This is done to reverse the process.
THE CARNOT VAPOR CYCLE
The Carnot cycle is the most efficient cycle when operating between two temperatures. As a result, it is natural to consider the Carnot cycle first as a potential ideal cycle for vapour power plants.
The Carnot cycle, on the other hand, is not a good model for power cycles.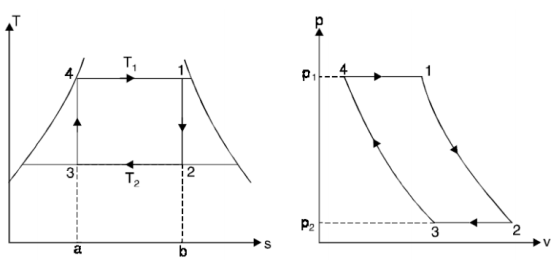
- Process 4-1: 1 kg of boiling water at temperature T1 is heated to form wet steam of dryness fraction x1. Thus, heat is absorbed at constant temperature T1 and pressure p1 during this operation.
- Process 1-2: steam is expanded isentropically to temperature T2 and pressure p2. The point ‘2’ represents the condition of steam after expansion.
- Process 2-3: heat is rejected at constant pressure p2 and temperature T2. As the steam is exhausted it becomes wetter and cooled from 2 to 3.
- Process 3-4: the wet steam at ‘3’ is compressed isentropically till the steam regains its original state of temperature T1 and pressure p1.
Thus, cycle is completed.
Net work done = Heat supplied – heat rejected
= T1 (s2 - s3) - T2 (s2 - s3) = (T1 – T2) (s2 - s3)
Carnot Efficiency η = Work done / Heat supplied = (T1 – T2) (s2 - s3) / T1 (s2 - s3) = (T1 – T2) / T1
Limitations or Impracticalities of Carnot Cycle:
Though Carnot cycle is simple (thermodynamically) and has the highest thermal efficiency for given values of T1 and T2, yet it is extremely difficult to operate in practice because of the following reasons:
- It is difficult to compress a wet vapour isentropically to the saturated state as required by the process 3-4.
- It is difficult to control the quality of the condensate coming out of the condenser so that the state ‘3’ is exactly obtained.
- The efficiency of the Carnot cycle is greatly affected by the temperature T1 at which heat is transferred to the working fluid. Since the critical temperature for steam is only 374°C, therefore, if the cycle is to be operated in the wet region, the maximum possible temperature is severely limited.
- The cycle is still more difficult to operate in practice with superheated steam due to the necessity of supplying the superheat at constant temperature instead of constant pressure.
Some of these problems could be eliminated by executing the Carnot cycle in a different way, as shown in Fig. B.
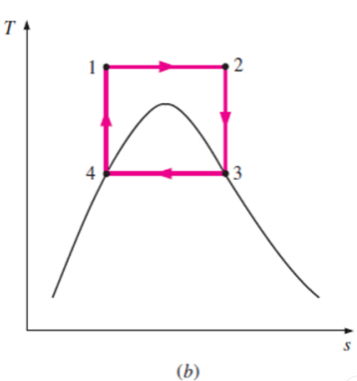
This cycle, on the other hand, has additional issues, such as isentropic compression to extremely high pressures and isothermal heat transfer at variable pressures.
As a result, we conclude that the Carnot cycle is not a realistic model for vapour power cycles and cannot be approximated in actual devices.
Carnot engine
A Carnot engine, also known as a Carnot heat engine, is an idealised engine whose operation is completely reversible. To complete one cycle, this engine employs an ideal gas as the working substance and employs a 4-stroke process.
It takes heat Q1 from source and rejects heat Q2 to sink and performing an amount of work W=Q1−Q2
The Carnot's engine is a reversible engine working between two temperature limits.
The complete cycle functions are given below
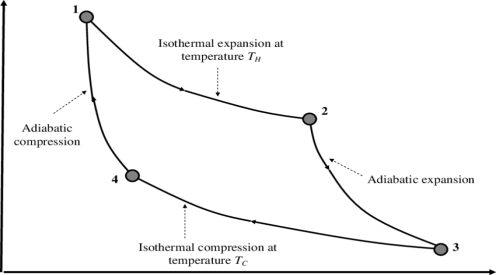
P-V Diagram
1) Reversible Isothermal expansion heat addition at the constant temperature T1 or TH
2) Reversible Adiabatic expansion of ideal gas. In this process, the temperature of the ideal gas falls from source temperature T1 to sink temperature T2.
3) Reversible Isothermal compression of ideal gas at sink temperature T2 or TC. In doing so, it rejects heat Q2 to the sink.
4) Reversible Adiabatic compression of ideal gas where the temperature naturally raises from T2 to T1 and thus the working substance returns to its original state completing the cycle.
The efficiency is given as
η= Work done / Heat input
Thus, W=Q1−Q2 and heat input is obviously Q1
This gives, η= W/Q1
=1−Q2/Q1
It may be shown thermodynamically that Q2/Q1 = T2/T1.
Key takeaways
1) The Carnot's engine is a reversible engine working between two temperature limits.
2) The efficiency is given as
η= Work done / Heat input
Thus, W=Q1−Q2 and heat input is obviously Q1
This gives, η= W/Q1
=1−Q2/Q1
The working medium has not been mentioned in the Carnot cycle considerations in this section. As a result, they are not limited to an ideal gas and can hold for Carnot cycles in any medium. We previously calculated the Carnot efficiency using an ideal gas as a medium, and the temperature definition used in the ideal gas equation was not critical to the thermodynamic arguments. We can define a thermodynamic temperature scale that is independent of the working medium in more detail. Consider the situation depicted in the diagram below. Figure 6.2, which includes three reversible cycles T1 has a high temperature heat reservoir and T3 has a low temperature heat reservoir. The ratio of the magnitudes of the heat absorbed and rejected in a Carnot cycle has the same value for all systems for any two temperatures T1, T2.
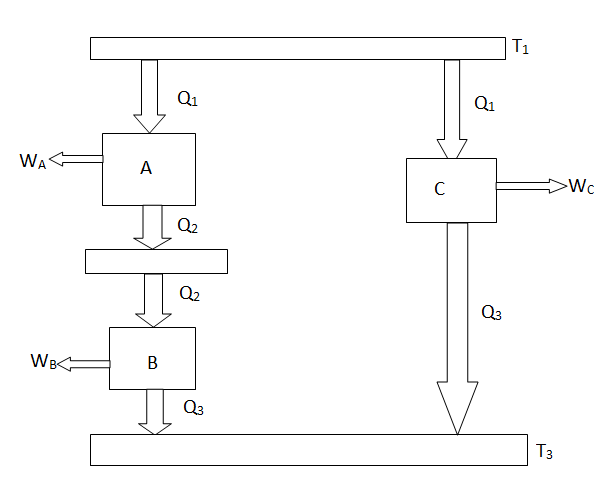
Figure 5: Arrangement of heat engines to demonstrate the thermodynamic temperature scale
We choose the cycles so Q1is the same for A and C. Also, Q3 is the same for B and C. For a Carnot cycle
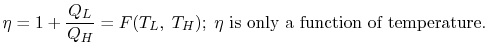
Also
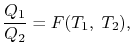
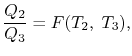
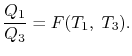
But
Hence
We thus conclude that F (T1,T2) has the form f(T1)/f(T2) and
Similarly F (T2,T3)= f(T2)/f(T3). The ratio of the heat exchanged is therefore
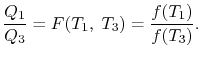
In general,
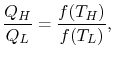
As a result, the ratio of heat exchanged varies with temperature. We could choose any monotonic function, and one option is the simplest: T = f (T) This is the thermodynamic temperature scale, QH/QL = TH/TL. The temperature defined in this way is the same as the temperature of an ideal gas; the thermodynamic temperature scale and the ideal gas scale are equivalent.
References:
- Basic and Applied Thermodynamics by PK Nag, MCGRAW HILL INDIA.
- Thermodynamics for Engineers by Kroos & Potter, Cengage Learning.
- Thermodynamics by Shavit and Gutfinger, CRC Press.
- Thermodynamics- An Engineering Approach by Cengel, MCGRAW HILL INDIA.
- Basic Engineering Thermodynamics, Joel, Pearson.
