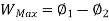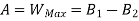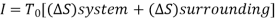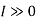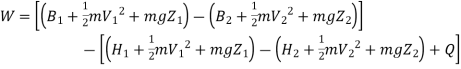Unit - 6
Clausius inequality
CLAUSIUS INEQUALITY:
The integral of dQ / T is always less than or equal to zero.
∮ dQ / T ≤ 0
This inequality holds true for all cycles in the universe, with no exceptions.
Consider a system connected to a thermal energy reservoir at a constant thermodynamic (i.e., absolute) temperature of TR via a reversible cyclic device to demonstrate the validity of the Clausius inequality.
The cyclic device receives heat ∂QR from the reservoir and supplies heat Q to the system, the temperature at the boundary being T (a variable), while producing work ∂Wrev.
The system produces work ∂Wsys as a result of this heat transfer.
Balancing the combined system identified by dashed lines yield
ΔWc = δQR - dEc
Considering that the cyclic device is a reversible one, we have
δQR / TR = δQ / T
Eliminating ∂QR from the two relations above yields
ΔWc = TR δQ / T - dEc
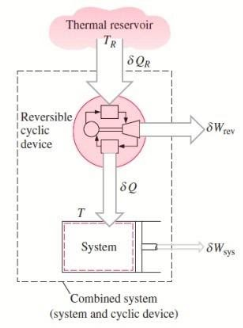
We let the system go through one cycle while the cyclic device goes through an integral number of cycles. The preceding relationship then becomes
Wc = TR ∮ dQ / T
The net work for the combined cycle is represented by ∂WC, which is the cyclic integral of WC.
During a cycle, it appears that the combined system exchanges heat with a single thermal energy reservoir while involving (producing or consuming) work Wc. We reason that Wc cannot be a work output and thus cannot be a positive quantity based on the Kelvin-Planck statement of the second law, which states that no system can produce a net amount of work while operating in a cycle and exchanging heat with a single thermal energy reservoir.
∮ dQ / T ≤ 0
Entropy
Clausius realized in 1865 that he had discovered a new thermodynamic property and he chose to name this property entropy. It is designated S and is defined as , dS = (dQ / T)
The entropy changes of a system during a process can be determined by integrating above Eq. Between the initial and the final states
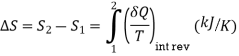
Therefore, the entropy of a substance can be assigned a zero value at some arbitrarily selected reference state, and the entropy values at other states can be determined from above Eq
Entropy is defined as a measure of randomness or disorder of a system. Aside from the general definition, there are several definitions for this concept. We do not consider the microscopic details of a system from the standpoint of entropy in thermodynamics. Entropy, on the other hand, is used to describe a system's behaviour in terms of thermodynamic properties such as temperature, pressure, entropy, and heat capacity. This thermodynamic description considered the systems' state of equilibrium. Meanwhile, the statistical definition developed later focused on the thermodynamic properties defined in terms of the statistics of a system's molecular motions. The entropy of a molecular system is a measure of its disorder.
Entropy—a Property of a System
- Let us consider a system undergoing a reversible process from state 1 to state 2 along path L and then from state 2 to the original state 1 along path M or N.
- Applying the Clausius theorem to this reversible cyclic process
∮ dQ / T = 0
- For cycle 1-L-2-M-1, we have
- For cycle 1-L-2-N-1
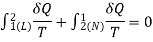
- Subtracting equation (2) from equation (1), we have
- As no restriction is imposed on paths L and M, except that they must be reversible, the quantity is a function of the initial and final states of the system and is independent of the path of the process.
- Hence it represents a property of the system.
- This property is known as the “entropy”.
THE INCREASE OF ENTROPY PRINCIPLE
- Consider a cycle that is made up of two processes:
- Process 1-2, which is arbitrary (reversible or irreversible), and process 2-1, which is internally reversible, as shown in Figure.
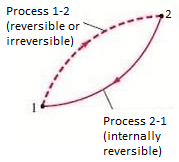
- From Clausius Inequality
∮ dQ / T ≤ 0
- The second integral in the previous relation is recognized as the entropy change S1- S2 Therefore,
DS ≥ dQ / T
Where the equality holds for an internally reversible process and the inequality for an irreversible process.
We may conclude from these equations that the entropy change of a closed system during an irreversible process is greater than the integral of ∂Q/T evaluated for that process.
The inequality sign in the preceding relations is a constant reminder that the entropy change of a closed system during an irreversible process is always greater than the entropy transfer.
That is, some entropy is generated or created during an irreversible process, and this generation is due entirely to the presence of irreversibility’s.
The entropy generated during a process is called entropy generation and is denoted by Sgen.
Noting that the difference between the entropy change of a closed system and the entropy transfer is equal to entropy generation, hence previous Eq. Can be rewritten as an equality as
Its value depends on the process, and thus it is not a property of the system. Also, in the absence of any entropy transfer, the entropy change of a system is equal to the entropy generation.
For an isolated system (or simply an adiabatic closed system), the heat transfer is zero
ΔSisolated ≥ 0
This equation can be expressed as the entropy of an isolated system during a process always increases or, in the limiting case of a reversible process, remains constant. In other words, it never decreases. This is known as the increase of entropy principle.
Note that in the absence of any heat transfer, entropy change is due to irreversibility only, and their effect is always to increase entropy.
The increase of entropy principle can be summarized as
By the Clausius definition, if an amount of heat Q flows into a large heat reservoir at temperature T above absolute zero, then the entropy increase is ΔS = Q/T. This equation effectively gives an alternate definition of temperature that agrees with the usual definition. Assume that there are two heat reservoirs R1 and R2 at temperatures T1 and T2 (such as the stove and the block of ice). If an amount of heat Q flows from R1 to R2, then the net entropy change for the two reservoirs is
The condition ΔS ≥ 0 determines the maximum possible efficiency of heat engines—that is, systems such as gasoline or steam engines that can do work in a cyclic fashion. Suppose a heat engine absorbs heat Q1 from R1 and exhausts heat Q2 to R2 for each complete cycle. By conservation of energy, the work done per cycle is W = Q1 – Q2, and the net entropy change is ∆S=Q2/T2-Q1/T1
To make W as large as possible, Q2 should be as small as possible relative to Q1. However, Q2 cannot be zero, because this would make ΔS negative and so violate the second law. The smallest possible value of Q2 corresponds to the condition ΔS = 0, yielding (Q2/Q1) MIN=T2/T1as the fundamental equation limiting the efficiency of all heat engines. A process for which ΔS = 0 is reversible because an infinitesimal change would be sufficient to make the heat engine run backward as a refrigerator.
Which is positive provided that T1 > T2. Thus, the observation that heat never flows spontaneously from cold to hot is equivalent to requiring the net entropy change to be positive for a spontaneous flow of heat. If T1 = T2, then the reservoirs are in equilibrium, no heat flows, and ΔS = 0.
Properties of Entropy
- It is a thermodynamic function.
- It is a state function. It depends on the state of the system and not the path that is followed.
- It is represented by S but in the standard state, it is represented by S°.
- It’s SI unit is J/Kmol.
- It’s CGS unit is cal/Kmol.
- Entropy is an extensive property which means that it scales with the size or extent of a system.
- Entropy order: gas>liquid>solids
Entropy Change and Calculations
During entropy change, a process is defined as the amount of heat emitted or absorbed isothermally and reversibly divided by the absolute temperature. Entropy formula is given as.
∆S = qrev,iso/T
If we add the same quantity of heat at a higher temperature and lower temperature, randomness will be maximum at a lower temperature. Hence, it suggests that temperature is inversely proportional to the entropy.
Total entropy change, ∆Stotal =∆Ssurroundings+∆Ssystem
Total entropy change is equal to the sum of entropy change of system and surroundings.If the system loses an amount of heat q at a temperature T1, which is received by surroundings at a temperature T2
So, ∆Stotal can be calculated
∆Ssystem=-q/T1
∆Ssurrounding=q/T2
∆Stotal=-q/T1+q/T2
●If∆Stotal is positive, the process is spontaneous.
●If∆Stotal is negative, the process is non-spontaneous.
●If∆Stotal is zero, the process is at equilibrium.
Entropy changes during the isothermal reversible expansion of an ideal gas
∆S = qrev,iso/T
According to the first law of thermodynamics,
∆U=q+w
For the isothermal expansion of an ideal gas, ∆U = 0
qrev = -wrev = nRTln(V2/V1)
Therefore,
∆S = nRln(V2/V1)
Entropy Change during Reversible Adiabatic Expansion
For an adiabatic process heat exchange will be zero(q=0), therefore reversible adiabatic expansion is taking place at a constant entropy (isentropic),
q = 0
Therefore,
∆S = 0
Even though the reversible adiabatic expansion is isentropic, irreversible adiabatic expansion is not isentropic.
∆S not equal to Zero.
Key takeaways
1) The net entropy change for the two reservoirs is
2) Total entropy change, ∆Stotal =∆Ssurroundings+∆Ssystem
3) Temperature. Entropy formula is given as.
∆S = qrev,iso/T
Entropy changes of pure substances
Because most substances' thermodynamic properties are too complex to be expressed by simple equations, they are presented in the form of tables.
Many working fluids can be used in thermo-systems. Water is one of the most commonly used working fluids. This is the only liquid in this section.
The thermodynamic properties that are commonly used are:
- Temperature (T), oC or oF
- Pressure (P), Pa or psia
- Specific volume (v) (the volume per unit mass), m3/kg or ft3/lb
- Specific internal energy (u), kJ/kg or Btu/lb
- Specific enthalpy (h), kJ/kg or Btu/lb
Specific entropy (s) (Which will be introduced in the following section), kJ/(kg-K) or Btu/(lb-R)
Saturated Liquid and Saturated Vapor
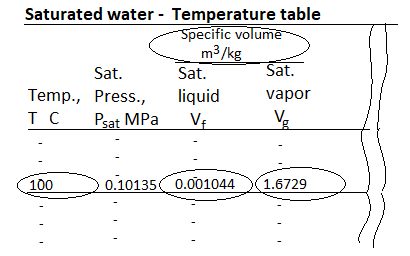
Fig: Saturated Water Table
The saturation temperature is the temperature at which a pure substance changes phase at a given pressure. Water has a saturation temperature of 100 oC at 1 atm. The pressure at which a pure substance changes phase at a given temperature is known as the saturation pressure. Water has a saturation pressure of 1 atm at 100 degrees Celsius. The saturation temperature and pressure are interdependent.
There are two kinds of saturated water tables. Both tables contain the same data. The only distinction is that the properties are listed as a function of either temperature or pressure.
The properties listed in the tables include
- Saturation pressure (Psat) for a given temperature or saturation temperature (Tsat) for a given pressure
- Specific volume of saturated liquid (vf) and saturated vapor (vg)
- Specific internal energy of saturated liquid (uf), saturated vapor (ug), and vaporization (ufg = ug - uf)
- Specific enthalpy of saturated liquid (hf), saturated vapor (hg), and vaporization (hfg = hg - hf) or latent heat of vaporization.
Specific entropy of saturated liquid (sf), saturated vapor (sg), and vaporization (sfg = sg - sf)
Saturated Mixture
During the vaporization process of water, the substance is a mixture of saturated liquid and saturated vapor. Quality (x) is defined to describe the fraction of saturated vapor in the mixture.
x = mvapor/mtotal
Where
mvapor = mass of vapor in the mixture
mtotal = total mass of the mixture
mtotal = mliquid + mvapor = mf + mg
Quality is assigned a value between 0 and 1. According to its definition, x equals 1 for saturated vapour and 0 for saturated liquid.
Saturated mixtures are biphasic systems. It can be treated as a homogeneous mixture for convenience, and the properties of this mixture are simply the average properties of the saturated liquid and saturated vapour. For instance, the specific volume of the mixture can be calculated using
Vav = Vf + Vg
mtotal vav = mf vf + mg vg
vav = mf vf/mtotal + mg vg/mtotal
= vf (1 - mg/mtotal) + vg mg/mtotal
= vf (1 - x) + vg x
= vf + vfg x
Rearranging the above equation to give an expression for the quality x as
x = (vav - vf)/vfg
Based on this equation, quality can be determined from the horizontal distance on the T-v or P-v diagram as shown in the figure.
Fig: Quality is related to the horizontal distance on T-v diagram
The above process can be repeated for u and h
uav = uf + ufg x
hav = hf + hfg x
Superheated Vapor
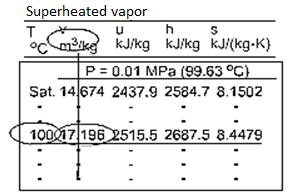
Fig: Superheated Water Table
Temperature and pressure are independent of each other because superheated vapour is a single-phase substance. The properties of superheated vapours are listed as a function of both temperature and pressure in the superheated vapour tables. Among the properties listed are v, u, h, and s. The saturation temperature for the pressure is given in parentheses after the pressure value.
Superheated vapor can be characterized by
- P <Psat at a given T
- T >Tsat at a given P
- v > vg at a given P or T
- u >ug at a given P or T
h > hg at a given P or T
Sub cooled Liquid
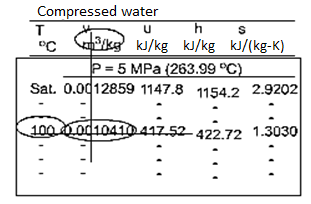
Fig: Sub cooled Water Table
The subcooled liquid water tables have the same format as the superheated vapour tables. In the absence of compressed liquid data, it is common practise to estimate the properties of compressed liquid using saturated liquid data based on the given temperature. The following approximation can be used to reduce the error for h.
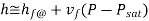
Subcooled liquid can be characterized by
- P >Psat at a given T
- T <Tsat at a given P
- v <vf at a given P or T
- u <uf at a given P or T
h <hf at a given P or T
The entropy of a pure substance is determined from tables in the same manner as other properties such as v, u, and h. The value of entropy at a specified state is determined just like any other property.
- Compressed liquid: from tables
- Saturated liquid (sf): from tables
- Saturated mixture: s = sf + xsfg
Where
x = quality
sfg = sg - sf
- Saturated vapor (sg): from tables
- Superheated vapor: from tables
If the compressed liquid data are not available, the saturated liquid at the same temperature can be used to approximate the compressed liquid's entropy.
The entropy of the isolated system is a measure of the system's irreversibility. The greater the irreversibility, the greater the entropy of the system. As a result, the reversible process is an ideal process that never occurs in reality. This means that a certain amount of irreversibility is always present in the system, and that the entropy of the isolated system is always increasing, never decreasing. Let us remember that an isolated system can always be formed by combining any system and its surroundings within a single boundary.
“An irreversible process always tends to bring the isolated system into greater disarray. An isolated system always tends to increase in entropy. The entropy of a system can be roughly defined as a measure of the degree of molecular disorder present in the system. When heat is applied to a system, the disorderly motion of the molecules increases, as does the system's entropy. When the heat is removed from the system, the opposite happens.”
The first and second law of thermodynamics can be Summarizing in Clausius two statements:
- The energy of the world (universe) is constant.
- The entropy of the world tends towards a maximum.
As a result, the entropy of the isolated system tends to increase and reaches its maximum value at the point of equilibrium. When the system reaches equilibrium, the entropy increase becomes zero.
Let a system change from state 1 to state 2 by a reversible process A and return to state 1 by another reversible process B. Then 1A2B1 is a reversible cycle. Therefore, the Clausius inequality gives:
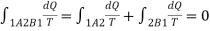
If the system is restored to the initial state from 1 to state 2 by an irreversible process C, then 1A2C1 is an irreversible cycle. Then the Clausius inequality gives:
Subtracting the above equation from the first one,
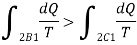
Since the process 2B1 is reversible,
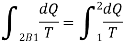
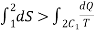
In general
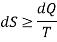
Where the equality sign indicates a reversible process and the inequality sign indicates an irreversible process.
Let us now use the above result to calculate the entropy change of the universe when a system interacts with its surroundings and exchanges energy as heat.
Let Tsur and Tsys be the temperatures of the surroundings and the system such that Tsur >Tsys Let dQ represent the energy transfer as heat from the surroundings to the system during the given irreversible process.
DSsys = dQ/Tsys
DSsur = -dQ/Tsur
DSuni = dSsys + dSsur = (dQ/T) sys - (dQ/T) sur >0
DSuni >0 (since Tsur>Tsys)
If the system is isolated, there is no change in the entropy of the surroundings and
DS = 0, for an isolated system. Therefore, the entropy of an isolated system either increases or, in the limit, remains constant.
When the system's process is reversible, the equality sign holds true; when there is any irreversibility in the process, the inequality sign holds true. This is commonly referred to as the principle of entropy increase. Irreversible or spontaneous processes can occur only in the direction that increases the entropy of the universe or an isolated system. These processes cannot occur in a decreasing entropy direction.
For an isolated system,
DS > 0, for irreversible processes
DS = 0, for reversible processes
DS < 0, the process is impossible
Property diagrams are excellent visual aids in thermodynamic process analysis. In previous chapters, we used P-v and T-v diagrams extensively in conjunction with the first law of thermodynamics. It is very useful in the second law analysis to plot the processes on diagrams with entropy as one of the coordinates. The temperature-entropy and enthalpy-entropy diagrams are two commonly used diagrams in second-law analysis. Consider the entropy defining equation (Eq). It can be rearranged as follows:
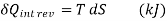…….1
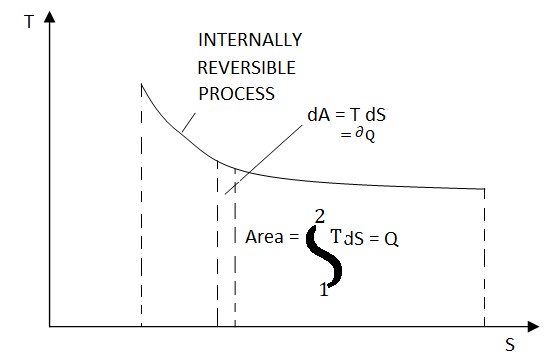
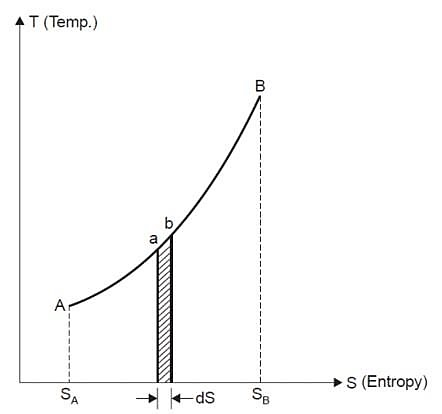
Figure: On a T-S diagram
The area under the process curve represents the heat transfer for internally reversible processes.
Equation 1as shown in Fig Qrev int corresponds to a differential area on a T-S diagram. The total heat transfer during an internally reversible process is determined by integration to be
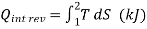….2
Equation 2 denotes the area under the process curve on a T-S diagram. As a result, we conclude that heat transfer during an internally reversible process is represented by the area under the process curve on a T-S diagram. This is similar to the area under the process curve on a P-V diagram representing reversible boundary work. For processes that are internally (or completely) reversible, the area under the process curve represents heat transfer. The term "irreversible processes" has no meaning in this context. Equations 1 and 2 can also be expressed in terms of unit mass as
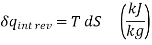
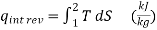…….3,4
To carry out the integrations in Equations 2 and 4, one must first understand the relationship between T and s during a process. The internally reversible isothermal process is one example of a special case in which these integrations are simple. It produces
(kJ)
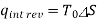(kJ/kg)
5 or 6, where T0 is the constant temperature and S is the system's entropy change during the process. On a T-s diagram, an isentropic process is easily identified as a vertical line segment. This is to be expected because an isentropic process does not involve heat transfer, so the area under the process path must be zero.
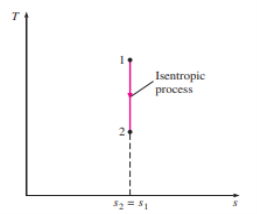
The isentropic process appears as a vertical line segment on a T-s diagram.
T-s diagrams are useful tools for visualising the second-law aspects of processes and cycles and are thus widely used in thermodynamics. The water T-s diagram is shown in the appendix in Fig. A–9. The enthalpy-entropy diagram is another common engineering diagram that is useful in the analysis of steady-flow devices such as turbines, compressors, and nozzles.
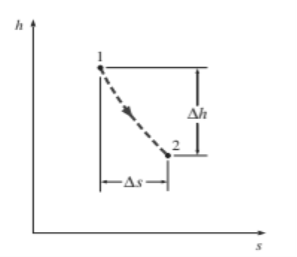
For adiabatic steady-flow devices
The vertical distance h on an h-s diagram represents work, and the horizontal distance s represents irreversibility.
The coordinates of an h-s diagram represent two important properties: enthalpy, which is a primary property in the first-law analysis of steady-flow devices, and entropy, which accounts for irreversibility during adiabatic processes. In analysing the steady flow of steam through an adiabatic turbine, for example, the vertical distance h between the inlet and exit states is a measure of the turbine's work output, and the horizontal distance s is a measure of the process's irreversibility (Fig. 7–18). The h-s diagram is also called a Mollier diagram.
TEMPERATURE-ENTROPY DIAGRAM:
Entropy may also be defined as the thermal property of a substance which remains constant when substance is expanded or compressed adiabatically in a cylinder.
ENTROPY CHANGES FOR A CLOSED SYSTEM:
General Case for Change of Entropy of a Gas
Let 1 kg of gas at a pressure p1, volume v1, absolute temperature T1 and entropy s1, be heated such that its final pressure, volume, absolute temperature and entropy are p2, v2, T2 and s2 respectively.
Then by law of conservation of energy,
Now,
Dividing both sides by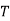 
, we get
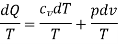
But
and as
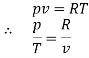
Hence
Integrating both sides, we get
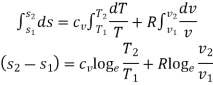
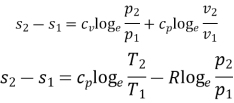
Heating a Gas at Constant Volume
Let 1 kg of gas be heated at constant volume and let the change in entropy and absolute temperature be from s1 to s2 and T1 to T2 respectively.
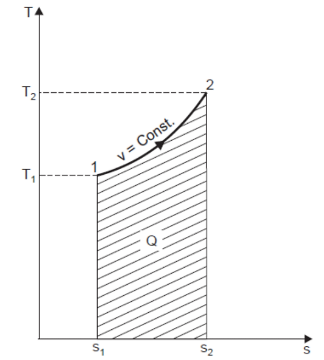
Then, Q= Cv (T2 - T1)
Differentiating to find small increment of heat dQ corresponding to small rise in temperature dT.
DQ = Cv dT
Dividing both sides by T, we get,
DQ / T = Cv dT / T
DS= Cv dT / T
Integrating both the sides, we get,
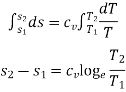
Heating a Gas at Constant Pressure
Let 1 kg of gas be heated at constant pressure and let the change in entropy and absolute temperature be from s1 to s2 and T1 to T2 respectively.
Then, Q= Cp (T2 - T1)
Differentiating to find small increase in heat, dQ of this gas when the temperature rise is dT.
DQ = Cv dT
Dividing both sides by T, we get,
DQ / T = Cv dT / T
DS= Cv dT / T
Integrating both the sides, we get,
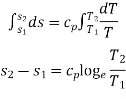
Isothermal Process
Entropy changes from s1 to s2 when gas absorbs heat during expansion. The heat taken by the gas is given by the area under the line 1-2 which also represents the work done during expansion. In other words, Q = W.
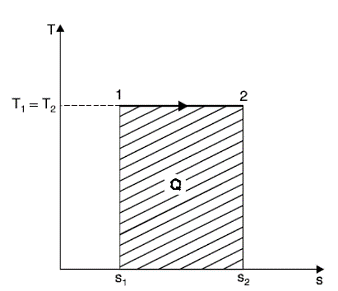
But,
Q= T (s2 - s1)
W = p1v1 loge (v2 / v1)
=RT1 loge (v2 / v1)
Hence,
T (s2 - s1) = RT1 loge (v2 / v1)
(s2 - s1) = R loge (v2 / v1)
Adiabatic Process (Reversible)
During an adiabatic process, heat is neither rejected nor absorbed by the system.
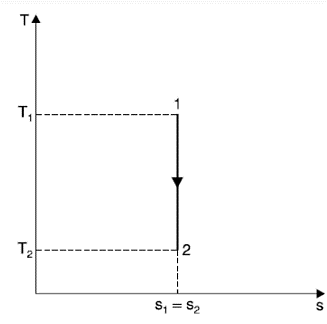
DQ = 0
DS = 0
Summary of formulae
S. No | Process | Change of entropy (per kg) |
1. | General case | (i) 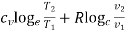 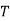 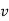 (ii)  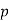 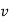 (iii)    |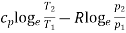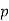
2. | Constant volume |  |
3. | Constant pressure |  |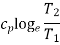
4. | Isothermal |  |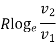
5. | Adiabatic | Zero |
6. | Polytropic | 
|
According to thermodynamics sources of energy is Classified as High grade & Low-grade energy.
High Grade | Low Grade |
Mechanical Work | Heat or Thermal energy |
Electrical energy | Nuclear fission or fusion |
Water power | Fossil fuels |
Wind power |
|
Kinetic energy of a Jet |
|
Tidal Power |
|
Low grade energy cannot be completely converted into high grade energy by 2nd law of thermodynamics. The part of energy which is left after conversion is known as Available energy.
That rejected energy is called as Unavailable energy.
Key Takeaway:
- The part of energy which is left after conversion is known as Available energy.
- That rejected energy is called as Unavailable energy
Availability:
Availability is defined as the Max useful work which can be obtained during a process in which the system comes in equilibrium with its surroundings.
| Initial Values | Final Values |
Internal Energy | U | U0 |
Entropy | S | S0 |
Volume | V | V0 |
Note:
The heat of the system is being exchanged with the environment, it may be both reversible and irreversible.
Useful work is given by,
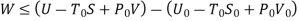
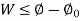
Where,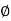 
is availability function, i.e., a composite function of both
System and environment.
Thus, the useful work is ≤ the decrease in the availability function.
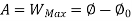
A= Availability
This work is obtained from a decrease in the internal energy of system & heat removed from environment.
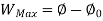
A system has two equilibrium states then,
Availability in steady flow:
A mass m is flowing in the system then,
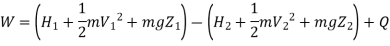
Assuming KE & PE are negligible
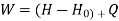
Entropy at entrance & exit = S & 
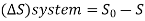
From entropy,
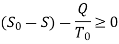
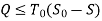
Useful work,
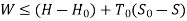
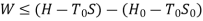
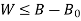
B is called availability function for steady state flow also known as Keenan Function.
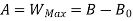
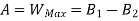
The availability & Unavailable quantity 
are also called Energy & Anergy respectively.
Irreversibility:
The work done in idealized Process is always more than actual Process. The difference between these two is called irreversibility (Degradation or Dissipation).
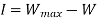
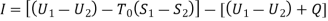
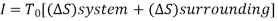
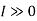
Irreversibility in steady flow:
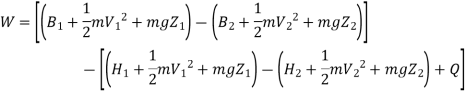
The same expression for irreversibility applies to both flow and non-flow process.
Key Takeaway:
According to 2nd law of thermodynamics, complete conversion of absorbed heat energy into equivalent amount of work is impossible.
Let us assume energy Q as heat, received from a body having temperature T.
The work done would be maximum if the engine operates on Carnot Cycle. The body at temperature T as source and the atmospheric temperature T0 as the sink.
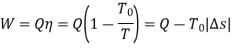
Where Ds is the change in entropy of the body
The Carnot cycle and the available energy is shown in figure.
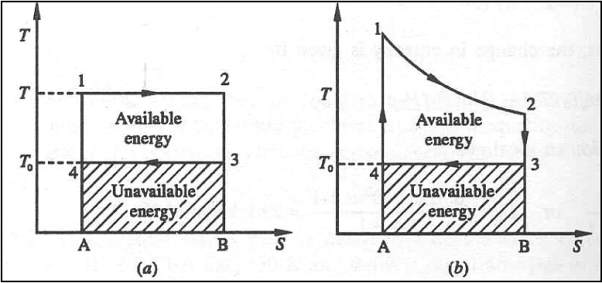
The area 1-2-3-4 represents the amount of energy available for utilization. The shaded are represents unavailable energy.
Availability Function for Non-Flow process:
If P0 is atmospheric pressure, V1 and V0 are the initial and final volumes of the system respectively.
If the system comes to equilibrium with its surroundings, the work done in against the atmospheric pressure is P0(V0-V1).
Availability = Wuseful = Wmax - P0(V0-V1)
Wmax=(U1-U0) - T0 (S1-S0)
Availability = Wuseful = Wmax-P0(V0-V1)
= (U1 - T0 S1)- (U0 - T0 S0)- P0(V0-V1)
= (U1 + P0V1 - T0 S1) - (U0 + P0V0 - T0 S0)
= f1-f0
Where, f = U+P0V-T0S is availability function for the non-flow process. Thus, the availability: f1 - f0
Availability Function for Steady Flow process:
The maximum work that can be done in a SF process while the control volume exchanges heat with the atmosphere at T0, is given by:
It can also be expressed as
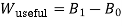where,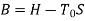 
Which is called the Darrieus Function.
When a fluid flows through a control volume, its thermodynamic properties can change along space coordinates as well as over time. If the rates of flow of mass and energy through the control surface change over time, so will the mass and energy within the control volume.
The term' steady flow' refers to the constant rates of mass and energy flow across the control surface.
At the steady state of a system, any thermodynamic property has a fixed value at a specific location and does not change over time.
Thermodynamic properties vary along space coordinates but not with time. The term' steady state' refers to a state that is constant or invariant over time.
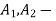cross-section of stream,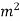 
mass flow rate, kg/s
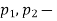pressure, absolute N/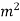
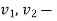specific volume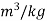 
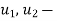specific internal energy,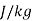 
velocity m/s
elevation above an arbitrary datum, m
DQ/dt – net rate of heat transfer through the control surface, J/s
netrate of work transfer through the control surface, J/s
Exclusive of work done at sections 1 and 2 in transferring the fluid through the control surface .
- time, s.
Mass Balance
According to the law of conservation of mass, if no mass accumulates within the control volume, the mass flow rate entering must equal the mass flow rate leaving.
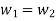
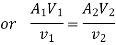
This is referred to as the equation of continuity.
Key Takeaway:
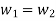
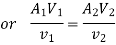
Work transfer in a flow process can be of two types: external work and flow work. The term "external work" refers to all work transfer across the control surface that is not caused by normal fluid forces. Shear (shaft or stirring) work and electrical work are the only types of external work that matter in engineering thermodynamics. Only external work, Wx, takes the form of shaft work. The flow work is the displacement work done by a fluid of mass dm1 at the inlet section I and a fluid of mass d2 at the exit section 2, which are (-p1 v1dm1) and (+p2v2dmi) respectively. As a result, total work transfer is given by
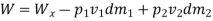
In the rate form,
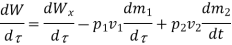
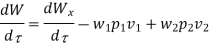
Because there is no energy accumulation, the total rate of flow of all energy streams entering the control volume must equal the total rate of flow of all energy streams leaving the control volume. This can be expressed mathematically as follows.
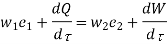
Substituting for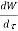 
from eq 5.4
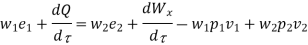
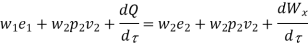
Where e1 and e2 denote the energy carried into or out of the control volume per unit mass of fluid.
The specific energy e is given by
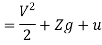
Substituting the expression for e in 5.5
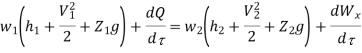
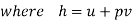
And since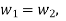 
let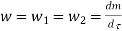 
Dividing by dm/d
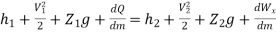
Or it can also be written as
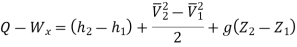
In differential form it is written as
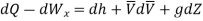
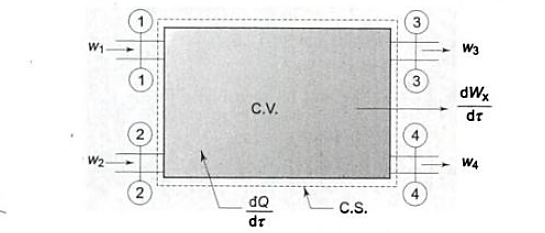
Mass balance
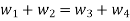
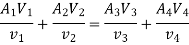
Energy balance
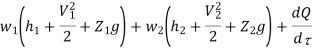
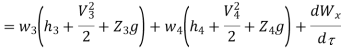
References:
- Basic and Applied Thermodynamics by PK Nag, MCGRAW HILL INDIA.
- Thermodynamics for Engineers by Kroos& Potter, Cengage Learning.
- Thermodynamics by Shavit and Gutfinger, CRC Press.
- Thermodynamics- An Engineering Approach by Cengel, MCGRAW HILL INDIA.
- Basic Engineering Thermodynamics, Joel, Pearson.
