Unit - 6
Mass Transfer
Introduction
- Heat is transferred if there is a temperature difference in a medium. Similarly, if there is a difference in the concentration of some chemical species in a mixture, mass transfer must occur.
- A species is an identifiable molecule, such as carbon dioxide, CO2, that can be transported by diffusion and/or converted to some other form by a chemical reaction. A species may be a single atom or a complex polyatomic molecule. It can also be appropriate to identify a mixture (such as air) as a species.
- Mass transfer is mass in transit as the result of a species concentration difference in a mixture.
- Just as a temperature gradient constitutes the driving potential for heat transfer, a species concentration gradient in a mixture provides the driving potential for transport of that species.
- The bulk flow of fluid due to pressure gradient occurring at a macroscopic level is a kind of mass transfer usually treated in the subject of fluid mechanics.
- For example, the term mass transfer is not used to describe the motion of air that is induced by a fan or the motion of water being forced through a tube. In both cases, there is gross or bulk fluid motion due to mechanical work.
- We are concerned with mass transfer occurring at a microscopic or molecular level, which deals with the transport of one constituent of a fluid solution or gas mixture from a region of higher concentration to a region of lower concentration.
- Drying, evaporation, chemical reaction, absorption, adsorption, solution and so on are all instances of mass transfer.
Physical origins
- Consider a chamber in which two different gas species at the same temperature and pressure are initially separated by a partition. If the partition is removed without disturbing the fluid, both species will be transported by diffusion. Figure 6.1 shows the situation as it might exist shortly after removal of the partition.
- A higher concentration means more molecules per unit volume, and the concentration of species A (light dots) decreases with increasing x, while the concentration of B increases with x.
- Since mass diffusion is in the direction of decreasing concentration, there is net transport of species A to the right and of species B to the left.
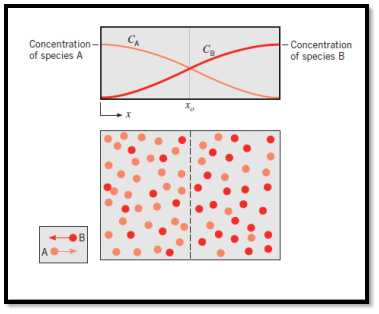
Fig 1 Mass transfer by diffusion
- The physical mechanism may be explained by considering the imaginary plane shown as a dashed line at xo. Since molecular motion is random, there is equal probability of any molecule moving to the left or the right. Accordingly, more molecules of species A cross the plane from the left, since this is the side of higher A concentration than from the right. Similarly, the concentration of B molecules is higher to the right of the plane than to the left, and random motion provides for nettransfer of species B to the left. After a sufficient time, uniform concentrations of A and B are achieved, and there is no nettransport of species A or B across the imaginary plane.
- Mass diffusion occurs in liquids and solids, as well as in gases. However, since mass transfer is strongly influenced by molecular spacing, diffusion occurs more readily in gases than in liquids and more readily in liquids than in solids.
Mass transfer by molecular diffusion is analogous to heat transfer by conduction or momentum transfer in laminar flow. Mass transfer by molecular diffusion may occur in a stagnant fluid or in a fluid in laminar flow. Like the Fourier’s equation of heat conduction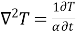
, the concentration field of the diffusing species A is given by
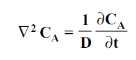
Where CA is the concentration of component A in a mixture of A and B in kgmol/m3, t is the time in seconds and D is the mass diffusivity in m2/s.
For one-dimensional mass diffusion,
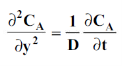
Wherey is the distance in the direction of diffusion.
Like the conduction equation
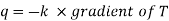
The mass transfer equation is
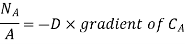
For one dimensional mass transfer
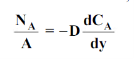…(6.1)
Where NA/A is the mass flux in kgmol/m2s. The negative sign appears because the concentration gradient is negative in the direction of mass transfer.
Equation (6.1) is called Fick’s law of diffusion, which states that the mass flux of a constituent per unit area is proportional to the concentration gradient.
In Fig. 6.2 a thin partition separates the two gases A and B. When the partition is removed, the two gases diffuse through each other until equilibrium is established and the concentration of the gases is uniform throughout the box. The diffusion rate is given by Eq. (6.1). It can also be expressed in terms of mass flow:
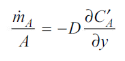…(6.2)
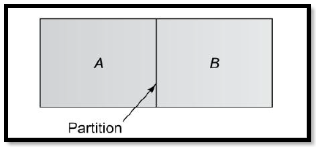
Fig. 2 Diffusion of component A into component B and vice versa
Where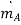
is the mass flux per unit time, kg/s; CA is the mass concentration of component A per unit volume, kg/m3; and D is the proportionality constant called diffusion coefficient, m2/s.
Equimolar diffusion
In the gas phase, the concentrations are usually expressed in terms of partial pressures. If ideal gas law is assumed to hold good.
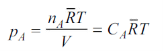
Where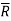
is the universal gas constant.
Fick’s law could then be written as
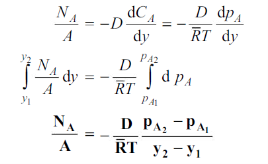…(6.3)
WherepA1 is the partial pressure of A at y1 and pA2 is the partial pressure of A at y2.
Equation (6.3) is valid for equimolar counter diffusion in which gases A and B diffuse simultaneously in opposite directions through each other. The rates of diffusion are equal but in opposite direction i.e., NA = – NB.
And also
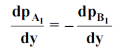
Molecular diffusion through stationary gas
Let us consider a gas Adiffusing through a stationary gas B into a liquid–vapour interface where the gas A is absorbed. Since the gas A is diffusing towards the interface, there must be a partial pressure gradient for A in the direction of diffusion.
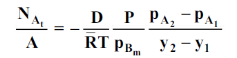
Where 
and 
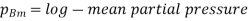which is
Diffusivity For Gases and Vapours
Gilliland proposed a semi-empirical equation for the diffusion coefficient in gases.
…(6.4)
Where D is in cm2/s, T is in K, p is the total system pressure in pascals and VA and VB are the molecular volumes of constituents A and B as calculated from the atomic volumes; MAand MBare the molecular weights of constituents A and B.
Concentration boundary layer and mass transfer coefficient
Just as the calculation of momentum and heat transfer requires the knowledge of velocity and temperature profiles within the boundary layer, the calculation of mass transfer requires that concentration profile within the boundary layer should be known.
Fig 3 Concentration boundary layer
Let us consider the flow of a fluid mixture on a surface as shown in figure. Let the free stream velocity and concentration be 
and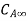 
. Let the plate surface be maintained at a concentration 
>
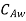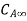. Then, species A diffuses from the surface into the fluid. A concentration boundary layer develops , thickness of which can be defined in the same way as that of the hydrodynamic o thermal boundary layer. The distance 
to which the boundary layer extends may be defined as the thickness at which the concentration is equal to 99% of the free-stream concentration
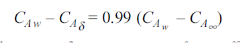
By analogy of heat transfer, mass transfer coefficient hm can be defined as
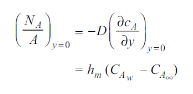
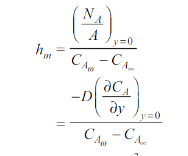…(6.5)
Unit of hm is same as velocity i.e m/s.
The molecular diffusion equation is
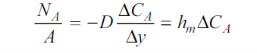
For gas
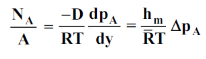
Analogy Between Momentum, Heat and Mass Transfer
The momentum and energy equations of a laminar boundary layer are
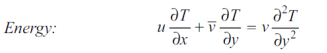
The concentration boundary layer can similarly be simplified to
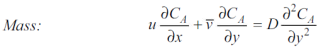
Momentum transfer in laminar flow (Newton’s law) is
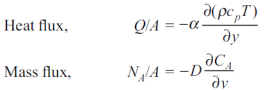
We know that the velocity and temperature profiles have the same shape if
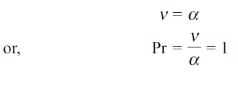
Similarly, the momentum and concentration profiles will have the same shape if
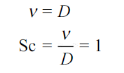
Where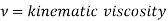 
Thus, the Schmidt number plays the same role in mass transfer as does the Prandtl number in heat transfer.
It is also seen that the temperature and concentration profiles will be similar if
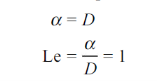
Where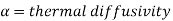 
Thus, Lewis number is important in the solution of simultaneous heat and mass transfer problems. When,
Sc = Pr = Le = 1, all the three boundary layers coincide.
The dimensionless mass transfer number corresponding to the Nusselt number is the Sherwood number defined as
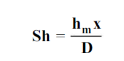...(6.6)
Wherex is the characteristic length.
Similarly, corresponding to Stanton number, which is expressed as
Corresponding to it, we have
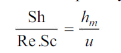
Whereu is any characteristic velocity of the system.
We know that forced convection heat transfer correlations are of the form
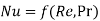
Likewise, in forced convection mass transfer problems we write the functional relation
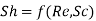
Heat transfer and Mass transfer are similar very similar to one another. Similarities between them can be explained by following key points.
- Heat transfer takes place by the virtue of temperature difference. Similarly, mass transfer takes place because of concentration difference between two points.
- Heat flows from high temperature to low temperature. Whereas, mass transfer takes place from high concentration to low concentration.
- Heat transfer by conduction is explained with the help of Fourier’s law which is given as
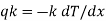
Where, qkis the rate of heat flux (a vector) in W/m2, dT/dx is the temperature gradient in the direction of heat flow x and k is the constant of proportionality
Mass transfer is explained with help of Fick’s law which is given as
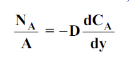
Where NA/A is the mass flux,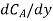 
is concentration gradient and D is constant of proportionality.
- Heat convection takes place by molecular diffusion whereas, mass convection takes place by mass diffusion.
- Heat convection equation is gives as
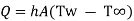
Where, Q is rate of heat transfer (W), A is area in m2, h is constant known as coefficient of convective heat transfer or film coefficient with unit W/m2K.
Mass convection equation is given as
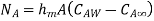
Where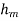 
is coefficient of mass convection, 
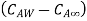represent concentration difference.
- Nusselt number, Reynold,s number and Prandtl number are governing constants of heat convection. They can be correlated as
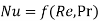
Likewise, Sherwood number, Reynold’s number and Schmidt number are governing constants in convection mass transfer which can be correlated as
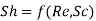
Important Formulae
Mass flux |  |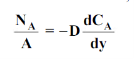
Equimolar diffusion |  |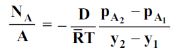
Diffusivity of gas and vapour |  |
Mass flux by convection |  |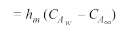
Sherwood’s number |  |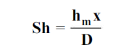
References:
- Bejan, Heat Transfer John Wiley, 1993
- J.P. Holman, Heat Transfer, Eighth Edition, McGraw Hill, 1997.
- F.P. Incropera, and D.P. Dewitt, Fundamentals of Heat and Mass Transfer, John Wiley, Sixth Edition, 2007.
- Massoud Kaviany, Principles of Heat Transfer, John Wiley, 2002
- Yunus A Cengel, Heat Transfer: A Practical Approach, McGraw Hill, 2002
