UNIT – I
Ratio and proportion
Ratio-
The ratio of two quantities ‘x’ and ‘y’ of same kind is obtained by dividing x by y and it is denoted by x : y
The first term is called antecedent and the second term is called consequent.
Example: 2/3 or 2:3
Example: Divide 500 into two people A and B ratio 2:3.
Sol.
Here sum of the ratio is = 2 + 3 = 5
Then,
A’s share = 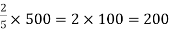
B’s share = 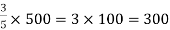
Continued ratio-
A ratio is said to be in continued if consequent of one ratio is antecedent of the other.
For example- a:b and b:c is in continued ratio.
Example: If Rs. 74000 are to be divided among three people X, Y and Z such that
X : Y = 4 : 5 and Y : Z = 3 : 2 then what amount each person will recieve?
Sol.
Here X:Y:Z: = 12:15:10
Here sum of the ratio is = 12 + 15 + 10 = 37
Then-
X will get = 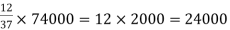
Y will get = 
Z will get = 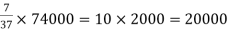
Inverse ratio-
For the ratio x : y, the inverted ratio will be y:x.
Example: inverse ratio of 3:4 is 4:3
Note-
A ratio remains same if it is multiplied or divided by the same number.
X: y = mx : my ( multiplied by ‘m’)
X:y = x/m:y/m (divided by m)
Example:
4:5 = 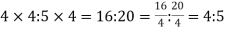
Proportion-
Proportion is an equation that equates two ratios in same proportion,
If the ratio a/b is equals to the ratio c/d then the following proportion can be written-
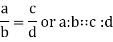
Here a and d are called the extremes of the proportion, the numbers b and c are called means of the proportion
Properties of proportion-
- Cross product property: The product of the extremes equals the product of the means.
If 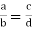 then ad = bc
then ad = bc
2. Reciprocal property: If two ratios are equal, then their reciprocals are also equal.
If 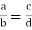 then If
then If 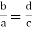 .
.
Continued proportion-
The quantities p, q, r, s, t..... are said to be in continued proportion of p:q = q:r = r:s.....
Example: If 2, x and 32 are in continued proportion then find the value of x.
Sol.
Here it can be written as-
2 : x = x:32
Or
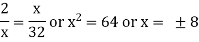
Note- if a, b, c are in continued proportion then 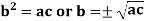
Fourth, third and mean proportional-
If p:q = r:s then-
- S is called the fourth proportional to p,q,r.
- R is called the third proportion to p and q.
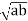 is called the mean proportional between a and b.
is called the mean proportional between a and b.
Compound proportion-
If two or more ratios are multiplied together then they are known as compounded.
Thus a1 a2 a3 : b1 b2 b3 is a compounded ratios of the ratios a1 : b1 ; a2 : b2 and a3 : b3. This method is also known as compound rule of three.
Example: 10 men working 8 hours a day can finish a work in 12 days. In how many days can 12 men working 5 hours a day finish the same work?
Sol.
This can be arranged as-

Then

Important properties of proportion-
Given quantities a, b, c, d are in proportion.
- Invertendo: If a : b = c : d then b : a = d : c
- Alternendo : If a : b = c : d, then a : c = b : d
- Componendo and Dividendo- if
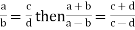
Note-
- If x : y = a : b, it does not mean x = a, y = b. It is however to take x = ka, y = kb
- if
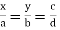 is sometimes written as x : y : z = a : b : c.
is sometimes written as x : y : z = a : b : c.
Example: The marks obtained by four examinees are as follows: A : B = 2 : 3, B : C = 4 : 5, C : D = 7 : 9, find the continued ratio.
Sol.
A : B = 2 : 3
B : C = 4 : 5 = 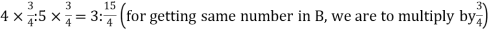
C : D = 7 : 9 =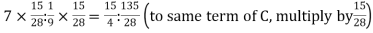
A : B : C : D = 2 : 3 :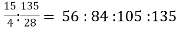
Example: Two numbers are in the ratio of 3 : 5 and if 10 be subtracted from each of them, the remainders are in the ratio of 1 : 5, find the numbers.
Sol.
Let the numbers be x and y, so that- x/y =3/5 or 5x = 3y … (1)
Again-
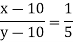
Or
5x – y = 40… (2)
By solving (1) and(2), we get-
X = 12 and y = 20
Hence the required numbers are- 12 and 20
Example: The prime cost of an article was three times the value of material used. The cost of raw materials was increased in the ratio 3 : 4 and the productive wage was increased in the ratio 4 : 5. Find the present prime cost of an article, which could formerly be made for Rs.180.
Sol.
Prime cost = x + y, where x = productive wage, y = material used
Now prime cost = 180 =3y or, y = 60, again x + y = 180, x = 180–y = 180–60 = 120
Present material cost = 4y/3 and present wage = 5x / 4
Present prime cost–
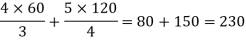
Hence the present prime cost is Rs. 230.
Direct and inverse proportion-
Direct proportion or direct variation-
Direct proportion or direct variation is the relation between two quantities where the ratio of the two is equal to a constant value. It is represented by the proportional symbol, ∝
Or we can say that two values said to be in direct proportion when one variable increases then other value also increases.
If we have two quantities ‘a’ and ‘b’ which are lined with each other directly then we can say- a ∝ b
When we remove proportionality sign, the ratio of ‘a’ and ‘b’ becomes equals to a constant.
a = Cb
For example: if the number of individuals visiting a restaurant increases, earning of the restaurant also increases.
Inverse proportion-
Inverse proportion is when one value increases and the other value decreases.
For example- We need more manpower to reduce the time to complete a task. They are inversely proportional.
Questions based on direct and inverse proportion-
Example: A machine in a drinking water supplying factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
Sol.
Let the bottles filled by machine in 5 hours be x
We can write the given information as follows-
Number of bottles | Tine taken (in hrs) |
840 | 6 |
X | 5 |
There is a direct relationship between time taken and bottles filled by machine,
So that, we get-
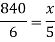

So that 700 bottles can be filled by the machine in 5 hrs.
Example: In a model of a ship, the mast is 9 m high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?
Sol.
Suppose the mast of the model ship be x, then
We can write the given information as follows-
| Height of mast | Length of ship |
Model ship | 9 m | x |
Actual ship | 12m | 28m |
There is a direct relationship-
So that,
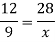
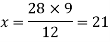
So that the length of a model ship is 21m.
Example: 10 men can do a piece of work in 30 days then in how many days 20 men can do the same work?
Sol.
Let ‘x’ days be taken to do the task,
Then
Men | Days |
10 | 30 |
20 | X |
There is inverse relationship, so that-
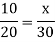

So that 20 men can do the same piece of work in 15 days.
Key takeaways-
- The ratio of two quantities ‘x’ and ‘y’ of same kind is obtained by dividing x by y and it is denoted by x:y
- The first term is called antecedent and the second term is called consequent.
- A ratio is said to be in continued if consequent of one ratio is antecedent of the other.
- For the ratio x:y, the inverted ratio will be y:x.
- A ratio remains same if it is multiplied or divided by the same number.
- Proportion is an equation that equates two ratios in same proportion

- If
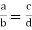 then ad = bc
then ad = bc - If
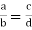 then If
then If 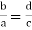
- If two or more ratios are multiplied together then they are known as compounded.
- When we remove proportionality sign, the ratio of ‘a’ and ‘b’ becomes equals to a constant.
a = Cb
12. Inverse proportion is when one value increases and the other value decreases.
1.2 Logarithms
A logarithm is the power to which a number must be raised in order to get some other number. For example, the base ten logarithm of 100 is 2, because ten raised to the power of two is 100:
log 100 = 2
because
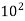 = 100
= 100
This is an example of a base-ten logarithm. We call it a base ten logarithm because ten is the number that is raised to a power. The base unit is the number being raised to a power. There are logarithms using different base units. If you wanted, you could use two as a base unit. For instance, the base two logarithm of eight is three, because two raised to the power of three equals eight:
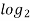 8 = 3
8 = 3
because
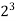 = 8
= 8
In general, you write log followed by the base number as a subscript. The most common logarithms are base 10 logarithms and natural logarithms; they have special notations. A base ten log is written
log
and a base ten logarithmic equation is usually written in the form:
log a = r
A natural logarithm is written
ln
and a natural logarithmic equation is usually written in the form:
ln a = r
So, when you see log by itself, it means base ten log. When you see ln, it means natural logarithm (we'll define natural logarithms below). In this course only base ten and natural logarithms will be used.
Properties of Logarithms
-
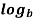 mn =
mn = 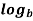 m +
m +  n
n 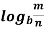 =
= 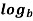 m -
m - 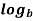 n
n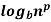 = p
= p 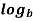 n
n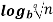 =
= 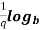 n
n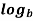 n =
n =  n
n 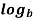 a
a- Zero Exponent Rule:
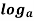 1 = 0
1 = 0
1. Express 53 = 125 in logarithm form.
Solution:
53 = 125
As we know,
ab = c ⇒ logac=b
Therefore;
Log5125 = 3
2. Express log101 = 0 in exponential form.
Solution:
Given, log101 = 0
By the rule, we know;
logac=b ⇒ ab = c
Hence,
100 = 1
3. Find the log of 32 to the base 4.
Solution: log432 = x
4x = 32
(22)x = 2x2x2x2x2
22x = 25
2x=5
x=5/2
Therefore,
log432 =5/2
4. Find x if log5(x-7)=1.
Solution: Given,
log5(x-7)=1
Using logarithm rules, we can write;
51 = x-7
5 = x-7
x=5+7
x=12
5. If logam=n, express an-1 in terms of a and m.
Solution:
logam=n
an=m
an/a=m/a
an-1=m/a
6. Solve for x if log(x-1) +log(x+1) =log21
Solution: log(x-1) +log(x+1) =log21
log(x-1) +log(x+1) =0
log[(x-1) (x+1)] =0
Since, log 1 = 0
(x-1) (x+1) = 1
x2-1=1
x2=2
x=± √2
Since, log of negative number is not defined.
Therefore, x=√2
7. Express log (75/16)-2log (5/9) +log (32/243) in terms of log 2 and log 3.
Solution: log (75/16)-2log (5/9) +log (32/243)
Since, nlogam=logamn
⇒log (75/16)-log (5/9)2+log (32/243)
⇒log (75/16)-log (25/81) +log (32/243)
Since, logam-logan=loga(m/n)
⇒log [(75/16) ÷ (25/81)] +log (32/243)
⇒log [(75/16) × (81/25)] +log (32/243)
⇒log (243/16) +log (32/243)
Since, logam+logan=logamn
⇒log (32/16)
⇒log2
8. Express 2logx+3logy=log a in logarithm free form.
Solution: 2logx+3logy=log a
logx2+logy3=log a
logx2y3=log a
x2y3=log a
9. Prove that: 2log (15/18)-log (25/162) +log (4/9) =log2
Solution: 2log (15/18)-log (25/162) +log (4/9) =log2
Taking L.H.S.:
⇒2log (15/18)-log (25/162) +log (4/9)
⇒log (15/18)2-log (25/162) +log (4/9)
⇒log (225/324)-log (25/162) +log (4/9)
⇒log [(225/324) (4/9)]-log (25/162)
⇒log [(225/324) (4/9)]/ (25/162)
⇒log (72/36)
⇒log2 (R.H.S)
10. Express log10(2+1) in the form of log10x.
Solution: log10(2+1)
=log102+log101
=log10(2×10)
=log1020
11. Find the value of x, if log10(x-10) =1.
Solution: Given, log10(x-10) =1.
log10(x-10) = log1010
x-10 = 10
x=10+10
x=20
12. Find the value of x, if log(x+5) +log(x-5) =4log2+2log3
Solution: Given,
log(x+5) +log(x-5) =4log2+2log3
log(x+5) (x-5) = 4log2+2log3 [log mn=log m+log n]
log(x2-25) = log24+log32
log(x2-25) = log16+log9
log(x2-25) =log (16×9)
log(x2-25) =log144
x2-25=144
x2=169
x=±√169
x=±13
13. Solve for x, if log(225/log15) = log x
Solution: log x = log(225/log15)
log x=log [(15×15)]/log15
log x = log 152/log 15
log x = 2log 15/log 15
log x = 2
Or
log10x=2
102=x
x=10×10
x=100
Anti-Logarithms (Antilog)
The anti-logarithm of a number is the inverse process of finding the logarithms of the same number. If x is the logarithm of a number y with a given base b, then y is the anti-logarithm of (antilog) of x to the base b.
|
Natural Logarithms and Anti-Logarithms have their base as 2.7183. The Logarithms and Anti-Logarithms with base 10 can be converted into natural Logarithms and Anti-Logarithms by multiplying it by 2.303.
Anti-Logarithmic Table
To find the anti-logarithm of a number we use an anti-logarithmic table. Below are the steps to find the antilog.
- The first step is to separate the characteristic and the mantissa part of the number.
- Use the antilog table to find a corresponding value for the mantissa. The first two digits of the mantissa work as the row number and the third digit is equal to the column number. Note this value.
- The antilog table also includes columns which provide the mean difference. For the same row of the mantissa, the column number in the mean difference is equal to the fourth digit. Note this value.
- Add the values so obtained.
- In the characteristic add one. This value shows the place to put the decimal point. The decimal point is inserted after that many digits from the left.
Solved Examples on Logarithms and Anti-Logarithms
- Problem: Find the value of log 2.8726.
Solution: Here the number of digit to the left of the decimal is 1 so the value of the characteristic will be one less than one i.e., 0.
From the log table, the value of 2.8726 is 0.45827. Adding the values of mantissa and the characteristic we find the value of the logarithm.
So, log 2.8725 = 0 + 0.45827 = 0.45827.
2. Problem: Calculate the antilog of 3.6552.
Solution: Here we need to find the number whose logarithm is 3.655. From the antilog table, the value corresponding to the row 65 and column 5 is 4508.
The mean difference column for the value 2 is 2. Adding these two values, we have 4518 + 2 = 4520.
The decimal point is placed in 3 + 1 = 4 digits from the left. So, antilog 3.6552 = 4520.0
3. If log x = -2.0258, find x.
Solution:
In order to find the value of x using antilog-table, the decimal part (i.e., the mantissa) must be made positive. For this we proceed as follows:
log x = -2.0258 = - 3 + 3 - 2.0258
= - 3 + .9742 =3.9742
Therefore, x = antilog 3.9742.
Now, from antilog table we get the number corresponding to the mantissa
.9742 as (9419 + 4) = 9423.
Again the characteristic in log x is (- 3).
Hence, there should be two zeroes between the decimal point and the first significant digit in the value of x.
Therefore, x = .009423.
Key Takeaways:
- A logarithm is the power to which a number must be raised in order to get some other number.
- The anti-logarithm of a number is the inverse process of finding the logarithms of the same number. If x is the logarithm of a number y with a given base b, then y is the anti-logarithm of (antilog) of x to the base b.
1.3 Percentage
Percent means a part per 100. A percentage is a number that can be expressed as fraction of 100.
We use the symbol % for percentage.
We can represent percentage in decimal or fraction form.
We use the following formula to calculate percentage-
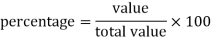
For example: if a student got 300 marks out of 500 then his result in percentage will be-
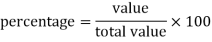
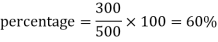
Percentage Increase and Decrease
The percentage increase is equal to the subtraction of original number from a new number, divided by the original number and multiplied by 100.
% increase = [(New number – Original number)/Original number] x 100
where, increase in number = New number – original number
% decrease = [(Original number – New number)/Original number] x 100
Where decrease in number = Original number – New number
Example: Find 70 % of 30
Sol.
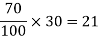
Example: A person has a monthly salary of Rs. 20,000. He spends 8000 per month on food then what percent of his monthly salary does he save?
Sol.
Person’s monthly salary = 20,000
Savings = (20,000 – 8000) = 12,000
Fraction of his saving = 12,000/20,000
By converting the fraction into percentage, we get-
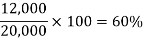
Example: A shopkeeper reduced the price of an item by 25%, the old price was 120 then find out the new price.
Sol.
25% of 120 will be-
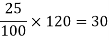
Which means he reduced Rs. 30, then the new price is-
120 – 30 = 90
The new price is Rs. 90
Example: If 20% of any number is 500 then find out the number?
Sol.
Let the number is ‘x’, then-
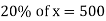
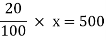

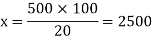
Hence the number is 2500.
decrease in number = Original number – New number
Key takeaways-
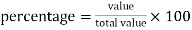
- % increase = [(New number – Original number)/Original number] x 100
- % decrease = [(Original number – New number)/Original number] x 100
- decrease in number = Original number – New number
1.4 Average
Mean
- The mean is the arithmetic average, also called as arithmetic mean.
- Mean is very simple to calculate and is most commonly used measure of the center of data.
- Means is calculated by adding up all the values and divided by the number of observation.
Computation of sample mean -
If X1, X2, ………………Xn are data values then arithmetic mean is given by
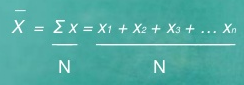
Computation of the mean for ungrouped data
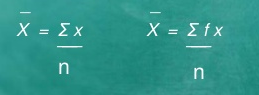
Example 1 – The marks obtained in 10 class test are 25, 10, 15, 30, 35

 The mean = X = 25+10+15+30+35 = 115 =23
The mean = X = 25+10+15+30+35 = 115 =23
5 5
Analysis – The average performance of 5 students is 23. The implication is that students who got below 23 did not perform well. The students who got above 23 performed well in exam.
Example 2 – Find the mean
Xi | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Freq (Fi) | 2 | 5 | 12 | 17 | 14 | 6 | 3 |
Xi | Freq (Fi) | XiFi |
9 | 2 | 18 |
10 | 5 | 50 |
11 | 12 | 132 |
12 | 17 | 204 |
13 | 14 | 182 |
14 | 6 | 84 |
15 | 3 | 45 |
| Fi = 59 | XiFi= 715 |
|
|
|
Then, N = ∑ fi = 59, and ∑fi Xi=715
 X = 715/59 = 12.11
X = 715/59 = 12.11
Mean for grouped data/ Weighted Arithmetic Mean
Grouped data are the data that are arranged in a frequency distribution
Frequency distribution is the arrangement of scores according to category of classes including the frequency.
Frequency is the number of observations falling in a category
The formula in solving the mean for grouped data is called midpoint method. The formula is
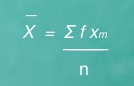
 Where, X = Mean
Where, X = Mean
Xm = midpoint of each class or category
f = frequency in each class or category
∑f Xm = summation of the product of fXm
Example 3 – the following data represent the income distribution of 100 families. Calculate mean income of 100 families?
Income | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
No. of families | 8 | 12 | 25 | 22 | 16 | 11 | 6 |
Solution:
Income | No. of families | Xm (Mid point) | fXm |
30-40 | 8 | 35 | 280 |
40-50 | 12 | 34 | 408 |
50-60 | 25 | 55 | 1375 |
60-70 | 22 | 65 | 1430 |
70-80 | 16 | 75 | 1200 |
80-90 | 11 | 85 | 935 |
90-100 | 6 | 95 | 570 |
| n = 100 |
| ∑f Xm = 6198 |

X = ∑f Xm/n = 6330/100 = 63.30
Mean = 63.30
Example 4 – Calculate the mean number of hours per week spent by each student in texting message.
Time per week | 0 - 5 | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 | 25 – 30 |
No. of students | 8 | 11 | 15 | 12 | 9 | 5 |
Solution:
Time per week (X) | No. of students (F) | Mid point X | XF |
0 - 5 | 8 | 2.5 | 20 |
5 – 10 | 11 | 7.5 | 82.5 |
10 - 15 | 15 | 12.5 | 187.5 |
15 - 20 | 12 | 17.5 | 210 |
20 - 25 | 9 | 22.5 | 202.5 |
25 – 30 | 5 | 27.5 | 137.5 |
| 60 |
| 840 |
Mean = 840/60 = 14
Example 5 –
The following table of grouped data represents the weights (in pounds) of all 100 babies born at a local hospital last year.
Weight (pounds) | Number of Babies |
[3−5) | 8 |
[5−7) | 25 |
[7−9) | 45 |
[9−11) | 18 |
[11−13) | 4 |
Solution:
Weight (pounds) | Number of Babies | Mid point X | XF |
[3−5) | 8 | 4 | 32 |
[5−7) | 25 | 6 | 150 |
[7−9) | 45 | 8 | 360 |
[9−11) | 18 | 10 | 180 |
[11−13) | 4 | 12 | 48 |
| 100 |
| 770 |
Mean = 770/100 = 7.7
Geometric mean
Geometric mean is a type of mean or average, which indicates the central tendency of a set of numbers by using the product of their values.
Definition
The Geometric Mean (G.M) of a series containing n observations is the nth root of the product of the values.
For ungrouped data
 Geometric Mean, GM = Antilog ∑logxi
Geometric Mean, GM = Antilog ∑logxi
N
Example 1 – find the G.M of the values
X | Log X |
45 | 1.653 |
60 | 1.778 |
48 | 1.681 |
65 | 1.813 |
Total | 6.925 |
 GM = Antilog ∑logxi
GM = Antilog ∑logxi
N
= Antilog 6.925/4
= Antilog 1.73
= 53.82
For grouped data
 Geometric Mean, GM = Antilog ∑ f logxi
Geometric Mean, GM = Antilog ∑ f logxi
N
Example 2 – calculate the geometric mean
X | f |
60 – 80 | 22 |
80 – 100 | 38 |
100 – 120 | 45 |
120 – 140 | 35 |
|
|
Solution
X | f | Mid X | Log X | f log X |
60 – 80 | 22 | 70 | 1.845 | 40.59 |
80 – 100 | 38 | 90 | 1.954 | 74.25 |
100 – 120 | 45 | 110 | 2.041 | 91.85 |
120 – 140 | 35 | 130 | 2.114 | 73.99 |
Total | 140 |
|
| 280.68 |
 GM = Antilog ∑ f logxi
GM = Antilog ∑ f logxi
N
= antilog 280.68/140
= antilog 2.00
GM = 100
Example 3 – calculate geometric mean
class | frequency |
2-4 | 3 |
4-6 | 4 |
6-8 | 2 |
8-10 | 1 |
Solution
class | frequency | x | Log x | flogx |
2-4 | 3 | 3 | 1.0986 | 3.2958 |
4-6 | 4 | 5 | 1.2875 | 6.4378 |
6-8 | 2 | 7 | 0.5559 | 3.8918 |
8-10 | 1 | 9 | 0.2441 | 2.1972 |
| 10 |
|
| 15.8226 |
 GM = Antilog ∑ f logxi
GM = Antilog ∑ f logxi
N
= antilog 15.8226/10
= antilog 1.5823
GM = 4.866
Harmonic mean
Harmonic mean is quotient of “number of the given values” and “sum of the reciprocals of the given values
For ungrouped data
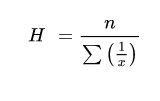
Example 1 - Calculate the harmonic mean of the numbers 13.2, 14.2, 14.8, 15.2 and 16.1
Solution
X | 1/X |
13.2 | 0.0758 |
14.2 | 0.0704 |
14.8 | 0.0676 |
15.2 | 0.0658 |
16.1 | 0.0621 |
Total | 0.3147 |
H.M of X = 5/0.3147 = 15.88
Example 2 - Find the harmonic mean of the following data {8, 9, 6, 11, 10, 5} ?
X | 1/X |
8 | 0.125 |
9 | 0.111 |
6 | 0.167 |
11 | 0.091 |
10 | 0.100 |
5 | 0.200 |
Total | 0.794 |
H.M of X = 6/0.794 = 7.560
For grouped data

Example 3 - Calculate the harmonic mean for the below data
Marks | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 |
F | 2 | 3 | 11 | 20 | 32 | 25 | 7 |
Solution
Marks | X | F | F/X |
30-39 | 34.5 | 2 | 0.0580 |
40-49 | 44.5 | 3 | 0.0674 |
50-59 | 54.4 | 11 | 0.2018 |
60-69 | 64.5 | 20 | 0.3101 |
70-79 | 74.5 | 32 | 0.4295 |
80-89 | 84.5 | 25 | 0.2959 |
90-99 | 94.5 | 7 | 0.0741 |
Total |
| 100 | 1.4368 |
HM = 100/1.4368 = 69.59
Example 4 – find the harmonic mean of the given class
Ages | 4 | 5 | 6 | 7 |
No. of students | 6 | 4 | 10 | 9 |
Solution
X | F | f/x |
4 | 6 | 1.50 |
5 | 4 | 0.80 |
6 | 10 | 1.67 |
7 | 9 | 1.29 |
| 29.00 | 5.25 |
HM = 29/5.25 = 5.5
Example 5 – calculate harmonic mean
class | frequency |
2-4 | 3 |
4-6 | 4 |
6-8 | 2 |
8-10 | 1 |
Solution
class | frequency | x | f/x |
2-4 | 3 | 3 | 1 |
4-6 | 4 | 5 | 0.8 |
6-8 | 2 | 7 | 0.28 |
8-10 | 1 | 9 | 0.11 |
| 10 |
| 2.19 |
Harmonic mean = 10/2.19 = 4.55
Merits of mean
- It is rigidly defined
- It is easy to understand and easy to calculate
- It is based upon all values of the given data
- It is capable of future mathematical treatment
- It is not much affected by sampling fluctuation
Demerits of mean
- It cannot be calculated if any observation are missing
- It cannot be calculated for open end classes
- It is effected by extreme values
- It cannot be located graphically
- It may be number which is not present in the data
1.5 Permutation and Combination.
Permutations-
A permutation of n objects taken r at a time is an arrangement of r of the objects
(r≤n).
The symbols of permutations of n things taken r at a time are- 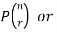
Example 1: Consider the three letters x, y, z. The arrangements of the letter x, y, ztaken two at a time are-
xy, yx, xz, zx, yz, zy
∴The number of 2-arrangements are 6 i.e., the number of permutation of 3 letters taken 2 at a time
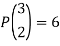
Note-A permutation of n objects taken r at a time is also called r-permutation
Factorial function-
The product of the positive integers from 1 to n is denoted by n!and we read it as “factorial “
Expressed as-
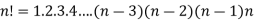
Note- 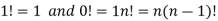
Binomial coefficient-
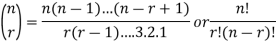
Example:
1. 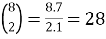

Permutation-
The arrangement of a set of n objects in a given order is called a permutation.
Any arrangement of any 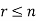 of these objects in a given order is said to be r-permutation.
of these objects in a given order is said to be r-permutation.
The number of permutations of n objects taken r will be denoted as-
P(n, r)
Formula- 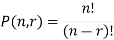
Permutation with repetitions-
The number of permutations of n objects of which are 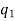 are alike,
are alike, 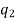 are alike,
are alike, 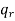
are alike is-
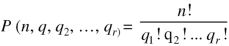
Sampling with or without replacement-
Suppose we chose the samples with repetition, from example if we draw a ball from a urn then we put back that ball in the urn and again we pick a ball and we continue the process, so this is the case of sampling with repetition
Then the product rule tells us that the number of such samples is-
n.n.n.n.n……….n.n = 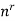
And if we pick a ball from the urn and we do not put it back to the urn, then this is the case of sampling without replacement.
So that in this case the number of samples are given as-

Example-
Three cards are chosen one after the other from a 52-card deck. Find the number m of ways
This can be done: (a) with replacement; (b) without replacement.
Sol.
(a) Each card can be chosen in 52 ways. Thus m = 52(52)(52) = 140 608.
(b) Here there is no replacement. Thus the first card can be chosen in 52 ways, the second in 51 ways, and the third in 50 ways. So that-
P(52, 3) = 52(51)(50) = 132 600
Example-
There are 4 black, 3 green and 5 red balls. In how many ways can they be arranged in a row?
Solution: Total number of balls = 4 black + 3 green + 5 red = 12
The black balls are alike,
The green balls are, and the red balls are alike,
The number of ways in which the balls can be arranged in a row =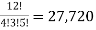
Example- A box contains 10 light bulbs. Find the number n of ordered samples of:
(a) Size 3 with replacement,
(b) Size 3 without replacement.
Solution:
(a) n= 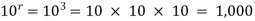
(b) P (10, 3) = 10 × 9 × 8 = 720
Circular permutations-
A circular permutation of n objects is an arrangement of the objects around a circle.
If the n objects are to be arranged round a circle we take an objects and fix it in one position.
Now the remaining (n – 1) objects can be arranged to fill the (n – 1) positions the circle in (n – 1)! ways.
Hence the number of circular permutations of n different objects = (n – 1)!
Combinations-
A combination of n objects taken at a time is an unordered selection of r of the n
Objects (r ≤n).
A combination of n objects taken r at a time is also called r-combination of n objects.
The number of combinations is given by-
C(n, r)
Note-
1. property-1
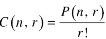
2. property-2
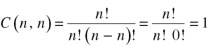
3. property-3
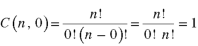
Example: From a class of 3 students, 4 students are to be chosen for competition, in how many ways they can be selected?
Sol.
The number of combinations will be-
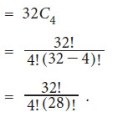
Example:

Sol.
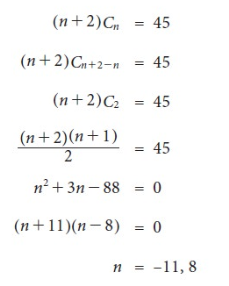
n = -11 is not possible,
therefore-
n = 8
Example:
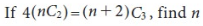
Sol.
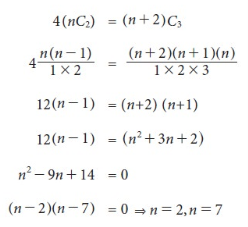
Key takeaways-
- Permutations-
A permutation of n objects taken r at a time is an arrangement of r of the objects
(r≤n).
The symbols of permutations of n things taken r at a time are- 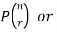
2. Binomial coefficient-
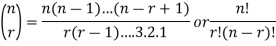
3. Permutation-
The arrangement of a set of n objects in a given order is called a permutation.
Any arrangement of any 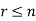 of these objects in a given order is said to be r-permutation.
of these objects in a given order is said to be r-permutation.
4. Circular permutations-
A circular permutation of n objects is an arrangement of the objects around a circle.
If the n objects are to be arranged round a circle we take an objects and fix it in one position.
5. Combinations-
A combination of n objects taken at a time is an unordered selection of r of the n
Objects (r ≤n).
References
- Mathematics and Statistics for Business – R. S. Bhardwaj – Excel Books.
- Business Mathematics and Statistics – Subhanjali Chopra – Pearson publication.
- Fundamentals of Business Mathematics and Statistics – ICAI – ICAI.
- Business Mathematics and Statistics – Dr. J K Das, N Das – McGraw Hill Education.
