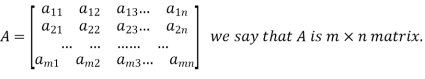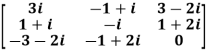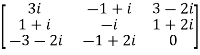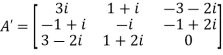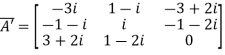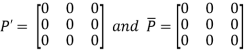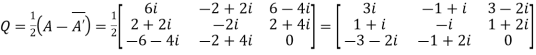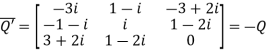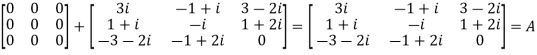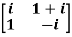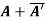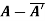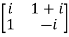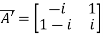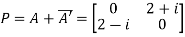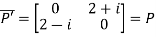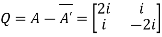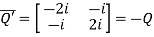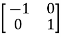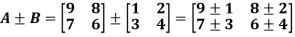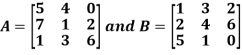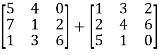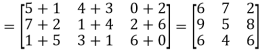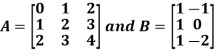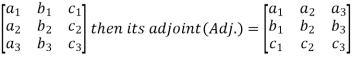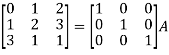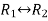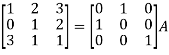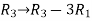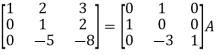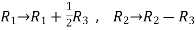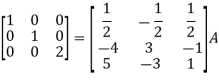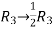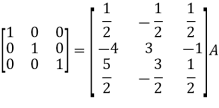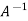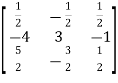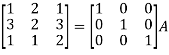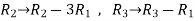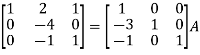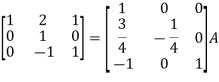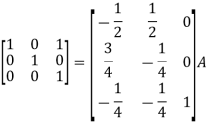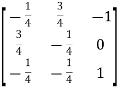UNIT – III
Matrices
3.1 Matrices: Addition, Subtraction, Multiplication of matrices
Matrices have wide range of applications in various disciplines such as chemistry, Biology, Engineering, Statistics, economics, etc. Matrices play an important role in computer science also. Matrices are widely used to solving the system of linear equations, system of linear differential equations and non-linear differential equations. First time the matrices were introduced by Cayley in 1860.
Definition-
A matrix is a rectangular arrangement of the numbers.
These numbers inside the matrix are known as elements of the matrix.
A matrix ‘A’ is expressed as-
|
The vertical elements are called columns and the horizontal elements are rows of the matrix.
The order of matrix A is m by n or (m× n)
Notation of a matrix-
A matrix ‘A’ is denoted as-
A = 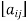
Where, i = 1, 2, …….,m and j = 1,2,3,…….n
Here ‘i’ denotes row and ‘j’ denotes column.
Types of matrices-
1. Rectangular matrix-
A matrix in which the number of rows is not equal to the number of columns, are called rectangular matrix.
Example:
A = 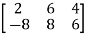
The order of matrix A is 2×3 , that means it has two rows and three columns.
Matrix A is a rectangular matrix.
2. Square matrix-
A matrix which has equal number of rows and columns, is called square matrix.
Example:
A = 
The order of matrix A is 3 ×3 , that means it has three rows and three columns.
Matrix A is a square matrix.
3. Row matrix-
A matrix with a single row and any number of columns is called row matrix.
Example:
A = 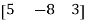
4. Column matrix-
A matrix with a single column and any number of rows is called row matrix.
Example:
A = 
5. Null matrix (Zero matrix)-
A matrix in which each element is zero, then it is called null matrix or zero matrix and denoted by O
Example:
A = 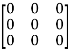
6. Diagonal matrix-
A matrix is said to be diagonal matrix if all the elements except principal diagonal are zero
The diagonal matrix always follows- 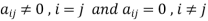
Example:
A = 
7. Scalar matrix-
A diagonal matrix in which all the diagonal elements are equal to a scalar, is called scalar matrix.
Example-
A = 
8. Identity matrix-
A diagonal matrix is said to be an identity matrix if its each element of diagonal is unity or 1.
It is denoted by – ‘I’
I = 
9. Triangular matrix-
If every element above or below the leading diagonal of a square matrix is zero, then the matrix is known as a triangular matrix.
There are two types of triangular matrices-
(a) Lower triangular matrix-
If all the elements below the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.
Example:
A = 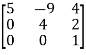
(b) Upper triangular matrix-
If all the elements above the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.
Example-
A = 
Special types of matrices-
Symmetric matrix-
Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
For example:
 and
and 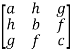
Example: check whether the following matrix A is symmetric or not?
A = 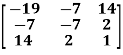
Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.
So that, first we will find its transpose,
Transpose of matrix A ,
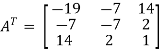
Here,
A = 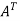
The matrix A is symmetric.
Example: Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.
Sol. Suppose A is any square matrix.
Then,
A = 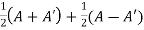
Now,
(A + A’)’ = A’ + A
A+A’ is a symmetric matrix.
Also,
(A - A’)’ = A’ – A
Here A’ – A is an anti – symmetric matrix
So that,
Square matrix = symmetric matrix + anti-symmetric matrix
Hermitian matrix:
A square matrix A = 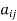 is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
It means,
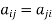
For example:
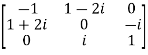
Necessary and sufficient condition for a matrix A to be hermitian –
A = (͞A)’
Skew-Hermitian matrix-
A square matrix A = 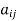 is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.
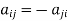
Note- all the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.
For example:
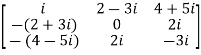
The necessary and sufficient condition for a matrix A to be skew hermitian will be as follows-
- A = (͞A)’
Note: A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian.
Similarly a Skew- Hermitian matrix is a generalization of a Skew symmetric matrix and also every Skew- symmetric matrix is Skew –Hermitian.
Theorem: Every square complex matrix can be uniquely expressed as sum hermitian and skew-hermitian matrix.
Or If A is given square complex matrix then 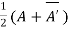 is hermitian and
is hermitian and 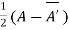 is skew-hermitian matrices.
is skew-hermitian matrices.
Example1: Express the matrix A as sum of hermitian and skew-hermitian matrix where
Let A = Therefore Let Again Hence P is a hermitian matrix. Let Again Hence Q is a skew- hermitian matrix. We Check P +Q= Hence proved.
Example2: If A = (i) (ii)
Sol. Given A = Then Let Also Hence P is a Hermitian matrix. Let Also Hence Q is a skew-hermitian matrix. |
Skew-symmetric matrix-
A square matrix A is said to be skew symmetrix matrix if –
1. A’ = -A, [ A’ is the transpose of A]
2.all the main diagonal elements will always be zero.
For example-
A = 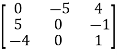
This is skew symmetric matrix, because transpose of matrix A is equals to negative A.
Example: check whether the following matrix A is symmetric or not?
A = 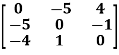
Sol. This is not a skew symmetric matrix, because the transpose of matrix A is not equals to -A.
-A = A’
Orthogonal matrix-
Any square matrix A is said to be an orthogonal matrix if the product of the matrix A and its transpose is an identity matrix.
Such that,
A. A’ = I
Matrix × transpose of matrix = identity matrix
Note- if |A| = 1, then we can say that matrix A is proper.
Examples: |
Unitary matrix-
A square matrix A is said to be unitary matrix if the product of the transpose of the conjugate of matrix A and matrix itself is an identity matrix.
Such that,
( ͞A)’. A = I
For example:
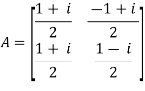
and its
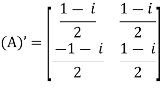
Then (͞A)’ . A = I
So that we can say that matrix A is said to be a unitary matrix.
Key takeaways-
- The matrices were introduced by Cayley in 1860.
- A matrix ‘A’ is denoted as-
A = 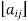
Where, i = 1, 2, …….,m and j = 1,2,3,…….n
Here ‘i’ denotes row and ‘j’ denotes column.
3. Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
4. Square matrix = symmetric matrix + anti-symmetric matri
5. A square matrix A = 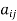 is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
6. All the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.
7. A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian
8. Every square complex matrix can be uniquely expressed as sum hermitian and skew-hermitian matrix.
9. A square matrix A is said to be skew symmetrix matrix if –
(a) A’ = -A, [ A’ is the transpose of A]
(b) all the main diagonal elements will always be zero.
10. Any square matrix A is said to be an orthogonal matrix if the product of the matrix A and its transpose is an identity matrix.
11. if |A| = 1, then we can say that matrix A is proper.
12. A square matrix A is said to be unitary matrix if the product of the transpose of the conjugate of matrix A and matrix itself is an identity matrix.
Matrix operation ( Addition, scalar multiplication, matrix multiplication, transpose of a matrix)
Algebra on Matrices:
- Addition and subtraction of matrices:
Addition and subtraction of matrices is possible if and only if they are of same order.
We add or subtract the corresponding elements of the matrices.
Example:
Example: Add Sol. A + B =
|
2. Scalar multiplication of matrix:
In this we multiply the scalar or constant with each element of the matrix.
Example: 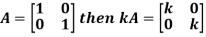
3. Multiplication of matrices: Two matrices can be multiplied only if they are conformal i.e. the number of column of first matrix is equal to the number rows of the second matrix.
Example:
Then |
4. Power of Matrices: If A is A square matrix then
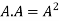
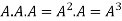 and so on.
and so on.
If 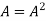 where A is square matrix then it is said to be idempotent.
where A is square matrix then it is said to be idempotent.
5. Transpose of a matrix: The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by 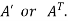
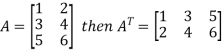
The transpose of matrix 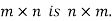 Also
Also 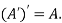
Note: 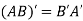
6. Trace of a matrix-
Suppose A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix.
Example- If we have a matrix A-
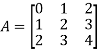
Then the trace of A = 0 + 2 + 4 = 6
Key takeaways-
- Addition and subtraction of matrices is possible if and only if they are of same order.
- Two matrices can be multiplied only if they are conformal i.e. the number of column of first matrix is equal to the number rows of the second matrix.
- If
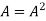 where A is square matrix then it is said to be idempotent.
where A is square matrix then it is said to be idempotent. - The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by
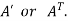
- :
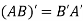
If A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix
3.2 Inverse of matrices
Adjoint of a matix-
Transpose of a co-factor matrix is known as the disjoint matrix.
If the following is a co-factor of matrix A-
|
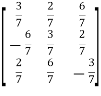
Inverse of a matrix-
The inverse of a matrix ‘A’ can be find as-
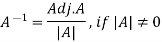
Example: Find the inverse of matrix ‘A’ if-
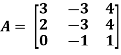
Sol.
Here we have-
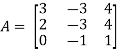
Then
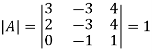
And the matrix formed by its co-factors of |A| is-
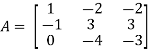
Then
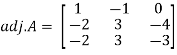
Therefore-
We know that-
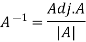
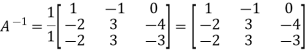
Inverse of a matrix by using elementary transformation-
The following transformation are defined as elementary transformations-
1. Interchange of any two rows (column)
2. Multiplication of any row or column by any non-zero scalar quantity k.
3. Addition to one row (column) of another row(column) multiplied by any non-zero scalar.
The symbol ~ is used for equivalence.
Elementary matrices-
If we get a square matrix from an identity or unit matrix by using any single elementary transformation is called elementary matrix.
Note- Every elementary row transformation of a matrix can be affected by pre multiplication with the corresponding elementary matrix.
The method of finding inverse of a non-singular matrix by using elementary transformation-
Working steps-
1. Write A = IA
2. Perform elementary row transformation of A of the left side and I on right side.
3. Apply elementary row transformation until ‘A’ (left side) reduces to I, then I reduces to 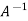
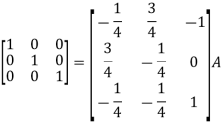
Example-1: Find the inverse of matrix ‘A’ by using elementary transformation- A = Sol. Write the matrix ‘A’ as- A = IA
Apply
Apply
Apply
Apply
Apply
So that,
Example-2: Find the inverse of matrix ‘A’ by using elementary transformation- A = Sol. Write the matrix ‘A’ as- A = IA
Apply
Apply
Apply
Apply
So that
|
Key takeaways-
- Transpose of a co-factor matrix is known as the disjoint matrix.
If the following is a co-factor of matrix A-
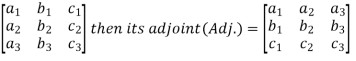
2. 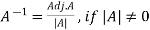
3. If we get a square matrix from an identity or unit matrix by using any single elementary transformation is called elementary matrix.
4. Every elementary row transformation of a matrix can be affected by pre multiplication with the corresponding elementary matrix.
5. The symbol ~ is used for equivalence.
Equations of the form ax+b=0 are called linear equations in the variable x. In this section we will be concerned with the problem of solving linear equations, and equations that reduce to linear equations.
We define two equations as equivalent if they have the same solution set. The following two operations on an equation always result in a new equation which is equivalent to the original one. These operations, sometimes called elementary transformations, are:
T.1 The same expression representing a real number may be added to both sides of an equation.
T.2 The same expression representing a nonzero real number may be multiplied into both sides of an equation.
Using these operations, we may transform an equation whose solution set is not obvious through a series of equivalent equations to an equation that has an obvious solution set.
Example 1. Solve the equation
(a) 2 x-3=4+x
Add − x to both sides to obtain
− x+2 x-3=− x+4+x (T.1)
or x-3=4
Add 3 to both sides to obtain
x-3+3=4+3 (T.1)
or x=7
Since 2 x-3=4+x is equivalent to x-3=4, which, in turn, is equivalent to x=7, whose solution set is obviously {7}, we know that the solution set of (a) is {7}.
Example 2. Solve the equation
(b) 12 x+23=52 x-1
Add − (12) x to both sides to obtain
23=52 x-12 x-1 (T.1)
or 23=2 x-1
Add 1 to both sides to obtain
1+23=2 x (T.1)
or 53=2 x
Multiply both sides by 12 to obtain
56=x (T.2)
Thus, the solution set of (b) is {56}.
Every linear equation can be solved in the same way as in the above examples. In fact, let us consider the general linear equation
ax+b=0
Add − b to both sides to obtain
ax=− b
Multiply both sides by 1a to obtain
x=− (ba)
if a a≠0. The general linear equation, therefore, has as its solution set {ba}, if a≠0. Thus each linear equation has at most one solution.
The next two examples are of equations that reduce to linear equations.
Example 3. Solve the equation
23+4 y (5 y+4)=9+10 y (2 y+3)
We expand both sides to obtain
23+20 y2+16 y=9+20 y2+30 y
Add − 20 y2 to both sides to obtain
23+16 y=9+30 y
We now solve as in the previous examples.
23+16 y=9+30 y
23-9=30 y-16 y
14=14 y
y=1
Thus, the solution set is {1}.
Example 4. Solve the equation
(c) 2 xx-1=2x-1+1
The replacement set of (c) is all real numbers except 1. Assuming that x≠1, we multiply both sides of (c) by x-1 to obtain
(d) 2 x=2+x-1, x≠1
Solving the equation 2 x=2+x-1, we obtain 1 as the only solution Since 1 is not in the replacement of (d), (d) has no solution. Furthermore, (c) is equivalent to (d), therefore (c) has no solution.
Example 5. If 2 times a certain integer is added to the next consecutive integer the result is 34. Find the integers.
Solution:
Let x be the first integer.
Then x+1 is the next consecutive integer.
2 times a certain integer plus the next consecutive integer is 34.
Then, 2 x+(x+1) =34
3 x+1=34
3 x=33
x=11
Check. 2·11+(11+1)=34
Example 6. Bob and Joe together earned $60. Both were paid at the same rate, but Bob worked three times as long as Joe. How much did each receive?
Solution:
Let x be the number of dollars that Joe received.
Then 3 x is the number of dollars that Bob received
Bob and Joe together earned $60.
3 x+x=60
4 x=60
x=15
3 x=45
Check 3·15+15=60
Example 7. The sum of the digits of a two-digit number is 12. If the digits are reversed the number is decreased by 36. What is the number?
Solution:
Let x be the tens digit.
Then 12-x is the unit’s digit.
If the digits are reversed then the number is decreased by 36
Then, 10 (12-x)+x=10 x+(12-x)-36
=120-10 x+x=10 x+12-x-36
=120-9 x=9 x-24
=144=18 x
=x=8
=12-x=4
Therefore, the number is84.
Check. 84-36=48
Example 8. How many pounds of candy valued at 48¢ per pound should be added to 50 pounds of candy valued at 80¢ per pound in order for the store owner to be able to sell the candy at 60¢ per pound?
Solution: Let x be the number of pounds of 48¢ per pound candy.
Then 50+x would be the pounds of candy he would have at 60¢ per pound.
The amount of candy at 48¢ per pound times 48¢, plus the amount of candy at 80¢ per pound times 80¢, must be equal to the amount of candy at 60¢ per pound times 60¢.
(48¢/lb)(x lbs) + (80¢/lb) (50 lbs) = (60¢/lb) [(50+x)lbs]
Then, 48 x+80·50=60 (50+x)
48 x+4000=3000+60 x
1000=12 x
x=(83 13)lbs
Check. (83+13) 48+80·50=60 (50+83+13)
Problems involving velocities (or speeds) will use the formula
d=rt
where d is the distance travelled, r is the rate, and t is the time. When the formula is used, d and r must be expressed in the same unit of distance, while r and t must be expressed in the same unit of time.
Example 9. A group of students drove to a lake in the north woods to fish. They traveled 380 miles in 7 hours, of which 4 hours were on a paved highway and the remaining time was on a dirt road. If the average speed on the dirt road was 25 miles per hour less than the average speed on the highway, then find for each part of the trip the average speed and the distance travelled.
Solution:
Let x be the speed on the dirt road.
Then x+25 is the speed on the highway.
The distance travelled on the highway plus the distance travelled on the dirt road is equal to 380 miles.
Since d=rt, we have
[(x+25) mihr] (4 hrs)+[x mihr] (3 hrs)=380 mi
(x+25) 4+3 x=380
4 x+100+3 x=380
7 x=280
x=40 miles per hour
x+25=65miles per hour
Check. (40+25) 4+40·3=380
Work problems which involve the rate of performance can often be solved by first finding the fractional part of the task done by each person or machine in one unit of time, and then finding an equation that relates these various fractional parts.
Key Takeaways:
- Equations of the form ax+b=0 is called linear equations in the variable x.
References
- Mathematics and Statistics for Business – R. S. Bhardwaj – Excel Books.
- Business Mathematics and Statistics – Subhanjali Chopra – Pearson publication.
- Fundamentals of Business Mathematics and Statistics – ICAI – ICAI.
- Business Mathematics and Statistics – Dr. J K Das, N Das – McGraw Hill Education.