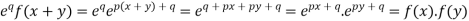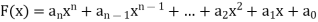UNIT – IV

Functions

4.1 Functions: Types of functions

There are two broad types of functions- algebraic and transcendental functions.

Algebraic function: A function in the form of a polynomial with finite number of terms is known as algebraic function.

Domain and Range of a Function:

The set of values of independent variables x is called the ‘Domain’ of the function and the set of corresponding values of f(x) i.e. the dependent variable y is called the ‘Range’ of the function. These functions can be constructed using only a finite number of elementary operations, such as plus, minus, multiplication and division.

Polynomial Function-

A polynomial in the variable x is a function that can be written in the form-

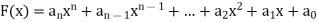
Here 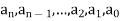are constant.

The term containing the highest power of x are called the leading term

The degree of the polynomial is the power of x in the leading term degree 0, 1, and 2 are polynomials which are constant, linear and quadratic functions while degree 3, 4, and 5 are polynomials with special names: cubic, quartic, and quintic functions. Polynomials with degree n > 5 are just called 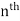degree polynomials.

Constant Function: A constant function is a linear function for which the range does not change no matter which member of the domain is used.

Linear Function: Linear functions are those whose graph is a straight line.

A linear function has the following form. y = f(x) = a + bx.

Quadratic Function: A quadratic function is one of the forms: f(x) = 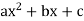, where a, b, and c are numbers with a ≠ 0

Power Function: A power function is a function that can be represented in

the form:

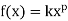
where k and pare real numbers, and x is known as the coefficient

Rational Function-

A rational function is defined by a rational fraction, i.e., an algebraicfraction such that both the numerator and the denominator are polynomials.

Note- the value of denominator should not be equal to zero.

Example: Find the domain and range of the function f(x) =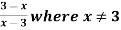

Sol.

f(0) = 3/-3  = -1

f(1) = -1

f(2) = -1

f(3) = -1

so that the domain is = {-1, 0, 1, 2, 4,….} and range = {-1, -1, -1, -1,…..}

Example: find the value of f(2), f(0) and f(3) of the given function-

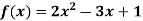
Sol.

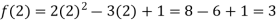
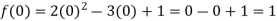
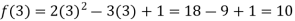
Example: if f(x) = then prove that

Sol.

By taking LHS-

Hence proved

Key takeaways-

Domain and Range of a Function:

1.               The set of values of independent variables x is called the ‘Domain’ of the function and the set of corresponding values of f(x) i.e. the dependent variable y is called the ‘Range’ of the function
2.               Polynomial Function-

A polynomial in the variable x is a function that can be written in the form-

Here 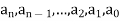are constant.

The term containing the highest power of x are called the leading term

3.                  Constant Function: A constant function is a linear function for which the range does not change no matter which member of the domain is used.

4.                  Power Function: A power function is a function that can be represented in

the form:

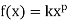
where k and p are real numbers, and x is known as the coefficient

4.2 Applications of linear functions in business

Linear functions are prevalent throughout business and economics. They provide a simple way to model economic quantities. Even if a linear function is not the best type of function to model a quantity, often they are used as an initial model to help understand a situation and all of its complexities.

The linear function is popular in economics. It is attractive because it is simple and easy to handle mathematically. It has many important applications.

Linear functions are those whose graph is a straight line.

A linear function has the following form

y = f(x) = a + bx

A linear function has one independent variable and one dependent variable. The independent variable is x and the dependent variable is y.

a is the constant term or the y intercept. It is the value of the dependent variable when x = 0.

b is the coefficient of the independent variable. It is also known as the slope and gives the rate of change of the dependent variable.

Graphing a linear function

To graph a linear function:

1. Find 2 points which satisfy the equation

2. Plot them

3. Connect the points with a straight line

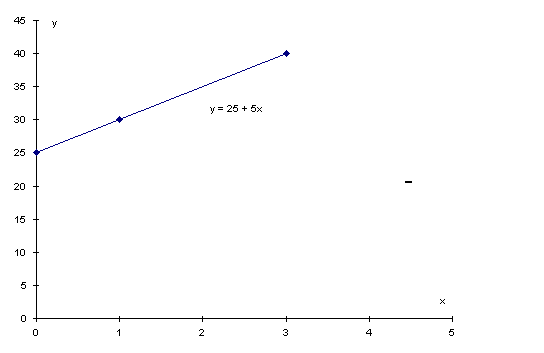
Example:

y = 25 + 5x

let x = 1
then
y = 25 + 5(1) = 30

let x = 3
then
y = 25 + 5(3) = 40

A simple example of a linear equation

A company has fixed costs of $7,000 for plant and equipment and variable costs of $600 for each unit of output.
What is total cost at varying levels of output?

let x = units of output
let C = total cost

C = fixed cost plus variable cost = 7,000 + 600 x

Combinations of linear equations

Linear equations can be added together, multiplied or divided.

A simple example of addition of linear equations

C(x) is a cost function

C(x) = fixed cost + variable cost

R(x) is a revenue function

R(x) = selling price (number of items sold)

profit equals revenue less cost

P(x) is a profit function

P(x) = R(x) - C(x)

x = the number of items produced and sold

Data:

A company receives $45 for each unit of output sold. It has a variable cost of $25 per item and a fixed cost of $1600.
What is its profit if it sells (a) 75 items, (b)150 items, and (c) 200 items?

 Key Takeaways:

1. A linear function has one independent variable and one dependent variable. The independent variable is x and the dependent variable is y.
2. Linear functions are those whose graph is a straight line.

4.3 Simple equations

Problem 1:

18 is taken away from 8 times of a number is 30. Find the number. 

Solution:

Let "x" be the number. 

Given: 18 is taken away from 8 times of the number is 30

Then, we have

8x - 18 = 30

Add 18 to both sides.

8x = 48

Divide both sides by 8.

x = 6 

Hence, the number is 6.

Problem 2:

The denominator of a fraction exceeds the numerator by 5. If 3 be added to both, the fraction becomes 3/4. Find the fraction. 

Solution:

Let "x" be the numerator. 

"The denominator of the fraction exceeds the numerator"

From the above information,

Fraction = x / (x + 5) ----------(1)

"If 3 be added to both, the fraction becomes 3 / 4"

From the above information, we have

(x+3) / (x + 5 + 3) = 3 / 4

Simplify.

(x + 3) / (x + 8) = 3/4

4(x + 3) = 3(x + 8)

4x + 12  =  3x + 24

x = 12

Plug x = 12 in (1)

Fraction = 12 / (12 + 5)

Fraction = 12 / 17

Hence, the required fraction is 12 / 17. 

Problem 3:

If thrice of A's age 6 years ago be subtracted from twice his present age, the result would be equal to his present age. Find A's present age. 

Solution:

Let "x" be A's present age.

A's age 6 years ago = x - 6

Thrice of A's age 6 years ago = 3(x-6) 

Twice his present age = 2x

Given: Thrice of A's age 6 years ago be subtracted from twice his present age, the result would be equal to his present age.

So, we have

2x - 3(x - 6) = x

Simplify.

2x - 3x + 18 = x

- x + 18 = x

18 = 2x

Divide both sides by 2.

9 = x

Hence, A's present age is 9 years.

Problem 4:

A number consists of two digits. The digit in the tens place is twice the digit in the unit’s place. If 18 be subtracted from the number, the digits are reversed. Find the number.   

Solution:

Let "x" be the digit in unit’s place.

Then, the digit in the tens place=2x

So, the number is (2x) x.

Given: If 18 be subtracted from the number, the digits are reversed. 

So, we have

(2x) x - 18 = x(2x)

(2x) x - 18 = x(2x)

10 ⋅ (2x) + 1 ⋅ x - 18 = 10 ⋅ x + 1 ⋅ (2x)

Simplify.

20x + x - 18 = 10x + 2x

21x - 18 = 12x

21x - 18 = 12x

9x = 18

Divide both sides by 9. 

x = 2

The digit at the unit’s place is 2.

Then, the digit at the tens place is

= 2 ⋅ 2

= 4

Hence the required number is 42.

Problem 5:

For a certain commodity, the demand equation giving demand "d" in kg, for a price "p" in dollars per kg. is d = 100(10 - p). The supply equation giving the supply "s" in kg. for a price "p" in dollars per kg is s = 75(p - 3). Find the equilibrium price.

Solution:

The equilibrium price is the market price where the quantity of goods demanded is equal to the quantity of goods supplied. 

So, we have 

d = s

100(10 - p) = 75(p - 3) 

Simplify.

1000 - 100p = 75p - 225

 1225 = 175p

Divide both sides by 175.

7 = p 

Hence, the equilibrium price is $7.

Problem 6:

The fourth part of a number exceeds the sixth part by 4. Find the number.

Solution:

Let "x" be the required number. 

Fourth part of the number = x/4

Sixth part of the number = x/6 

Given: The fourth part of a number exceeds the sixth part by 4. 

x/4 - x/6 = 4

L.C.M of (4, 6) is 12. 

(3x/12) - (2x/12) = 4

Simplify.

(3x - 2x) / 12 = 4

x / 12 = 4

Multiply both sides by 12. 

x = 48

Hence, the required number is 48. 

Problem 7:

The width of the rectangle is 2/3 of its length. If the perimeter of the rectangle is 80 cm. Find its area. 

Solution:

Let "x" be the length of the rectangle. 

Then, width of the rectangle is 2x / 3

Given: Perimeter is 80cm. 

Perimeter = 80 cm

2 ⋅ (l + w) = 80

Divide both sides by 2. 

l + w = 40

Plug l = x and w = 2x / 3.

x + 2x / 3 = 40

Simplify.

(3x + 2x) / 3 = 40

5x / 3 = 40

Multiply both sides by 3/5.

x = 24

The length is 24 cm. 

Then, the width is

= 2x / 3

= (2 ⋅ 24) / 3

= 16 cm

Formula to find the area of a rectangle is

= l ⋅ w

Plug l = 24 and w = 16. 

= 24 ⋅ 16

= 384

Hence, area of the rectangle is 384 square cm.

Problem 8:

In a triangle, the second angle is 5° more than the first angle. And the third angle is three times of the first angle. Find the three angles of the triangle. 

Solution:

Let x° be the first angle.

Then, we have 

the second angle = x° + 5°

third angle = 3 ⋅ x°

We know that the sum of three angle in any triangle is 180°.

x° + (x° + 5°) + (3 ⋅ x°) = 180°

x + x + 5 + 3x  =  180

Simplify. 

5x + 5 = 180

Subtract 5 from both sides. 

5x = 175

Divide both sides by 5.

x = 35

The first angle is 35°. 

The second angle is

= 35° + 5°

= 40°

The third angle is 

= 3 ⋅ 35°

= 105°

Hence, the three angles of the triangle are 35°, 40° and 105°.

4.4 Quadratic equations

Definition of Quadratic Equation

Usually, the quadratic equation is represented in the form of ax2+bx+c=0, where x is the variable and a,b,c are the real numbers & a ≠ 0. Here, a and b are the coefficients of x2 and x, respectively. So, basically a quadratic equation is a polynomial whose highest degree is 2. Let us see some examples:

• 3x2+x+1, where a=3, b=1, c=1
• 9x2-11x+5, where a=9, b=-11, c=5

Roots of Quadratic Equations:

If we solve any quadratic equation, then the value we obtained are called the roots of the equation. Since the degree of the quadratic equation is two, therefore we get here two solutions and hence two roots.

There are different methods to find the roots of quadratic equation, such as:

• Factorisation
• Completing the square
• Using quadratic formula

Quadratic Equation Formula:

The quadratic formula to find the roots of the quadratic equation is given by:

x=−b±b2−4ac√2a

Where, b2-4ac is called discriminant of the equation.

Based on the discriminant value, there are three possible conditions, which defines the nature of roots as follows:

• two distinct real roots, if b2 – 4ac > 0
• two equal real roots, if b2 – 4ac = 0
• no real roots, if b2 – 4ac < 0

Quadratic Equations Problems and Solutions

1. Rahul and Rohan have 45 marbles together. After losing 5 marbles each, the product of the number of marbles they both have now is 124. How to find out how many marbles they had to start with.

Solution: Say, the number of marbles Rahul had be x.

Then the number of marbles Rohan had = 45 – x.

The number of marbles left with Rahul after losing 5 marbles = x – 5

The number of marbles left with Rohan after losing 5 marbles = 45 – x – 5 = 40 – x

The product of number of marbles = 124

(x – 5) (40 – x) = 124

40x – x2 – 200 + 5x = 124

– x2 + 45x – 200 = 124

x2 – 45x + 324 = 0

This represents the problem mathematically.

2. Check if x (x + 1) + 8 = (x + 2) (x – 2) is in the form of quadratic equation.

Solution: Given,

x (x + 1) + 8 = (x + 2) (x – 2)

x2+x+8 = x2-22 [By algebraic identities]

Cancel x2 both the sides.

x+8=-4

x+12=0

Since, this expression is not in the form of ax2+bx+c, hence it is not a quadratic equation.

3. Find the roots of the equation 2x2 – 5x + 3 = 0 using factorisation.

Solution: Given,

2x2 – 5x + 3 = 0

2x2 – 2x-3x+3 = 0

2x(x-1)-3(x-1) = 0

(2x-3) (x-1) = 0

So,

2x-3 = 0; x = 3/2

(x-1) = 0; x=1

Therefore, 3/2 and 1 are the roots of the given equation.

4. Solve the quadratic equation 2x2+ x – 300 = 0 using factorisation.

Solution: 2x2+ x – 300 = 0

2x2 – 24x + 25x – 300 = 0

2x (x – 12) + 25 (x – 12) = 0

(x – 12) (2x + 25) = 0

So,

x-12=0; x=12

(2x+25) = 0; x=-25/2 = -12.5

Therefore, 12 and -12.5 are two roots of given equation.

5. Solve the equation x2+4x-5=0, using completing the square method.

Solution:

x2 + 4x – 5 = 0

x2+8/2x-5 = 0

x2+4/2x+4/2x-5 = 0

x2+2x+2x-5 = 0

(x + 2) x + 2 × x – 5= 0

(x + 2) x + 2 × x + 2 × 2 – 2 × 2 – 5= 0

(x + 2) x + (x + 2) × 2 – 2 × 2 – 5 = 0

(x+2) (x+2) -22 – 5 = 0

(x+2)2 – 22 – 5 = 0

(x+2)2 – 4 – 5 = 0

(x+2)2 – 9 = 0

(x+2)2 – 32 = 0

(x+2+3) (x+2-3) = 0 [By algebraic identities]

(x+5) (x-1) = 0

Therefore,

x=-5 & x=1

6. Solve the quadratic equation 2x2 + x – 528 = 0, using quadratic formula.

Solution: If we compare it with standard equation, ax2+bx+c = 0

a=2, b=1 and c=-528

Hence, by using the quadratic formula:

x=−b±b2−4ac√2a

Now putting the values of a,b and c.

x=−1±1+4(2)(528)√4=−1±4225√4=−1±654

x=64/4 or x=-66/4

x=16 or x=-33/2

7. Find the roots of x2 + 4x + 5 = 0, if any exist, using quadratic formula.

Solution: To check whether there are real roots available for the quadratic equation, we need the find the discriminant value.

D = b2-4ac = 42-4.1.5 = 16-20 = -4

Since square root of -4 will not give real number. Hence there is no real roots for the given equation.

8. Find the discriminant of the equation: 3x2-2x+⅓ = 0.

Solution: Here, a = 3, b=-2 and c=⅓

Hence, discriminant, D = b2 – 4ac

D = (-2)2-4.3.(⅓)

D = 4-4

D=0

Key Takeaways:

1. Usually, the quadratic equation is represented in the form of ax2+bx+c=0, where x is the variable and a,b,c are the real numbers & a ≠ 0.
2. The quadratic formula to find the roots of the quadratic equation is given by:

x=−b±b2−4ac√2a

Where, b2-4ac is called discriminant of the equation.

4.5 Simultaneous equations and problems thereon

Equation – Equations signify relation of equality between two algebraic expressions symbolized by the sign of equality ‘=’. In other words, an equation is statement which says that the two algebraic expressions are equal and is satisfied only for certain values of the variables.

Identify – When equality of two algebraic expressions hold true for all values of variables then it is called an identity.

Root of an Equation – The value of unknown or variable for which the equation is true is known as the root of the equation. To find the roots of an equation means to solve the equations.

Degree of an Equation – The degree of an equation is the highest exponent of the variable x or variables (x, y, …) present in the equation is called the degree of an equation.

Linear Equation – An equation which involves power of an unknown quantity not higher than unity (one) is called a linear equation.

One variable Linear Equation – A linear equation in one variable (x, say) in which the highest degree of the variable x is 1.

A linear equation in one variable is, in general, written as ax+by = c or ax = c. This equation is also called, “First degree equation in x” or simple equation.

Two variable equation – A linear equation in two variables (x, y, say) in which the highest degree of the variables x and y each is 1. A linear equation in two variables, is general, is written as

ax+by+c = 0

Or

ax+by=d.

Three variable equation – A linear equation in three variables (x, y, z, say) in which the highest degree of the variables x, y and z each is 1. A linear equation in three variables, in general, is written as a1x+b1y+c1z=d.

Characteristics of Simultaneous Equations

1) A system of linear equations in one variable is not taken under simultaneous equations.

2) The set of values of two variables x and y which satisfy each equation in the system of equations is called the solution of simultaneous equations.

The solutions of two variable linear simultaneous equations may be –

i) Infinitely many,

ii) A unique solution, or

iii) No solution.

3) For simultaneous equations –

a1x + b1y = c1 and a2x + b2y = c2

a. If 𝑎1𝑎2=𝑏1𝑏2=𝑘 𝑎𝑛𝑑 𝑐1=𝑘 C2 then there are infinitely many solutions.

b. If 𝑎1𝑎2=𝑏1𝑏2=𝑐1 ≠ kc2, then there is no solution.

c. If c2 ≠ 0, then c1 = kc2  𝑐1𝑐2=𝑘, ℎ𝑒𝑛𝑐𝑒

𝑎1𝑎2=𝑏1𝑏2=𝑐1𝑐2→𝑖𝑛𝑓𝑖𝑛𝑖𝑡𝑒𝑙𝑦 𝑚𝑎𝑛𝑦 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛𝑠 𝑎𝑛𝑑 𝑎1𝑎2=𝑏1𝑏2≠𝑐1𝑐2→𝑛𝑜 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛

d. If c1 and c2 both are zero (i.e., c1=0=c2)

Types of Simultaneous Equations

i) Linear Simultaneous Equations in two Variables – Two linear equations in two variables together are linear simultaneous equations in two variables, e.g.:

4x+y = 2

3x-5y = 18

ii) Linear Simultaneous Equations in three Variables – Three linear equations in three variables together are linear simultaneous equations in three variables, e.g.:

3x+5y-7z = 13

4x+y-12z = 6

2x+9y-3z = 20

iii) Specific type of Simultaneous Equations – The equations in other than linear form is called specific type equations, e.g.:

i)                   quadratic equation: ax2 + bx + c = 0

ii)                 reciprocal equation: 𝑎𝑥+𝑏𝑦 =𝑐

iii)              a 𝑦𝑥 + 𝑐=𝑏𝑦, 𝑒𝑡𝑐.

Examples of using substitution to solve simultaneous equations:

1. 3x + y = 13
   5x -2y = 7
   
   The coefficient of y in Equation 1 is 1. So first we make y the subject of Equation 1:
   
   y = 13 - 3x
   
   Next, substitute this expression for y in Equation 2 and solve for x:

Finally, substitute the solution for x into the expression for y:

y = 13 - 3(3) = 4
y = 4

So the solution to the pair of simultaneous linear equations is (3,4).
 

2.     2x + 4y = 10
2x + y = 4

The coefficient of y in Equation 2 is 1. So first we make y the subject of Equation 2:

y = 4 - 2x

Next, substitute this expression for y in Equation 1 and solve for x:

Finally, substitute the solution for x into the expression for y:

y = 4 - 2(1) = 2
y = 2

So the solution to the pair of simultaneous linear equations is (1,2).
 

3.       x - 5y = 7
2x -4y = 8

The coefficient of x in Equation 1 is 1. So first we make x the subject of Equation 1:

x = 7 + 5y

Next, substitute this expression for x in Equation 2 and solve for y:

Finally, substitute the solution for y into the expression for x:

x = 7 + 5(-1) = 2
x = 2

So the solution to the pair of simultaneous linear equations is (2,-1).
 

4.     2x + 4y = 12
  x + 8y = 30

The coefficient of x in Equation 2 is 1. So first we make x the subject of Equation 2:

x = 30 - 8y

Next, substitute this expression for x in Equation 1 and solve for y:

Finally, substitute the solution for y into the expression for x:

x = 30 - 8(4) = -2
x = -2

So the solution to the pair of simultaneous linear equations is (-2,2).
 

5.     2x - 4y = 10
-4x+5y = -26

None of the coefficients are 1. So we can choose to make any variable the subject.
Let’s make x the subject of Equation 1:

x = (10 + 4y)/2
x = 5 + 2y

Next, substitute this expression for x in Equation 2 and solve for y:

-4(5 + 2y ) + 5y = -26
-20 - 8y + 5y = -26
-3y = -6
y = 2

Finally, substitute the solution for y into the expression for x:

x = 5 + 2(2) = 9
x = 9

So the solution to the pair of simultaneous linear equations is (9,2).
 

6.     6x + 2y = 10
10x - 3y = 12

None of the coefficients are 1. So we can choose to make any variable the subject.
Let’s make y the subject of Equation 2:

y = (12-10x)/(-3)
y = -4 + (10/3) x

Next, substitute this expression for y in Equation 1 and solve for x:

6x + 2(-4 + (10/3) x) = 10
6x - 8 + (20/3) x = 10
(38/3) x = 18
x = 18*(3/38) = 27/19

Finally, substitute the solution for x into the expression for y:

y = -4 + (10/3)/(27/19) = -4 + 270/57 = -228/57 = 270/57 = 42/57 = 14/19

So the solution to the pair of simultaneous linear equations is (27/19,5/19)

Examples of Solved problems of Simultaneous Equations using Elimination Method

1. Solve the following simultaneous equations by using the elimination method:

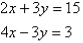
Solution:

Label the equations as follows:

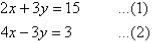
Notice that 3y appears on the left-hand side of both equations.  Adding the left-hand side of (1) and (2), and then the right-hand sides, gives:

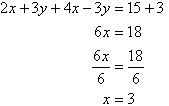
Note:

We have added equals to equals, and addition eliminates y.

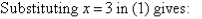
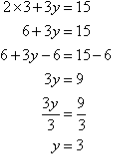
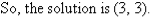
2.     Solve the following simultaneous equations by using the elimination method:

Solution:

Label the equations as follows:

So, the solution is (5, 4)
 

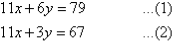
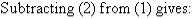
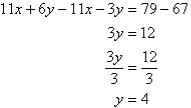
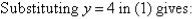
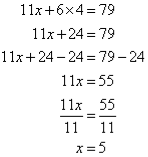
3.     Solve the following simultaneous equations by using the elimination method:

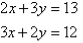
Solution:

Label the equations as follows:

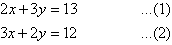
Multiplying (1) by 2 and (2) by 3 gives:

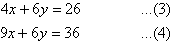
Subtracting (3) from (4) gives:

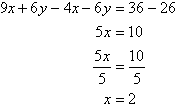
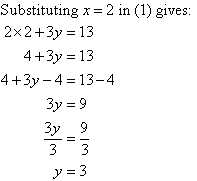
So, the solution is (2, 3).

Equations Containing Fractions

If either or both equations contain fractions, then it is desirable to remove the denominators before solving them simultaneously.

4.     Solve the following simultaneous equations by using the elimination method:

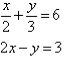
Solution:

Label the equations as follows:

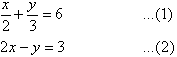
To simplify equation (1), multiply both sides by 6, the lowest common denominator of 2 and 3.

The equations are now:

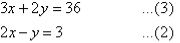
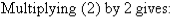
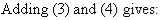
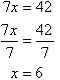
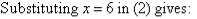
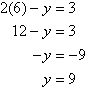
So, the solution is (6, 9).

Key Takeaways:

1. An equation which involves power of an unknown quantity not higher than unity (one) is called a linear equation.
2. One variable Linear Equation – A linear equation in one variable (x, say) in which the highest degree of the variable x is 1.
3. A linear equation in one variable is, in general, written as ax+by = c or ax = c. This equation is also called, “First degree equation in x” or simple equation.

References

1. Mathematics and Statistics for Business – R. S. Bhardwaj – Excel Books.
2. Business Mathematics and Statistics – Subhanjali Chopra – Pearson publication.
3. Fundamentals of Business Mathematics and Statistics – ICAI – ICAI.
4. Business Mathematics and Statistics – Dr. J K Das, N Das – McGraw Hill Education.