Unit 3
Dispersion and Skewness
Central tendency do not reveal the variability present in the data. Dispersion measures the scatteredness of the data series around its average. It tells the variation of the data from one another and gives a clear idea about the distribution of the data.
Definition
In statistics, dispersion is extent to which a distribution is stretched or squeezed.
Characteristics of measures of dispersion
- It should be rigidly defined
- It should be easy to understand and calculate
- Must be based on all observation of the data
- Must be less affected by sampling fluctuation
Types of measures of dispersion
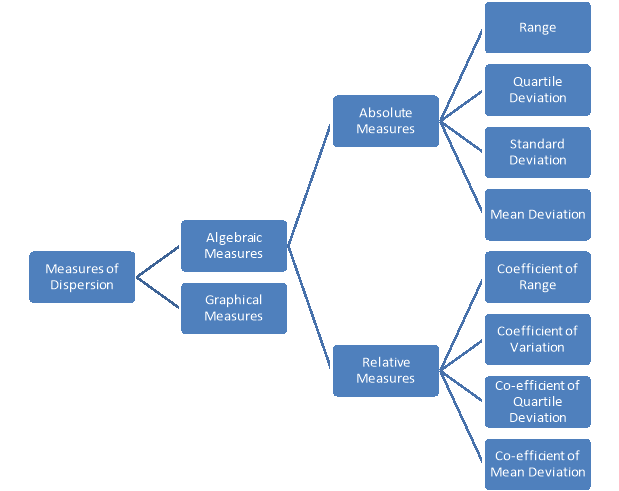
Algebraic measures – It includes the mathematical way to calculate the measures of dispersion.
Graphical measures – The way to calculate the measures of dispersion by graphs and figures.
Absolute measures of dispersion – It gives an idea about the amount of dispersion in a set of observations. It measures the dispersion in the same units as the units of original data. Absolute measures cannot be used for comparison of two or more data set variations.
Relative measures of dispersion – the relative measures of distribution are used for comparing the distribution of two or more data sets.
Coefficients of dispersion are used to compare two series with different measurement of unit.
Types of absolute measures of dispersion
- Range – Range defines the difference between the maximum value and the minimum value given in a data set. More the range , group is more variable. The smaller the range the more homogenous is the group.
R = H – L
Example 1 – 5, 10, 15, 20, 7, 9, 17, 13, 12, 16, 8, 6
Range = H-L
=20 – 5 = 15
Coefficient of range:

Coefficient of range = (15/(20+5))*100 = 60
Example 2 – what is the range for the following set of numbers?
15,21,57,43,11,39,56,83,77,11,64,91,18,37
Solution:
Range = H-L
= 91 – 11 = 80
Therefore, the range is 80
Example 3 – the frequency table shows the number of goals the lakers scored in their last twenty matches. What was the range?
No. Of goals | Frequency |
0 | 2 |
1 | 3 |
2 | 3 |
3 | 6 |
4 | 3 |
5 | 1 |
6 | 1 |
7 | 1 |
Solution:
The range is the difference between the lowest and highest values.
The highest value was 7 (They scored 7 goals on 1 occasion)
The lowest value was 0 (They scored 0 goals on 2 occasions)
Therefore, the range = 7 - 0 = 7
Example 4 – the following table shows the sales of DVD players made by a retail store each month last year
Month | No. Of sales |
January | 25 |
Feb | 43 |
March | 39 |
April | 28 |
May | 29 |
June | 35 |
July | 32 |
August | 46 |
September | 28 |
October | 43 |
November | 51 |
December | 63 |
Solution:
The range is the difference between the lowest and highest values.
The lowest number of sales = 25 in January
The highest number of sales = 63 in December
So, the range = 63 - 25 = 38
Example 5 – what is the range for the following set of numbers?
57, -5, 11, 39, 56, 82, -2, 11, 64, 18, 37, 15, 68
Solution:
The range is the difference between the lowest and highest values.
The highest value is 82.
The lowest value is -5.
Therefore, the range = 82 - (-5) = 82+5 = 87
Merits
- Simple and easy to understand
- It gives a quick answer
Demerits
- It is not based on all observation
- Affected by sampling fluctuations
- It cannot be calculated in open ended distributions
2. Interquartile range - The interquartile range measures the range of the middle 50% of the values only. It is calculated as the difference between the upper and lower quartile.
Interquartile range = upper quartile – lower quartile
= Q3 – Q1
Examples 1– find the interquartile range for 1, 2, 18, 6, 7, 9, 27, 15, 5, 19, 12.
Solution:
Arrange the numbers in ascending order
1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27
Find the median
Median = 9
(1, 2, 5, 6, 7), 9, (12, 15, 18, 19, 27)
Q1 as median in the lower half and Q3 as median in the upper half
Q1 = median in (1, 2, 5, 6, 7)
Q1 = 5
Q3 = median in (12, 15, 18, 19, 27)
Q3 = 18
Interquartile range = 18 – 5 = 13
Example 2 – find the interquartile for the following data set: 3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
Solution:
Arrange the numbers in ascending order
3, 5, 7, 8, 9, 11, 15, 16, 20, 21
Make a mark in the center of the data:
(3, 5, 7, 8, 9,) | (11, 15, 16, 20, 21)
Find the median
Q1 = 7
Q3 = 16
Interquartile range = 16 – 7 = 9
Example 3 - Find the interquartile for the following data set: 1, 3, 4, 5, 5, 6, 7, 11
Make a mark in the center of the data:
(1, 3, 4, 5,) (5, 6, 7, 11)
Find the median
Q1 = (3+4)/2 = 3.5
Q3 = (6+7)/2 = 6.5
Interquartile range = 6.5 – 3.5 = 3
Example 4 -
Find the interquartile range for odd sample size
63,64,64,70,72,76,77,81,81
Solution:
Make a mark in the center of the data:
(63,64,64,70,)72,(76,77,81,81)
Find the median
Q1 = (64+64)/2 = 64
Q3 = (77+81)/2 = 79
Interquartile range = 79 – 64 = 15
Quartile deviation is the product of half of the difference between the upper and the lower quartiles.
QD = (Q3 - Q1) / 2
Coefficient of Quartile Deviation = (Q3 – Q1) / (Q3 + Q1)
Quartile deviation for ungrouped data
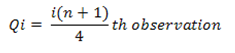
Examples 1
Day | Frequency |
1 | 20 |
2 | 35 |
3 | 25 |
4 | 12 |
5 | 10 |
6 | 23 |
7 | 18 |
8 | 14 |
9 | 30 |
10 | 40 |
Solution:
Arrange the frequency data in ascending order
Day | Frequency |
1 | 10 |
2 | 12 |
3 | 14 |
4 | 18 |
5 | 20 |
6 | 23 |
7 | 25 |
8 | 30 |
9 | 35 |
10 | 40 |
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (10 + 1) /4] th observation
Q1 = 2.75 th observation
Thus, 2.75 th observation lies between the 2nd and 3rd value in the ordered group, between frequency 12 and 14
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 12 + 0.75 * (14 – 12) = 13.50
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (10 + 1) /4] th observation
Q3 = 8.25 th observation
So, 8.25 th observation lies between the 8th and 9th value in the ordered group, between frequency 30 and 35
Third quartile (Q3) is calculated as
Q3 = 8th observation +0.25 * (9th observation – 8th observation)
Q3 = 30 + 0.25 * (35 – 30) = 31.25
Now using the quartiles values Q1 and Q3, we will calculate the quartile deviation.
QD = (Q3 - Q1) / 2
QD = (31.25 – 13.50) / 2 = 8.875
Coefficient of Quartile Deviation = (Q3 – Q1) / (Q3 + Q1)
= (31.25 – 13.50) /(31.25 + 13.50) = 0.397
Example 2– Calculate quartile deviation from the following test scores:
Sl. N o | Test scores |
1 | 17 |
2 | 17 |
3 | 26 |
4 | 27 |
5 | 30 |
6 | 30 |
7 | 31 |
8 | 37 |
Solution:
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (8 + 1) /4] th observation
Q1 = 2.25 th observation
Thus, 2.25 th observation lies between the 2nd and 3rd value in the ordered group, between frequency 17 and 26
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 17 + 0.75 * (26 – 17) = 23.75
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (8 + 1) /4] th observation
Q3 = 6.75 th observation
So, 6.75 th observation lies between the 6th and 7th value in the ordered group, between frequency 30 and 31
Third quartile (Q3) is calculated as
Q3 = 6th observation +0.25 * (7th observation – 6th observation)
Q3 = 30 + 0.25 * (31 – 30) = 30.25
Now using the quartiles values Q1 and Q3, we will calculate the quartile deviation.
QD = (Q3 - Q1) / 2
QD = (30.25 – 23.75) / 2 = 3.25
Quartile deviation for grouped data
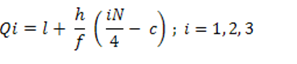
Where,
l = lower boundary of quartile group
h = width of quartile group
f = frequency of quartile group
N = total number of observations
C= cumulative frequency preceding quartile group
Example 3
Age in years | 40 -44 | 45 – 49 | 50 – 54 | 55 - 59 | 60 – 64 | 65 - 69 |
Employees | 5 | 8 | 11 | 10 | 9 | 7 |
Solutions:
In the case of Frequency Distribution, Quartiles can be calculated by using the formula:
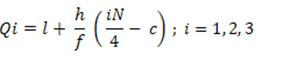
Class interval | F | Class boundaries | CF |
40 -44 | 5 | 39.5 – 44.5 | 5 |
45 – 49 | 8 | 44.5 – 49.5 | 13 |
50 – 54 | 11 | 49.5 – 54.5 | 24 |
55 – 59 | 10 | 54.5 – 59.5 | 34 |
60 – 64 | 9 | 59.5 – 64.5 | 43 |
65 – 69 | 7 | 64.5 – 69.5 | 50 |
Total | 50 |
|
|
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(50)/4]th observation
Q1 = 12.50th observation
So, 12.50th value is in the interval 44.5 – 49.5
Group of Q1 = 44.5 – 49.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (44.5 + ( 5/ 8)* (1* (50/4) – 5)
Q1 = 49.19
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (50) /4] th observation
Q3 = 37.5th observation
So, 37.5th value is in the interval 59.5 – 64.5
Group of Q3 = 59.5 – 64.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (59.5 + ( 5/ 9)* (3* (50/4) – 34)
Q3 = 61.44
QD = (Q3 - Q1) / 2
QD = (61.44 – 49.19) / 2 = 6.13
Coefficient of Quartile Deviation = (Q3 – Q1) / (Q3 + Q1)
= (61.44 – 49.19) /(61.44 + 49.19) = 0.11
Example 4 – Computation of quartile deviation for grouped test scores
Class | Frequency |
9.3-9.7 | 22 |
9.8-10.2 | 55 |
10.3-10.7 | 12 |
10.8-11.2 | 17 |
11.3-11.7 | 14 |
11.8-12.2 | 66 |
12.3-12.7 | 33 |
12.8-13.2 | 11 |
Solution:
Class | Frequency | Class boundaries | CF |
9.3-9.7 | 2 | 9.25-9.75 | 2 |
9.8-10.2 | 5 | 9.75-10.25 | 2 + 5 = 7 |
10.3-10.7 | 12 | 10.25-10.75 | 7 + 12 = 19 |
10.8-11.2 | 17 | 10.75-11.25 | 19 + 17 = 36 |
11.3-11.7 | 14 | 11.25-11.75 | 36 + 14 = 50 |
11.8-12.2 | 6 | 11.75-12.25 | 50 + 6 = 56 |
12.3-12.7 | 3 | 12.25-12.75 | 56 + 3 = 59 |
12.8-13.2 | 1 | 12.75-13.25 | 59 + 1 = 60 |
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(60)/4]th observation
Q1 = 15th observation
So, 15th value is in the interval 10.25-10.75
Group of Q1 = 10.25-10.75
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (10.25 + ( 0.5/ 12)* (1* (60/4) – 7)
Q1 = 10.58
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (60) /4] th observation
Q3 = 45th observation
So, 45th value is in the interval 11.25-11.75
Group of Q3 = 11.25-11.75
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (11.25 + ( 0.5/ 14)* (3* (60/4) – 36)
Q3 = 11.57
QD = (Q3 - Q1) / 2
QD = (11.57 – 10.58) / 2 = 0.495
Example 5 – Calculate quartile deviation from the following data
CI | F |
10 – 15 | 6 |
15 – 20 | 10 |
20 – 25 | 15 |
25 – 30 | 22 |
30 – 40 | 12 |
40 – 50 | 9 |
50 – 60 | 4 |
60 - 70 | 2 |
Solution:
CI | F | Cf |
10 – 15 | 6 | 6 |
15 – 20 | 10 | 16 |
20 – 25 | 15 | 31 |
25 – 30 | 22 | 53 |
30 – 35 | 12 | 65 |
35 – 40 | 9 | 74 |
45 – 50 | 4 | 78 |
55 – 60 | 2 | 80 |
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(80)/4]th observation
Q1 = 20th observation
So, 20th value is in the interval 20 - 25
Group of Q1 = 20 - 25
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (20 + ( 5/ 15)* (1* (80/4) – 16)
Q1 = 21.33
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (80) /4] th observation
Q3 = 60th observation
So, 60th value is in the interval 30 - 35
Group of Q3 = 30 - 35
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (30 + ( 5/ 12)* (3* (80/4) – 53)
Q3 = 32.91
QD = (Q3 - Q1) / 2
QD = (32.91 – 21.33) / 2 = 5.79
Merits
- It provide better result than range mode
- It is not affected by extreme values
Demerits
- It is completely dependent on central item
- All items are not taken onto consideration
The average of the absolute values of deviation from the mean, median or mode is called mean deviation. This method removes shortcoming of range and QD.
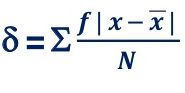
OR
 =
= 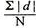
Where, ∑ is total of;
 X is the score, X is the mean, and N is the number of scores
X is the score, X is the mean, and N is the number of scores
D = Deviation of individual scores from mean
Example 1 –
Computation of mean deviation in ungrouped data
X = 55, 45, 39, 41, 40, 48, 42, 53, 41, 56
Solution:
X |
| Absolute deviation (signed ignored) |
55 | 55 - 46 = 9 | 9 |
45 | 45 – 46 = -1 | 1 |
39 | -7 | 7 |
41 | -5 | 5 |
40 | -6 | 6 |
48 | 2 | 2 |
42 | -4 | 4 |
53 | 7 | 7 |
41 | -5 | 5 |
56 | 10 | 10 |
∑X = 460 |
|
|
Mean = 460/10 = 46
MD = 56/10 = 5.6
Example 2- Peterdid a surveyed the number of pets owned by his classmates, with the following result. What is the mean deviation of the number of pets?
No. Of pets | Frequency |
0 | 4 |
1 | 12 |
2 | 8 |
3 | 2 |
4 | 1 |
5 | 2 |
6 | 1 |
Solution:
X | F | Fx |
|
|
0 | 4 | 0 | 1.8 | 7.2 |
1 | 12 | 12 | 0.8 | 9.6 |
2 | 8 | 16 | 0.2 | 1.6 |
3 | 2 | 6 | 1.2 | 2.4 |
4 | 1 | 4 | 2.2 | 2.2 |
5 | 2 | 10 | 3.2 | 6.4 |
6 | 1 | 6 | 3.2 | 4.2 |
| 30 | 54 | 4.2 | 33.6 |
Mean = 54/30 = 1.8
MD = 33.6/30 = 1.12
Computation of Mean deviation in grouped data
Example 3 -
Class interval | 15 – 19 | 20 – 24 | 25 – 29 | 30 – 34 | 35 – 39 | 40 – 44 | 45 - 49 |
Frequency | 1 | 4 | 6 | 9 | 5 | 3 | 2 |
Class Interval | F | X | FX | D | FD |
15 – 19 | 1 | 17 | 17 | 15 | 15 |
20 – 24 | 4 | 22 | 88 | 10 | 40 |
25 – 29 | 6 | 27 | 162 | 5 | 30 |
30 - 34 | 9 | 32 | 288 | 0 | 0 |
35 - 39 | 5 | 37 | 185 | 5 | 25 |
40 - 44 | 3 | 42 | 126 | 10 | 30 |
45 - 49 | 2 | 47 | 94 | 15 | 30 |
| N = 30 |
| ∑fx = 960 |
|  |
Mean =960/30 = 32
MD = 170 / 30 = 5.667
Coefficient of mean deviation
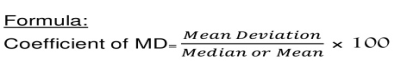
Coefficient of mean deviation = (5.67/32)*100 = 17.71
Example 4 – Calculate mean deviation from the median
Class | 5 -15 | 15 - 25 | 25 - 35 | 35 - 45 | 45 – 55 |
Frequency | 5 | 9 | 7 | 3 | 8 |
Solution:
x | f | Cf | Mid-point x | x –median | F(x-m) |
5 -15 | 5 | 5 | 10 | 17.42 | 87.1 |
15 -25 | 9 | 14 | 20 | 7.42 | 66.78 |
25 -35 | 7 | 21 | 30 | 2.58 | 18.06 |
35 -45 | 3 | 24 | 40 | 12.58 | 37.74 |
45- 55 | 8 | 32 | 50 | 22.58 | 180.64 |
| 32 |
|
|
| 390.32 |
Since n/2 = 32/2 = 16, therefore the class is 25 – 35 is the median.
Median = 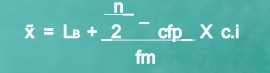
 Median = 25+16-14 *10 = 27.42
Median = 25+16-14 *10 = 27.42
7
MD from median is 390.32/32 = 12.91
Example 5 – calculate the mean deviation from continuous frequency distribution
Age group | 15 - 25 | 25 - 35 | 35 - 45 | 45 - 55 |
No. Of people | 25 | 54 | 34 | 20 |
Solution:
Age group (X) | Number of people (f) | Midpoint x | Fx |
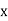 |
|
15 – 25 | 25 | 20 | 500 | 13.684 | 324.1 |
25 – 35 | 54 | 30 | 1620 | 3.684 | 198.936 |
35 – 45 | 34 | 40 | 1360 | 6.316 | 214.744 |
45 - 55 | 20 | 50 | 1000 | 16.316 | 352.32 |
| 133 |
|
|
| 1090.1 |
Mean = 4480/133 = 33.684
MD = 1090.1/133 = 8.196
Merits
- It is easy to calculate
- It helps in making comparison
- It is not affected by extreme items
Demerits
- It ignores algebraic sign. And are not used for mathematical treatment
- It is not reliable
Standard deviation is calculated as square root of average of squared deviations taken from actual mean. It is also called root mean square deviation. This measure suffers from less drawbacks and provides accurate results. It removes the drawbacks of ignoring algebraic sign. We square the deviation to make them positive.
Two ways of computing SD
- Direct method
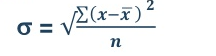
2. Shortcut method
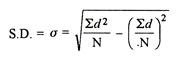
d = Deviation of the score from an assumed mean, say AM; i.e. d = (X – AM). AM is assumed mean
d2 = the square of the deviation.
∑d = the sum of the deviations.
∑d2 = the sum of the squared deviations.
N = No. Of the scores
Standard deviation in ungrouped data
- Direct method
Example 1–
X = 12, 15, 10, 8, 11, 13, 18, 10, 14, 9
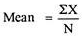
Mean = 120/10 = 12
Scores | d | 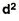 |
12 | 12-12 = 0 | 0 |
15 | 15-12 = 3 | 9 |
10 | 10 -12 = -2 | 4 |
8 | -4 | 16 |
11 | -1 | 1 |
13 | 1 | 1 |
18 | 6 | 36 |
10 | -2 | 4 |
14 | 2 | 4 |
9 | -3 | 9 |
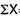 | 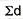 | 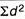 |
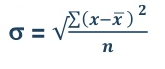
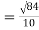 = 2.9
= 2.9
2. Shortcut method
Assumed mean (AM) = 11
Scores | D = (X- AM) | 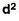 |
12 | 12-11 = 1 | 1 |
15 | 15-11 = 4 | 16 |
10 | 10 -11 = -1 | 1 |
8 | -3 | 9 |
11 | 0 | 0 |
13 | 2 | 4 |
18 | 7 | 49 |
10 | --1 | 1 |
14 | 3 | 9 |
9 | -2 | 4 |
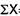 | 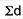 | 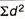 |
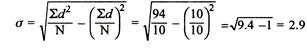
SD from short cut method = 2.9
Example 2 –Ram did a survey of the number of pets owned by his classmates, with the following results
No. Of pets | Frequency |
0 | 4 |
1 | 12 |
2 | 8 |
3 | 2 |
4 | 1 |
5 | 2 |
6 | 1 |
Solution:
x | f | Fx |
|
|
|
0 | 4 | 0 | -1.8 | 3.24 | 12.96 |
1 | 12 | 12 | -0.8 | 0.64 | 7.68 |
2 | 8 | 16 | 0.2 | 0.04 | 0.32 |
3 | 2 | 6 | 1.2 | 1.44 | 2.88 |
4 | 1 | 4 | 2.2 | 4.84 | 4.84 |
5 | 2 | 10 | 3.2 | 10.24 | 20.48 |
6 | 1 | 6 | 4.2 | 17.64 | 17.64 |
| 30 | 54 |
|
| 66.80 |
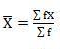
Mean = 54/30 = 1.8
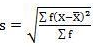
SD = √66.80/30 = 1.49
Standard deviation in grouped data
Direct method
Example 3 –
C.I. | 0 - 2 | 3 - 5 | 6- 8 | 9-11 | 12-14 | 15 -17 | 18 - 20 |
F | 1 | 3 | 5 | 7 | 6 | 5 | 3 |
Solution:
C.I | f | Mid-point x | Fx | d | 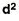 | Fd2 |
0-2 | 1 | 1 | 1 | -10.1 | 102.01 | 102.01 |
3-5 | 3 | 4 | 12 | -7.1 | 50.41 | 151.23 |
6-8 | 5 | 7 | 35 | -4.1 | 16.81 | 84.05 |
9-11 | 7 | 10 | 70 | -1.1 | 1.21 | 8.47 |
12-14 | 6 | 13 | 78 | 1.9 | 3.61 | 21.66 |
15-17 | 5 | 16 | 80 | 4.9 | 24.01 | 120.05 |
18-20 | 3 | 19 | 57 | 7.9 | 62.41 | 187.23 |
| 30 |
| 333 |
|
| 674.70 |
Mean = 333/30 = 11.1
SD =
= 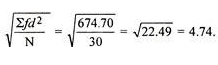
Shortcut method
C.I | f | Mid-point x | d(X-AM) | Fd | Fd2 |
0-2 | 1 | 1 | -9 | -9 | 81 |
3-5 | 3 | 4 | -6 | -18 | 108 |
6-8 | 5 | 7 | -3 | -15 | 45 |
9-11 | 7 | 10 | 0 | 0 | 0 |
12-14 | 6 | 13 | 3 | 18 | 54 |
15-17 | 5 | 16 | 6 | 30 | 180 |
18-20 | 3 | 19 | 9 | 27 | 243 |
| 30 |
|
| 33 | 711 |
Assumed mean = 10
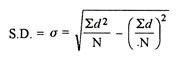
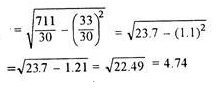
Step deviation method
C.I | f | Mid-point x | d | Fd | Fd2 |
0-2 | 1 | 1 | -3 | -3 | 9 |
3-5 | 3 | 4 | -2 | -6 | 12 |
6-8 | 5 | 7 | -1 | -5 | 5 |
9-11 | 7 | 10 | 0 | 0 | 0 |
12-14 | 6 | 13 | 1 | 6 | 6 |
15-17 | 5 | 16 | 2 | 10 | 20 |
18-20 | 3 | 19 | 3 | 9 | 27 |
| 30 |
|
| 11 | 79 |
Here, d is calculated as (X –AM)/i, where i is length of class interval
d = (1 -10)/3 = -3 and so on
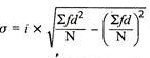
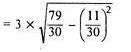
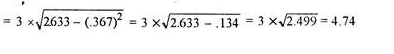
Coefficient of standard deviation
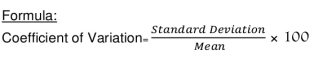
Coefficient of SD = (4.74/11.1)*100 = 42.70
Example 4 – calculate the standard deviation using the direct method
Class interval | Frequency |
30 – 39 | 3 |
40 – 49 | 1 |
50 – 59 | 8 |
60 – 69 | 10 |
70 – 79 | 7 |
80 – 89 | 7 |
90 – 99 | 4 |
Solution:
Class interval | Frequency | Mid-point x | Fx |
|
|
|
30 – 39 | 3 | 34.5 | 103.5 | -33.5 | 1122.25 | 3366.75 |
40 – 49 | 1 | 44.5 | 44.5 | -23.5 | 552.25 | 552.25 |
50 – 59 | 8 | 54.5 | 436.0 | -13.5 | 182.25 | 1458 |
60 – 69 | 10 | 64.5 | 645.0 | -3.5 | 12.25 | 122.5 |
70 – 79 | 7 | 74.5 | 521.5 | 6.5 | 42.25 | 295.75 |
80 – 89 | 7 | 84.5 | 591.5 | 16.5 | 272.25 | 1905.75 |
90 – 99 | 4 | 94.5 | 378.0 | 26.5 | 702.25 | 2809 |
| 40 |
| 2720 |
|
| 10510 |
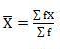
Mean = 2720/40 = 68
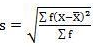
SD = √10510/40 = 16.20
Example 5 - calculate the mean and standard deviation of hours spent watching television by the 220 students.
Hours | No. Of students |
10 – 14 | 2 |
15 – 19 | 12 |
20 – 24 | 23 |
25 – 29 | 60 |
30 – 34 | 77 |
35 – 39 | 38 |
40 - 44 | 8 |
Solution:
Hours | No. Of students | x | Fx |
|
|
|
10 – 14 | 2 | 12 | 24 | -17.82 | 317.49 | 634.98 |
15 – 19 | 12 | 17 | 204 | -12.82 | 164.31 | 1971.67 |
20 – 24 | 23 | 22 | 506 | -7.82 | 61.12 | 1405.85 |
25 – 29 | 60 | 27 | 1620 | -2.82 | 7.94 | 476.53 |
30 – 34 | 77 | 32 | 2464 | 2.18 | 4.76 | 366.55 |
35 – 39 | 38 | 37 | 1406 | 7.18 | 51.58 | 1959.98 |
40 - 44 | 8 | 42 | 336 | 12.18 | 148.40 | 1187.17 |
| 220 |
| 6560 |
|
| 8002.73 |
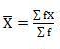
Mean = 6560/220 = 29.82
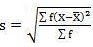
SD = √8002.73/220 = 6.03
Merits
- It takes into account all the items and are used for future statistical analysis
- It is suitable for making comparison
Demerits
- It is difficult to compute
Standard Variation is an absolute measure of dispersion. When comparison between two series has to be made, coefficient of variation is used. Coefficient of variation is a statistical measure of the dispersion of data with respect to mean.

Where, σ = Standard Deviation
µ = Mean
Example 1: Calculate Coefficient of Variation from the following data given below:
Standard Deviation = 4.5 Mean= 12.
Solution: We know,
Coefficient of Variation =  x 100%
x 100%
= 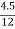 x 100%
x 100%
= 37.5%
Example 2: Calculate Standard Deviation and Co-efficient of Variation.
:
Class interval | Frequency |
30 – 39 | 3 |
40 – 49 | 1 |
50 – 59 | 8 |
60 – 69 | 10 |
70 – 79 | 7 |
80 – 89 | 7 |
90 – 99 | 4 |
Solution:
Class interval | Frequency | Mid-point x | Fx |
|
|
|
30 – 39 | 3 | 34.5 | 103.5 | -33.5 | 1122.25 | 3366.75 |
40 – 49 | 1 | 44.5 | 44.5 | -23.5 | 552.25 | 552.25 |
50 – 59 | 8 | 54.5 | 436.0 | -13.5 | 182.25 | 1458 |
60 – 69 | 10 | 64.5 | 645.0 | -3.5 | 12.25 | 122.5 |
70 – 79 | 7 | 74.5 | 521.5 | 6.5 | 42.25 | 295.75 |
80 – 89 | 7 | 84.5 | 591.5 | 16.5 | 272.25 | 1905.75 |
90 – 99 | 4 | 94.5 | 378.0 | 26.5 | 702.25 | 2809 |
| 40 |
| 2720 |
|
| 10510 |
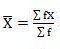
Mean = 2720/40 = 68
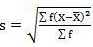
SD = √10510/40 = 16.20
Coefficient of Variation =  x 100%
x 100%
= 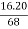 x 100%
x 100%
= 23.82 %
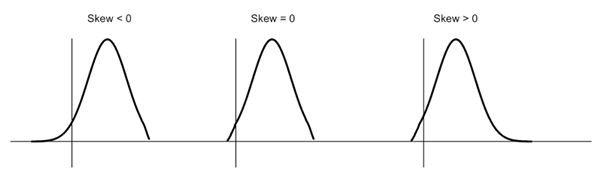
Skewness is a measure of symmetry or lack of symmetry in a distribution. A distribution is symmetric if it looks same both its left and right side. The skewness for normal distribution is Zero. Negative values for skewness indicate that the data are skewed left and positive values for skewness indicate that the data are skewed right. For small data sets, this measure is unreliable. The below diagram shows how a normal distribution curve looks like in different situation of skewness:
The formula for measuring Coefficient of Skewness as given by Karl Pearson is as under:
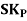 =
= 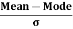
Where, 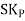 = Karl Pearson’s Coefficient of Skewness
= Karl Pearson’s Coefficient of Skewness
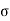 = Standard Deviation
= Standard Deviation
The formula for measuring Co-efficient of Skewness as given by Bowley is as under:
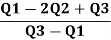
Example 1: From the following data, calculate Karl Pearson’s Co-efficient of Skewness:
Mean = 16, Mode = 38, Standard Deviation = 5
Solution: We know that
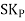 =
= 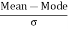
= 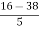
= -4.4
Example 2 – Below are the data of hours spent watching television by the 220 students. CalculateKarl Pearson’s Co-efficient of Skewness.
Hours | No. Of students |
10 – 14 | 2 |
15 – 19 | 12 |
20 – 24 | 23 |
25 – 29 | 60 |
30 – 34 | 77 |
35 – 39 | 38 |
40 - 44 | 8 |
Solution:
Hours | No. Of students | x | Fx |
|
|
|
10 – 14 | 2 | 12 | 24 | -17.82 | 317.49 | 634.98 |
15 – 19 | 12 | 17 | 204 | -12.82 | 164.31 | 1971.67 |
20 – 24 | 23 | 22 | 506 | -7.82 | 61.12 | 1405.85 |
25 – 29 | 60 | 27 | 1620 | -2.82 | 7.94 | 476.53 |
30 – 34 | 77 | 32 | 2464 | 2.18 | 4.76 | 366.55 |
35 – 39 | 38 | 37 | 1406 | 7.18 | 51.58 | 1959.98 |
40 - 44 | 8 | 42 | 336 | 12.18 | 148.40 | 1187.17 |
| 220 |
| 6560 |
|
| 8002.73 |
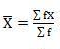
Mean = 6560/220 = 29.82
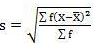
SD = √8002.73/220 = 6.03
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
Here modal class is 30 – 34 (Since the frequency is highest)
L1 = 30, L2 = 34, d1 = 17, d2 = 39
 Mode = 30 + (34 – 30) 17
Mode = 30 + (34 – 30) 17
17 + 39
Mode = 30 + 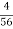 x 17
x 17
= 30 + 1.21
= 31.21
Therefore, Co-efficient of Skewness
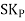 =
= 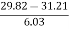
= 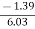
= - 0.23
Example 3: Calculate Bowley’s Coefficient of Skewness from the following test scores:
Sl. N o | Test scores |
1 | 17 |
2 | 17 |
3 | 26 |
4 | 27 |
5 | 30 |
6 | 30 |
7 | 31 |
8 | 37 |
Solution:
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (8 + 1) /4] th observation
Q1 = 2.25 th observation
Thus, 2.25 th observation lies between the 2nd and 3rd value in the ordered group, between frequency 17 and 26
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 17 + 0.75 * (26 – 17) = 23.75
Second quartile(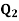 )
)
Q2= [2 * (8 + 1) /4] th observation
Q2 = 4.5th Observation
So, 4.5th observation lies between 4th and 5th value in ordered group, between frequency 27 and 30.
Hence Q2 = 4th observation + 0.50 * (5th observation – 6th observation)
Q2 = 27 + 0.50 * (30 – 27) = 28.5
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (8 + 1) /4] th observation
Q3 = 6.75 th observation
So, 6.75 th observation lies between the 6th and 7th value in the ordered group, between frequency 30 and 31
Third quartile (Q3) is calculated as
Q3 = 6th observation +0.25 * (7th observation – 6th observation)
Q3 = 30 + 0.25 * (31 – 30) = 30.25
Therefore, Bowley’s Coefficient of Skewness is calculated as under:
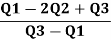
= 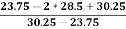
= 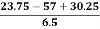 = - 0.461
= - 0.461
References:
- B.N Gupta – Statistics
- S.P Singh – statistics
- Gupta and Kapoor – Statistics
- Yule and Kendall – Statistics method






















