Unit 3

Hypothesis: A Test of Significance

3.1 (A) Hypothesis concept and Sources of hypothesis

The hypothesis is an assumption based on some evidence. This is the initial point of any investigation that translates a prediction into the research questions. This involves elements such as variables, population and the relationship between the variables. A hypothesis for research is a hypothesis used to test the relationship between two or more variables.

Characteristics of Hypothesis

Following are the characteristics of hypothesis:

• To consider it to be reliable, the hypothesis should be clear and precise.
• If the hypothesis is a relational hypothesis, then the relationship between variables should be stated.
• The hypothesis must be specific and should have scope for more tests to be performed.
• The way the hypothesis is explained must be very simple and it should also be understood that the hypothesis's simplicity is not related to its significance.

Sources of Hypothesis

• The similarity between phenomena.
• Observations from past research, present-day experiences and from rivals.
• Scientific ideas.
• General patterns that affect people's thinking process.

3.2 Procedure for formulation of hypothesis

An analyst tests a statistical sample in hypothesis testing, with the aim of providing evidence about the plausibility of the null hypothesis.

By measuring and examining a random sample of the population that is being analysed, statistical analysts test a hypothesis. A random population sample is used by all analysts to test two separate hypotheses: the null hypothesis and the alternative hypothesis.

The null hypothesis is usually a population parameter equality hypothesis; e.g., a null hypothesis may state that the mean return of the population is equal to zero. The opposite of a null hypothesis is effectively the alternative hypothesis (e.g., the population mean return is not equal to zero). They are mutually exclusive, therefore, and only one can be true. One of the two hypotheses will always be true, however.

4 Steps of Testing of Hypotheses

A four-step process is used to test all hypotheses:

1. The first step is to state the two hypotheses for the analyst so that only one can be correct.

2. The next step is to formulate an analysis plan that outlines how to evaluate the information.

3. The third step is to execute the plan and to analyse the sample data physically.

4. The fourth and final step is to analyse the findings and either dismiss the null hypothesis or, given the data, state that the null hypothesis is plausible.

Real-world instance

If, for example, a person wants to test that a penny has exactly a 50 percent chance of landing on heads, the null hypothesis would be that 50 percent is correct, and the alternative hypothesis would be that 50 percent is not correct.

Mathematically, the null hypothesis would be represented as Ho: P = 0.5. The alternative hypothesis would be denoted as "Ha" and be identical to the null hypothesis, except with the equal sign struck-through, meaning that it does not equal 50 percent.

It takes a random sample of 100-coin flips, and then tests the null hypothesis. The analyst would assume that a penny does not have a 50 percent chance of landing on heads if it is found that the 100-coin flips were distributed as 40 heads and 60 tails, and would reject the null hypothesis and accept the alternative hypothesis.

If, on the other hand, 48 heads and 52 tails were present, then it is plausible that the coin might be fair and still produce such an outcome. The analyst states that the difference between the expected results (50 heads and 50 tails) and the observed results (48 heads and 52 tails) is "explainable by chance alone" in cases such as this where the null hypothesis is "accepted."

3.3 Types of hypothesis

• Simple hypothesis
• Complex hypothesis
• Directional hypothesis
• Non-directional hypothesis
• Null hypothesis
• Associative and casual hypothesis

Simple Hypothesis

The similarity between phenomena.

Observations from past research, present-day experiences and from rivals.

Scientific ideas.

General patterns that affect people's thinking process.

Complex Hypothesis

This shows the relationship between two or more variables that are dependent and two or more variables that are independent. Eating more vegetables and fruits results in weight loss, glowing skin, reducing the risk of many diseases such as heart disease, high blood pressure, and certain cancers.

Directional Hypothesis

This demonstrates how a researcher is intellectual and committed to a specific result. Its nature can also be predicted by the relationship between variables. Children aged four years who eat proper food over a five-year period, for example, have higher IQ levels than children who do not eat proper food. This indicates the effect and direction of the impact.

Non-directional Hypothesis

It is used when it does not involve any theory. It is a statement that there is a relationship between two variables, without predicting the relationship's exact nature (direction).

Null Hypothesis

It provides a declaration contrary to the hypothesis. It's a negative statement, and independent and dependent variables do not have a relationship. The symbol is denoted by the word "HO".

Associative and Causal Hypothesis

An associative hypothesis occurs when one variable changes, resulting in a change in the other variable. The causal hypothesis, however, proposes an interaction of cause and effect between two or more variables.

Examples of Hypothesis

Following are the examples of hypothesis based on their types:

• An example of a simple hypothesis is the consumption of sugar drinks every day that leads to obesity.
• An example of a null hypothesis is that all lilies have the same number of petals.
• If a person gets 7 hours of sleep, then less fatigue will be felt than if he sleeps less.

Functions of Hypothesis

• The hypothesis helps to enable observation and experiments.
• This will be the starting point for the investigation.
• Hypothesis assists in the observation’s verification.
• It helps to guide inquiries in the correct direction.
• Researchers use hypothesis to put down their thoughts directing how the experiment would take place. Following are the steps that are involved in the scientific method:
  • Formation of question
  • Doing background research
  • Creation of hypothesis
  • Designing an experiment
  • Collection of data
  • Result analysis
  • Summarizing the experiment
  • Communicating the results

3.4 (B) Test of significance in large sample

Test of Significance of difference for Large Samples (Z test)

(I)                Hypothesis Testing for Single Population Mean

Two-Tailed Test: Let 𝜇 be the hypothesized value of the population mean to be tested. For this the null and alternative hypotheses for two tailed-tests are defined as:

H0:  = 𝑋̅ or  − 𝑋̅ =0

H1:  ≠ 𝑋̅

And;

If standard deviation 𝜎 of the population is known, then based on the central limit theorem, the sampling distribution of mean 𝑥̅ would follow the standard normal distribution for a large sample size. Then z-test statistic is given by; Test-statistic: z = 𝑥̅− 𝜎/√n

Or z = 𝑥̅− 𝑆.𝐸.

Here S.E. Stands for Standard Error of Mean = 𝜎 √𝑛 ̅̅̅̅

If the population standard deviation 𝞂 is not known, then a sample standard deviation ‘s’ is used to estimate 𝞂. The value of the z-test statistic is given by;

z = 𝑥̅− 𝑠/√−𝑛

The decision on the basis of critical value and calculated value for the two-tailed test can be presented in the following form:

• Reject 𝐻0 if 𝑧𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒𝑑 ≤ -𝑧/2 or 𝑧𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒𝑑  𝑧/2 i.e., Null Hypothesis is rejected if calculated value is less than (-) critical value or greater than (+) critical value in case of two tailed test.
• Accept 𝐻0 if −𝑧/2  z Calculated  𝑧/2 Where 𝑧/2 is the table value (also called Critical Value) of z at a chosen level of significance i.e.,.

Left-Tailed Test: Large sample (n>30) hypothesis testing about a population mean for a left-tailed test is of the form;

• Null Hypothesis (𝐻0):   𝑥̅and 𝐻𝑎:  𝑥̅

Test-statistic: z = 𝑥̅− 𝜎/√𝑛

Decision rule:

• Reject 𝐻0 if 𝑧𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒𝑑 ≤ -𝑧 (Table value of z at )

Right-Tailed Test: Large sample (n>30) hypothesis testing about a population mean for a left-tailed test is of the form;

𝐻0:   𝑥̅ and 𝐻1:  > 𝑥̅(Right-tailed test)

Test-statistic: z = 𝑥̅− 𝜎/√n

Decision rule:

Reject 𝐻0 if 𝑧𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒𝑑  𝑧 (Table value of z at )

Accept 𝐻0 if 𝑧𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒𝑑 𝑧

Illustration 1: A company producing fluorescent light bulbs claims that the average life of the bulbs is 1570 hours. The mean life time of sample of 200 fluorescent light bulbs was found to be 1600 hours with a standard deviation of 150 hours. Test for the company at 1% level of significance, whether the claim that the average life of the bulbs is 1570 hours is acceptable.

Solution: Let us take the null hypothesis that mean life time of bulbs is 1570 hours,

i.e., 𝐻0: 𝑋̅ =  and 𝐻1: 𝑋̅ ≠ (Two- tailed test)

Given: n= 200, 𝑥̅= 1600 hours, s = 150 hours, and  = 0.01. Thus, using the z test statistic;

z = 𝑥̅− 𝑠/√𝑛 = 1600−1570 150/√200 = 30 150/14.14 = 10.60

Since the calculated value 𝑧𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒𝑑 = 10.60 which is more than its critical value 𝑧 = 2.58, the 𝐻0 is rejected. Hence, we conclude that the mean life time of bulbs produced by the company is not 1570 hours. In other words, the difference between sample means and universe Mean is significant, i.e.: 𝑋̅ ≠

Test of Hypothesis for the Difference between Two Population Means

If two random samples with ̅𝑋1, 𝜎1, 𝑛1, and 𝑋̅ 2, 𝜎2, 𝑛2 are drawn from different populations, then the Z statistic takes the following form:

Z= 𝑋̅1−𝑋̅2 √ 𝜎1 2 𝑛1 + 𝜎2 2 𝑛2

Illustration 2: A potential buyer wants to decide which of the two brands of electric bulbs he should buy as he has to buy them in bulk. As a specimen, he buys 200 bulbs of each of the two brands –A and B. On using these bulbs, he finds that brand A has a mean life of 1,400 hours with a standard deviation of 60 hours and brand B has mean life of 1,250 hours with a standard deviation of 50 hours. Do the two brands differ significantly in quality? Use =0.05.

Solution: Let us take the null hypothesis that the two brands do not differ significantly in quality:

𝐻0: 1 = 2 𝐻𝑎: 1 ≠  2 (Two-tailed test)

Where 1 = Mean life of Brand A bulbs, and  2 = mean life of brand B bulbs. We now construct the Z statistic.

Z= 𝑋̅1−𝑋̅2 √ 𝜎1 2 𝑛1 + 𝜎2 2 𝑛2 = 1400−1250 √ (60) 2 200 + (50) 2 200 = 150 √ 3600 200 + 2500 200 = 150 √18+12.5

= 150 √30.5 = 150 5.52 = 27.17

As we are given at =0.05, the value of Z for a two- tailed test is 1.96. Since the calculated value of Z (27.17) falls in the rejection region, we reject the null hypothesis and, therefore, conclude that the bulbs of two brands differ significantly in quality.

3.5 Standard error

Standard error is the standard deviation of sampling distribution of a statistic (S.E) and is considered the key to sampling theory. The utility of the concept of standard error in statistical induction arises on account of the following reasons.

The standard error helps in testing whether the difference between observed and expected frequencies could arise due to chance. The criterion usually adopted is that if a difference is less than 3 times the S.E., the difference is supposed to exist as a matter of chance and if the difference is equal to or more than 3 times the S.E., chance fails to account for it, and we conclude the difference as significant difference. This criterion is based on the fact that at X ± 3 (S.E.) the normal curve covers an area of 99.73 per cent. Sometimes the criterion of 2 S.E. Is also used in place of 3 S.E. Thus, the standard error is an important measure in significance tests or in examining hypotheses. If the estimated parameter differs from the calculated statistic by more than 1.96 times the S.E., the difference is taken as significant at 5 per cent level of significance. This, in other words, means that the difference is outside the limits i.e., it lies in the 5 per cent area (2.5 per cent on both sides) outside the 95 per cent area of the sampling distribution. Hence, we can say with 95 per cent confidence that the said difference is not due to fluctuations of sampling. In such a situation our hypothesis that there is no difference is rejected at 5 per cent level of significance. But if the difference is less than 1.96 times the S.E., then it is considered not significant at 5 per cent level and we can say with 95 per cent confidence that it is because of the fluctuations of sampling. In such a situation our null hypothesis stands true. 1.96 is the critical value at 5 per cent level. The product of the critical value at a certain level of significance and the S.E. Is often described as ‘Sampling Error’ at that particular level of significance. We can test the difference at certain other levels of significance as well depending upon our requirement. The following table gives some idea about the criteria at various levels for judging the significance of the difference between observed and expected values:

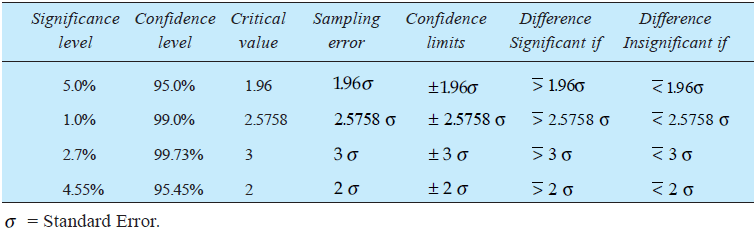
1.   The standard error gives an idea about the reliability and precision of a sample. The smaller the S.E., the greater the uniformity of sampling distribution and hence, greater is the reliability of sample. Conversely, the greater the S.E., the greater the difference between observed and expected frequencies. In such a situation the unreliability of the sample is greater. The size of S.E., depends upon the sample size to a great extent and it varies inversely with the size of the sample. If double reliability is required i.e., reducing S.E. To 1/2 of its existing magnitude, the sample size should be increased four-fold.
2.   The standard error enables us to specify the limits within which the parameters of the population are expected to lie with a specified degree of confidence. Such an interval is usually known as confidence interval. The following table gives the percentage of samples having their mean values within a range of population mean.

3.6 Difference of mean test of significance in small T test, F test and Z test

A t-test is a statistical test that is used to compare the means of two groups. It is often used in hypothesis testing to determine whether a process or treatment actually has an effect on the population of interest, or whether two groups are different from one another.

When to use a t-test

A t-test can only be used when comparing the means of two groups (a.k.a. Pairwise comparison). If you want to compare more than two groups, or if you want to do multiple pairwise comparisons, use an ANOVA test or a post-hoc test.

The t-test is a parametric test of difference, meaning that it makes the same assumptions about your data as other parametric tests. The t-test assumes your data:

1. Are independent
2. Are (approximately) normally distributed.
3. Have a similar amount of variance within each group being compared (a.k.a. Homogeneity of variance)

If your data do not fit these assumptions, you can try a nonparametric alternative to the t-test, such as the Wilcoxon Signed-Rank test for data with unequal variances.

What type of t-test should I use?

When choosing a t-test, you will need to consider two things: whether the groups being compared come from a single population or two different populations, and whether you want to test the difference in a specific direction.

One-sample, two-sample, or paired t-test?

• If the groups come from a single population (e.g., measuring before and after an experimental treatment), perform a paired t-test.
• If the groups come from two different populations (e.g., two different species, or people from two separate cities), perform a two-sample t-test (a.k.a. independent t-test).
• If there is one group being compared against a standard value (e.g., comparing the acidity of a liquid to a neutral pH of 7), perform a one-sample t-test.

One-tailed or two-tailed t-test?

• If you only care whether the two populations are different from one another, perform a two-tailed t-test.
• If you want to know whether one population mean is greater than or less than the other, perform a one-tailed t-test.

An F-test is a type of statistical test that is very flexible. You can use them in a wide variety of settings. F-tests can evaluate multiple model terms simultaneously, which allows them to compare the fits of different linear models. In contrast, t-tests can evaluate just one term at a time.

To calculate the F-test of overall significance, your statistical software just needs to include the proper terms in the two models that it compares. The overall F-test compares the model that you specify to the model with no independent variables. This type of model is also known as an intercept-only model.

The F-test for overall significance has the following two hypotheses:

• The null hypothesis states that the model with no independent variables fits the data as well as your model.
• The alternative hypothesis says that your model fits the data better than the intercept-only model.

In statistical output, you can find the overall F-test in the ANOVA table. An example is below.

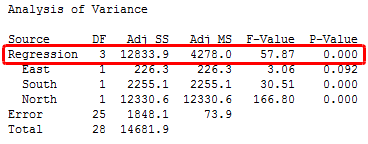
Interpreting the Overall F-test of Significance

Compare the p-value for the F-test to your significance level. If the p-value is less than the significance level, your sample data provide sufficient evidence to conclude that your regression model fits the data better than the model with no independent variables.

This finding is good news because it means that the independent variables in your model improve the fit!

Generally speaking, if none of your independent variables are statistically significant, the overall F-test is also not statistically significant. Occasionally, the tests can produce conflicting results. This disagreement can occur because the F-test of overall significance assesses all of the coefficients jointly whereas the t-test for each coefficient examines them individually. For example, the overall F-test can find that the coefficients are significant jointly while the t-tests can fail to find significance individually.

These conflicting test results can be hard to understand, but think about it this way. The F-test sums the predictive power of all independent variables and determines that it is unlikely that all of the coefficients equal zero. However, it’s possible that each variable isn’t predictive enough on its own to be statistically significant. In other words, your sample provides sufficient evidence to conclude that your model is significant, but not enough to conclude that any individual variable is significant.

Z test

A z-test is a statistical test used when the variances are known and the sample size is large to determine whether two population meanings are different. The test statistics are assumed to have a normal distribution, and for an accurate z-test to be performed, nuisance parameters such as standard deviation should be known.

A z-statistic, or z-score, is a number representing how many standard deviations a score derived from a z-test is above or below the mean population.

• A z-test is a statistical test to determine if when the variances are known and the sample size is large, two population meanings are different.
• It can be used for testing hypotheses in which a normal distribution follows the z-test.
• A z-statistic, or z-score, is a number that represents the z-test outcome.
• Z-tests are closely related to t-tests, but when an experiment has a small sample size, t-tests are best conducted.
• T-tests also assume that the standard deviation is unknown, whereas z-tests presume that it is known.

How Z-Tests Work

A one-sample location test, a two-sample location test, a paired difference test, and a maximum likelihood estimate are examples of tests that can be conducted as z-tests. Z-tests are closely related to t-tests, but when an experiment has a small sample size, t-tests are best conducted. T-tests also presume that the standard deviation is unknown, whereas z-tests presume that it is known. The assumption of the sample variance equalling the population variance is made if the standard deviation of the population is unknown.

Hypothesis Test

The z-test is also a test of hypotheses in which a normal distribution follows the z-statistic. For greater-than-30 samples, the z-test is best used because, under the central limit theorem, the samples are considered to be approximately normally distributed as the number of samples gets larger. The null and alternative hypotheses, alpha and z-score, should be stated when conducting a z-test. Next, it is necessary to calculate the test statistics and state the results and conclusions.

One-Sample Z-Example Test

Assume that an investor wishes to test whether a stock's average daily return is greater than 1%. It calculates a simple random sample of 50 returns and has an average of 2 percent. Assume that the standard return deviation is 2.5 percent. The null hypothesis, therefore, is when the average, or mean, equals 3%.

The alternative hypothesis, on the other hand, is whether the average return is greater than 3% or less. Assume an alpha is selected with a two-tailed test of 0.05 percent. Therefore, in each tail, there is 0.025 percent of the samples, and the alpha has a critical value of 1.96 or -1.96. The null hypothesis is rejected if the value of z is greater than 1.96 or less than -1.96.

The z-value is calculated by subtracting from the observed average of the samples the value of the average daily return selected for the test, or 1 percent in this case. Next, divide the resulting value by the standard deviation of the number of values observed, divided by the square root. It is therefore calculated that the test statistic is 2.83, or (0.02 - 0.01) / (0.025 / (50) ^ (1/2)). Since z is greater than 1.96, the investor rejects the null hypothesis and concludes that the average daily return is greater than 1 percent.

References:

1. Research for Marketing Decisions Paul E. Green, Donald S. Tull
2. Marketing Research- Text and Cases Harper W. Boyd Jr. , Ralph Westfall.
3. Research methodology in Social sciences, O.R.Krishnaswamy, Himalaya Publication