UNIT 1
Introduction of Engineering Graphics
- Engineering drawing is any kind of drawing that communicates an idea, concept, or design. There are many types of engineering drawings, and each type has its own set of rules, standards, and conventions. The aim of this project is to create a set of learning modules to introduce students from all engineering disciplines to the basic concepts and the use of engineering drawings in the design, construction, manufacturing, and maintenance fields. In these modules, students will learn the basic knowledge and skills in engineering drawings concepts, develop the capability to read and interpret blue prints, and gain an understanding of 2D, 3D, and Building Information Modelling (BIM) formats of engineering drawings.
- These modules could be used for inverted delivery of an introductory engineering design course or for the hybrid delivery of engineering drawing content in a set of courses. We envision these modules partially or fully replacing in-person lectures and being paired with in-person experiential learning activities, such as design studios and hands-on exercises with real drawings, to create an effective and active learning experience. These modules could also be used to support a fully online course approach that could pair them with online discussions, synchronous chats, and other learning support tools.
To record information on paper (or another surface), instruments and equipment are required. Even for drawings made freehand, pencils, erasers, and sometimes coordinate paper or other special items are used. The lines made on drawings are straight or curved (including circles and arcs). They are made with drawing instruments, which are the necessary tools for laying down lines on a drawing in an accurate and efficient manner. To position the lines, a measuring device, a scale, is needed.
The various instruments will be described in detail later, but the opening of this chapter will serve as an introduction. To draw straight lines, the T square, with its straight blade and perpendicular head, or a triangle is used to support the stroke of the pencil. To draw circles, a compass is needed. In addition to the compass, the draftsman needs dividers for spacing distances and a small bow compass for drawing small circles. To draw curved lines other than circles, a French curve is required. A scale is used for making measurements.
- Drawing Paper
Drawing paper is made up of variety of qualities and manufactured in sheets or rolls. White drawing papers that will not turn yellow with age or exposure are used for finished drawings, maps, charts, and drawings for photographic reproduction. For pencil layouts and working drawings buff detail papers are preferred as they are easier on the eyes compared to white papers.
|
- Tracing Paper
Tracing papers are thin papers, natural or transparent, on which drawings are traced, in pencil or ink, and from which blueprints or similar contact prints can be made. In most drafting rooms original drawings are penciled on tracing papers, and blueprints are made directly from these drawings, a practice increasingly successful because of improvements both in papers and in printing.
- Thumbtacks
The best thumbtacks are made with thin heads and steel points screwed into them. Cheaper ones are made by stamping. Use tacks with tapering pins of small diameter and avoid flat-headed (often colored) map pins, as the heads are too thick and the pins rather large.
|
- Pencils
The basic instrument is the graphite lead pencil, made in various hardness’s. Each manufacturer has special methods of processing design to make the lead strong and yet give a smooth clear line.
|
In the left there is an ordinary pencil, with the lead set in wood and the other is a semi-automatic pencil with thinner leads. Both are fine but have the disadvantage that in use, the wood must be cut away to expose the lead (a time-consuming job), and the pencil becomes shorter and shorter until the last portion of it is to be discarded. Whereas semiautomatic pencils, with a chuck to clamp and hold the lead, are more convenient, has a plastic handle and changeable tip (for indicating the grade of lead).
Drawing pencils are graded by numbers and letters from 6B which is very soft and black, to 5B, 4B, 3B, 2B, B, and HB to F, the medium grade; then H, 2H, 3H, 4H, 5H, 6H, 7H, and 8H to 9H, the hardest. The soft (B) grades are used primarily for sketching and rendered drawings and the hard (H) grades for instrument drawings.
- Pencil Pointer
After the wood of the ordinary pencil is cut away with a pocketknife or mechanical sharpener, the lead must be formed to a long, conic point.
A pencil pointer is a tool for sharpening a pencil’s writing point by shaving away its worn surface.’=
|
- Erasers
The Ruby pencil eraser, large size with beveled ends, is the standard. This eraser not only removes pencil lines effectively but is better for ink, as it removes ink without seriously damaging the surface of paper or cloth.
Art gum or a soft-rubber eraser, is useful for cleaning paper and cloth of finger marks and smears that spoil the appearance of the completed drawing.
- Penholders and Pens
The penholder should have a grip of medium size, small enough to enter the mouth of a drawing-inkbottle easily yet not so small as to cramp the fingers while in use. A size slightly larger than the diameter of a pencil is good.
- Triangles
Triangles, are made of transparent hard or other plastic material. Through internal strains they sometimes lose their accuracy. Triangles should be kept flat to prevent warping. For ordinary work, a 6- or 8-in. 45° and a 10-in. 30-60° are good sizes.
|
- The T Squares
The fixed-head T square, is used for all ordinary work. It should be of hardwood, and the blade should be perfectly straight. The transparent-edged blade is much the best. A draftsman will have severalfixed-head squares of different lengths and will findan adjustable-head square of occasional use.
|
- Scales
Scales, are made in various number of graduations to meet the requirements of many kinds of work. For convenience, scales are classified according to their most-common uses.
Mechanical Engineer’s Scale
These are divided and numbered in such a way that fractions of inches represent inches. The most common ranges are 1/8, 1/4, 1/2, and 1 in. to the inch. These scales are known as the size scales because the reduced size also represents the ratio of size, as for example one-eighth size.
Mechanical engineer's scales are almost always "full divided"; that is, the smallest divisions run throughout the entire length.
They are generally graduated with the marked divisions numbered from right to left, as well as from left to right, as shown in Figure Mechanical engineer's scales are used mostly for drawings of machine parts and small structures where the drawing size is more than one-eighth the size of the actual object.
|
Civil Engineer’s Scale
These are divided into decimals with divisions ranging from 10, 20, 30, 40, 50, 60, and 80 to the inch. Such a scale is usually full divided and is sometimes numbered both from left to right and right to left. Civil engineer's scales are most used for plotting and drawing maps, although they are convenient for any work where divisions of the inch in tenths is required.
|
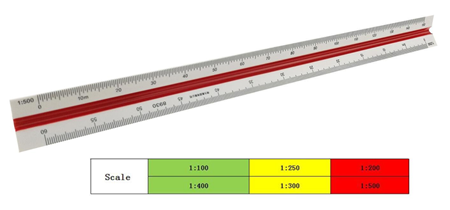
Metric Scales
Metric scales are supplied in all the styles and sizes and materials of other scales. They are usually full-divided and are numbered in meters, centimeters, or millimetres depending upon the reduction in size. Typical size reductions are: 1:1, 1:2, 1:5, 1:10, 1:20, 1:25, 1:33.3, 1:50, 1:75, 1:80, 1: 100, 1: 150. Also available are metric equivalent scales for direct conversion of English scales.
|
- Curves
Curve rulers, called "irregular curves" or "French curves," are used to draw curved lines other than circular arcs. The patterns for these curves are laid out in parts of ellipse and spirals or other mathematical curves in various combinations. For the student, one ellipse curve of the general shape or one spiral, either a logarithmic spiral is a useful small curve.
|
- Case Instruments
We have so far, except for curves considered only the instruments needed for drawing straight lines. A major portion of any drawing is likely to be circles and circle arcs, and the so called “case” instruments are used for these.
Divider:
It is used for laying off or transferring measurements.
|
Next is the large compass with lengthening bar and pen attachment. The three “bow” instruments are for smaller work. They are almost always made without the conversion feature.
|
The ruling pen is used for inking straight lines.
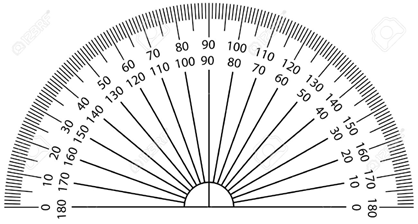
Protractor is used to measure angles upto 180°.
|
- Cautions in the use of Instruments
- Scales are not to be used as a ruler for drawing lines.
- Horizontal lines with the lower edge should not be drawn with a T square.
- The lower edge of T square should not be used as a base for drawing triangles.
- T square is not to be used as hammer.
- Never put either end of a pencil into the mouth.
- Never sharpen a pencil over a drawing board.
- Never oil the joints of compasses.
- Never begin work without wiping off the table and instruments.
- Never work on a table cluttered with unneeded instruments or equipment’s.
- Never fold a drawing or a tracing.
- Sheet Layout
The paper is usually cut somewhat in larger dimension than the desired size of the drawing and trimmed to size after the work is finished. Suppose the finished size is to be 11 by 17 in. with a 1/2 in. border inside. Lay the scale down on the paper close to the lower edge and measure 17 in., marking the distance with the pencil; at the same time mark 1/2 in. inside at each end for the border line. Use a short dash forming a continuation of the division line on the scale in laying off a dimension. Do not bore a hole with the pencil. Near the left edge mark 11- and 1/2 -in. borderline points. Through these four marks on the left edge, draw horizontal lines with the T square; and through the points on the lower edge, draw vertical lines, using the triangle against the T square.
- Lettering
Graphic representation of the shape of a part, machine, or structure gives one aspect of the information needed for its construction. To this must be added, to complete the description, figured dimensions, notes on material and finish, and a descriptive title—all lettered, freehand, in a style that is perfectly legible, uniform, and capable of rapid execution. As far as the appearance of a drawing is concerned, the lettering is the most important part. But the usefulness of a drawing, too, can be ruined by lettering done ignorantly or carelessly, because illegible figures are apt to cause mistakes in the work.
By far the greatest amount of lettering on drawings is done in a rapid single-stroke letter, either vertical or inclined, and every engineer must have absolute command of these styles.
The term "single-stroke," or "one-stroke," does not mean that the entire letter is made without lifting the pencil or pen but that the width of the stroke of the pencil or pen is the width of the stem of the letter.
Single Stroke lettering
By far the greatest amount of lettering on drawings is done in a rapid single-stroke letter, either vertical or inclined, and every engineer must have absolute command of these styles.
The term "single-stroke," or "one-stroke," does not mean that the entire letter is made without lifting the pencil or pen but that the width of the stroke of the pencil or pen is the width of the stem of the letter.
|
Guidelines
Always draw light guide lines for both tops and bottoms of letters, using a sharp pencil. Figure 1 shows a method of laying off several equally spaced lines. Draw the first base line; then set the bow spacers to the distance wanted between base lines and step off the required number of base lines. Above the last line mark the desired height of the letters.
Lettering in Pencil
Good technique is as essential in lettering as in drawing. The quality of the lettering is important whether it appears on finished work to be reproduced by one of the printing processes or as part of a pencil drawing to be inked. In the first case, the penciling must be clean, firm, and opaque; in the second, it may be lighter.
Single - stroke Vertical Capitals:
The vertical, single-stroke, commercial Gothic letter is a standard for titles, reference letters, etc. As for the proportion of width to height, the general rule is that the smaller the letters are, the more extended they should be in width.
A low extended letter is more legible than a high compressed one and at the same time makes a better appearance.
Vertical lower-case letters:
The single-stroke, vertical lower-case letter is not commonly used on machine drawings but is used extensively in map drawing. It is the standard letter for hypsography in government topographic drawing. The bodies are made two-thirds the height of the capitals with the ascenders extending to the capital line and the descenders dropping the same distance below.
Single strokes Inclined capitals:
Many draftsmen use the inclined, or slant, letter in preference to the upright. The order and direction of strokes are the same as in the vertical form.
Single stroke, Inclined lower-case letters:
The inclined lower-case letters have bodies two-thirds the height of the capitals with the ascenders extending to the capital line and the descenders dropping the same distance below the base line. The lower-case letter is suitable for notes and statements on drawings because it is much more easily read than all capitals.
The loop letters are made with an ellipse whose long axis is inclined about 45° in combination with a straight line.
Plain scales: A plain scale consists of a line divided into suitable number of equal parts or units, the first of which is sub-divided into smaller parts. Plain scales represent either two units or a unit and its sub-division.
In every scale,
(i) The zero should be placed at the end of the first main division, i.e. between the unit and its sub-divisions.
(ii) From the zero mark, the units should be numbered to the right and its sub-divisions to the left.
(iii) The names of the units and the sub-divisions should be stated clearly below or at the respective ends.
(iv) The name of the scale (e.g. scale, 1: 10) or its R.F. should be mentioned below the scale.
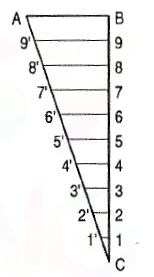Diagonal scales: A diagonal scale is used when very minute distances such as 0.1 mm etc. are to be accurately measured or when measurements are required in three units; for example, dm, cm and mm, or yard, foot and inch.
Small divisions of short lines are obtained by the principle of diagonal division, as explained below.
Principle of diagonal scale:
To obtain divisions of a given short line AB in multiples of 1/10 ~ its length, e.g. 0.1 AB, 0.2 AB, 0.3 AB etc. (fig.)
(i) At one end, say B, draw a line perpendicular to AB and along it, step-off ten equal divisions of any length, starting from B and ending at C.
(ii) Number the division-points, 9, 8, 7, ..... 1 as shown.
(iii) Join A with C.
(iv) Through the points 1, 2 etc. draw lines parallel to AB and cutting AC at 1 ', 2’ etc. It is evident that triangles 1 '1 C, 2'2C ... ABC are similar.
Since C5 = 0.5BC, the line 5'5 = 0.5AB.
Similarly, 1 '1 = 0.1AB, 2'2 = 0.2AB etc.
Thus, each horizontal line below AB becomes progressively shorter in length by -1 AB giving lengths in multiples of 0.1AB.
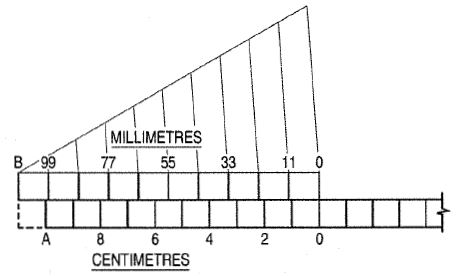
Vernier scales: Vernier scales, like diagonal scales, are used to read to a small unit with great accuracy. A Vernier scale consists of two parts - a primary scale and a Vernier. The primary scale is a plain scale fully divided into minor divisions.
As it would be difficult to sub-divide the minor divisions in the ordinary way, it is done with the help of the Vernier. The graduations on the Vernier are derived from those on the primary scale.
(a) Principle of Vernier: Fig. shows a part of a plain scale in which the length AO represents 10 cm. If we divide AO into ten equal parts, each part will represent 1 cm. It would not be easy to divide each of these parts into ten equal divisions to get measurements in millimetres.
|
Now, if we take a length BO equal to 10 + 1 = 11 such equal parts, thus representing 11 cm, and divide it into ten equal divisions, each of these divisions will represent 10/11 = 1.1 cm or 11mm.
The difference between one part of A0 and one division of B0 will be equal 1.1 – 1.0 = 0.1 cm or 1mm.
Similarly, the difference between two parts of each will be 0.2 cm or 2 mm.
The upper scale B0 is the Vernier. The combination of the plain scale and the Vernier is the Vernier scale.
(b) least count of a vernier: It is the difference of 1 primary scale division and 1 vernier scale division. It is denoted by angle C.
Angle C = 1 primary scale division - 1 vernier scale division.
The vernier scales are classified as under:
(i) Forward vernier: In this case, the length of one division of the vernier scale is smaller than the length of one division of the primary scale. The vernier divisions are marked in the same direction as that of the main scale.
(ii) Backward vernier: The length of each division of vernier scale is greater than the length of each division of the primary scale. The numbering is done in the opposite direction as that of the primary scale.
Use of elliptical curves is made in arches, bridges, dams, monuments, manholes,
glands and stuffing-boxes etc. Mathematically an ellipse can be described by
equation x2/ a2 + y2/b2 = 1. Here 'a' and 'b' are half the length of major and minor
axes of the ellipse and x and y co-ordinates.
(1) General method of construction of an ellipse:
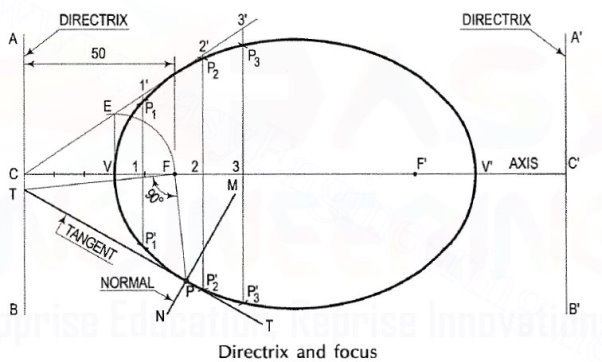
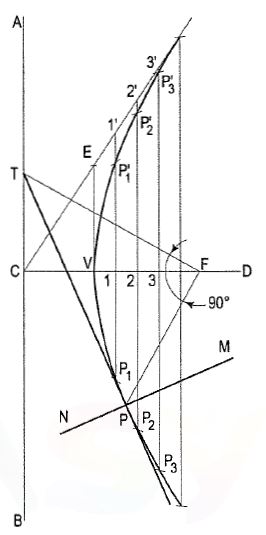
To construct an ellipse when the distance of the focus from the directrix is equal to 50 mm and eccentricity is 2/3.
(i) Draw any vertical line AB as directrix.
(ii) At any point C on it, draw the axis perpendicular to the AB (directrix).
(iii) Mark a focus F on the axis such that CF = 50 mm.
(iv) Divide CF into 5 equal divisions (sum of numerator and denometer of the
eccentricity.).
(v) Mark the vertex V on the third division-point from C.
Thus, eccentricity, e VF/VC = 2/3
(vi) A scale may now be constructed on the axis (as explained below), which
will directly give the distances in the required ratio.
(vii) At V, draw a perpendicular VE equal to VF. Draw a line joining C and E.
Thus, in triangle CVE, VE/VC = VF/VC = 2/3
(viii) Mark any point 1 on the axis and through it, draw a perpendicular
to meet CE-produced at 1 '.
(ix) With centre F and radius equal to 1-1 ', draw arcs to intersect the perpendicular through 1 at points P1 and P' 1.
These are the points on the ellipse, because the distance of P1 from AB
is equal to C1,
P1 F = 1-1'
1-1'/C1 = VF/VC = 2/3
Similarly, mark points 2, 3 etc. on the axis and obtain points P2 and P'2 , P3 and P'3 etc.
(x) Draw the ellipse through these points. It is a closed curve having two foci
and two directrices.
|
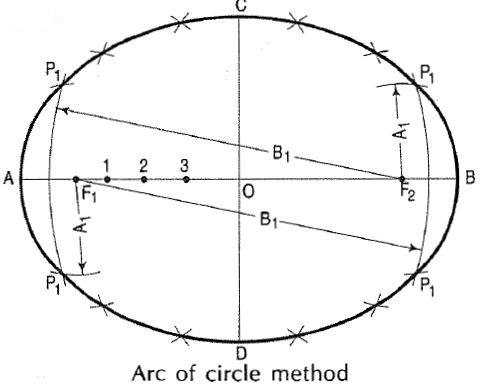
Arc of circle method:
(i) Draw a line AB equal to the major axis and a line CO equal to the minor axis, bisecting each other at right angles at 0.
(ii) With centre C and radius equal to half AB (i.e. AO) draw arcs cutting AB at F1 and F2, the foci of the ellipse.
(iii) Mark several points 1, 2, 3 etc. on AB.
(iv) With centres F1 and F2 and radius equal to A1, draw arcs on both sides of AB.
(v) With same centres and radius equal to B1, draw arcs intersecting the
previous arcs at four points marked P1.
(vi) Similarly, with radii A2 and B2, A3 and B3 etc. obtain more points.
(vii) Draw a smooth curve through these points. This curve is the required ellipse.
|
Use of parabolic curves is made in arches, bridges, sound reflectors, light
reflectors etc. Mathematically a parabola can be described by an equation y2 =4 ax or x2 = 4a y.
(1) General method of construction of a parabola:
Problem (fig.): To construct a parabola when the distance of the Focus from the directrix is 50 mm.
(i) Draw the directrix AB and the axis CD.
(ii) Mark focus F on CD, 50 mm from C.
(iii) Bisect CF in V the vertex (because eccentricity = 1).
(iv) Mark several points 1, 2, 3 etc. on the axis and through them, draw perpendiculars to it.
(v) With centre F and radius equal to C1, draw arcs cutting the perpendicular through 1 at P1 and P'1 .
(vi) Similarly, locate points P2 and P'2 , P3 and P'3 etc. on both the sides of the axis.
(vii) Draw a smooth curve through these points. This curve is the required parabola. It is an open curve.
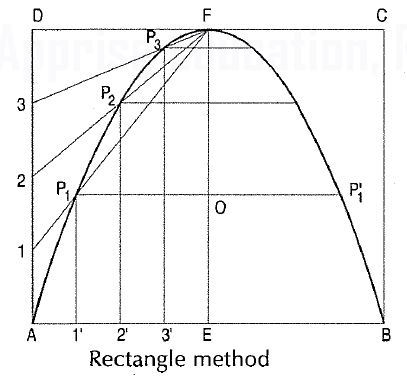
Rectangle method (fig.)
Problem . To construct a parabola given the base and the axis.
(i) Draw the base AB.
(ii) At its mid-point E, draw the axis ff at right angles to AB.
(iii) Construct a rectangle ABCD, making side BC equal to ff.
(iv) Divide AE and AD into the same number of equal parts and name them as shown (starting from A).
(v) Draw lines joining F with points 1, 2 and 3. Through 1 ', 2' and 3', draw perpendiculars to AB intersecting F1, F2 and F3 at points P1, P2 and P3 respectively.
(vi) Draw a curve through A, P1, P2 etc. It will be a half parabola. Repeat the same construction in the other half of the rectangle to complete the parabola. Or, locate the points by drawing lines through the points P1, P2 etc. parallel to the base and making each of them of equal length c on both the sides of ff, e.g. P10 = OP'1 . AB and EF are called the base and the axis respectively of the parabola.
|
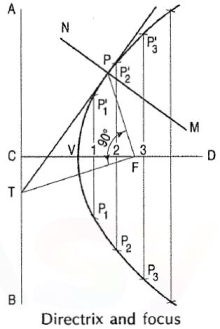
Construct a hyperbola, from the directrix is 65 mm and eccentricity is f
(i) Draw the directrix AB and the axis CD. when the distance of the focus
(ii) Mark the focus F on CD and 65 mm from C.
(iii) Divide CF into 5 equal divisions and mark V the vertex, on the second division from C.
Thus, eccentricity = VF/VC = 3/2
To construct the scale for the ratio ~ draw a line VE perpendicular to CD such that VE = VF. Join C with E.
Thus, in triangle CVE, VE/VC = VF/VC =3/2
(iv) Mark any point 1 on the axis and through it, draw a perpendicular to meet CE-produced at 1 '.
(v) With centre F and radius equal to 1-1 ', draw arcs intersecting the perpendicular through 1 at P1 and P'1·
(vi) Similarly, mark a number of points 2, 3 etc. and obtain points P2 and P'2 , P3 and P'3 etc.
(vii) Draw the hyperbola through these points.
Cycloid:
Cycloid is a curve generated by a point on the circumference of a circle which
rolls along a straight line. It can be described by an equation,
y = a (1 - cosθ) or x = a (θ - sinθ).
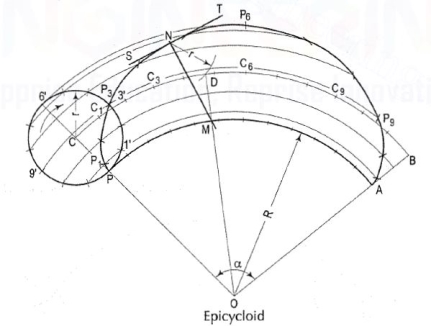
Epicycloid:
The curve generated by a point on the circumference of a circle, which rolls without slipping along another circle outside it, is called an epicycloid. The epicycloid can be represented mathematically by
|
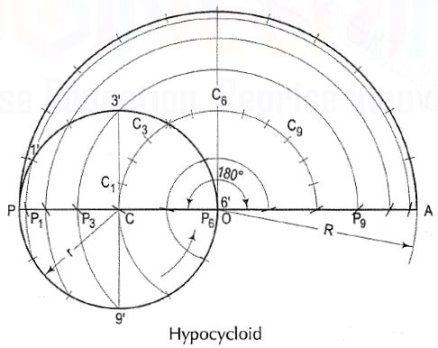
Hypocycloid (fig.): The method for drawing the hypocycloid is same as for epicycloid. Note that the centre C of the generating circle is inside the directing circle.
|
- Involute
The involute is a curve traced out by an end of a piece of thread unwound froma circle or a polygon, the thread being kept tight. It may also be defined as acurve traced out by a point in astraight line which rolls without slipping along acircle or a polygon.
It is used as teeth profile of gear wheel.
Mathematically it can be described as by , , where “r” is the radius of the circle.
