Unit 4
Fourier series and Vector Calculus
Full range Fourier series
Definition:
Fourier Series
Let f(x) be a periodic function of period 2L. Defined in the internal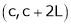 
and satisfied Dirichlet's conditions, then f(x) can be expressed as,
.
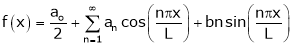Where ao, an, bn are called Fourier constant’s or Fourier coefficients and are given by,
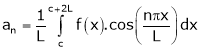
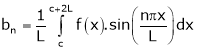
Note:
That there are only 4 intervals as below. i.e.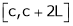 
is divided into following four intervals.
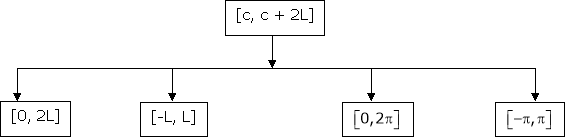
Note that for [0, 2L] we put c = 0
Hence Fourier series in this interval will be,
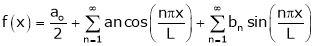
Where
Simillarly, for the interval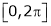 
we put c = 0,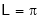 
Hence Fourier series in this interval will be
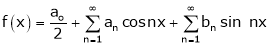
Where
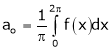
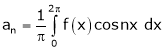
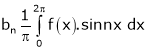
Note that for the interval [-L, L] i.e. put C = -L,
First we check whether f(x) is even function or odd.
Case I:-
If f(x) is even function. Then we get half range cosine series as,
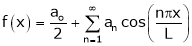
Where
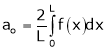
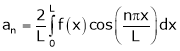
Case II:-
If f(x) is odd function. Then we get half range sine series as,
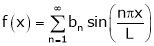
Where
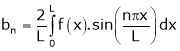
Simillarly
Note that for that interval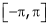 
i.e. put 
, 
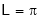
First we check wheatear f(x) is even or odd function.
Case I:-
If f(x) is even function then we get half range cosine series as
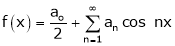
Where
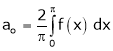
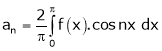
Case II:-
If f(x) is odd function then we get half range sine series as,
Where
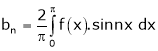
Note that
- For half range cosine series i.e. f(x) is even function bn = 0
- For half range sine series i.e. f(x) is odd function ao = an = 0
Exercise
Find the Fourier series of f(x) = x in the interval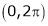 
Solution:
Here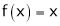 
; 
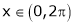
It’s Fourier series is given by
… (1)
Where
&
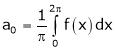
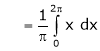
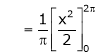
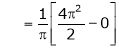
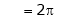
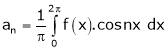
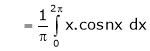
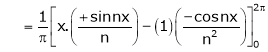
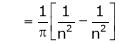
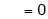
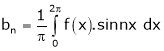
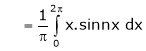
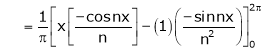
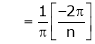
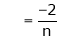
Hence the required Fourier series is
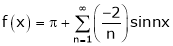
- Find the Fourier series for
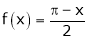in the interval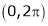 
Hence deduce that
Solution:
Here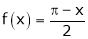 
; 
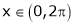
Hence it’s Fourier series is,
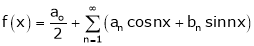… (1)
Where
&
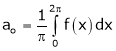
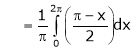
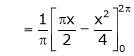
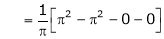
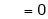
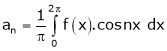
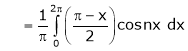
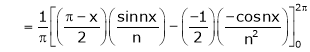
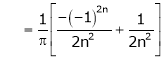
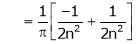
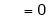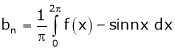
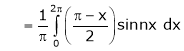
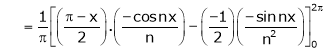
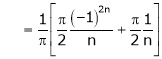
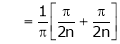
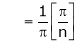
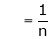
Hence equation (1) becomes
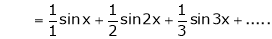
Put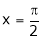 
we get
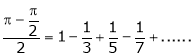
i.e.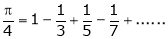 
2. Find a Fourier series expansion in the interval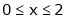 
for
; 
; 
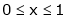
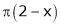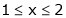
Solution:
Here
; 
; 
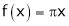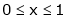
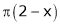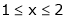
Hence it’s Fourier series expansion is,
… (1)
Where
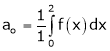
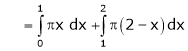
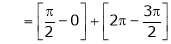
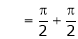
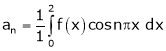
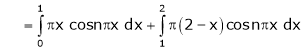
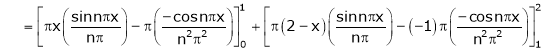
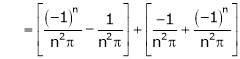
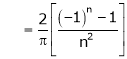
And
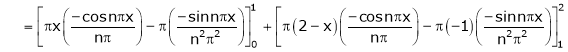
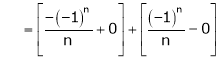
Hence equation (1) becomes
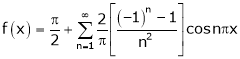
3. Find a Fourier series of
; 
; 
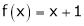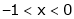
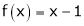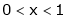
Solution:
Here
; 
; 
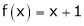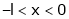
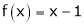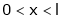
Here f(x) is odd function Hence we get half range sine series i.e.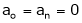 
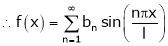… (1)
Where
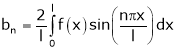
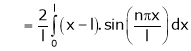
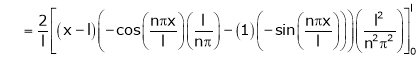
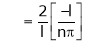
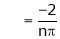
Hence equation (1) becomes,
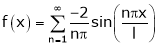
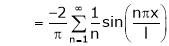
Half range Fourier series
4. Find a Fourier series for
; 
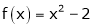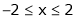
Solution:
Here
; 
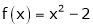Since f(x) is even function hence 
It’s Fourier series is
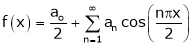… (1)
Where
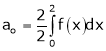
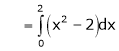
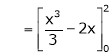
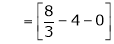
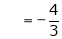
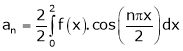
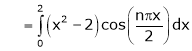
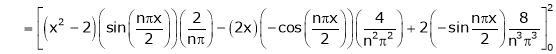
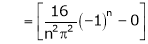
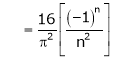
Hence equation (1) becomes,
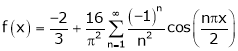
5. Find half range cosine series of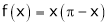 
in the interval 
and hence deduce that
a)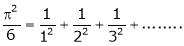 
b)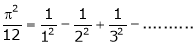 
Solution:
Here
; 
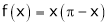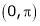
Hence it’s half range cosine series is,
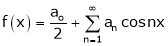… (1)
Where
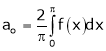
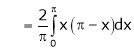
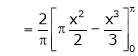
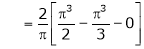
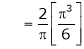
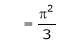
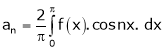
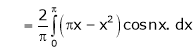
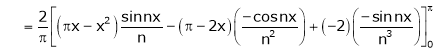
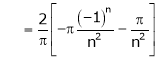
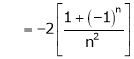
Hence equation (1) becomes,
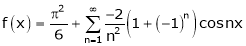
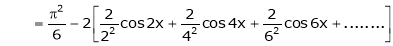
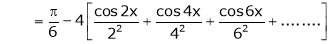… (2)
Put x = 0, we get
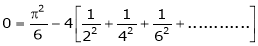
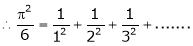
Hence the result
Put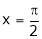 
we get,
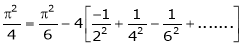
i.e. 
Cosine Series:
Example 1:
Using complex form,find the Fourier series of the function
f(x) = sinnx = 
Solution:
We calculate the coefficients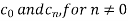 
= 
=
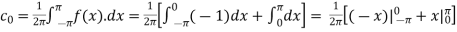
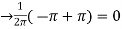
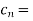
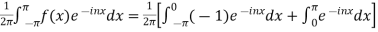
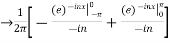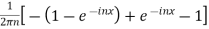
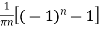
Hence the Fourier series of the function in complex form is
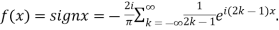
We can transform the series and write it in the real form by renaming as
n=2k-1,n=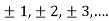
= 
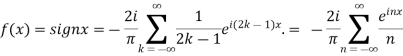
Example 2:
Using complex form find the Fourier series of the function f(x) = x2, defined on te interval [-1,1]
Solution:
Here the half-period is L=1.Therefore,the co-efficient c0 is,
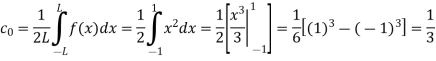
For n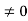
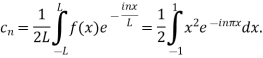
Integrating by parts twice,we obtain
= 
= 
= 
.
= 
.
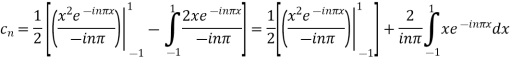
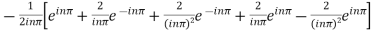
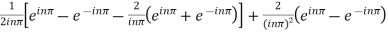
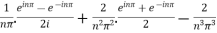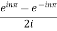
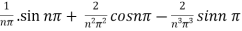Example 1: Find the gradient of the following:
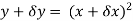
Solution: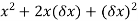 
y=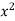
= 
.
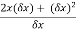= 2x+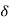
Example 2:
Find the curl of F(x,y,z) = 3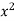
i+2zj-xk
Curl F =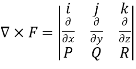 
=
= 
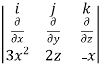
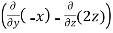i -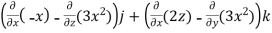 
= (0-2)i-(-1-0)j+(0-0)k
= -2i+j
Example 3:
What is the curl of the vector field F= ( x +y +z ,x-y-z,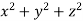
)?
Solution:
Curl F = 
= 
=
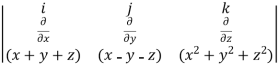
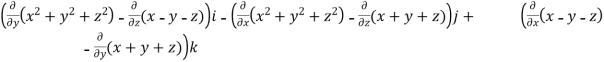
= (2y+1)i-(2x-1)j+(1-1)k
= (2y+1)i+(1-2x)j+0k
= (2y+1, 1-2x,0)
Example 4: Compute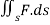 
where F= (3x+
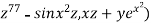and s is the surface of the box such that 0
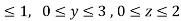use outward normal n
Solution: Writing the given vector fields in a suitable manner for finding divergence
Div F =3+2y+x
We use the divergence theorem to convert the surface integral into a triple integral
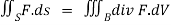
Where B is the box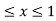 0
, 0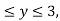
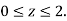
We compute the triple integral of div F=3+2y+x over the box B
=
=
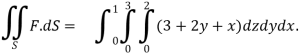
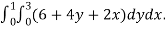
= 36+3=39
Example 5: For F= (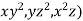
use divergence theorem to evaluate 
where s is the dphere of radius 3 centred at origin.
Solution: Since div F= 
, the surface integral is equal to the triple integral.
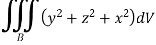
To evaluate the triple integral we can change value of variables to spherical co-ordinates,
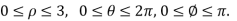
The integral is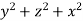 
=
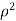.For spherical co-ordinates, we know that the jacobian determinant is dV = 
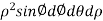.therefore, the integral is
= 
= 
=
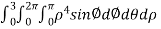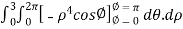
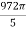
Reference Book:
1. G.B. Thomas and R.L. Finney, Calculus and Analytic geometry, 9th Edition, Pearson, Reprint, 2002.
2. Erwin kreyszig, Advanced Engineering Mathematics, 9th Edition, John Wiley & Sons,2006.
3. Veerarajan T., Engineering Mathematics for the first year, Tata McGraw-Hill, New Delhi,2008.
4. Ramana B.V., Higher Engineering Mathematics, Tata McGraw Hill New Delhi, 11th Reprint, 2010.
5. D. Poole, Linear Algebra: A Modern Introduction, 2nd Edition, Brooks/Cole, 2005.
6. B.S. Grewal, Higher Engineering Mathematics, Khanna Publishers, 36th Edition, 2010
