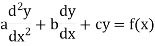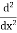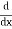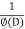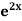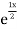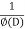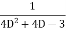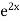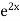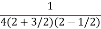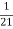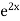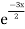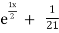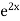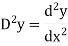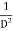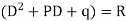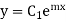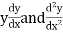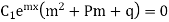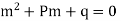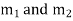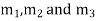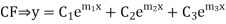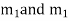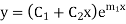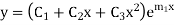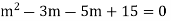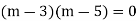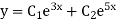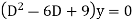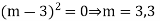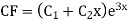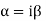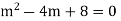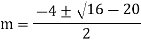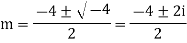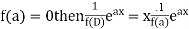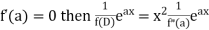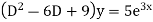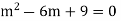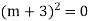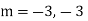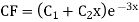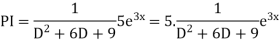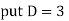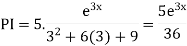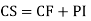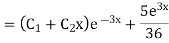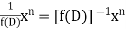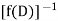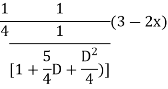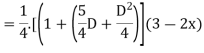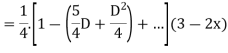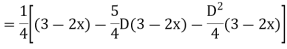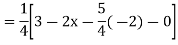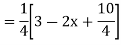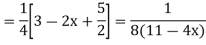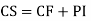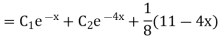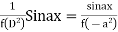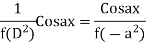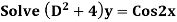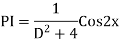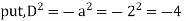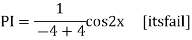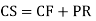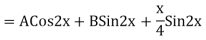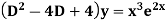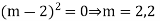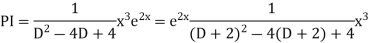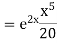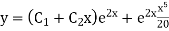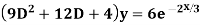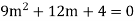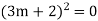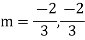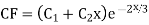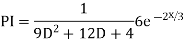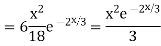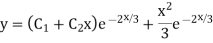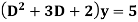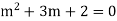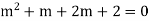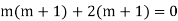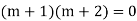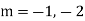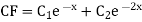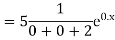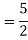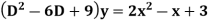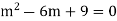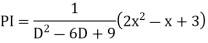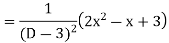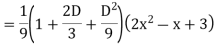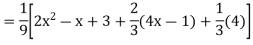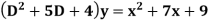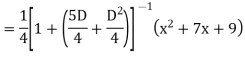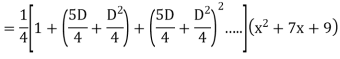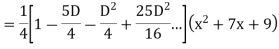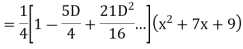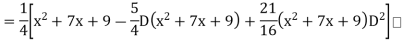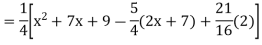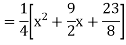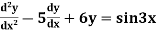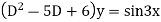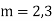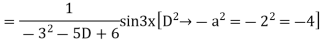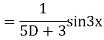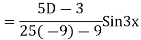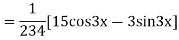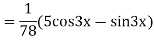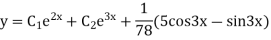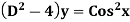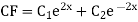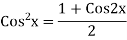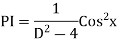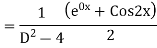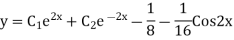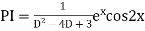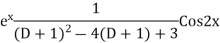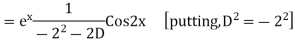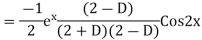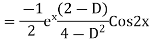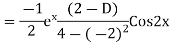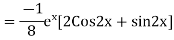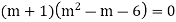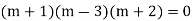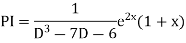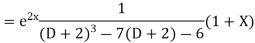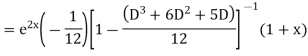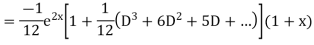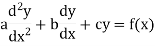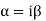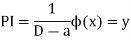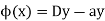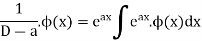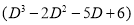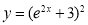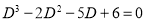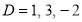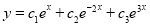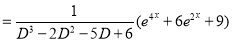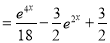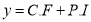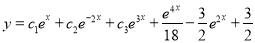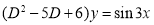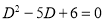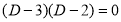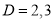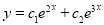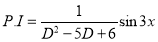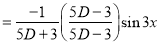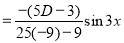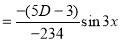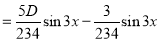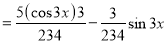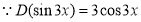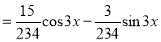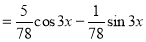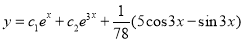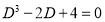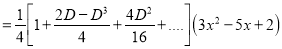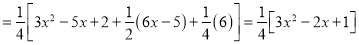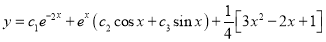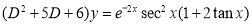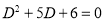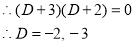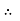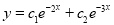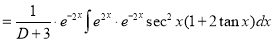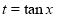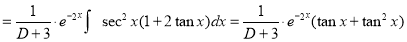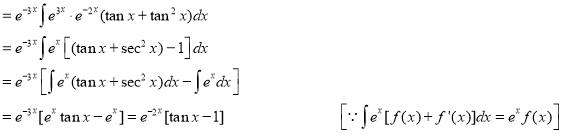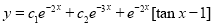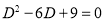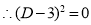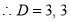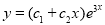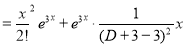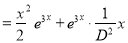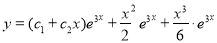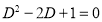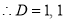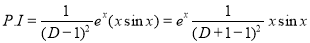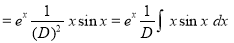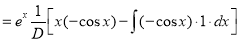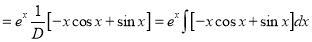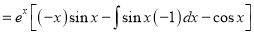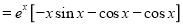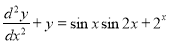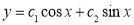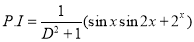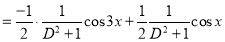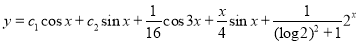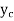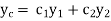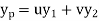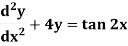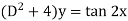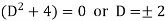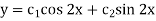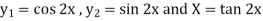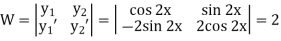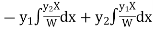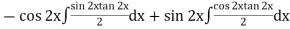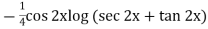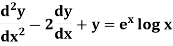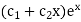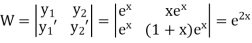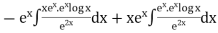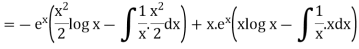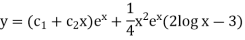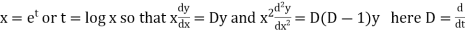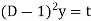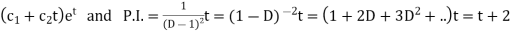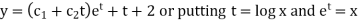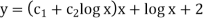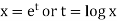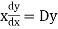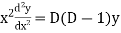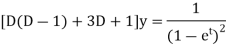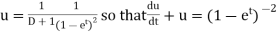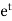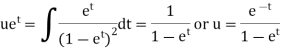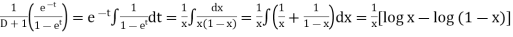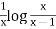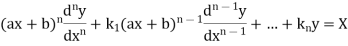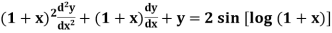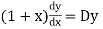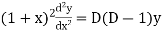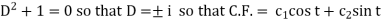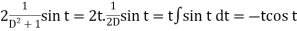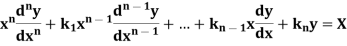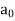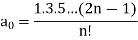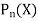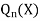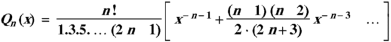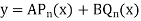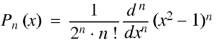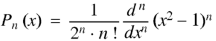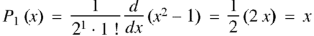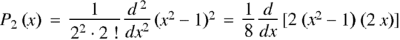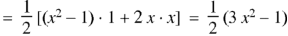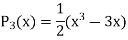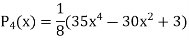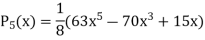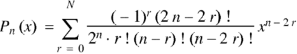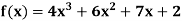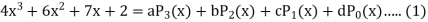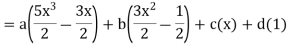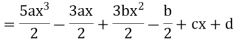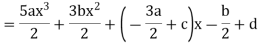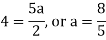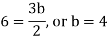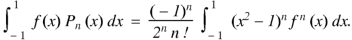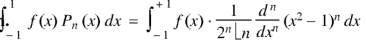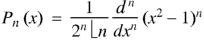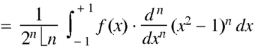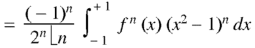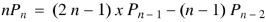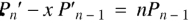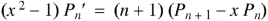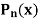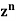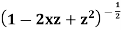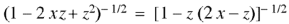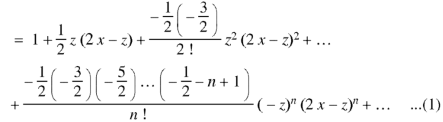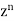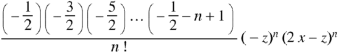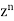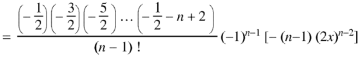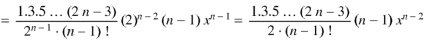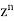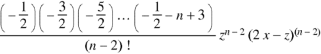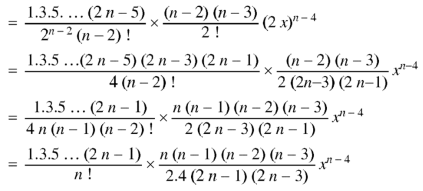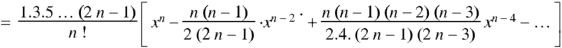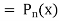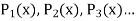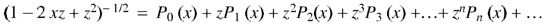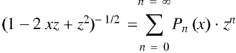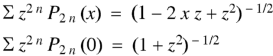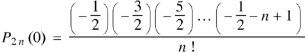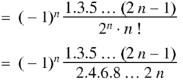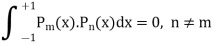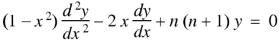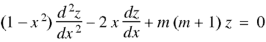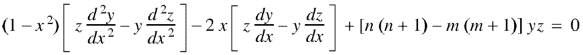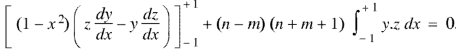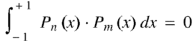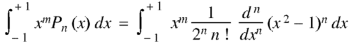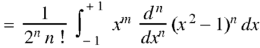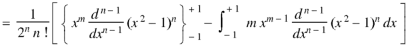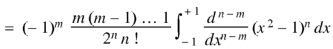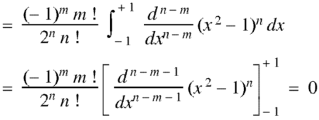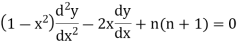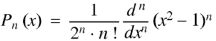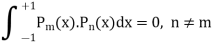UNIT-2
Linear differential equations
A homogeneous linear ordinary differential equation with constant coefficients is an ordinary differential equation in which coefficients are constants, all terms are linear, and the entire differential equation is equal to zero,
The form of second order linear differential equation with constant coefficients is,
Where a,b,c are the constants. Let, aD²y+bDy+cy = f(x), where d² = ∅(D)y = f(x) , where ∅(D)y = aD²y+bDy+cy |
Here first we solve, ∅(D)y = 0, which is called complementary function(C.F)
Then we find particular integral (P.I)
P.I. = General solution = C.F. +P.I. |
Let’s do an examples to understand the concept,
Example1: Solve (4D² +4D -3)y = |
Solution: Auxiliary equation is 4m² +4m – 3 = 0 We get, (2m+3)(2m – 1) = 0 m = complementary function: CF is A now we will find particular integral, P.I. = = = = = General solution is y = CF + PI = A |
Differential operators
D stands for operation of differential i.e.
Thus,
Note:-Complete solution = complementary function + Particular integral i.e. y=CF + PI |
Method for finding the CF
Step1:- In finding the CF right hand side of the given equation is replaced by zero.
Step 2:-
Let
Putting the value of
|
It is called auxiliary equation.
Step 3:- Roots Real and Different
If If |
Step 4- Roots Real and Equal
If both the roots are
If roots are
|
Example: Solve |
Ans. Given, Here Auxiliary equation is
|
Example: Solve |
Or,
Ans. Auxiliary equation are
Note: If roots are in complex form i.e.
|
Example : Solve |
Ans. Auxiliary equation are
|
Rules to find Particular Integral
Case 1: If, If, |
Example:Solve | |
Ans. Given, Auxiliary equation is
| |
Case2: Expand
| |
Case 3: Or,
| |
Case 4: Example: Solve Ans. AE=
Complete solution is | |
Example: Solve
Ans. The AE is
Complete solution y= CF + PI
| |
Example: Solve Ans. The AE is
Complete solution = CF + PI
| |
Example: Solve Ans. The AE is
Complete solutio0n is y= CF + PI
| |
Example: Find the PI of Ans.
| |
Example: solve Ans. Given equation in symbolic form is
Its Auxiliary equation is
Complete solution is y= CF + PI
| |
Example: Solve Ans. The AE is
We know,
Complete solution is y= CF + PI
| |
Example: Find the PI of(D2-4D+3)y=ex cos2x
Ans.
| |
Example. Solve(D3-7D-6) y=e2x (1+x)
Ans. The auxiliary equation i9s
Hence complete solution is y= CF + PI
|
Key takeaways-
Where a,b,c are the constants. 2. General solution = C.F. +P.I. 3. 4. 5. Roots Real and Equal-
6. Roots Real and Different-
7. If roots are in complex form i.e.
|
A general method of finding the PI of any function 
Or
Or
|
It is the LDE.
The solution will be-
|
Example: Solve |
Auxiliary equation
Complementary function
Complete Solution is
|
Example: Solve Solution: Auxiliary equation
C.F is
|
Example Solve Solution: The Auxiliary equation is
P.I
|
Example Solve Solution: The auxiliary equation is
|
Example Solve Solution: The auxiliary equation is
But
|
Example Solve Solution: The auxiliary equation is
|
Example Solve Solution: The auxiliary equation is
Now,
And
|
Method of variation of parameters-
Consider a second order LDE with constant co-efficient given by
Then let the complimentary function
Then the particular integral is
Where u and v are unknown and to be calculated using the formula u= |
Example-1: Solve the following DE by using variation of parameters-
|
Sol. We can write the given equation in symbolic form as-
To find CF- It’s A.E. is So that CF is- To find PI- Here Now Thus PI = = = = = So that the complete solution is-
|
Example-2: Solve the following by using the method of variation of parameters.
|
Sol. This can be written as-
C.F.- Auxiliary equation is- So that the C.F. will be- P.I.- Here Now Thus PI = = =
So that the complete solution is-
|
An equation of the form
|
Here X is the function of x, is called Cauchy’s homogeneous linear equation.
Example-1: Solve |
Sol. As it is a Cauchy’s homogeneous linear equation. Put Then the equation becomes [D(D-1)-D+1]y = t or Auxiliary equation-
So that- C.F.= Hence the solution is-
|
Example-2: Solve |
Sol. On putting
The given equation becomes-
Or it can be written as-
So that the auxiliary equation is- C.F. = Particular integral- Where It’s a Leibnitz’s linear equation having I.F.= Its solution will be-
P.I. = = So that the complete solution is-
An equation of the form-
Is called Legendre’s linear equation. |
Example-3: Solve |
Sol. As we see that this is a Legendre’s linear equation. Now put So that- And Then the equation becomes- D (D – 1)y+ Dy + y = 2 sin t
Its auxiliary equation is- And particular integral- P.I. = Note - Hence the solution is - |
Key takeaways-
Cauchy’s homogeneous linear equation-
|
The Legendre’s equations is-
|
Now the solution of the given equation is the series of descending powers of x is-
Here If n is a positive integer and
The above solution is So that-
Here Note- Legendre’s equations of second kind is
|
The general solution of Legendre’s equation is-
|
Here A and B are arbitrary constants.
Rodrigue’s formula-
Rodrigue’s formula can be defined as-
|
If n = 0, then it becomes-
If n = 1,
If n = 2,
Now putting n =3, 4, 5……..n we get-
…………………………………..
Where N = n/2 if n is even and N = 1/2 (n-1) if n is odd. |
Legendre Polynomials-
We know that by Rodrigue formula-
Example: Express |
Sol.
By equating the coefficients of like powers of x, we get-
Put these values in equation (1), we get-
|
Example: Let 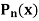 be the Legendre’s polynomial of degree n, then show that for every function f(x) for which the n’th derivative is continuous-
be the Legendre’s polynomial of degree n, then show that for every function f(x) for which the n’th derivative is continuous-
|
We know that-
On integrating by parts, we get-
Now integrate (n – 2) times by parts, we get-
|
Recurrence formulae for 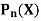 -
-
Formula-1:
Fromula-2:
Formula-3:
Formula-4:
Formula-5:
Formula-6:
|
Generating function for 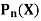 -
-
Prove that |
Proof:
Now coefficient of
Coefficient of
Coefficient of
And so on. Coefficient of
The coefficients of Therefore-
|
Example: Show that-
Sol. We know that
Equating the coefficients of
|
Orthogonality of Legendre polynomials-
Proof:
And
Now multiply (1) by z and (2) by y and subtracting, we have-
Now integrate from -1 to +1, we get-
|
Example: Prove that-
|
By using Rodrigue formula for Legendre function.
On integrating by parts, we get-
Now integrating m – 2 times, we get-
|
Key takeaways-
3. Orthogonality of Legendre polynomials-
|
References
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
- Higher engineering mathematics, HK Dass
- BV ramana, higher engineering mathematics