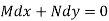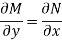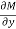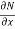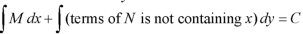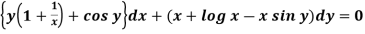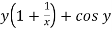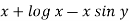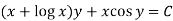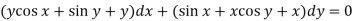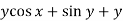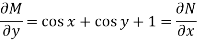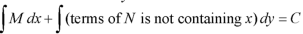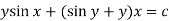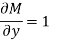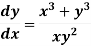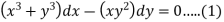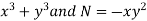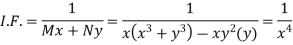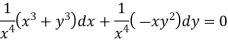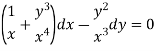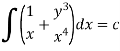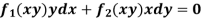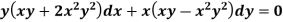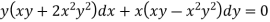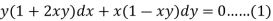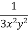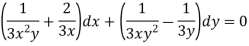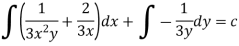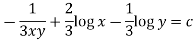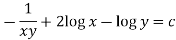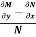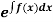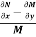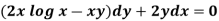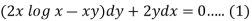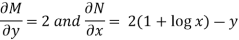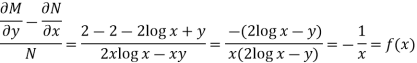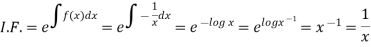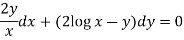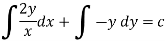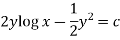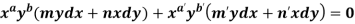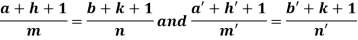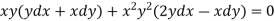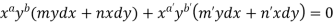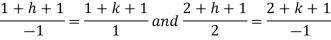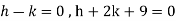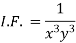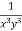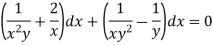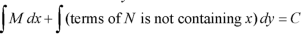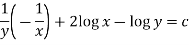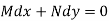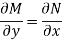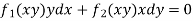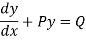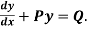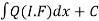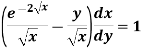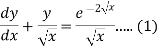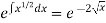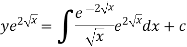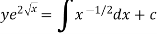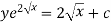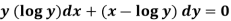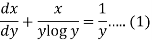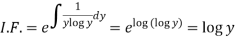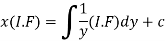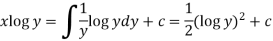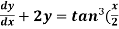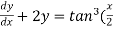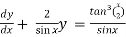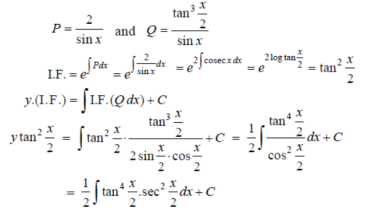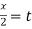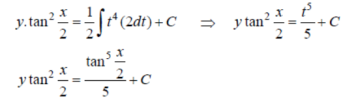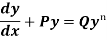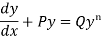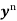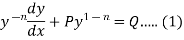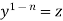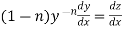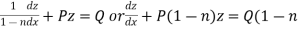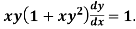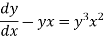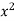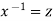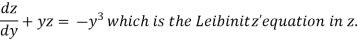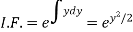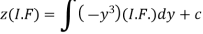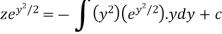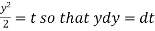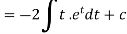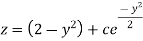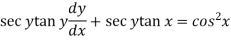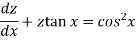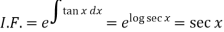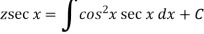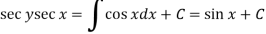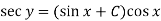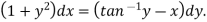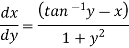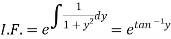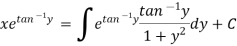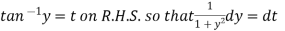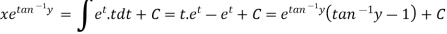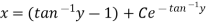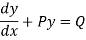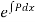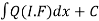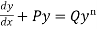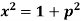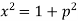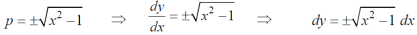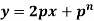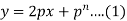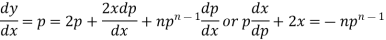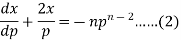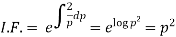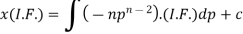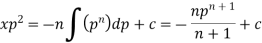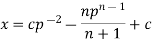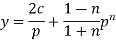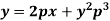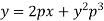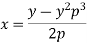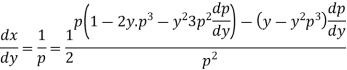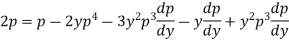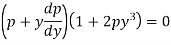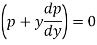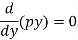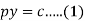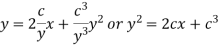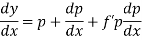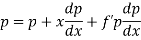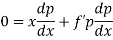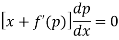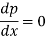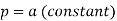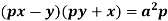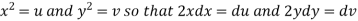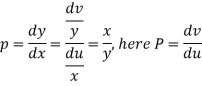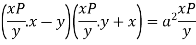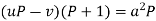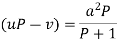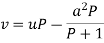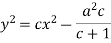Definition-
An exact differential equation is formed by differentiating its solution directly without any other process,
Is called an exact differential equation if it satisfies the following condition-
Here |
Step by step method to solve an exact differential equation-
1. Integrate M w.r.t. x keeping y constant.
2. Integrate with respect to y, those terms of N which do not contain x.
3. Add the above two results as below-
|
Example-1: Solve |
Sol. Here M =
Then the equation is exact and its solution is-
|
Example-2: Solve-
|
Sol. We can write the equation as below-
Here M = So that-
The equation is exact and its solution will be-
Or
|
Example-3: Determine whether the differential function ydx –xdy = 0 is exact or not.
Solution
. Here the equation is the form of M(x , y)dx + N(x , y)dy = 0 But, we will check for exactness,
|
 These are not equal results, so we can say that the given diff. eq. is not exact.
These are not equal results, so we can say that the given diff. eq. is not exact.
Equation reducible to exact form-
1. If M dx + N dy = 0 be a homogenous equation in x and y, then 1/ (Mx + Ny) is an integrating factor. |
Example: Solve-
Sol. We can write the given equation as-
Here, M =
Multiply equation (1) by
This is an exact differential equation-
|
2. I.F. for an equation of the type IF the equation Mdx + Ndy = 0 be this form, then 1/ (Mx – Ny) is an integrating factor. |
Example: Solve-
Sol. Here we have- Now divide by xy, we get-
Multiply (1) by
Which is an exact differential equation-
|
3. In the equation M dx + N dy = 0, (i) If (ii) If |
Example: Solve-
Sol. Here given,
M = 2y and N = 2x log x - xy Then-
Here,
Then,
Now multiplying equation (1) by 1/x, we get-
|
4. For the following type of equation-
An I.F. is Where-
|
Example: Solve-
Sol. We can write the equation as below-
Now comparing with-
We get- a = b = 1, m = n = 1, a’ = b’ = 2, m’ = 2, n’ = -1 I.F. = Where-
On solving we get- h = k = -3
Multiply the equation by
It is an exact equation. So that the solution is-
|
Key takeaways-
Is called an exact differential equation if it satisfies the following condition-
2. If M dx + N dy = 0 be a homogenous equation in x and y, then 1/ (Mx + Ny) is an integrating factor. 3. I.F. for an equation of the type IF the equation Mdx + Ndy = 0 be this form, then 1/(Mx – Ny) is an integrating factor. |
A differential equation of the form
|
Is called linear differential equation.
It is also called Leibnitz’s linear equation.
Here P and Q are the function of x
Working rule
(1)Convert the equation to the standard form (2) Find the integrating factor. (3) Then the solution will be y (I.F) = |
Note- 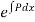 is called the integrating factor.
is called the integrating factor.
Example-1: Solve-
|
Sol. We can write the given equation as-
So that- I.F. = The solution of equation (1) will be-
Or
Or
Or
|
Example-2: Solve-
|
Sol. We can write the equation as-
We see that it is a Leibnitz’s equation in x- So that-
Therefore the solution of equation (1) will be-
Or
|
Example-3: Solve sin x |
Solution: here we have, sin x
Now,
Put tan
Which is the required solution. |
Bernoulli’s equation-
The equation
|
Is reducible to the Leibnitz’s linear equation and is usually called Bernoulli’s equation.
Working procedure to solve the Bernoulli’s linear equation-
Divide both sides of the equation - By
Put Then equation (1) becomes-
|
Here we see that it is a Leibnitz’s linear equations which can be solved easily.
Example: Solve |
Sol. We can write the equation as-
On dividing by
Put Equation (1) becomes,
Here,
Therefore the solution is-
Or
Now put
Integrate by parts-
Or |
Example: Solve |
Sol. here given,
Now let z = sec y, so that dz/dx = sec y tan y dy/dx Then the equation becomes-
Here,
Then the solution will be-
|
Example: Solve- |
Sol. here given-
We can re-write this as-
Which is a linear differential equation-
The solution will be-
Put
|
Key takeaways-
Is called linear differential equation 2. 3. y (I.F) = 4. The equation |
Example- Solve-
|
Sol. Here we have-
or
On integrating, we get- |
Equation solvable for y-
Steps-
First- differentiate the given equation w.r.t. x.
Second- Eliminate p from the given equation, then the eliminant is the required solution.
Example: Solve |
Sol. Here we have-
Now differentiate it with respect to x, we get-
Or
This is the Leibnitz’s linear equation in x and p, here
Then the solution of (2) is-
Or
Or
Put this value of x in (1), we get
|
Equation solvable for x-
Example: Solve-
|
Sol. Here we have-
On solving for x, it becomes-
Differentiating w.r.t. y, we get-
or
On solving it becomes
Which gives-
Or
On integrating
Thus eliminating from the given equation and (1), we get
Which is the required solution |
.Clairaut’s equation-
An equation
y = px + f(p) ...... (2) |
is known as Clairaut’s equation.
Differentiating (1) w.r.t. x, we get-
Put the value of p in (1) we get- y = ax + f(a) Which is the required solution. |
Example: Solve-
|
Sol. Put So that-
Then the given equation becomes-
Or
Or
Which is the Clairaut’s form. Its solution is-
i.e.
|
Key takeaways-
|
References
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
- Higher engineering mathematics, HK Dass
- BV ramana, higher engineering mathematics