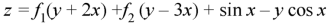Module 3
Partial differential equations
A differential equation involving partial derivatives with respect to more than one independent variable is called a partial differential equation.
The independent variables will be denoted by x and y and the dependent variable by z. The partial differential coefficients are denoted as-
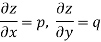
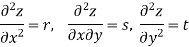
ORDER of a partial differential equation is the same as that of the order of the highest differential coefficient in it.
Classification of partial differential equation-
Suppose the equation is-
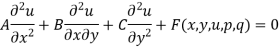
Here A, B, C are the constants of x and y, then the equation-
1. Elliptical- if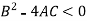 
2. Parabolic- if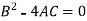 
3. Hyperbolic- if if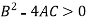 
Formation of partial differential equation-
Method of elimination of arbitrary constants-
Example: Form a partial differential equation from-
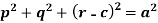
Sol.
Here we have-
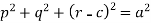
It contains two arbitrary constants a and c
Differentiate the equation with respect to p, we get-
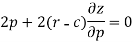
Or
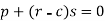
Now differentiate the equation with respect to q, we get-
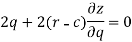
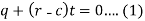
Now eliminate ‘c’,
We get
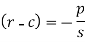
Now put z-c in (1), we get-
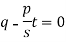
Or
The second method we use is method of elimination of arbitrary function.
Solution of partial differential equation by direct partial Integration-
Example: Solve-
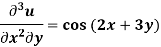
Sol.
Here we have-
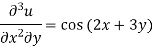
Integrate w.r.t. x, we get-
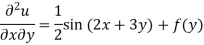
Integrate w.r.t. x, we get-
Integrate w.r.t. y, we get-
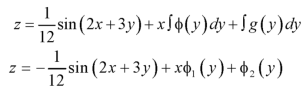
Example: Solve the differential equation-
Given the boundary condition that-
At x = 0,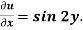 
Sol.
Here we have-
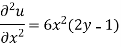
On integrating partially with respect to x, we get-
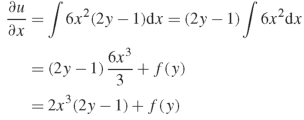
Here f(y) is an arbitrary constant.
Now form the boundary condition-
When x = 0,
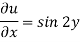
Hence-
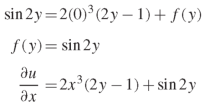
On integrating partially w.r.t.x, we get-
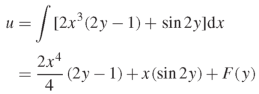
Example: Solve the differential equation-
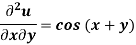
Given that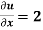 
when y = 0, and u = 
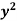when x = 0.
Sol.
We have-
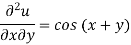
Integrating partially w.r.t. y, we get-
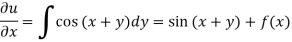
Now from the boundary conditions,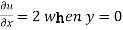 
Then-
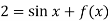
From which,
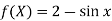
It means,
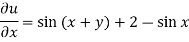
On integrating partially w.r.t. x givens-
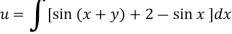
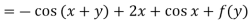
From the boundary conditions, u =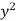 
when x = 0
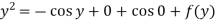
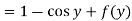
From which-
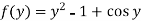
Therefore the solution of the given equation is-
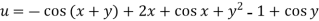
Lagrange’s linear equation in an equation of the type-
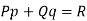
Here P, Q and R are the functions of x, y, z and p =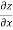 
and q =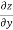 
Working steps to solve-
Step-1: Write down the auxiliary equation-
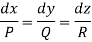
Step-2: Solve the auxiliary equations-
Suppose the two solutions are- u =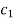 
and v =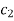 
Step-3: Then f(u, v) = 0 or u = ∅(v) is the required solution of
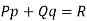
Method of multipliers-
Let the auxiliary equation be
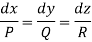
L, m, n may be the constants of x, y, z then we have-
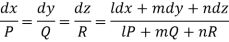
L, m, n are selected in a such a way that-
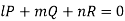
Thus
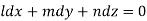
On solving this differential equation, if the solution is- u =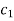 
Similarly, choose another set of multipliers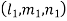 
and if the second solution is v =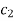 
So that the required solution is f(u, v) = 0.
Example: Solve-
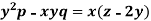
Sol.
We have-
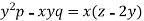
Then the auxiliary equations are-
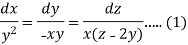
Consider first two equations only-
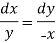
On integrating
…….. (2)
Now consider last two equations-
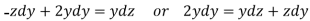
On integrating we get-
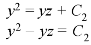…………… (3)
From equation (2) and (3)-
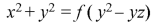
Example: Find the general solution of-
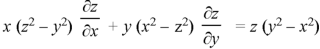
Sol. The auxiliary simultaneous equations are-
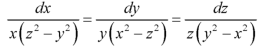……….. (1)
Using multipliers x, y, z we get-
Each term of (1) is equals to-
Xdx + ydy + zdz=0
On integrating-
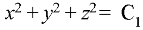………… (2)
Again equation (1) can be written as-
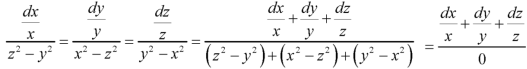
Or
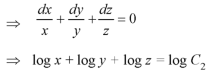
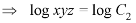
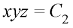………….. (3)
From (2) and (3), the general solution is-
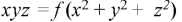
Non-linear partial differential equations-
Type-1: Equation of the type f(p, q) = 0
Method-
Let the required solution is-
Z = ax + by + c …….. (1)
So that-
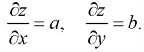
On putting these values in f(p, q) = 0
We get-
f(a, b) = 0
So from this, find the value of b in terms of a and put the value of b in (1). It will be the required solution.
Type-2: Equation of the type-
Z = px + qy + f(p, q)
Its solution will be-
Z = ax + by + f(a, b)
Type-3: Equation of the type f(z, p, q) = 0
Type-4: Equation of the type-
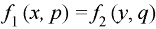
Method-
Let-
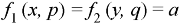
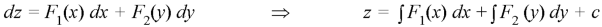
Example: Solve-
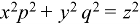
Sol.
This equation can be transformed as-
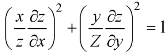
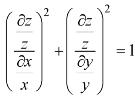………. (1)
Let
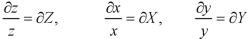
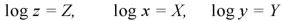
Equation (1) can be written as-
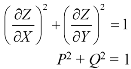………… (2)
Let the required solution be-
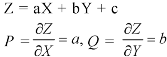
From (2) we have-
Example: Solve-
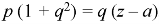
Sol.
Let u = x + by
So that-
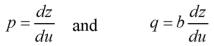
Put these values of p and q in the given equation, we get-
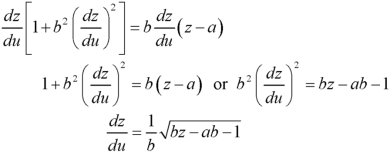
Example: Solve-
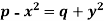
Sol.
Let-
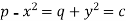
That means-
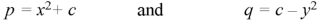
Put these values of p and q in
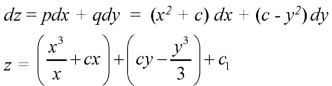
An equation of the type-
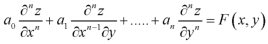
Is called a homogeneous linear partial differential equation of n’th order with constant coefficient.
Rules for finding the complementary functions
Let us consider the equation-
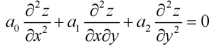
Or
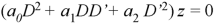
Step-1: Put D = m and D’ = 1
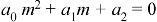
This is the auxiliary equation.
Step-2: Solve the auxiliary equation.
Case-1: If roots of the auxiliary equation are real and different, say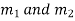 
Then C.F.-
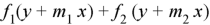
Case-2: If roots are equal-
Then C.F.
Rules for finding P.I.-
Given partial differential equation is-
f(D, D’)z = F(x, y)
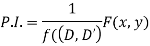
1. When F(x, y) =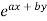 
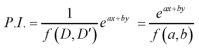
Put D = a and D’ = b
2. When F(x, y) = sin (ax + by) or cos(ax+ by)
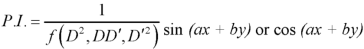
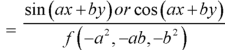
Put 
3. When F(x, y) =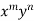 
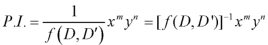
Expand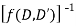 
is ascending power of D and D’ and operate on 
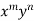term by term.
4. When F(x,y) any function.
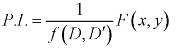
Resolve 1/f(D,D’) into partial fractions.
Considering f(D, D’) as a function of D alone
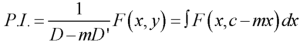
Here c is replaced by y + mx after integration.
Example: Solve-
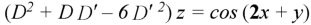
Sol.
Here we have-
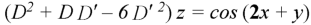
Auxiliary equation will be-
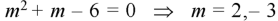
C.F.-
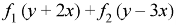
P.I.-
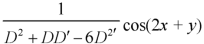
Here
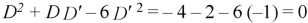
This is the case of failure.
Now-
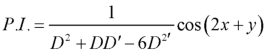
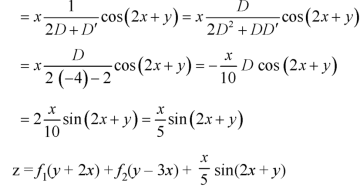
Example: Solve-
Sol.
The given equations can be written in the form of-
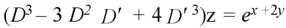
Its auxiliary equation is-
We get-
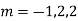
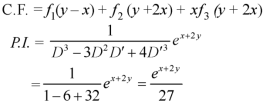
Put D = 1, D’ = 2, -
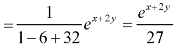
Therefore the complete solution is-
Example: Solve-
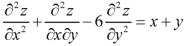
Sol.
This equation can be written as-
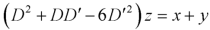
Writing D = m and D’ = 1, then the auxiliary equation will be-
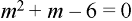
m = -3, 2
C.F.-
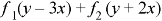
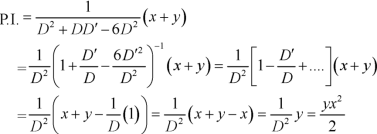
Hence the complete solution is-
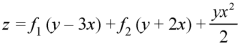
Example: Solve-
Sol.
The given partial differential equation can be written in the form-
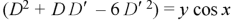
A.E.-
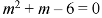
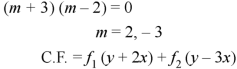
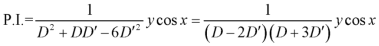
Put y = c + 3x
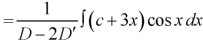
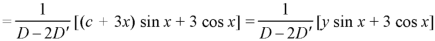
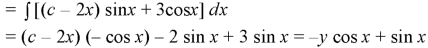
Hence the complete solution is-
