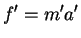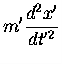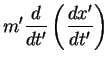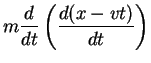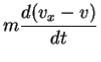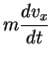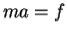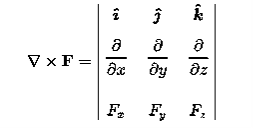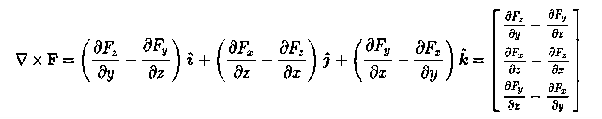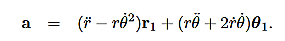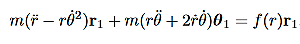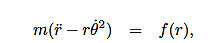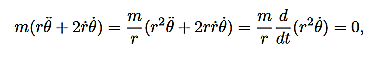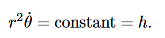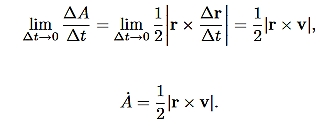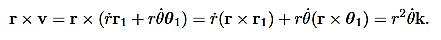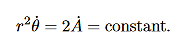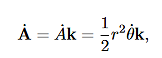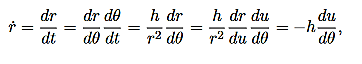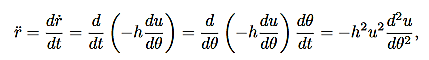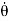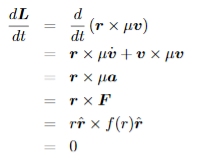UNIT-III
VECTOR MECHANICS
Certain physical quantities such as mass or the absolute temperature at some point in space only have magnitude. A single number can represent each of these quantities, with appropriate units, which are called scalar quantities. There are, however, other physical quantities that have both magnitude and direction. Force is an example of a quantity that has both direction and magnitude (strength). Three numbers are needed to represent the magnitude and direction of a vector quantity in a three dimensional space. These quantities are called vector quantities.
Vector quantities also satisfy two distinct operations, vector addition and multiplication of a vector by a scalar. We can add two forces together and the sum of the forces must satisfy the rule for vector addition. We can multiply a force by a scalar thus increasing or decreasing its strength. Position, displacement, velocity, acceleration, force, and momentum are all physical quantities that can be represented mathematically by vectors. The set of vectors and the two operations form what is called a vector space. There are many types of vector spaces but we shall restrict our attention to the very familiar type of vector space in three dimensions that most students have encountered in their mathematical courses.
Vectors are sets of three quantities that transform in the same manner as the coordinates of a point P.
- Having a magnitude and direction is not sufficient to define a vector.
- Some transformations cannot be written in terms of a series of rotations. An example is an inversion. These are called improper rotations.
- Transformations that can be written in terms of a series of rotations are called proper rotations.
The laws of Physics are invariant'' under rotations of the coordinate system.
Rotational symmetry of laws of Physics implies conservation of Angular Momentum.
We will work with Passive Rotations'' where we rotate the coordinate axes rather than active rotations'' where we rotate the physical system and keep the axes fixed. These are essentially the same thing except the rotation angle changes sign.
A vector is a mathematical object that transforms in a particular way under rotations.
We know there are also physical quantities called scalars that are invariant under rotations.
Very often in practical problems, the components of a vector are known in one coordinate system but it is necessary to find them in some other coordinate system.
The relationship between the components in one coordinate system and the components in a second coordinate system are called the transformation equations. Any change of Cartesian coordinate system will be due to a translation of the base vectors and a rotation of the base vectors. A translation of the base vectors does not change the components of a vector.
Rotation of object relative to FIXED axis:
Basic equations you can get by looking at the diagram above:
x1= rcosα …………(1)
x2=rcos(θ+α) …………(2)
y1=rsinα …………(3)
y2=rsin(θ+α) …………(4)
|
Figure 1: Rotation of object relative to fixed axis
Using trigonometric results the equations (2) and (4) become
x2=rcos(θ+α)
=rcosθcosα–rsinθsinα
=(rcosα)cosθ–(rsinα)sinθ
=x1cosθ–y1sinθ …………(5)
y2=rsin(θ+α)
=rsinθcosα+rcosθsinα
=(rcosα)cosθ+(rsinα)cosθ
=x1sinθ+y1cosθ …………(6)
Hence, For an anti-clockwise rotation,
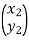 =
= 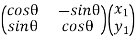 …………(7)
…………(7)
is called the rotation matrix. Its determinant is 1.
To find the clockwise rotation matrix, you can do the calculations again. OR you can just transpose the above matrix OR you can substitute −θ into the matrix.
Hence, the clockwise rotation matrix is: 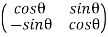
Note: Since clockwise rotation means rotating in the anti-clockwise direction by −θ, you can just substitute −θ into the anti-clockwise matrix to get the clockwise matrix. Since cos is an even function, it will not be affected by the −θ. (- cos x = cos x)
Rotation of coordinate axes:
|
Figure 2: Rotation of coordinate axes
Basic equations:
x′=rcosα …………(8)
x=rcos(θ+α) …………(9)
y′=rsin …………(10)
y=rsin(θ+α) …………(11)
Using trigonometric results the equations (9) and (11) become
x=rcos(θ+α)
=rcosθcosα–rsinθsinα
=x′cosθ–y′sinθ …………(12)
y=rsin(θ+α)
=rsinθcosα+rcosθsinα
=x′sinθ+y′cosθ …………(13)
From equation (13) So we have
x′=  …………(14)
…………(14)
y′= 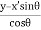 …………(15)
…………(15)
Substitute the above (14) and (15) equations into equation (12) and you will get:
y′=−xsinθ+ycosθ
x′=xcosθ+ysinθ
Hence,
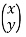 =
= 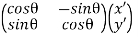 …………(16)
…………(16)
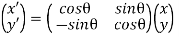 …………(17)
…………(17)
Key Takeaways
- Some transformations cannot be written in terms of a series of rotations. An example is an inversion. These are called improper rotations.
- Transformations that can be written in terms of a series of rotations are called proper rotations.
- The relationship between the components in one coordinate system and the components in a second coordinate system are called the transformation equations.
- Rotation of object relative to fixed axis is given as; For an anti-clockwise rotation,
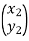 =
= 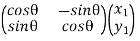 is called the rotation matrix. Its determinant is 1 and the clockwise rotation matrix is given as
is called the rotation matrix. Its determinant is 1 and the clockwise rotation matrix is given as 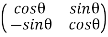
- Rotation of coordinate axes is given as
 =
= 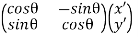 and
and 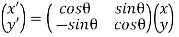
A fundamental force of nature is an attraction or repulsion between objects as described through interactions between fields and particles.
Physics has identified four basic types of these interactions, which together describe every action we see in the Universe, from the decay of atomic particles to the drift of entire galaxies.
From walking on the street, to launching a rocket into space, to sticking a magnet on your refrigerator, physical forces are acting all around us. But all the forces that we experience every day (and many that we don't realize we experience every day) can be whittled down to just four fundamental forces:
- Electromagnetic Force
- Gravitational Force
- Strong Nuclear Force
- Weak Nuclear Force
These are called the four fundamental forces of nature, and they govern everything that happens in the universe.
- Electromagnetic Force
This is the second strongest force after the strong force and it acts on electrically charged particles. It has strength of 1/137 relative to the strong force but has an infinite range. However, this force has both attractive and repulsive properties due to the two charges it possesses; negative and positive. Objects of like charge will have a repulsive effect on each other, while objects of unlike charges will have an attractive effect and this can be demonstrated with a simple magnet or electric charges.
This is the force that's most obvious in our day-to-day lives. Thanks to the interactions of negatively-charged electrons and positively-charged protons, it allows single atoms to combine into different materials. The force is also carried through the electromagnetic field by a particle called a photon, which thanks to chemical changes in our eyes our bodies sense as light.
For the sake of convenience, we distinguish the two different kinds of charges by associating an algebraic sign with q, and for this reason we talk about negative and positive charges. The electrostatic force Fb on charge qb due to charge qa is given by Coulomb's law: k is a constant of proportionality and rab is a unit vector which points from a to b. If qa and qb are both negative or both positive, the force is repulsive, but if the charges are of different sign, Fb is attractive.
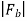 = -
= - 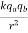
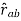
In the SI system, the unit of charge is the coulomb, abbreviated C. (The coulomb is defined in terms of electric currents and magnetic forces.) In this system, k is found by experiment to be
k = 8.99 x 109 N·m2/C2
2. Gravitational Force
This force is the weakest but has an infinite range. It has strength of 6 × 10-39 in comparison to the strength of the strong force. This force is always attractive acts between any two pieces of matter in nature. The effect of this gravitational force is dependent upon the mass of the two bodies and the distance between them.
Gravity is an attractive force between masses, which according to general relativity occurs as a result of the effect of energy acting on a space-time field. While theory suggests it could have a mediating particle - called a graviton - experiments are yet to support its existence.
While gravity might appear to be a strong force, responsible for holding entire galaxies together and squeezing the literal daylight out of stars, it's approximately 1029 times weaker than the weak nuclear force. That means it has virtually no observable effect on the scale of tiny particles, becoming relevant only on a more cosmic level.
Consider two particles, a and b, with masses Ma and Mb, respectively, separated by distance r. Let Fb be the force exerted on particle b by particle a.
|
Figure 3: Gravitational Force
Our verbal description of the magnitude of the force is summarized by
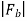 =
= 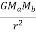
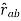
G is a constant of proportionality called the gravitational constant. Its value is found by measuring the force between masses in a known geometry. The first measurements were performed by Henry Cavendish in 1771 using a torsion balance.
The modern value of G is 6.67 X 10-11 N·m2/kg2. (G is the least accurately known of the fundamental constants. Perhaps you can devise a new way to measure it more precisely.) Experimentally, G is the same for all materials-aluminum, lead, neutrons, or what have you. For this reason, the law is called the universal law of gravitation.
3. Strong Nuclear Force
The strong nuclear force is what holds together the nuclei of atoms. This force holds the nucleus of an atom together. It is the strongest of the forces, but it is very short ranged. It acts over a range of about 10-15m, which is the average diameter of a medium sized nucleus. This force is attractive.
The protons and neutrons making up an atom's nucleus are themselves made up of a trio of simpler particles called quarks. A particle called a gluon acts on a property of quarks called colour, creating the force's pull.
Unlike the other three fundamental forces, the further the gluon needs to travel, the stronger the nuclear force gets. On the scale of protons and neutrons, this spring-like effect makes it incredibly hard to pull quarks apart. This helps explain why the strong force is so, well, strong.
On a scale of an atom's entire nucleus, the force also binds whole protons and neutrons to each other. Protons also push each other away thanks to the electromagnetic force, putting atomic nuclei into a delicate balance.
4. Weak Nuclear Force
This force is weak compared to the strong force as the name implies and has the shortest range of 10-18m, which is 0.1% of the diameter of a proton. It is responsible for radioactive decay especially nuclear beta decay. All particles experience this force.
Of all the fundamental forces, the weak nuclear force is the trickiest to grasp. It describes how the quarks that make up nuclear particles can change from one form into another. The force is carried by particles called W and Z bosons.
The weak force acts over an incredibly short distance, equal to about 0.1 percent of the diameter of a proton. When a particle such as a neutrino comes right up close to a quark, the weak force causes the quark to change by sending out a W boson. This can turn a neutron into a proton (creating a whole new element in the process), and the neutrino into an electron.
So We have studied that every pair of particles in the universe had its own special interaction, the task would be impossible. Fortunately, nature is kinder than this. As far as we know, there are only four fundamentally different types of interactions in the universe: gravity, electromagnetic interactions, the so-called weak interaction, and the strong interaction. Gravity and the electromagnetic interactions can act over a long range because they decrease only as the inverse square of the distance. However, the gravitational force always attracts, whereas electrical forces can either attract or repel. In large systems, electrical attraction and repulsion cancel to a high degree, and gravity alone is left. For this reason, gravitational forces dominate the cosmic scale of our universe. In contrast, the world immediately around us is dominated by the electrical forces, since they are far stronger than gravity on the atomic scale. Electrical forces are responsible for the structure of atoms, molecules, and more complex forms of matter, as well as the existence of light. The weak and strong interactions have such short ranges that they are important only at nuclear distances, typically 10-16 m.
They are negligible even at atomic distances, 10-10 m. As its name implies, the strong interaction is very strong, much stronger than the electromagnetic force at nuclear distances. It is the "glue" that binds the atomic nucleus, but aside from this it has little effect in the everyday world. The weak interaction plays a less dramatic role; it mediates in the creation and destruction of neutrinos-particles of no mass and no charge which are essential to our understanding of matter but which can be detected only by the most arduous experiments. Our object in the remainder of the chapter is to become familiar with the forces which are important in everyday mechanics. Two of these, the forces of gravity and electricity, are fundamental and cannot be explained in simpler terms. The other forces we shall discuss, friction, the contact force, and the viscous force, can be understood as the macroscopic manifestation of interatomic forces.
Key Takeaways
- A fundamental force of nature is an attraction or repulsion between objects as described through interactions between fields and particles.
- Physics has identified four basic types of these interactions, which together describe every action we see in the Universe, from the decay of atomic particles to the drift of entire galaxies.
- We experience four fundamental forces: Electromagnetic Force, Gravitational Force, Strong Nuclear Force and Weak Nuclear Force.
- These are called the four fundamental forces of nature, and they govern everything that happens in the universe.
The principles of dynamics were clearly stated for the first time by Sir Isaac Newton (1642–1727); today we call them Newton’s laws of motion. The first law states that when the net force on a body is zero, its motion doesn’t change. The second law tells us that a body accelerates when the net force is not zero. The third law relates the forces that two interacting bodies exert on each other. Newton did not derive the three laws of motion, but rather deduced them from a multitude of experiments performed by other scientists, especially Galileo Galilei (who died the year Newton was born). Newton’s laws are the foundation of classical mechanics (also called Newtonian mechanics); using them, we can understand most familiar kinds of motion. Newton’s laws need modification only for situations involving extremely high speeds (near the speed of light) or very small sizes (such as within the atom).
NEWTON’S FIRST LAW
How do the forces that act on a body affect its motion? To begin to answer this question, let’s first consider what happens when the net force on a body is zero. You would almost certainly agree that if a body is at rest, and if no net force acts on it (that is, no net push or pull), that body will remain at rest. But what if there is zero net force acting on a body in motion? To see what happens in this case, suppose you slide a hockey puck along a horizontal table top, applying a horizontal force to it with your hand (Figure 4).
Figure 4: Table: puck stops short After you stop pushing, the puck does not continue to move indefinitely; it slows down and stops. To keep it moving, you have to keep pushing (that is, applying a force). You might come to the “common sense” conclusion that bodies in motion naturally come to rest and that a force is required to sustain motion.
Figure 5: Table: Ice: puck slides farther But now imagine pushing the puck across a smooth surface of ice (Figure 5). After you quit pushing, the puck will slide a lot farther before it stops. Put it on an air-hockey table, where it floats on a thin cushion of air, and it moves still farther (Figure 6).
Figure 6: Air-hockey table: puck slides even farther
|
In each case, what slows the puck down is friction, an inter-action between the lower surface of the puck and the surface on which it slides. Each surface exerts a friction force on the puck that resists the puck’s motion; the difference in the three cases is the magnitude of the friction force. The ice exerts less friction than the table top, so the puck travels farther. The gas molecules of the air-hockey table exert the least friction of all.
If we could eliminate friction completely, the puck would never slow down, and we would need no force at all to keep the puck moving once it had been started. Thus the “common sense” idea that a force is required to sustain motion is incorrect. Experiments like the ones we’ve just described show that when no net force acts on a body, the body either remains at rest or moves with constant velocity in a straight line. Once a body has been set in motion, no net force is needed to keep it moving. We call this observation Newton’s first law of motion.
Newton’s First law can also be written as
A body acted on by no net force has a constant velocity (which may be zero) and zero acceleration
The tendency of a body to keep moving once it is set in motion is called inertia.
It’s important to note that the net force is what matters in Newton’s first law
Example
Suppose a hockey puck rests on a horizontal surface with negligible friction, such as an air-hockey table or a slab of wet ice.
|
Figure 7: (a) A hockey puck accelerates in the direction of a net applied force  . (b) When the net force is zero, the acceleration is zero, and the puck is in equilibrium.
. (b) When the net force is zero, the acceleration is zero, and the puck is in equilibrium.
If the puck is initially at rest and a single horizontal force 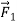 acts on it (Figure 7a), the puck starts to move. If the puck is in motion to begin with, the force changes its speed, its direction, or both, depending on the direction of the force. In this case the net force is equal to
acts on it (Figure 7a), the puck starts to move. If the puck is in motion to begin with, the force changes its speed, its direction, or both, depending on the direction of the force. In this case the net force is equal to 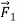 which is not zero. (There are also two vertical forces: the earth’s gravitational attraction and the upward normal force exerted by the surface. But as we mentioned earlier, these two forces cancel.)
which is not zero. (There are also two vertical forces: the earth’s gravitational attraction and the upward normal force exerted by the surface. But as we mentioned earlier, these two forces cancel.)
Now suppose we apply a second force, 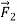 (Figure 7b), equal in magnitude to
(Figure 7b), equal in magnitude to 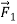 but opposite in direction. The two forces are negatives of each other,
but opposite in direction. The two forces are negatives of each other,
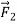
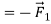 ,and their vector sum is zero
,and their vector sum is zero
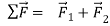
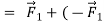
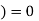
Again, we find that if the body is at rest at the start, it remains at rest; if it is initially moving, it continues to move in the same direction with constant speed. These results show that in Newton’s first law, zero net force is equivalent to no force at all. This is just the principle of superposition of forces.
When a body is either at rest or moving with constant velocity (in a straight line with constant speed), we say that the body is in equilibrium. For a body to be in equilibrium, it must be acted on by no forces, or by several forces such that their vector sum that is, the net force is zero.
NEWTON’S SECOND LAW
Newton’s first law tells us that when a body is acted on by zero net force, the body moves with constant velocity and zero acceleration. In Figure 8(a), a hockey puck is sliding to the right on wet ice. There is negligible friction, so there are no horizontal forces acting on the puck; the downward force of gravity and the upward normal force exerted by the ice surface sum to zero. So the net force 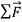 acting on the puck is zero, the puck has zero acceleration, and its velocity is constant.
acting on the puck is zero, the puck has zero acceleration, and its velocity is constant.
But what happens when the net force is not zero?
In Figure 8 (b) we apply a constant horizontal force to a sliding puck in the same direction that the puck is moving. Then 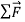 is constant and in the same horizontal direction as
is constant and in the same horizontal direction as  . We find that during the time the force is acting, the velocity of the puck changes at a constant rate; that is, the puck moves with constant acceleration. The speed of the puck increases, so the acceleration
. We find that during the time the force is acting, the velocity of the puck changes at a constant rate; that is, the puck moves with constant acceleration. The speed of the puck increases, so the acceleration  is in the same direction as
is in the same direction as 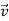 and
and  .
.
In Figure 8(c) we reverse the direction of the force on the puck so that  acts opposite to
acts opposite to 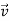 . In this case as well, the puck has acceleration; the puck moves more and more slowly to the right. The acceleration
. In this case as well, the puck has acceleration; the puck moves more and more slowly to the right. The acceleration 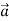 in this case is to the left, in the same direction as
in this case is to the left, in the same direction as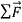 . As in the previous case, experiment shows that the acceleration is constant if
. As in the previous case, experiment shows that the acceleration is constant if 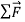 is constant. We conclude that net force acting on a body causes the body to accelerate in the same direction as the net force. If the magnitude of the net force is constant, as in Figures 8(b) and 8(c), then so is the magnitude of the acceleration.
is constant. We conclude that net force acting on a body causes the body to accelerate in the same direction as the net force. If the magnitude of the net force is constant, as in Figures 8(b) and 8(c), then so is the magnitude of the acceleration.
|
Figure 8: Using a hockey puck on a friction-less surface to explore the relationship between the net force  on a body and the resulting acceleration
on a body and the resulting acceleration 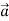 of the body.
of the body.
Our results mean that for a given body, the ratio of the magnitude 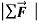 of the net force to the magnitude a=
of the net force to the magnitude a= 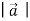 of the acceleration is constant, regardless of the magnitude of the net force. We call this ratio the inertial mass, or simply the mass, of the body and denote it by m. That is,
of the acceleration is constant, regardless of the magnitude of the net force. We call this ratio the inertial mass, or simply the mass, of the body and denote it by m. That is,
m= 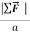 or
or 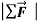 =ma or a=
=ma or a= 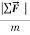
Mass is a quantitative measure of inertia. The above equations says that the greater a body’s mass, the more the body “resists” being accelerated. When you hold a piece of fruit in your hand at the supermarket and move it slightly up and down to estimate its heft, you’re applying a force and seeing how much the fruit accelerates up and down in response. If a force causes a large acceleration, the fruit has a small mass; if the same force causes only a small acceleration, the fruit has a large mass.
One newton is the amount of net force that gives an acceleration of 1 meter per second squared to a body with a mass of 1 kilogram.
For the same net force, the ratio of the masses of two bodies is the inverse of the ratio of their accelerations.
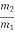 =
= 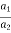 So Newton’s second law States that
So Newton’s second law States that
If a net external force acts on a body, the body accelerates. The direction of acceleration is the same as the direction of the net force. The mass of the body times the acceleration vector of the body equals the net force vector
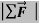 =ma
=ma
Newton’s second law is a fundamental law of nature, the basic relationship be-tween force and motion.
The statement of Newton’s second law refers to external forces. It’s impossible for a body to affect its own motion by exerting a force on itself; if it were possible, you could lift yourself to the ceiling by pulling up on your belt. That’s why only external forces are included in the sum 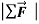 .
.
The design of high-performance motorcycles depends fundamentally on Newton’s second law. To maximize the forward acceleration, the designer makes the motorcycle as light as possible (that is, minimizes the mass) and uses the most powerful engine possible (thus maximizing the forward force).Light weight body (small m) Powerful engine (large F)application Blame Newton’s Second Law.
The above equations are valid only when the mass m is constant. It ’s easy to think of systems whose masses change, such as a leaking tank truck, a rocket ship, or a moving railroad car being loaded with coal. Such systems are better handled by using the concept of momentum.
Finally, Newton’s second law is valid in inertial frames of reference only, just like the first law. Thus it is not valid in the reference frame of any of the accelerating vehicles relative to any of these frames; the passenger accelerates even though the net force on the passenger is zero. We will usually assume that the earth is an adequate approximation to an inertial frame, although because of its rotation and orbital motion it is not precisely inertial.
Here is something important to discuss that m is not a force even though the vector m
is not a force even though the vector m is equal to the vector sum
is equal to the vector sum 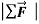 of all the forces acting on the body, the vector m
of all the forces acting on the body, the vector m is not a force. Acceleration is a result of a nonzero net force; it is not a force itself. It’s “common sense” to think that there is a “force of acceleration” that pushes you back into your seat when your car accelerates forward from rest. But there is no such force; instead, your inertia causes you to tend to stay at rest relative to the earth, and the car accelerates around you, The “common sense” confusion arises from trying to apply Newton’s second law where it isn’t valid—in the non-inertial reference frame of an accelerating car. We will always examine motion relative to inertial frames of reference only.
is not a force. Acceleration is a result of a nonzero net force; it is not a force itself. It’s “common sense” to think that there is a “force of acceleration” that pushes you back into your seat when your car accelerates forward from rest. But there is no such force; instead, your inertia causes you to tend to stay at rest relative to the earth, and the car accelerates around you, The “common sense” confusion arises from trying to apply Newton’s second law where it isn’t valid—in the non-inertial reference frame of an accelerating car. We will always examine motion relative to inertial frames of reference only.
NEWTON’S THIRD LAW
Force acting on a body is always the result of its interaction with another body, so forces always come in pairs. You can’t pull on a doorknob without the door-knob pulling back on you. When you kick a football, the forward force that your foot exerts on the ball launches it into its trajectory, but you also feel the force the ball exerts back on your foot. In each of these cases, the force that you exert on the other body is in the opposite direction to the force that body exerts on you. Experiments show that whenever two bodies interact, the two forces that they exert on each other are always equal in magnitude and opposite in direction. This fact is called Newton’s third law of motion:
If body A exerts a force on body B (an “action”), then body B exerts a force on body A (a “reaction”). These two forces have the same magnitude but are opposite in direction. These two forces act on different bodies.
Or
To every action there is equal and opposite reaction.
For example, 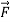 A on B is the force applied by body A (first sub-script) on body B (second subscript), and
A on B is the force applied by body A (first sub-script) on body B (second subscript), and  B on A is the force applied by body B(first subscript) on body A (second subscript).
B on A is the force applied by body B(first subscript) on body A (second subscript).
|
Figure 9: Newton’s third law of motion
In equation form,
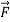 A on B =
A on B = 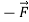 B on A
B on A
In the statement of Newton’s third law, “action” and “reaction” are the two opposite forces; we sometimes refer to them as an action–reaction pair. This is not meant to imply any cause-and-effect relation-ship; we can consider either force as the “action” and the other as the “reaction.” We often say simply that the forces are “equal and opposite,” meaning that they have equal magnitudes and opposite directions. the two forces in an action–reaction pair act on different bodies We stress that the two forces described in Newton’s third law act on different bodies.
The action and reaction forces are contact forces that are present only when the two bodies are touching. But Newton’s third law also applies to long-range forces that do not require physical contact, such as the force of gravitational attraction. A table-tennis ball exerts an upward gravitational force on the earth that’s equal in magnitude to the downward gravitational force the earth exerts on the ball. When you drop the ball, both the ball and the earth accelerate toward each other. The net force on each body has the same magnitude, but the earth’s acceleration is microscopically small because its mass is so great. Nevertheless, it does move.
Key Takeaways
- The principles of dynamics were clearly stated for the first time by Sir Isaac Newton (1642–1727); today we call them Newton’s laws of motion.
- The first law states that when no net force acts on a body, the body either remains at rest or moves with constant velocity in a straight line. Once a body has been set in motion, no net force is needed to keep it moving.
- The second law If a net external force acts on a body, the body accelerates. The direction of acceleration is the same as the direction of the net force. The mass of the body times the acceleration vector of the body equals the net force vector
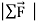 =ma
=ma - The third law states that; To every action there is equal and opposite reaction.
Suppose there are two reference frames (systems) designated by S and S' such that the coordinate axes are parallel. In S, we have the co-ordinates {x,y,z,t} and in S' we have the co-ordinates {x’,y’,z’,t’}. S' is moving with respect to S with velocity v (as measured in S) in the x direction. The clocks in both systems were synchronised at time t=0 and they run at the same rate.
Figure 10: Reference frame S' moves with velocity v (in the x direction) relative to reference frame S.
We have the intuitive relationships
x’ = x-vt
y’=y
z’=z
t’=t
This set of equations is known as the Galilean Transformation. They enable us to relate a measurement in one inertial reference frame to another. For example, suppose we measure the velocity of a vehicle moving in the in x-direction in system S, and we want to know what would be the velocity of the vehicle in S'.
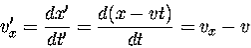 ………..(1)
………..(1)
This is the result our intuition is familiar with.
We have stated that we would like the laws of physics to be the same in all inertial reference frames, as this is indeed our experience of nature. Physically, we should be able to perform the same experiments in different reference frames, and find always the same physical laws. Mathematically, these laws are expressed by equations. So, we should be able to transform'' our equations from one inertial reference frame to the other inertial reference frame, and always find the same answer.
We will check that Newton's Second Law is the same in two different reference frames. We put one observer in the un-primed frame and the other in the primed frame, moving with velocity 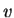 relative to the un-primed frame. Consider the vehicle of the previous case undergoing a constant acceleration in the x-direction,
relative to the un-primed frame. Consider the vehicle of the previous case undergoing a constant acceleration in the x-direction,
v is constant so we have
|
Indeed, it does not matter which inertial frame we observe from, we recover the same Second Law of Motion each time. We say the Second Law of Motion is invariant under the Galilean Transformation.
Key Takeaways
- x’ = x-vt, y’=y, z’=z and t’=t. This set of equations is known as the Galilean Transformation. They enable us to relate a measurement in one inertial reference frame to another.
- Second Law of Motion is invariant under the Galilean Transformation.
Potential energy is energy which results from position or configuration. The SI unit for energy is the joule = newton x meter in accordance with the basic definition of energy as the capacity for doing work.
An object may have the capacity for doing work as a result of its position in a gravitational field (gravitational potential energy), an electric field (electric potential energy), or a magnetic field (magnetic potential energy). It may have elastic potential energy as a result of a stretched spring or other elastic deformation.
If force acting on an object is a function of position only, it is said to be a conservative force, and it can be represented by a potential energy function which for a one-dimensional case satisfies the derivative condition
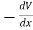 = F(x) ………….(1)
= F(x) ………….(1)
The integral form of this relationship is
V(x) = 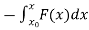 ………….(2)
………….(2)
which can be taken as a definition of potential energy
Note that there is an arbitrary constant of integration in that definition, showing that any constant can be added to the potential energy. Practically, this means that you can set the zero of potential energy at any point which is convenient.
The potential energy V is equal to the work you must do to move an object from the V=0 reference point to the position r. The reference point at which you assign the value V=0 is arbitrary, so may be chosen for convenience, like choosing the origin of a coordinate system.
The force on an object is the negative of the derivative of the potential function V. This means it is the negative of the slope of the potential energy curve. Plots of potential functions are valuable aids to visualizing the change of the force in a given region of space.
If the potential energy function V is known, the force at any point can be obtained by taking the derivative of the potential.
F in the definition of potential energy is the force exerted by the force field, e.g., gravity, spring force, etc. The potential energy V is equal to the work you must do against that force to move an object from the V=0 reference point to the position r. The force you must exert to move it must be equal but oppositely directed, and that is the source of the negative sign. The force exerted by the force field always tends toward lower energy and will act to reduce the potential energy.
The negative sign on the derivative shows that if the potential V increases with increasing r, the force will tend to move it toward smaller r to decrease the potential energy.
For Example
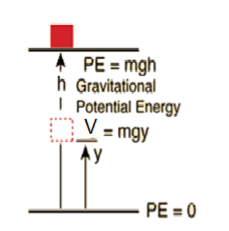
(i) Gravitational Potential energy V at a height h is given as mgh.
Fy = 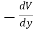
Fy = 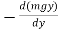
Fy = 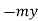
|
Figure 11: Potential energy
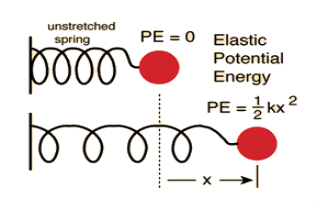
(ii) Spring-Mass System
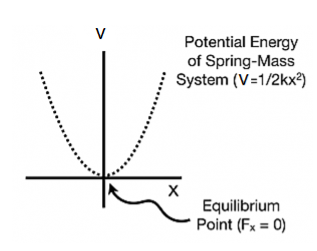
We know that Elastic potential energy of unstreched spring V is zero and Elastic potential energy of streched spring V is given by 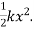 Here, the potential energy is quadratic (bowl-shaped) function. The force is zero at x=0. At that point, the slope of the potential energy graph is also zero. This point is stable because it is at the bottom of the “bowl-shaped” potential energy. Also, the force to the right side of the equilibrium point is pointing to the left (F=−kx<0 because x>0) and the force to the left side of the equilibrium point is pointing to the right (F=−kx>0 because x<0).
Here, the potential energy is quadratic (bowl-shaped) function. The force is zero at x=0. At that point, the slope of the potential energy graph is also zero. This point is stable because it is at the bottom of the “bowl-shaped” potential energy. Also, the force to the right side of the equilibrium point is pointing to the left (F=−kx<0 because x>0) and the force to the left side of the equilibrium point is pointing to the right (F=−kx>0 because x<0).
Fx = 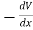
Fx = 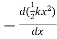
Fx = 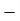 kx
kx
|
Figure 12: Spring-Mass System
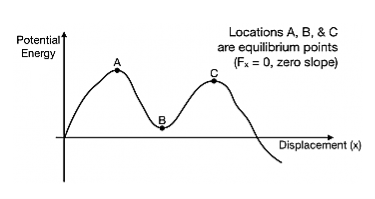
In a more general potential energy diagram (to the right), you can determine the equilibrium points by finding where the slope is zero (Fx=0). The stability of those points can be classified as stable or unstable.
|
Figure 13: Potential energy curve
A way to think about stability is to think of a bead sitting at the equilibrium location. Is it stable against small pushes? For example, at location B, a small push on the bead would cause the bead to move up a bit, but it would come back – location B is stable. At location A and C, a bead given a small push would run away from those locations – both are unstable.
|
Figure 14: Potential Energy-Displacement Curve
Similarly we can obtain potential energy if the value of force is known, by integrating force as given in equation (2).
To find the force in three-dimensions, this derivative of the potential becomes the gradient of the potential,
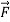 =−
=−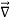 V=⟨
V=⟨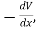
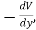
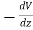 ⟩
⟩
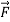 = =
= =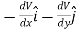

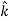
The triangle vector is called the gradient operator, or "del," and can be written like this:
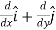
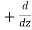

is called a vector operator, because it has components like a vector and its partial derivatives operate on a quantity placed to its right. When operating on a scalar function such as potential energy, it is also called the gradient operator. To simplify the notation, we write
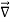 ≡
≡ 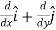
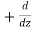
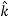
Note that 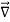 → is not itself a vector – it has to "act upon" a function to create a vector. When it performs this function, the derivatives define vector components which are conveniently multiplied by the unit vectors.
→ is not itself a vector – it has to "act upon" a function to create a vector. When it performs this function, the derivatives define vector components which are conveniently multiplied by the unit vectors.
Where ∇ is called “del” or sometimes “nabla” (after an ancient Hebrewharp of similar shape).With this notation, the relation between force and potential energy can be written
F=−∇V
When ∇ operates on a scalar to give a vector, the combination ∇U is called the gradient of U, sometimes written grad U.
On spherical coordinates, the gradient of a general function V is:
 V =
V = 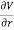 er +
er + 
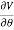 eθ +
eθ +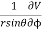 eϕ
eϕ
If V(r,θ,ϕ) only depends on r, that is V=V(r), which is exactly the case of the gravitational potential, then the partial derivatives with respect to θ and ϕ are zero, and therefore the ∇ resumes to:
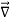 V =
V = 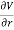 er
er
Key Takeaways
- The potential energy V is equal to the work you must do to move an object from the V=0 reference point to the position r.
- The force on an object is the negative of the derivative of the potential function V. This means it is the negative of the slope of the potential energy curve.
- To find the force in three-dimensions, this derivative of the potential becomes the gradient of the potential,
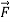 =−
=−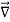 V =
V =
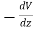
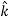
- ∇ is called “del” or sometimes “nabla”
3.6.1 EQUIPOTENTIAL SURFACES
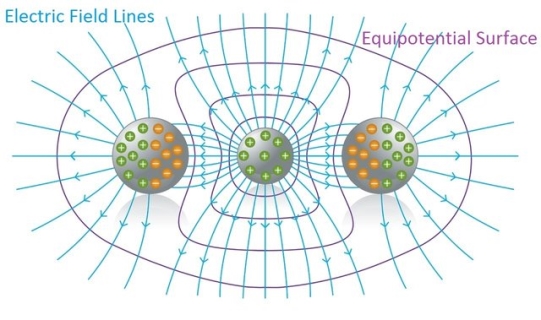
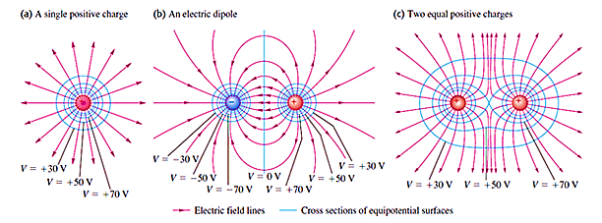
We already studied about Electric field lines help us to understand electric fields, because they give us a "visual" representation of an Electric field. Each of those lines represents the "direction" of the electric field, because the electric field (vector) is tangent to each point of those lines.
In a similar way, the potential at points inside of an electric field can be represented "graphically" using equipotential surfaces.
An Equipotential surface is a surface where the potential is the same (equal) for any point on top of that surface.
In an area where an electric field exists we can construct an equipotential surface that passes through any point. In the diagrams we only show some equipotential lines, mostly with the same potential difference between neighbouring surfaces. And lasty, no point can have two or more different potentials and so equipotential lines can never be tangent and can never intersect.
|
Figure 15: Equipotential surface
NEED OF EQUIPOTENTIAL SURFACES
When moving "along" an equipotential surface the potential is the same for any point where a test charge passes by. Which means that the electric field E doesn't produce Work to the test charge on top of an equipotential surface. More specifically the electric field E can't have a vector component tangent to that surface, so that this component can produce Work to the motion of the moving charge on top of the surface.
So, the electric field is vertically across to any point of the equipotential surface and to the equipotential surface as a whole. Something which gets us to the conclusion that Electric field lines and Equipotential surfaces are always vertically across to each other.
Generally, electric field lines are curved lines and equipotential surfaces are curved surfaces. In the special case of a uniform field where the electric field lines are parallel to each other, the equipotential surfaces are parallel surfaces vertically across to the electric field's lines.
|
Figure 16: Cross Sections of equipotential surfaces (blue lines) and electric field lines (red lines) for assemblies of point charges. There are equal potentials differences between adjacent surfaces.
When the charges inside of a conductor are not moving (are at "rest") then the electric field directly outside of the conductor must be vertically across to every point on top of it's surface.
Of course the electric field E = 0 in every point inside of the conductor (electrostatics), cause else the charges would be moving. This means that the component of E that is tangent to the surface, inside of the conductor, is zero at every point. Therefore the tangent component of E directly outside of the conductor is also zero. If that was not true then we would violate the laws of electrostatics. And so, the electric field is vertically across to every point of the conductor's surface. As a result, a conductive surface is always an equipotential surface.
When the charges inside of a conductor are not moving (are at "rest") then the electric field directly outside of the conductor must be vertically across to every point on top of it's surface.
Of course the electric field E = 0 in every point inside of the conductor (electrostatics), cause else the charges would be moving. This means that the component of E that is tangent to the surface, inside of the conductor, is zero at every point. Therefore the tangent component of E directly outside of the conductor is also zero. If that was not true then we would violate the laws of electrostatics. And so, the electric field is vertically across to every point of the conductor's surface. As a result an conductive surface is always an equipotential surface.
So we concluded that any surface over which the potential is constant is called an equipotential surface. In other words, the potential difference between any two points on an equipotential surface is zero. No work is required to move a charge from one point to another on the equipotential surface. In other words, any surface with the same electric potential at every point is termed as an equipotential surface.
Equipotential Points: If the points in an electric field are all at the same electric potential, then they are known as the equipotential points. If these points are connected by a line or a curve, it is known as an equipotential line. If such points lie on a surface, it is called an equipotential surface. Further, if these points are distributed throughout a space or a volume, it is known as an equipotential volume.
WORK DONE IN EQUIPOTENTIAL SURFACE
The work done in moving a charge between two points in an equipotential surface is zero. If a point charge is moved from point VA to VB, in an equipotential surface, then the work done in moving the charge is given by
W = q0(VA –VB)
As VA – VB is equal to zero, the total work done is W = 0.
Some important properties of equipotential surfaces:
- Work done in moving a charge over an equipotential surface is zero.
- The electric field is always perpendicular to an equipotential surface.
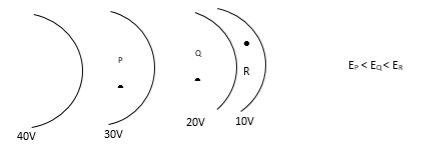
- The spacing between equipotential surfaces enables us to identify regions of strong and weak fields.
- Two equipotential surfaces can never intersect. If two equipotential surfaces could intersect, then at the point of intersection there would be two values of electric potential which is not possible.
- For a point charge, the equipotential surfaces are concentric spherical shells.
- For a uniform electric field, the equipotential surfaces are planes normal to the x-axis
- The direction of the equipotential surface is from high potential to low potential.
- Inside a hollow charged spherical conductor the potential is constant. This can be treated as equipotential volume. No work is required to move a charge from the centre to the surface.
- For an isolated point charge, the equipotential surface is a sphere. i.e. concentric spheres around the point charge are different equipotential surfaces.
- In a uniform electric field, any plane normal to the field direction is an equipotential surface.
- The spacing between equipotential surfaces enables us to identify regions of a strong and weak field i.e. E= −dV/dr ⇒ E ∝ 1/dr
|
Figure 17: Spacing between equipotential surfaces
3.6.2 GRADIENT
The gradient is a fancy word for derivative, or the rate of change of a function. It’s a vector (a direction to move) that
- Points in the direction of greatest increase of a function
- Is zero at a local maximum or local minimum (because there is no single direction of increase)
The term "gradient" is typically used for functions with several inputs and a single output (a scalar field). Yes, you can say a line has a gradient (its slope), but using "gradient" for single-variable functions is unnecessarily confusing. Keep it simple.
“Gradient” can refer to gradual changes of colour, but we’ll stick to the math definition. You’ll see the meanings are related.
PROPERTIES OF THE GRADIENT
Now that we know the gradient is the derivative of a multi-variable function, let’s derive some properties.
The regular, plain-old derivative gives us the rate of change of a single variable, usually x. For example, dF/dx tells us how much the function F changes for a change in x. But if a function takes multiple variables, such as x and y, it will have multiple derivatives: the value of the function will change when we “wiggle” x (dF/dx) and when we wiggle y (dF/dy).
We can represent these multiple rates of change in a vector, with one component for each derivative. Thus, a function that takes 3 variables will have a gradient with 3 components:
- F(x) has one variable and a single derivative: dF/dx
- F(x,y,z) has three variables and three derivatives: (dF/dx, dF/dy, dF/dz)
The gradient of a multi-variable function has a component for each direction.
And just like the regular derivative, the gradient points in the direction of greatest increase.
However, now that we have multiple directions to consider (x, y and z), the direction of greatest increase is no longer simply “forward” or “backward” along the x-axis, like it is with functions of a single variable.
If we have two variables, then our 2-component gradient can specify any direction on a plane. Likewise, with 3 variables, the gradient can specify and direction in 3D space to move to increase our function.
Gradient tells you how much something changes as you move from one point to another (such as the pressure in a stream). The gradient is the multidimensional rate of change of a particular function. The gradient vector is a representative of such vectors which present the value of differentiation in all the 360° direction for the given point on the curve”
The gradient is a vector function which operates on a scalar function to produce a vector whose scale is the maximum rate of change of the function at the point of the gradient and which is pointed in the direction of that utmost rate of change. The symbol for the gradient is ∇.
|
Figure 18: Gradient
(i) A gradient of a scalar quantity is a Vector quantity.
(ii) The magnitude of that vector quantity is equal to the Maximum rate of change of that scalar quantity.
(iii) Change of scalar quantity does not depend only on the coordinate of the point, but also on the direction along which the change is shown.
For the gradient of a vector field, you can think of it as the gradient of each component of that vector field individually, each of which is a scalar. The gradient always points in the direction of the maximum rate of change in a field.
PHYSICAL SIGNIFICANCE OF GRADIENT
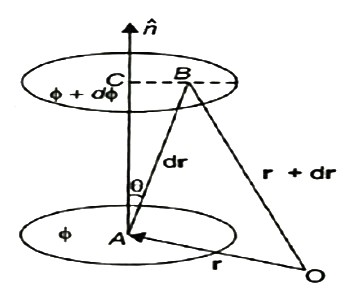
A scalar field may be represented by a series of level surfaces each having a stable value of scalar point function θ. The θ changes by a stable value as we move from one surface to another. These surfaces are known as Gaussian surfaces. Now let the two such surfaces are very close together, be represented by two scalar point functions and (θ + d θ). Let ‘r’ and (r + d θ) be the position vectors of points A and B, on the surfaces θ and (θ + d θ) correspondingly with respect to an origin 0 as shown in Figure 19. Clearly, the vector AB will be dr. Let the least detachment between the two surfaces ‘dn’ be in the direction of unit usual vector n at A.
|
Figure 19: Physical significance of gradient
dn = dr cos θ
= | n | dr | cos θ =n .dr
Dϕ = ∂ϕ/ dn =∂ϕ/dn n .dr…… (1)
Since the continuous scalar function defining the level surfaces (Gaussian surfaces) has a value θ at point A (x, y, z) and (θ + dθ) at point (x + dx, y + dy, z + dz), we have
dϕ = ∂ ϕ/dx dx +dϕ/∂y + ∂ϕ/∂x dz
= (I ∂ϕ/∂x +j ∂ϕ/vy +k ∂ϕ/∂z) .(idx +jdy +kdz)
= ∆ ϕ. dr … … (2)
From equations (1) and (2), equating the values of d θ,
We obtain ∆θ .dr =∆ ϕ= ∂ϕ/ ∂n n .dr
As dr is an arbitrary vector, we have
∆ϕ =∂ϕ/∂ n
Grad ϕ = ∂ ϕ/∂n n
Therefore, the gradient an of a scalar field at any point is a vector field, the scale of which is equal to the highest rate of increase of θ at that point and the direction of it is similar as that of usual to the level surface at that point.
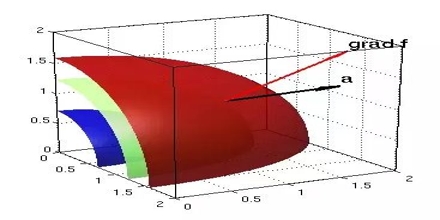
Its physical significance of grad can be understand in terms of the graph of some function z = f(x, y), where f is a reasonable function – say with continuous first partial derivatives. In this case we can think of the graph as a surface whose points have variable heights over the xy – plane. An illustration is given below.
|
Figure 20: Graph of a surface whose points have variable heights over the xy – plane.
If, say, we place a marble at some point (x, y) on this graph with zero initial force, its motion will trace out a path on the surface, and in fact it will choose the direction of steepest descent. This direction of steepest descent is given by the negative of the gradient of f. One takes the negative direction because the height is decreasing rather than increasing.
Using the language of vector fields, we may restate this as follows: For the given function f(x, y), gravitational force defines a vector field F over the corresponding surface z = f(x, y), and the initial velocity of an object at a point (x, y) is given mathematically by –∇f(x, y). The gradient also describes directions of maximum change in other contexts. For example, if we think off as describing the temperature at a point(x, y), then the gradient gives the direction in which the temperature is increasing most rapidly.
Key Takeaways
- An Equipotential surface is a surface where the potential is the same (equal) for any point on top of that surface.
- No work is required to move a charge from one point to another on the equipotential surface.
- The gradient is a fancy word for derivative, or the rate of change of a function. It’s a vector (a direction to move) that Points in the direction of greatest increase of a function and it is zero at a local maximum or local minimum (because there is no single direction of increase)
- A gradient of a scalar quantity is a Vector quantity.
- the gradient an of a scalar field at any point is a vector field, the scale of which is equal to the highest rate of increase of θ at that point and the direction of it is similar as that of usual to the level surface at that point.
- Grad ϕ = ∂ ϕ/∂n n
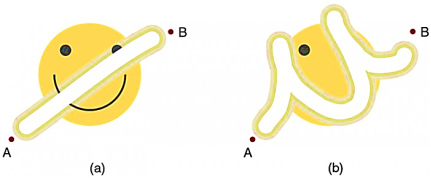
A conservative force may be defined as one for which the work done in moving between two points A and B is independent of the path taken between the two points. The implication of "conservative" in this context is that you could move it from A to B by one path and return to A by another path with no net loss of energy - any closed return path to A takes net zero work.
A further implication is that the energy of an object which is subject only to that conservative force is dependent upon its position and not upon the path by which it reached that position. This makes it possible to define a potential energy function which depends upon position only.
A conservative force is a force that does zero work done in a closed path. If only these forces act then the mechanical energy of the system remains conserved. Examples of conservative force: Gravitational force, spring force etc.
On the other hand, non-conservative forces are those forces which cause loss of mechanical energy from the system. In the above case friction is the non-conservative force. But as we know energy can neither be created nor destroyed hence these forces convert mechanical energy into heat, sound, light etc.
Now, Conservative force has one more property that works done by it is independent of the path taken.
Forces are either conservative or non-conservative. Conservative forces we already discussed. A non-conservative force is one for which work depends on the path taken. Friction is a good example of a non-conservative force. As illustrated in Figure 21,
|
Figure 21: Conservative and Non-Conservative Forces
Work done against friction depends on the length of the path between the starting and ending points. Because of this dependence on path, there is no potential energy associated with non-conservative forces. An important characteristic is that the work done by a non-conservative force adds or removes mechanical energy from a system. Friction, for example, creates thermal energy that dissipates, removing energy from the system. Furthermore, even if the thermal energy is retained or captured, it cannot be fully converted back to work, so it is lost or not recoverable in that sense as well.
In Figure 21. The amount of the happy face erased depends on the path taken by the eraser between points A and B, as does the work done against friction. Less work is done and less of the face is erased for the path in (a) than for the path in (b). The force here is friction, and most of the work goes into thermal energy that subsequently leaves the system (the happy face plus the eraser). The energy expended cannot be fully recovered.
How Non-conservative Forces Affect Mechanical Energy
Mechanical energy may not be conserved when non-conservative forces act. For example, when a car is brought to a stop by friction on level ground, it loses kinetic energy, which is dissipated as thermal energy, reducing its mechanical energy. F
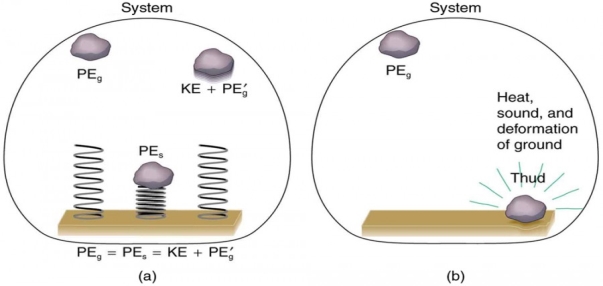
igure 22 compares the effects of conservative and non-conservative forces. We often choose to understand simpler systems such as that described in Figure 22a first before studying more complicated systems as in Figure 22b.
|
22 Figure: Comparison of the effects of conservative and non-conservative forces on the mechanical energy of a system.
In the above figure (a), A system with only conservative forces. When a rock is dropped onto a spring, its mechanical energy remains constant (neglecting air resistance) because the force in the spring is conservative. The spring can propel the rock back to its original height, where it once again has only potential energy due to gravity.
Whereas (b) A system with non-conservative forces. When the same rock is dropped onto the ground, it is stopped by non-conservative forces that dissipate its mechanical energy as thermal energy, sound, and surface distortion. The rock has lost mechanical energy.
Applying Energy Conservation with Non-conservative Forces
When no change in potential energy occurs, applying KEi + PEi + Wnc = KEf + PEf amounts to applying the work-energy theorem by setting the change in kinetic energy to be equal to the net work done on the system, which in the most general case includes both conservative and non-conservative forces. But when seeking instead to find a change in total mechanical energy in situations that involve changes in both potential and kinetic energy, the previous equation KE i + PEi + Wnc = KEf + PEf says that you can start by finding the change in mechanical energy that would have resulted from just the conservative forces, including the potential energy changes, and add to it the work done, with the proper sign, by any non-conservative forces involved.
Let us understand the concept of forces by some examples
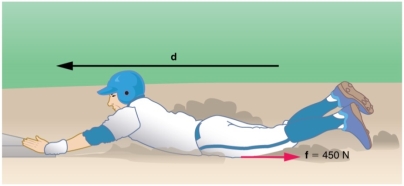
Example1 Calculating Distance Travelled: How Far a Baseball Player Slides
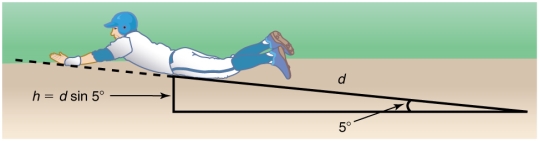
Consider the situation shown in Figure 23, where a baseball player slides to a stop on level ground. Using energy considerations, calculate the distance the 65.0-kg baseball player slides, given that his initial speed is 6.00 m/s and the force of friction against him is a constant 450 N.
|
Figure 23: The baseball player slides to a stop in a distance d. In the process, friction removes the player’s kinetic energy by doing an amount of work equal to the initial kinetic energy.
Solution:
Friction stops the player by converting his kinetic energy into other forms, including thermal energy. the work done by friction, which is negative, is added to the initial kinetic energy to reduce it to zero. The work done by friction is negative, because f is in the opposite direction of the motion (that is, θ = 180º, and so cos θ = −1). Thus Wnc = −fd. The equation simplifies to
 mvi2−fd=0
mvi2−fd=0
or
fd=  mvi2
mvi2
Solving the previous equation for d and substituting known values yields
d= 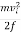 ==
== 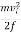
d =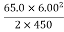 =2.60 m
=2.60 m
The most important point of this example is that the amount of non-conservative work equals the change in mechanical energy. For example, you must work harder to stop a truck, with its large mechanical energy, than to stop a mosquito.
Example 2: Calculating Distance Travelled: Sliding Up an Incline
Suppose that the player from Example 1 is running up a hill having a 5.00º incline upward with a surface similar to that in the baseball stadium. The player slides with the same initial speed. Determine how far he slides.
|
Figure 24: The same baseball player slides to a stop on a 5.00º slope.
Solution
In this case, the work done by the non-conservative friction force on the player reduces the mechanical energy he has from his kinetic energy at zero height, to the final mechanical energy he has by moving through distance d to reach height h along the hill, with h = d sin 5.00º.
This is expressed by the equation KE + PEi + Wnc = KE f + PEf.
The work done by friction is again Wnc = −fd;
Initially the potential energy is PEi = mg · 0 = 0
and the kinetic energy is KEi= mvi2
mvi2
; the final energy contributions are KEf = 0 for the kinetic energy
and PEf = mgh = mgd sin θ for the potential energy.
Substituting these values gives
 mvi2 +0+(−fd)=0+mgdsinθ
mvi2 +0+(−fd)=0+mgdsinθ
Solve this for d to obtain
d = 
d =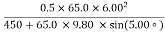 =2.31 m
=2.31 m
As might have been expected, the player slides a shorter distance by sliding uphill. Note that the problem could also have been solved in terms of the forces directly and the work energy theorem, instead of using the potential energy. This method would have required combining the normal force and force of gravity vectors, which no longer cancel each other because they point in different directions, and friction, to find the net force. You could then use the net force and the network to find the distance d that reduces the kinetic energy to zero. By applying conservation of energy and using the potential energy instead, we need only consider the gravitational potential energy mgh, without combining and resolving force vectors. This simplifies the solution considerably.
Key Takeaways
- A conservative force may be defined as one for which the work done in moving between two points A and B is independent of the path taken between the two points.
- A conservative force is a force that does zero work done in a closed path.
- Non-conservative forces are those forces which cause loss of mechanical energy from the system.
- Mechanical energy may not be conserved when non-conservative forces act.
Circulation is the amount of force that pushes along a closed boundary or path. It's the total "push" you get when going along a path, such as a circle.
A vector field is usually the source of the circulation. If you had a paper boat in a whirlpool, the circulation would be the amount of force that pushed it along as it went in a circle. The more circulation, the more pushing force you have.
Curl is simply the circulation per unit area, circulation density, or rate of rotation (amount of twisting at a single point). Imagine shrinking your whirlpool down smaller and smaller while keeping the force the same: you'll have a lot of power in a small area, so will have a large curl. If you widen the whirlpool while keeping the force the same as before, then you'll have a smaller curl. And of course, zero circulation means zero curl.
Circulation is the amount of "pushing" force along a path. Curl is the amount of pushing, twisting, or turning force when you shrink the path down to a single point.
Let's use water as an example. Suppose we have a flow of water and we want to determine if it has curl or not: is there any twisting or pushing force? To test this, we put a paddle wheel into the water and notice if it turns (the paddle is vertical, sticking out of the water like a revolving door -- not like a paddlewheel boat):
If the paddle does turn, it means this field has curl at that point. If it doesn't turn, then there's no curl.
What does it really mean if the paddle turns? Well, it means the water is pushing harder on one side than the other, making it twist. The larger the difference, the more forceful the twist and the bigger the curl.
Also, a turning paddle wheel indicates that the field is "uneven" and not symmetric; if the field were even, then it would push on all sides equally and the paddle wouldn't turn at all.
|
Figure 25: Curl of a force field
The fact that there is a "twist" means the field is not conservative.
A conservative field is "fair" in the sense that work needed to move from point A to point B, along any path, is the same. For example, consider a river: its field is conservative. Sure, you can get a free ride downstream, but then you have to do work to get back to your starting point. Or, you can do work to move upstream, and get a free ride back. Either way, the amount of work you "put in" is the same as what you get back.
However, in a field with curl (like a whirlpool), you can get a free ride by moving in the direction of the twist. In a whirlpool, you can get a free trip by moving with the current in a circle. If you fight the current and go the wrong way, you have to use energy with no free ride at all.
Conservative fields have zero curl: there are no free twists to push you along. Alternatively, if a field has curl, it is not conservative.
Gravity is another example of a conservative field. Technically, if you lift a rock and then let it fall, the energy you get from falling is the same as what you put in to lift the rock. Theoretically speaking, no energy was gained or lost in this transaction.
Mathematically
Curl is a vector, which means it has a both a magnitude and a direction. The magnitude is simply the amount of twisting force at a point.
By convention alone, if the paddle wheel is rotating counter clockwise, its curl vector points out of the page. This is a type of right-hand rule: make a fist with your right hand and stick out your thumb. If the circulation/pushing force follows the twisting of your fingers (counter clockwise), then the curl vector will be in the direction of your thumb.
The force vector is defined by the field we are in. No derivatives or other changes are necessary -- every point in the field has some force acting on it.
t's important to understand why we aren't using the position vector itself -- it tells us where we are, but not where we're going. We need to know our direction to see how much "push" we are getting: Knowing your position in a river isn't important -- are you going upstream or downstream, and at what angle?
Curl of a field (F) written like this:
Curl (F) = 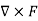
Which is a cross-product of the gradient and the field (F)
|
For the conservative force the curl of that force must be equal to zero
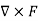 =0
=0
Example: Determine whether or not the following Forces are conservative?
(a) F= 3z2i+ cosyj+ 2xzk
(b)F=ycosxyi+xcosxyj−sinzk
Solution:
(a) F= 3z2i+ cosyj+ 2xzk
For the conservative force the curl of that force must be equal to zero
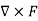 =0
=0
Let us check
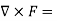

Key Takeaways
- Circulation is the amount of force that pushes along a closed boundary or path.
- Curl is simply the circulation per unit area, circulation density, or rate of rotation (amount of twisting at a single point).
- Curl is a vector, which means it has a both a magnitude and a direction. The magnitude is simply the amount of twisting force at a point.
- For the conservative force the curl of that force must be equal to zero
 =0
=0
Central Forces
The Definition
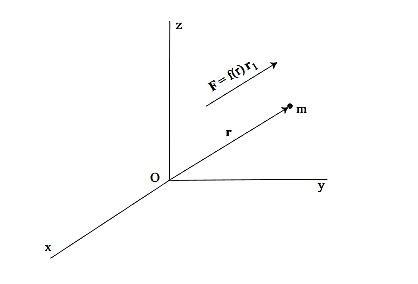
Suppose that force acting on a particle of mass m has the properties that:
•the force is always directed from m toward, or away, from a fixed point O,
•the magnitude of the force only depends on the distance r from O
Forces having these properties are called central forces. The particle is said to move in a central force field.
|
Figure 26: Central Forces
Mathematically, F is a central force if and only if:
F=f(r)r1= f(r)  ………..(1)
………..(1)
Where r1=  is a unit vector in the direction of r.
is a unit vector in the direction of r.
If f(r) <0 the force is said to be attractive towards O. If f(r)>0 the force is said to be repulsive from O.
For example, the gravitational force of attraction between two point masses is a central force. The Coulomb force of attraction and repulsion between charged particles is a central force.
Properties of a Particle Moving under the Influence of a Central Force
If a particle moves in a central force field then the following properties hold:
1. The path of the particle must be a plane curve, i.e., it must lie in a plane.
2. The angular momentum of the particle is conserved, i.e., it is constant in time.
3. The particle moves in such a way that the position vector (from the point O) sweeps out equal areas in equal times. In other words, the time rate of change in area is constant. This is referred to as the Law of Areas.
Equations of Motion for a Particle in a Central Force Field
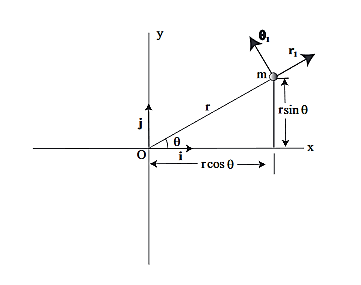
Now we will derive the basic equations of motion for a particle moving in a central force field. From Property 1 above, the motion of the particle must occur in a plane, which we take as the xy plane and the center of force is taken as the origin. In Fig. 2 we show the xy plane, as well as the polar coordinate system in the plane.
|
Figure 27: Polar coordinate system associated with a particle moving in the xy plane.
Since the vectorial nature of the central force is expressed in terms of a radial vector from the origin it is most natural (though not required!) to write the equations of motion in polar coordinates. In earlier lectures we derived the expression for the acceleration of a particle in polar coordinates:
Then, using Newton’s second law, and the mathematical form for the central force given in (1), we have:
These are the basic equations of motion for a particle in a central force field. They will be the starting point for many of our investigations. From these equations we can derive a useful constant of the motion. This is done as follows. From (5) we have:
|
This is an interesting relation that, we will see, is related to properties 2 and 3 above. However, one use for it should be apparent. If you know the r component of the motion it allows you to compute the θ component by integration. This is another example of how constants of the motion allow us to “integrate” the equations of motion. It also explains why constants of the motion are often referred to as integrals of the motion. Now, let us return to property 3 above and derive the Law of Areas
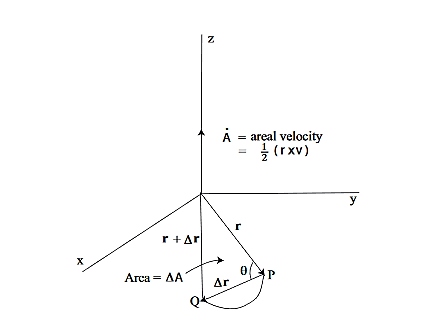
Suppose that in time ∆t the position vector moves from r to r+∆r. Then the area swept out by the position vector in this time is approximately half the area of a parallelogram with sides r and ∆r. We give a proof of this:
Area of parallelogram = height×|r|,=|∆r|sinθ|r|,
=|r×∆r|,
|
Figure 28: Coordinate System
Hence,
∆A= |r×∆r|
|r×∆r|
Dividing this expression by ∆t, and letting ∆t→0, gives:
lim∆t→0
Now we need to evaluate r×v. Using
|
is called the areal velocity.
Alternative Forms to the Basic Equations of Motion for a Particle in a Central Force Field
Recall the basic equations of motion as they will be our starting point:
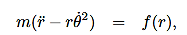 ……….. (8)
……….. (8)
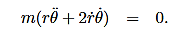 ……….. (9)
……….. (9)
We derived the following constant of the motion:
 ……….. (10)
……….. (10)
This constant of the motion will allow you to determine the θ component of motion, provided you know the r component of motion. However, (8) and (9) are coupled (nonlinear) equations for the r and θ components of the motion. How could you solve them without solving for both the r and θ components? This is where alternative forms of the equations of motion are useful. Let us rewrite (8) in the following form (by dividing through by the mass m):
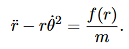 ……….. (11)
……….. (11)
Now, using (10), (11) can be written entirely in terms of r:
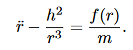 ……….. (12)
……….. (12)
We can use (12) to solve for r(t), and the use (10) to solve for θ(t).Equation (12) is a non-linear differential equation. There is a useful change of variables, which for certain important central forces, turns the equation into a linear differential equation with constant coefficients and these can always be solved analytically. Here we describe this coordinate transformation.
Let r = 
This is part of the coordinate transformation. We will also use θ as a new “time” variable. Coordinate transformation are effected by the chain rule, since this allows us to express derivatives of “old” coordinates in terms of the “new” coordinates. We have:
and
Where, in both expressions, we have used the relation r2
Substituting this relation, along with (14) into (8), gives:
|
Now if f(r) = 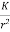 , where K is some constant, (16) becomes a linear, constant coefficient equation
, where K is some constant, (16) becomes a linear, constant coefficient equation
Central Force Fields are Conservative
Now we will show that central forces are conservative forces. We already know that there are many important implications that will follow from this fact, such as conservation of total energy. If a central force is conservative then the work done by the force in moving a particle between two points is independent of the path taken between the two points, i.e., it only depends on the endpoints of the path. In this case we must have
F.dr =-dV
Where V is a scalar valued function (the potential), Evaluating the left-hand-side of this expression gives:
F·dr = f(r) .dr=f(r) dr
.dr=f(r) dr
Also
V(r) =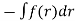 ……….. (17)
……….. (17)
Hence, if we know the central force field, (17) tells us how to compute the potential.
Conservation of Energy for a Particle in a Central Force Field
Since central forces are conservative forces, we know that total energy must be conserved. Now we derive expressions for the total energy of a particle of mass m in a central force field. We will do this in two ways.
First Method
First we compute the kinetic energy. The velocity is given by:
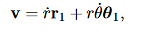
And therefore
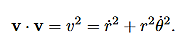
The kinetic energy is given by:
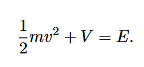
Therefore we have:
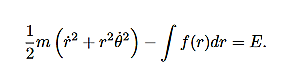 ……….. (18)
……….. (18)
Key Takeaways
- Forces having these properties (i) the force is always directed from m toward, or away, from a fixed point O, (ii) the magnitude of the force only depends on the distance r from O are called central forces.
- The particle is said to move in a central force field.
- If f(r) <0 the force is said to be attractive towards O. If f(r)>0 the force is said to be repulsive from O.
- The path of the particle must be a plane curve, i.e., it must lie in a plane.
- The angular momentum of the particle is conserved, i.e., it is constant in time.
- The particle moves in such a way that the position vector (from the point O) sweeps out equal areas in equal times. In other words, the time rate of change in area is constant. This is referred to as the Law of Areas.
- Areal velocity is given by
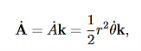
Consider the angular momentum of the reduced mass system L = r × p = r × 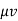 . How does angular momentum L change with time?
. How does angular momentum L change with time?
We have
|
……….(1)
We use the product rule, which is valid for cross products as long as you don’t change the order of the factors. The second term after cross product is zero since ( ×
×  = 0).
= 0).
Recall that r × F which occurs in above expression is called the torque τ. We have shown that in the case of central forces the time derivative of the angular momentum, and hence the torque, are zero. Therefore:
 ……….(2)
……….(2)
i.e. the angular momentum is conserved.
The force F (r) depends only on the distance of the reduced mass from the center of mass and not on the orientation of the system in space. Therefore, this system is spherically symmetric; it is invariant (unchanged) under rotations.
Noether’s theorem states that whenever the laws of physics are invariant under a particular motion or other operation, there will be a corresponding conserved quantity. In this case, we see that the conservation of angular momentum is related to the invariance of the physical system under rotations.
This further can explain as below
Angular momentum: A vector quantity describing an object in circular motion; its magnitude is equal to the momentum of the particle, and the direction is perpendicular to the plane of its circular motion.
Angular momentum is the rotational analog of linear momentum, it is denoted by l, and angular momentum of a particle in rotational motion is defined as:
l = r × p
This is a cross product of r, i.e. the radius of the circle formed by the body in rotational motion, and p, i.e. the linear momentum of the body, the magnitude of a cross product of two vectors is always the product of their magnitude multiplied with the sine of the angle between them, therefore in the case of angular momentum the magnitude is given by,
l = r p sinθ
The law of conservation of angular momentum states that when no external torque acts on an object, no change of angular momentum will occur. For this let us derive relation between torque and angular momentum
Torque and Angular Momentum Relationship
Relationship between torque and angular momentum can found as follows,
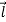 =
= 
Differentiating LHS and RHS,
 =
= 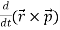
By the property of differentiation on cross products the above expression can be written as follows,
 =
= 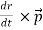 +
+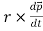
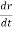 is change in displacement with time, therefore it is linear velocity
is change in displacement with time, therefore it is linear velocity 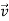
 =
= 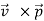 +
+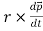
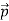 is linear momentum i.e. mass times velocity,
is linear momentum i.e. mass times velocity,
 =
= 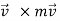 +
+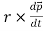
Now notice the first term, there is 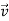 ×
× 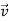 magnitude of cross product is given by
magnitude of cross product is given by
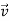 ×
× 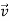 sinθ where the angle is 0 hence the whole term becomes 0.
sinθ where the angle is 0 hence the whole term becomes 0.
From newton’s 2nd law we know that 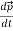 is force,
is force,
 =
= 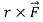
We know that r × F is torque, hence
 =
= 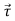 (torque)
(torque)
So rate of change of angular momentum is torque.
Now this statement seems clearer to you; The law of conservation of angular momentum states that when no external torque acts on an object, no change of angular momentum will occur.
The conserved quantity we are investigating is called angular momentum. The symbol for angular momentum is the letter L. Just as linear momentum is conserved when there is no net external force, angular momentum is constant or conserved when the net torque is zero.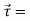

For the situation in which the net torque is zero, 
 =0
=0
If the change in angular momentum Δl is zero, then the angular momentum is constant; therefore,
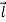 =constant
=constant
(when net τ=0).
This is an expression for the law of conservation of angular momentum.
Example
An example of conservation of angular momentum is seen in an ice skater executing a spin, as shown in figure 29. The net torque on her is very close to zero, because 1) there is relatively little friction between her skates and the ice, and 2) the friction is exerted very close to the pivot point.
|
Figure 29: Conservation of Angular Momentum
Conservation of Angular Momentum: An ice skater is spinning on the tip of her skate with her arms extended. Her angular momentum is conserved because the net torque on her is negligibly small. In the next image, her rate of spin increases greatly when she pulls in her arms, decreasing her moment of inertia. The work she does to pull in her arms results in an increase in rotational kinetic energy.
(Both F and r are small, and so 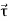 =
= 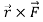 is negligibly small.) Consequently, she can spin for quite some time. She can also increase her rate of spin by pulling in her arms and legs. When she does this, the rotational inertia decreases and the rotation rate increases in order to keep the angular momentum L=Iω constant. (I: rotational inertia, ω: angular velocity)
is negligibly small.) Consequently, she can spin for quite some time. She can also increase her rate of spin by pulling in her arms and legs. When she does this, the rotational inertia decreases and the rotation rate increases in order to keep the angular momentum L=Iω constant. (I: rotational inertia, ω: angular velocity)
Conservation of angular momentum is one of the key conservation laws in physics, along with the conservation laws for energy and (linear) momentum. These laws are applicable even in microscopic domains where quantum mechanics governs; they exist due to inherent symmetries present in nature.
The solar system is another example of how conservation of angular momentum works in our universe. Our solar system was born from a huge cloud of gas and dust that initially had rotational energy. Gravitational forces caused the cloud to contract, and the rotation rate increased as a result of conservation of angular momentum
Key Takeaways
- The angular momentum of the reduced mass system L = r × p = r ×
 .
. - Noether’s theorem states that whenever the laws of physics are invariant under a particular motion or other operation, there will be a corresponding conserved quantity.
- Angular momentum: A vector quantity describing an object in circular motion; its magnitude is equal to the momentum of the particle, and the direction is perpendicular to the plane of its circular motion. It is defined as: l = r × p.
- Relationship between torque and angular momentum can found as follows,
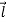 =
= 
References Books
1. Engineering Physics, R.K. Gaur and S.L. Gupta, Dhanapat Rai Publications
2. A Text Book of Engineering Physics, M.N. Avadhanulu, P.G. Kshirsagar, S. Chand and Company Ltd.
3. Engineering Mechanics, 2nd ed.- MK Harbola, Cengage Learning
4. “Introduction to Mechanics”, M.K.Vermas, Universities Press
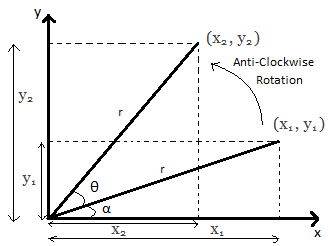
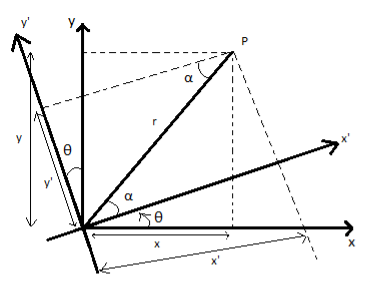
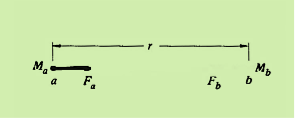


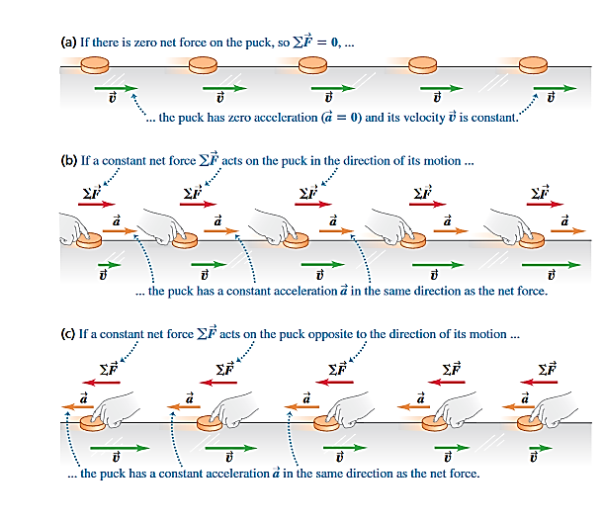
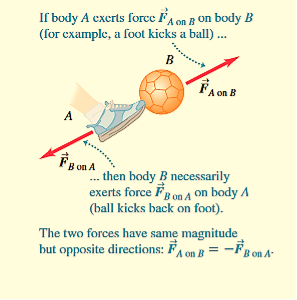
![\includegraphics[width=0.7\textwidth]{ref_frames.eps}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642923664_4631138.png)