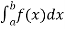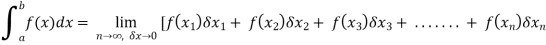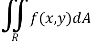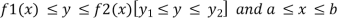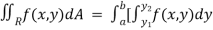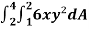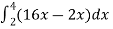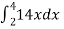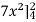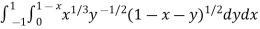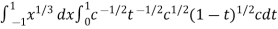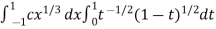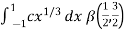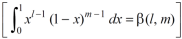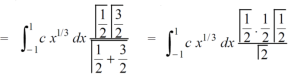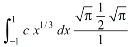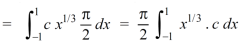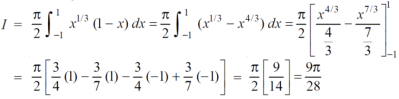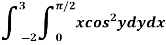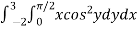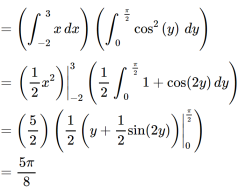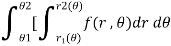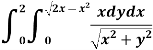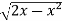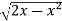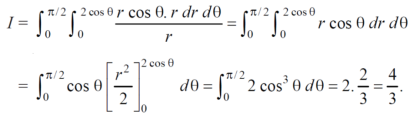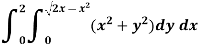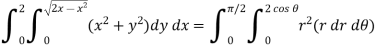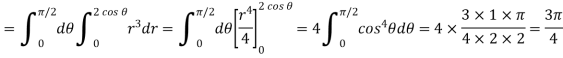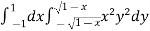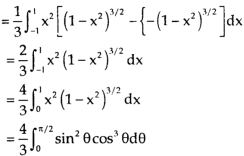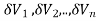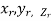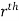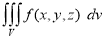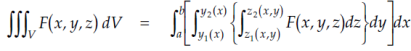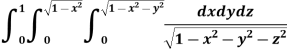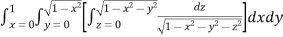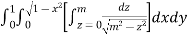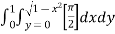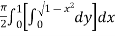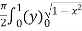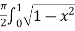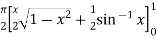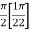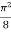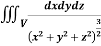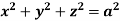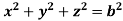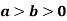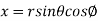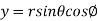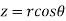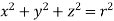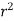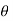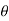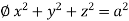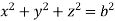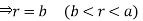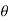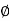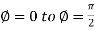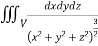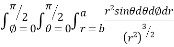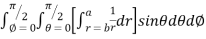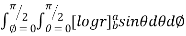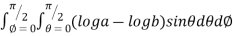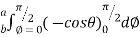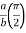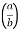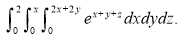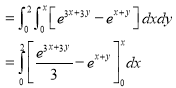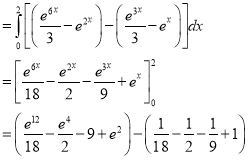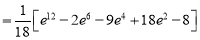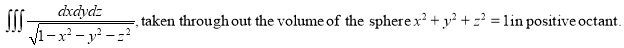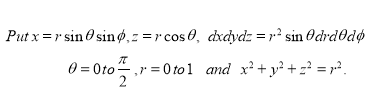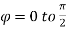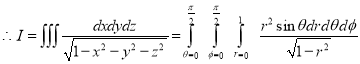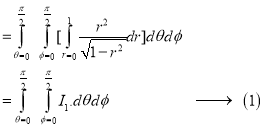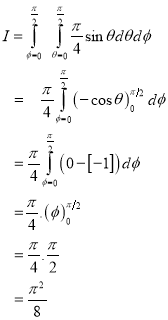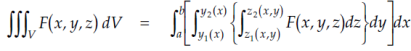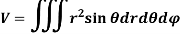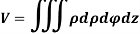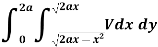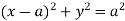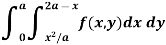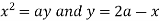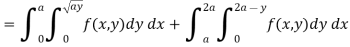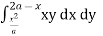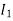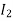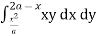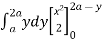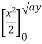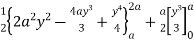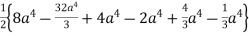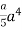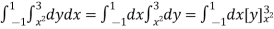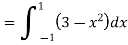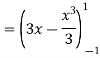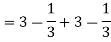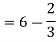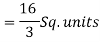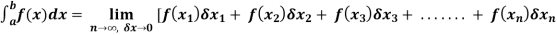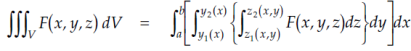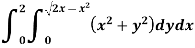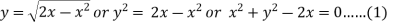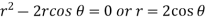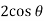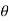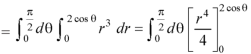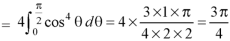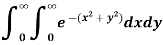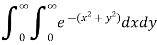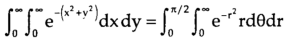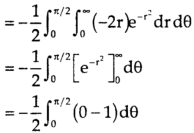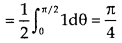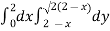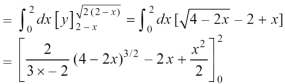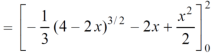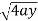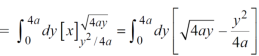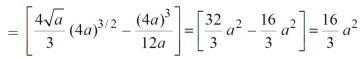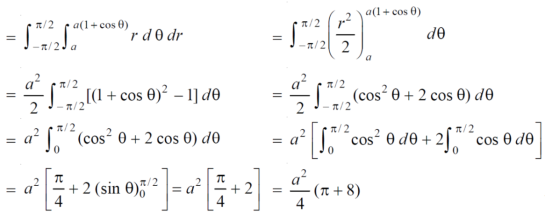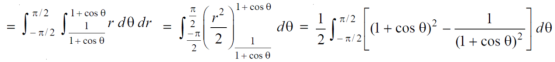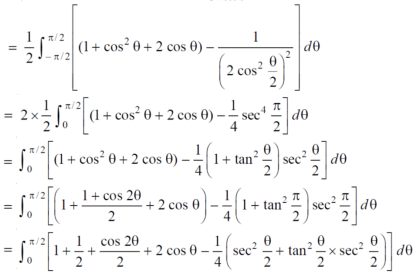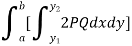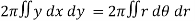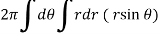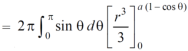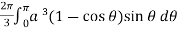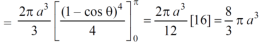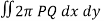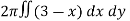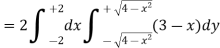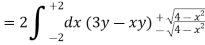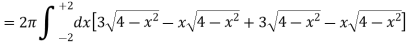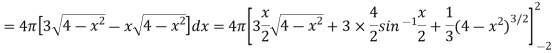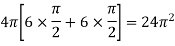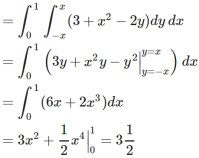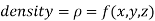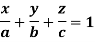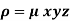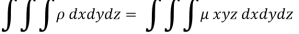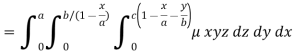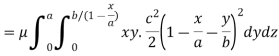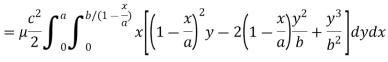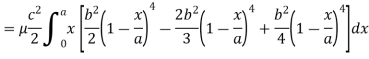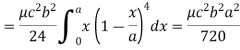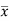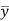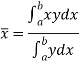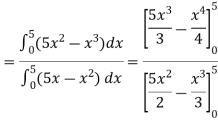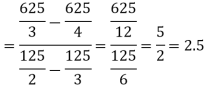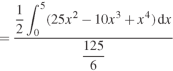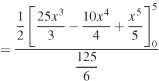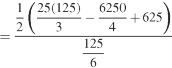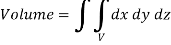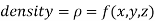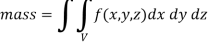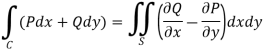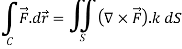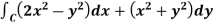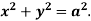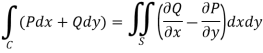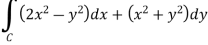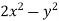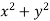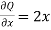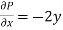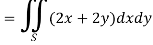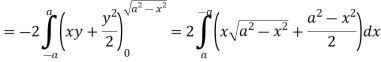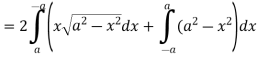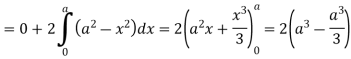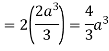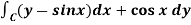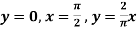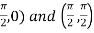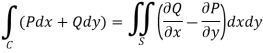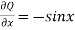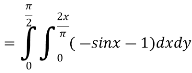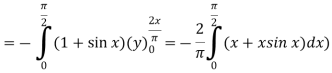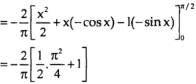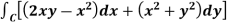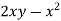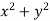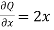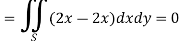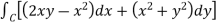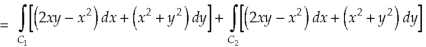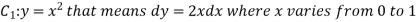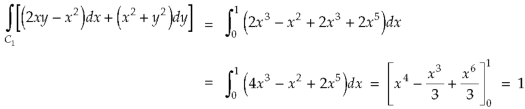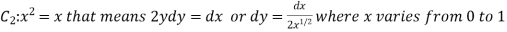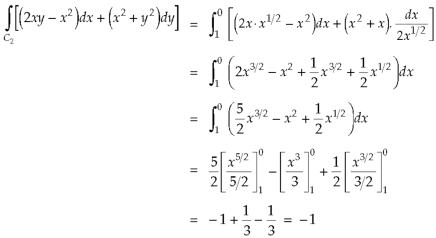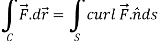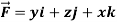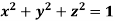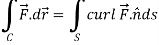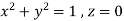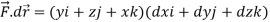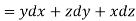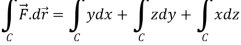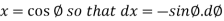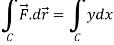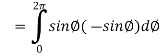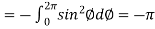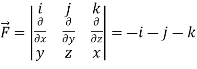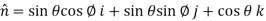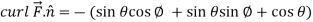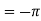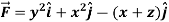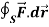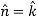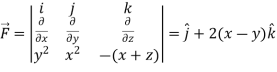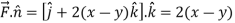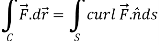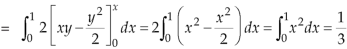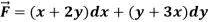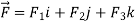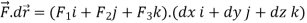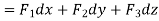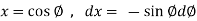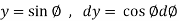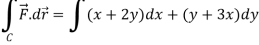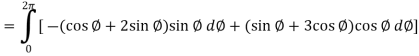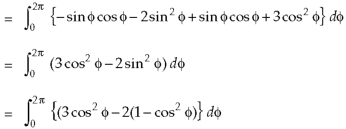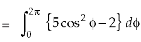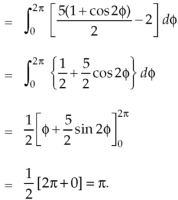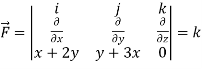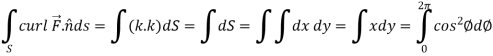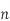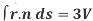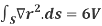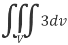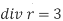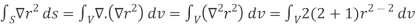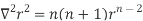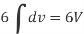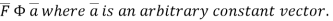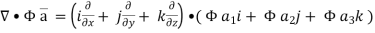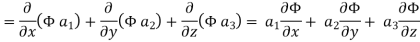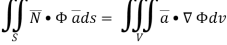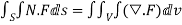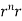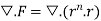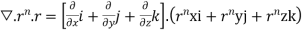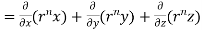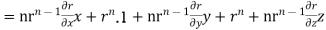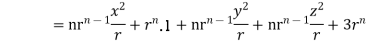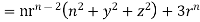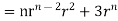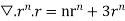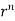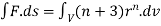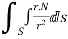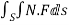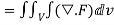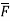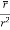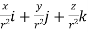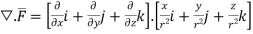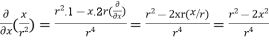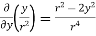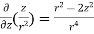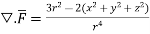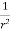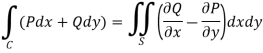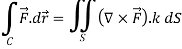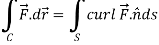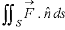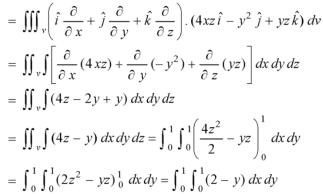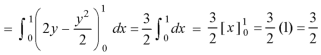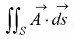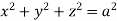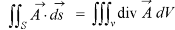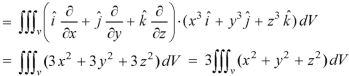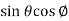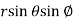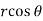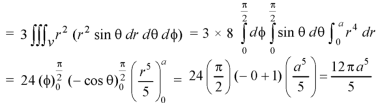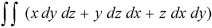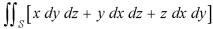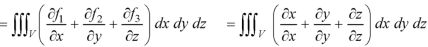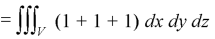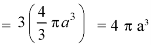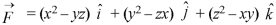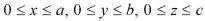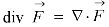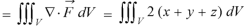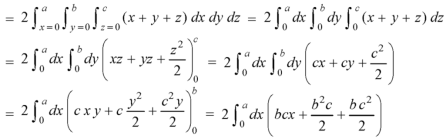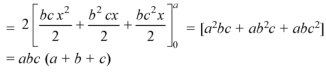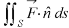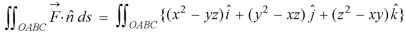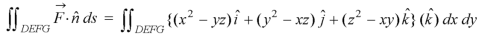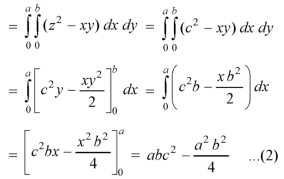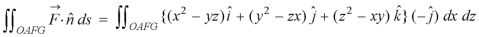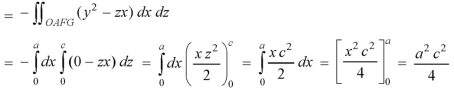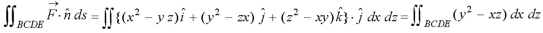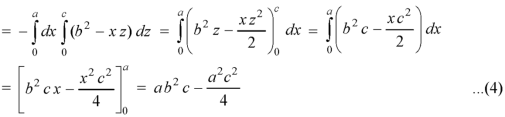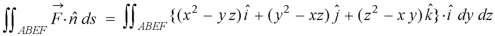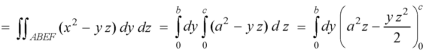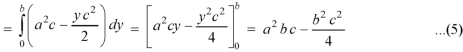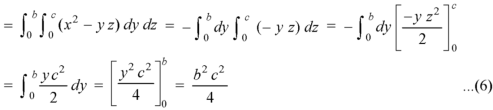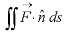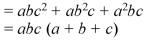Double integral –

Before studying about multiple integrals , first let’s go through the definition of definition of definite integrals for function of single variable.

As we know, the integral

Where is belongs to the limit a ≤ x ≤ b

This integral can be written as follows-

Now suppose we have a function f(x , y) of two variables x and y in two dimensional finite region Rin xy-plane.

Then the double integration over region R can  be evaluated by two successive integration

Evaluation of double integrals-

If A is described as 

Then,

]dx

Let do some examples to understand more about double integration-

Example-: Evaluate , where dA is the small area in xy-plane.

Sol.     Let ,     I = 

                                                       =

                                                      = 

                                                       = 

                                                       =  84 sq. unit.

Which is the required area,

Example-2:  Evaluate

Sol. Let us suppose the integral is I,

                            I =

Put c = 1 – x in I, we get

                           I =

Suppose, y = ct

Then dy = c

now we get,

I =

I =

I =

I =

I  =

 As we know that by beta function,

Which gives,

Now put the value of c, we get

Example-3:  Evaluate the following double integral,

Sol.  Let,

I = 

On solving the integral, we get

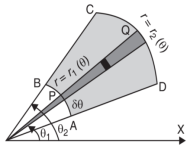
Double integration in polar coordination -

In polar coordinates, we need to evaluate

Over the region bounded by θ1 and θ2.

And the curves r1(θ) and r2(θ)

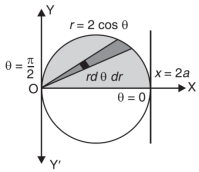
Example-1: Evaluate the following by changing to polar coordinates,

Sol. In this problem, the limits for y are 0 to and the limits for are 0 to 2.

       Suppose,

y =

squaring both sides,

y² = 2x - x²

x² + y² = 2x

but in polar coordinates,

we have,

r² = 2r cosθ

r = 2 cosθ

from the region of integration, r lies from 0 to 2 cosθ  and θ varies from 0  to π / 2.

As we know in case of polar coordinates,

Replace x by r cosθ and y by r sinθ, dy dx by r drdθ,

We get,

Example-2: Evaluate the following integral by converting into polar coordinates.

Sol.  Here limits of y,

y =

y² = 2x - x²

x² + y² = 2x

x² + y² - 2x = 0  ………………(1)

Eq. (1) represent a circle whose radius is 1 and centre is ( 1, 0)

Lower limit of y is zero.

Region of integration in upper half circle,

First we will covert into polar coordinates,

By putting

x by r cos θ and y by r sinθ ,  dy dx by r drdθ,

limits of r are 0 to 2 cosθ  and limits of  θ  are from 0  to π / 2.

Example-3: Evaluate

Sol. Let the integral,

I =

=

Put x = sinθ

= π / 24   ans.

Triple integrals

Definition: Let f(x,y,z) be a function which is continuous at every point of the finite region (Volume V) of three dimensional space. Divide the region V into n sub regions of respective volumes. Let () be a point in the    sub region then the sum:

=

is called triple integration of f(x, y, z) over the region V provided limit on R.H.S of above Equation exists.

Example-1: Evaluate

Solution:

Let

I     =    

=    

                                            (Assuming m =  )

= dxdy

=

=

= dx

=  dx

= 

=

I =

Example-2: Evaluate        Where V is annulus between the spheres  and  ()

Solution:  It is convenient to transform the triple integral into spherical polar co-ordinate by putting

,                      ,   

,    dxdydz = sindrdd,

and

For the positive octant,  r  varies from  r =b to r =a  ,     varies from and     varies from

I= 

= 8

=8

=8

=8

=8 log

= 8 log

I= 8 log

I =  4 log

Example-3: Evaluate

Solution:-

Ex.4: Evaluate-

Solution:-

1. 
2. The volume of solid is given by

Volume =

3.     In Spherical polar system 

4.     In cylindrical polar system

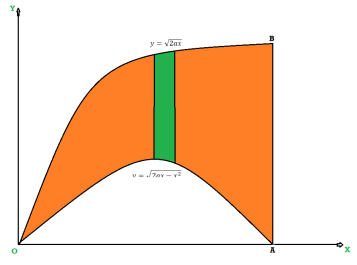
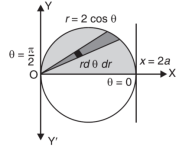
The limits of integration change when we change the order of integration.

We draw the rough diagram of the region of integration to find the new limits.

Example-1: Change the order of integration in the double integral-

Sol.

Limits are given-

x = 0, x = 2a

And

and

The area of integration is the shaded portion of OAB. On changing the order of integration first we will integrate with respect to x, the area of integration has three portions BCE, ODE and ACD,

Now-

Which is the required answer.

Example: Change the order of integration in-

Sol.

The limits are given as-

It means-

Also

Now we have here-

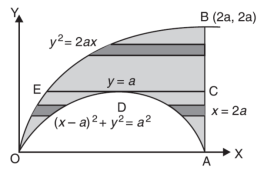
Example-2: Change the order of integration for the integral  and evaluate the same with reversed order of integration.             

Sol:  

 Given,  I  =  …(1)

In the given integration, limits are

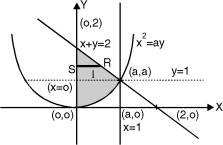
  y = , y = 2a – x and x = 0,   x = a 

The region bounded by x2 = ay, x + y = 2a    Fig.6.5

And x = 0, x = a is as shown in Fig. 6.5

Here we have to change order of Integration. Given the strip is vertical.

Now take horizontal strip SR.

To take total region, Divide region into two parts by taking line y = a.  

1 st Region:

Along strip, y constant and x varies from x = 0 to x = 2a – y. Slide strip IIelto  x-axis therefore y varies from y = a to y = 2a.

        = dyxy dx .....…(2)

2nd Region:

Along strip, y constant and x varies from x = 0 to x= . Slide strip IIel to x-axis therefore x-varies from y = 0 to y = a.

      = dyxy dx    …(3)

From Equation (1), (2) and (3),

   =  dyxy dx + dyxy dx

= +  y dy

=dy  + (ay) dy =  y (4a2 – 4ay + y2) dy +  ay2dy

=  (4a2 y – 4ay2 + y3) dy +   y2dy

= 

= +

=            a4

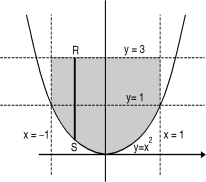
Example-4: Express as single integral and evaluate dy dx + dy dx.

Sol: 

Given: I  =  dy dx + dy dx

  I  =  I1 + I2

The limits of region of integration I1 are
x = – ; x =  and y = 0, y = 1 and I2 are x = – 1,
x = 1 and y = 1, y = 3.

The region of integration are as shown in Fig

To consider the complete region take a vertical strip SR along the strip y varies from y to  y = 3 and x varies from x = –1 to x = 1.

I  =

2.    

Evaluation of double integrals in polar coordinates-

Example: Evaluate-

Sol.

Here we have-

Limits of y-

It represents the circle with centre (1, 0) and radius 1.

Lower limit of y is 0.

Region of integration is upper half circle.

Lets convert the equation (1) into polar coordinates by putting-

X =  rcosθ and y =  r cosθ

Limits of r are 0 to

Limits of are 0 to π/2

Example: Evaluate-

By changing into polar coordinates.

Sol.

We have

The limits of x and y are 0 to

Hence the region of integration is in the first quadrant,

The region is covered by the radius strip from r = 0 to r = ∞ and it starts from θ = 0 to θ = π/2

Hence the integral becomes-

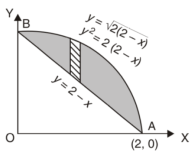
Area of double integration

Area in Cartesian coordinates-

Example-1: Find the area enclosed by two curves using double integration.

                                           y = 2 – x and y² = 2 (2 – x)

Sol.  Let,

                         y =  2 – x  ………………..(1)

and                y² = 2 (2 – x) ………………..(2)

on solving eq. (1) and (2)

we get the intersection points  (2,0) and (0,2) ,

we know that,

                                             Area =

Here we will find the area as below,

                                           Area =

Which gives,

                                                   = ( - 4 + 4 /2 ) + 8 / 3  = 2 / 3.

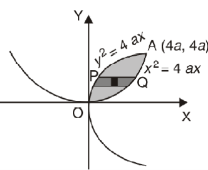
Example-2: Find the area between the parabola y ² = 4ax and another parabola x² = 4ay.

Sol. Let,

y² = 4ax ………………..(1)

and

x² = 4ay…………………..(2)

then if we solve these equations , we get the values of points where these two curves intersect

x varies from y²/4a to and y varies from o to 4a,

now using the conceot of double integral,

Area = 

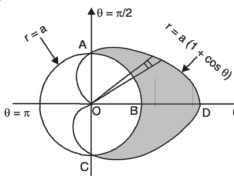
Area in polar coordinates-

Example-3:  Find the area lying inside the cardioid r = a(1+cosθ) and outside the circle r = a, by using double integration.

Sol. We have,

r = a(1+cosθ)   …………………….(1)

and

r = a ……………………………….(2)

on solving these equations by eliminating r , we get

a(1+cosθ)    =   a

(1+cosθ) = 1

cosθ = 0

here a θ varies from – π/2  to    π/2 

limit of r will be a and 1+cosθ)   

Which is the required area.

Example-4: Find the are lying inside a cardioid r = 1 + cosθ and outside the parabola r(1 + cosθ) = 1.

Sol. Let,

r = 1 + cosθ   ……………………..(1)

r(1 + cosθ) = 1……………………..(2)

solving these equations, we get

(1 + cosθ )(1 + cosθ ) = 1

(1 + cosθ )² = 1

1 + cosθ    = 1

cosθ = 0

θ = ±π / 2

so that, limits of r are,

1 + cosθ    and 1 / 1 + cosθ

The area can be founded as below,

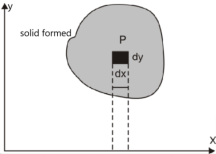
Double integrals as volumes

Suppose we have a curve  y = f(x) is revolved about an axis , then a solid is generated , now we need to find out the volume of the solid generated ,

The formula for volume of the solid generated about x-axis,

Example-1: Calculate the volume generated by the revolution of a cardioid,

r = a ( 1 – cosθ) about its axis

Sol. Here,           

r = a ( 1 – cosθ)

Volume =

=

which is the volume of generated by cardioid.

Example-2: Find the volume generated by revolving a circle x ² + y² = 4 about the line x= 3.

Sol. We know that,

Volume =

Here , PQ = 3 – x,

                                   =

The volume is 24π².

Example-3: Calculate the volume under the surface z = 3 + x² - 2y over the region R defined as 0≤ x ≤ 1 and  -x ≤ y ≤ x

Sol. The is a double integral of  z = 3 + x² - 2y over the region R.

Volume will be,

CENTER OF MASS AND GRAVITY-

Centre of mass-

We have-

Mass = volume

Example: Find the mass of a plate formed by the coordinate planes and the plane-

The variable density

Sol.

Here we the mass will be-

The limits of y are from y = 0 to y = b(1 – x/a) and limits of x are from 0 to a.

Therefore the required mass will be-

Which is the required answer.

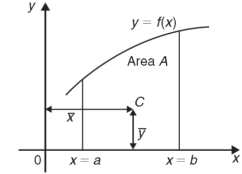
Centre of gravity-

The centre of gravity of a lamina is the point where it balances perfectly which means the lamina’s centre of mass.

If and are the coordinates of the centroid C of area A, then-

And

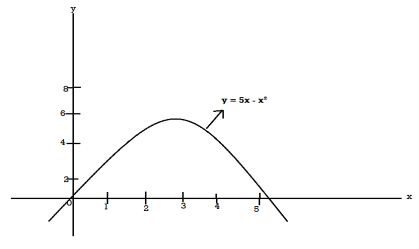
Example: Determine the coordinates of the centroid of the area lying between the curve y = 5x - x² and the x-axis.

Sol.

Here y = 5x - x²when y = 0, x = 0 or x = 5

Therefore the curve cuts the x-axis at 0 and 5 as in the figure-

Now

= 2.5

Therefore the centroid of the area lies at (2.5, 2.5)

1. Centre of mass-

We have-

Mass = volume

Green’s theorem in a plane

If C be a regular closed curve in the xy-plane and S is the region bounded by C then,

Where P and Q are the continuously differentiable functions inside and on C.

Green’s theorem in vector form-

Example-1: Apply Green’s theorem to evaluate where C is the boundary of the area enclosed by the x-axis and the upper half of circle

Sol. We know that by Green’s theorem-

And it it given that-

Now comparing the given integral-

P =   and   Q =

Now-

and

So that by Green’s theorem, we have the following integral-

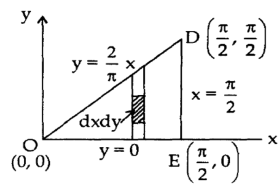
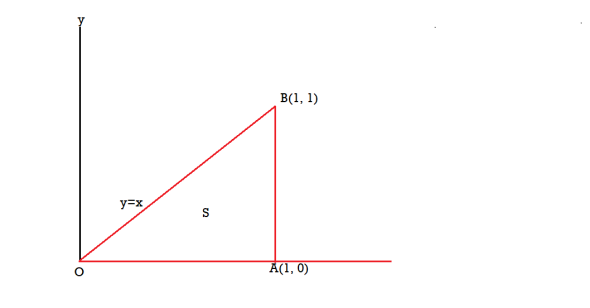
Example-2: Evaluate by using Green’s theorem, where C is a triangle formed by

Sol. First we will draw the figure-

Here the vertices of triangle OED are (0,0), (

Now by using Green’s theorem-

Here P = y – sinx, and Q  =cosx

So that-

and

Now-

=

Which is the required answer.

Example-3: Verify green’s theorem in xy-plane for where C is the boundary of the region enclosed by

Sol.

On comparing with green’s theorem,

We get-

P = and Q =

and

By using Green’s theorem-

  ………….. (1)

And left hand side=

………….. (2)

Now,

Along

Along

Put these values in (2), we get-

               L.H.S. = 1 – 1 = 0

So that the Green’s theorem is verified.

Stoke’s theorem (without proofs) and their verification-

If is any continuously differentiable vector point function and S is a surface bounded by a curve C, then-

Example-1: Verify stoke’s theorem when and surface S is the part of sphere , above the xy-plane.

Sol.

We know that by stoke’s theorem,

Here C is the unit circle-

So that-

Now again on the unit circle C, z = 0

dz = 0

Suppose, 

And           

Now

  ……………… (1)

Now-

                 Curl

Using spherical polar coordinates-

  ………………… (2)

From equation (1) and (2), stoke’s theorem is verified.

Example-2: If and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate by using Stoke’s theorem.

Sol. here we see that z-coordinates of each vertex of the triangle is zero, so that the triangle lies in the xy-plane and

Now,

Curl

Curl

The equation of the line OB is y = x

Now by stoke’s theorem,

Example-3: Verify Stoke’s theorem for the given function-

Where C is the unit circle in the xy-plane.

Sol. Suppose-

Here

We know that unit circle in xy-plane-

Or

So that,

Now

Curl

Now,

Hence the Stoke’s theorem is verified.

Gauss divergence theorem

If V is the volume bounded by a closed surface S and is a vector point function with continuous derivative-

Then it can be written as-

where unit vector to the surface S.

Example-1: Prove the following by using Gauss divergence theorem-

1.

2.

Where S is any closed surface having volume V and

Sol. Here we have by Gauss divergence theorem-

Where V is the volume enclose by the surface S.

We know that-

                                             = 3V

2.

Because 

Example – 2 Show that 

Sol

By divergence theorem,  ..…(1)

Comparing  this  with  the  given  problem  let 

Hence, by (1)

                                    ………….(2)

Now ,

Hence,from (2), Weget,

Example Based on Gauss Divergence Theorem

1. Show that

Soln.  We have Gauss Divergence Theorem

 By data, F=  

  =(n+3)

2 Prove that  =

Soln. By Gauss Divergence Theorem,

 =

= =

  =

1. Green’s theorem in a plane

2.     Green’s theorem in vector form-

3.     Stoke’s theorem

4.     Gauss divergence theorem

Example: Evaluate-

Where

And S is the surface of the cube bounded by x = 0, x = 1, y = 1, z = 0, z = 1.

Sol.

By the Divergence theorem-

Example: By using divergence theorem to evaluate-

Where-

And S is the surface of the sphere .

Sol.

On putting x = , y = , z = , we get-

Example: Use the divergence theorem to evaluate-

Over the surface of a sphere of radius ‘a’.

Sol.

Here we have-

= 3 × Volume of the sphere

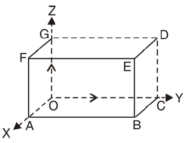
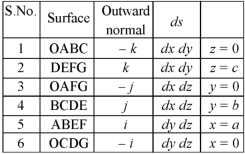
Example: Verify the Gauss divergence theorem for-

Taken over the rectangular parallelopiped

Sol.

We have-

Volume integral-

To evaluate , where S consists of six plane surfaces-

….. (3)

Add 1,2,3,4,5 and 6, we get-

The Gauss divergence theorem is varified.