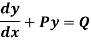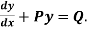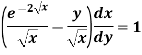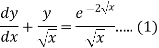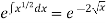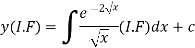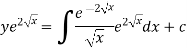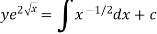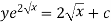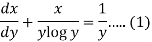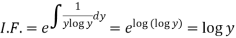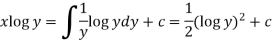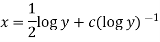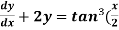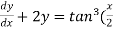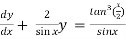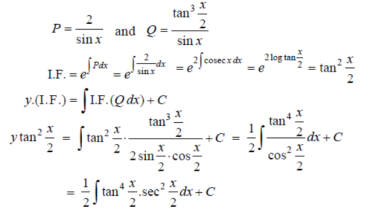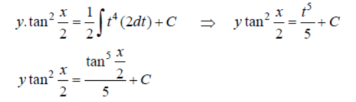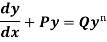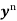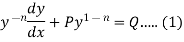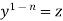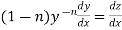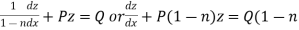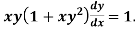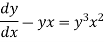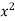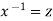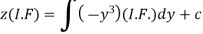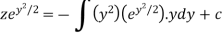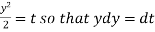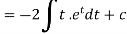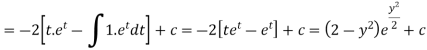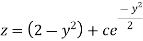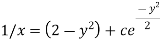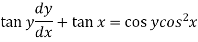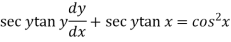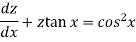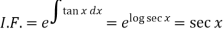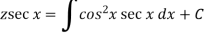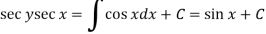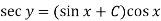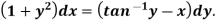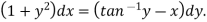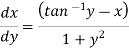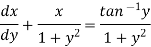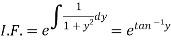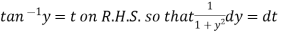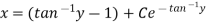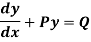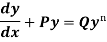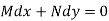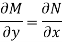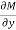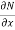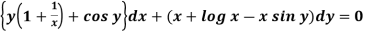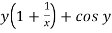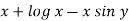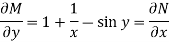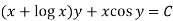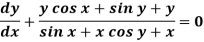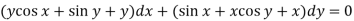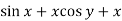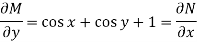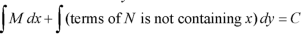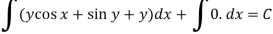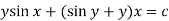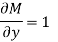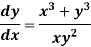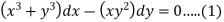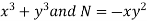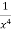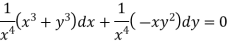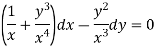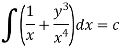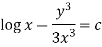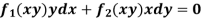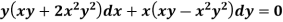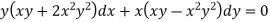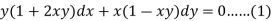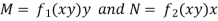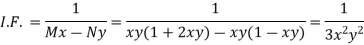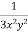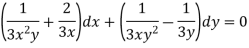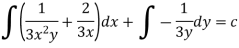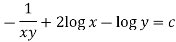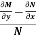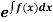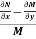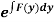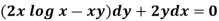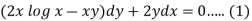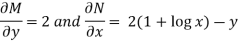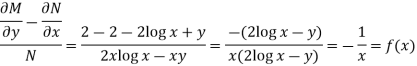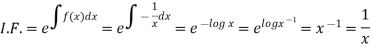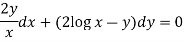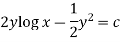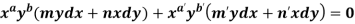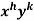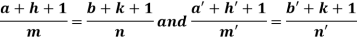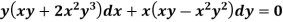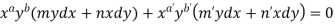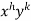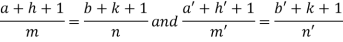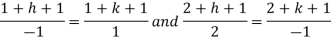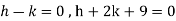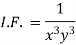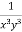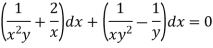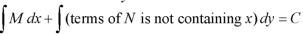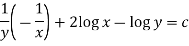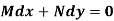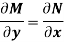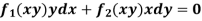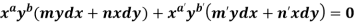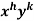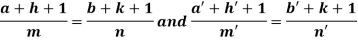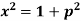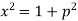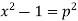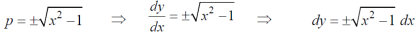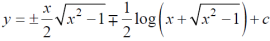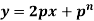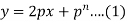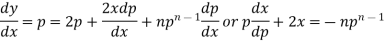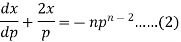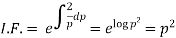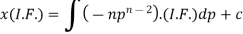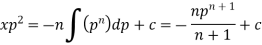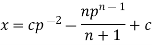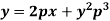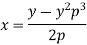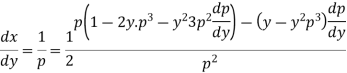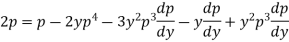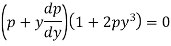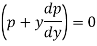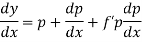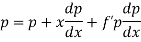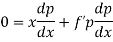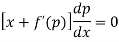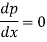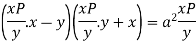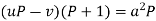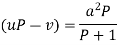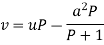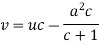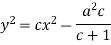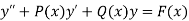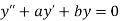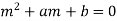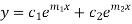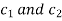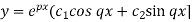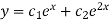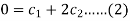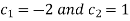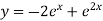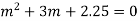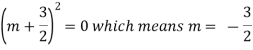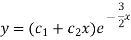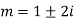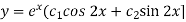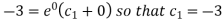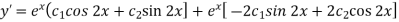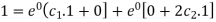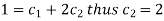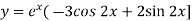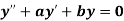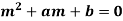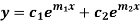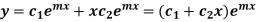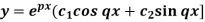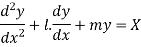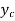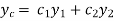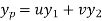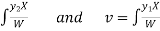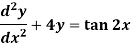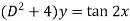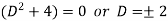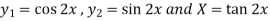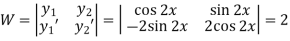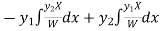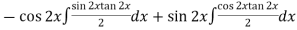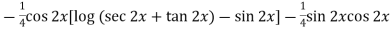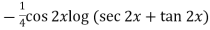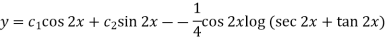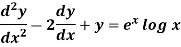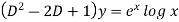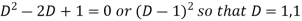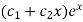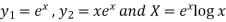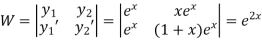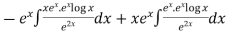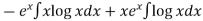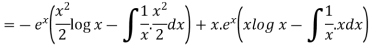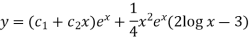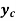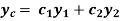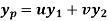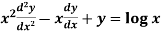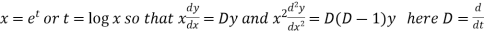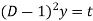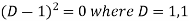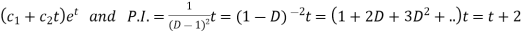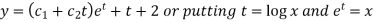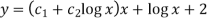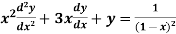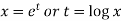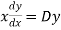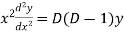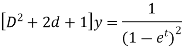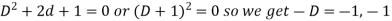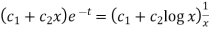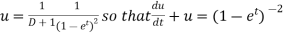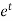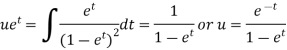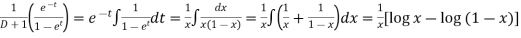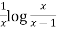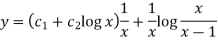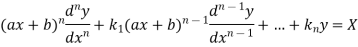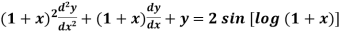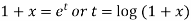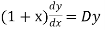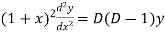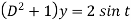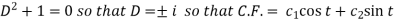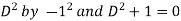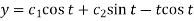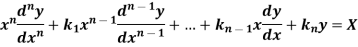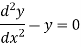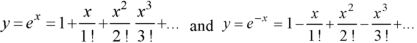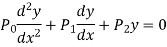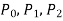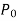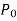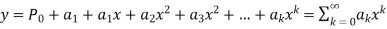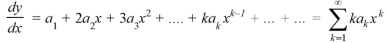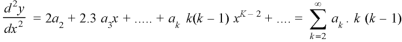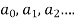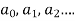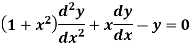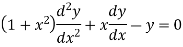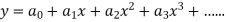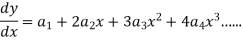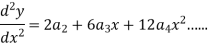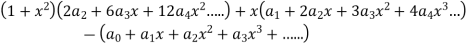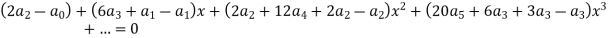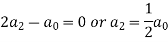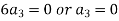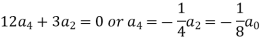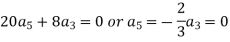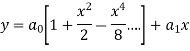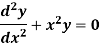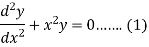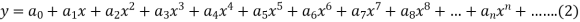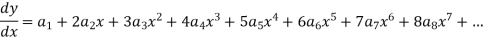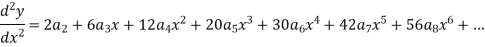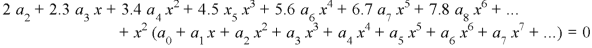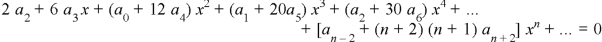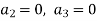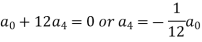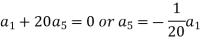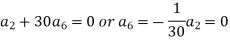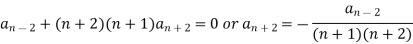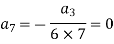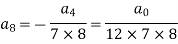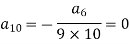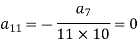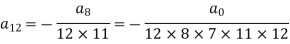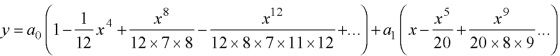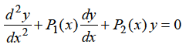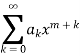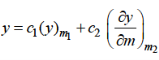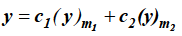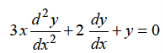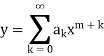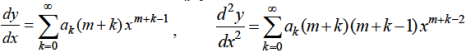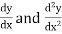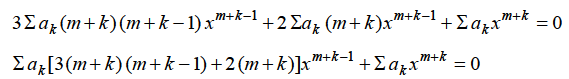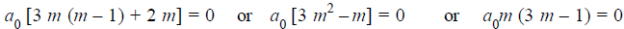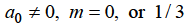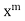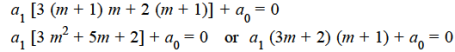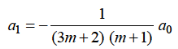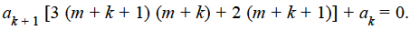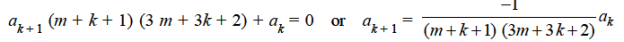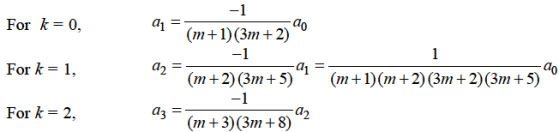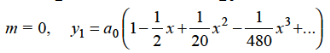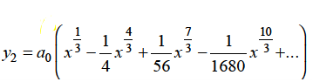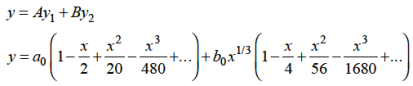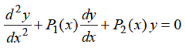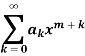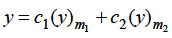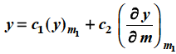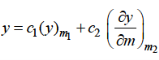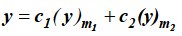A differential equation of the form

Is called linear differential equation.

It is also called Leibnitz’s linear equation.

Here P and Q are the function of x

Working rule

(1)Convert the equation to the standard form  

(2) Find the integrating factor.

(3) Then the solution will be y(I.F) =

Example-1: Solve-

Sol. We can write the given equation as-

So that-

I.F. =

The solution of equation (1) will be-

Or

Or

Or

Example-2: Solve-

Sol.

We can write the equation as-

We see that it is a Leibnitz’s equation in x-

So that-

Therefore the solution of equation (1) will be-

Or

Example-3: Solve sin x )

Solution:  here we have,

sin x )

which is the linear form,

Now,

             Put tan   so that  sec² dx =  dt, we get

 Which is the required solution.

Bernoulli’s equation-

The equation

Is reducible to the Leibnitz’s linear equation and is usually called Bernoulli’s equation.

Working procedure to solve the Bernoulli’s linear equation-

Divide both sides of the equation -
 

By, so that

Put so that

Then equation (1) becomes-

)

Here we see that it is a Leibnitz’s linear equations which can be solved easily.

Example: Solve

Sol.

We can write the equation as-

On dividing by , we get-

Put so that

Equation (1) becomes,

Here,

Therefore the solution is-

Or

Now put

Integrate by parts-

Or
 

Example: Solve

Sol. here given,

Now let z = sec y, so that dz/dx = sec y tan y dy/dx

Then the equation becomes-

Here,

Then the solution will be-

Example: Solve-

Sol. here given-

We can re-write this as-

Which is a linear differential equation-

The solution will be-

Put

1. A differential equation of the form

is called linear differential equation OR Leibnitz’s linear equation.

2.     The equation

called Bernoulli’s equation.

Definition-

An exact differential equation is formed by differentiating its solution directly without any other process,

Is called an exact differential equation if it satisfies the following condition-

Here
is the differential co-efficient of M with respect to y keeping x constant and
is the differential co-efficient of N with respect to x keeping y constant.

Step by step method to solve an exact differential equation-

1. Integrate M w.r.t. x keeping y constant.

2. Integrate with respect to y, those terms of N which do not contain x.

3. Add the above two results as below-

Example-1: Solve

Sol.

Here M = and N =

Then the equation is exact and its solution is-

Example-2: Solve-

Sol. We can write the equation as below-

Here M = and N =

So that-

The equation is exact and its solution will be-

Or

Example-3: Determine whether the differential function ydx –xdy = 0 is exact or not.

Solution.  Here the equation is the form of  M(x , y)dx + N(x , y)dy = 0

   But, we will check for exactness,

These are not equal results, so we can say that the given diff. eq. is not exact.

Equation reducible to exact form-

1. If M dx + N dy = 0 be an homogenous equation in x and y, then 1/ (Mx + Ny) is an integrating factor.

Example: Solve-

Sol.

We can write the given equation as-

Here,

M =

Multiply equation (1) by we get-

This is an exact differential equation-

2. I.F. for an equation of the type

IF the equation Mdx + Ndy = 0 be this form, then 1/(Mx – Ny) is an integrating factor.

Example: Solve-

Sol.

Here we have-
 

Now divide by xy, we get-

Multiply (1) by , we get-

Which is an exact differential equation-

3. In the equation M dx + N dy = 0,

(i) If be a function of x only = f(x), then is an integrating factor.

(ii) If be a function of y only = F(x), then is an integrating factor.

Example: Solve-

Sol.

Here given,

M = 2y and N = 2x log x - xy

Then-

Here,

Then,

Now multiplying equation (1) by 1/x, we get-

4. For the following type of equation-

An I.F. is

Where-

Example: Solve-

Sol.

We can write the equation as below-

Now comparing with-

We get-

a = b = 1, m = n = 1, a’ = b’ = 2, m’ = 2, n’ = -1

I.F. =

Where-

On solving we get-

h = k = -3

Multiply the equation by , we get-

It is an exact equation.

So that the solution is-

1. An exact differential equation is formed by differentiating its solution directly without any other process,

Is called an exact differential equation if it satisfies the following condition-

2. If M dx + N dy = 0 be an homogenous equation in x and y, then 1/ (Mx + Ny) is an integrating factor.

3. I.F. for an equation of the type

IF the equation Mdx + Ndy = 0 be this form, then 1/(Mx – Ny) is an integrating factor.

4. For the following type of equation-

An I.F. is

Where-

Equation solvable for p-

Example- Solve-

Sol. Here we have-

or

On integrating, we get-

Equation solvable for y-

Steps-

First- differentiate the given equation w.r.t. x.

Second- Eliminate p from the given equation, then the eliminant is the required solution.

Example: Solve

Sol.

Here we have-

Now differentiate it with respect to x, we get-

Or

This is the Leibnitz’s linear equation in x and p, here

Then the solution of (2) is-

Or

Or

Put this value of x in (1), we get

Equation solvable for x-

Example: Solve-

Sol. Here we have-

On solving for x, it becomes-

Differentiating w.r.t. y, we get-

or

On solving it becomes

Which gives-

Or

On integrating

Thus eliminating from the given equation and (1), we get

Which is the required solution.

Clairaut’s equation-

An equation

y = px + f(p) ...... (2)

is known as Clairaut’s equation.

Differentiating (1) w.r.t. x, we get-

Put the value of p in (1) we get-

y = ax + f(a)

Which is the required solution.

Example: Solve-

Sol.

Put

So that-

Then the given equation becomes-

Or

Or

Which is the Clairaut’s form.

Its solution is-

i.e.

The standard form of of linear differential equation of second order with variable coefficients is-

Here P(x), Q(x) and F(x) are called functions of x and P, Q are known as coefficient of the Differential equation.

Note- The above differential equation will be called non-homogeneous if F(x) is non zero.

Second order DE with constant coefficient (Homogeneous)- The standard form  of second order DE with constant coefficient is-

Here a and b are the constants.

The auxiliary equation or characteristic equation is-

Now the general solution of homogeneous DE depends on the nature of two roots we get from auxiliary equation-

Situation-1: When two roots are distinct and real-

The general solution will be-

Where are any two arbitrary constants.

Situation-2: When two roots are repeated-

The general solution will be-

Situation-3: In case of complex conjugate roots-

Example: Solve- y’’ – 3y’ + 2y = 0, y(0) = -1, y’(0) = 0.

Sol.

Here auxiliary equation will be-

We get-

Here, m = 2, 1 are two real and distinct roots-

Then general solution will be-

Particular solution using conditions y(0)  = -1, we get-

Now using y’(0) = 0, in the derivative of general solution, we get-

Now solving equation (1) and (2)-

Therefore the particular solution will be-

Example: Solve- y’’+3y’+2.25y = 0.

Sol.

We get auxiliary equation as-

Here the roots are repeated.

So that the general solution will be-

Example: Solve- y’’-2y’+5y = 0, y(0) = -3, y’(0) = 1.

Sol.

Here the auxiliary equation will be-

So that-

We get complex conjugate here-

The general solution in this case will be-

Now using y(0) = -3 in general solution, we get-

Now differentiate GS with respect to x-

Using- y’(0) = 1, we get-

Particular solution is-

1. The standard form of of linear differential equation of second order with variable coefficients is-

Here P(x), Q(x) and F(x) are called functions of x and P, Q are known as coefficient of the Differential equation.

2.     The standard form  of second order DE with constant coefficient is-

Here a and b are the constants.

3.     The auxiliary equation -

4.     When two roots are distinct and real-
 

5.     When two roots are repeated-

6.     In case of complex conjugate roots-
 

Method of variation of parameters-

Consider a second order LDE with constant co-efficients given by

Then let the complimentary function is given by

Then the particular integral is

Where u and v are unknown and to be calculated using the formula

u=

Example-1: Solve the following DE by using variation of parameters-

Sol. We can write the given equation in symbolic form as-

To find CF-

It’s A.E. is

So that CF is-     

To find PI-

Here

Now

Thus PI = 

            = 

            = 

             = 

             = 

So that the complete solution is-

Example-2: Solve the following by using the method of variation of parameters.

Sol. This can be written as-

C.F.-

Auxiliary equation is-

So that the C.F. will be-

P.I.-

Here

Now

Thus PI = 

            = 

            = 

So that the complete solution is-

1. The complimentary function -
2. The particular integral is -
3. u=

An equation of the form

Here X is the function of x, is called Cauchy’s homogeneous linear equation.

Example-1: Solve

Sol. As it is a Cauchy’s homogeneous linear equation.

Put

Then the equation becomes [D(D-1)-D+1]y = t   or

Auxiliary equation-

So that-

   C.F.=

Hence the solution is- , we get-

Example-2: Solve

Sol. On putting so that,

and

The given equation becomes-

Or it can be written as-

So that the auxiliary equation is-

C.F. =

Particular integral-

Where

It’s a Leibnitz’s linear equation having I.F.=

Its solution will be-

P.I. =

       =

So that the complete solution is-

An equation of the form-

Is called Legendre’s linear equation.

Example-3: Solve

Sol. As we see that this is a Legendre’s linear equation.

Now put

So that-

And

Then the equation becomes- D (D – 1)y+ Dy + y = 2 sin t

Its auxiliary equation is-

And particular integral-

               P.I. =

Note -

Hence the solution is -

1. Cauchy’s homogeneous linear equation-
    

We know that the solution of the differential equation-

Are

These are the power series solutions of the given differential equations.

Ordinary Point-

Let us consider the equation-

Here are polynomial in x.

X = a is an ordinary point of the above equation if does not vanish for x = a.

Note- If vanishes for x = a, then  x =  a is a singular point.

Solution of the differential equation when x = 0 is an ordinary point, which means does not vanish for x = 0.

1. Let be the solution of the given differential equation.

2. Find

3.

4. Substitute the expressions of y, etc. in the given differential equations.

5. Calculate Coefficients of various powers of x by equating the coefficient to zero.

6. Put the values of In the differential equation to get the required series solution.

Example- Solve

Sol.

Here we have-

Let the solution of the given differential equation be-

Since x = 0 is the ordinary point of the given equation-

Put these values in the given differential equation-

Equating the coefficients of various powers of x to zero, we get-

Therefore the solution is-

Example: Solve in series the equation-

Sol.

Here we have-

Let us suppose-

Since x = 0 is the ordinary point of (1)-

Then-

And

Put these values in equation (1)-

We get-

Equating to zero the coefficients of the various powers of x, we get-

And so on….

In general we can write-

Now putting n = 5,

Put n = 6-

Put n = 7,

Put n = 8,

Put n = 9,

Put n = 10,

Put the above values in equation (1), we get-

Frobenius method-

This method is also called generalized power series method.

If x = 0 is a regular singularity of the equation.

……..(1)

Then the series solution is-

Which is called Frobenius series.

On equating the coefficient of lowest power of x in the identity to zero, we get a quadratic equation in ‘m’.

We will get two values of m. The series solution of (1) will depend on the nature of the roots of the indicial equation-

Case-1: when roots m1 and m2 are distinct and these are not differing by an integer-

The complete solution in this case will be-

Case-2: when roots m1 and m2 are equal-

Case-3: when roots are distinct but differ by an integer-

Case-4: Roots are distinct and differing by an integer, making some coefficient indeterminate-

Example: Find solution in generalized series form about x = 0 of the differential equation

Sol.

Here we have

………… (1)

Since x = 0 is a regular singular point, we assume the solution in the form

So that

Substituting for y, in equation (1), we get-

…..(2)

The coefficient of the lowest degree term in (2) is obtained by putting k

= 0 in first summation only and equating it to zero. Then the indicial equation is

Since

The coefficient of next lowest degree termin (2) is obtained by putting

k = 1 in first summation and k = 0 in the second summation and equating it to zero.

Equating to zero the coefficient of the recurrence relation is given by

Or

Which gives-

Hence for-

Form m = 1/3-

Hence for m = 1/3, the second solution will be-

The complete solution will be-

1. Frobenius method-

If x = 0 is a regular singularity of the equation.

Then the series solution is-

2.     when roots m1 and m2 are distinct and these are not differing by an integer-

3.     when roots m1 and m2 are equal-

4.     when roots are distinct but differ by an integer-

5.     Roots are distinct and differing by an integer, making some coefficient indeterminate-