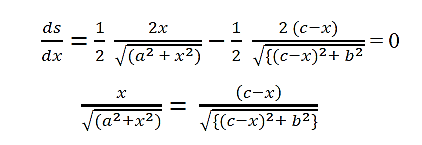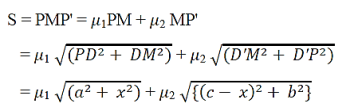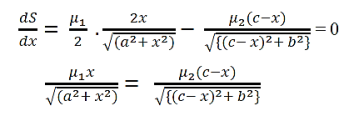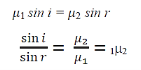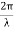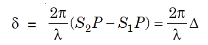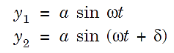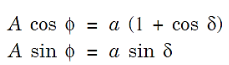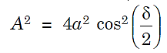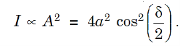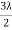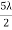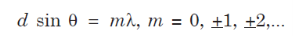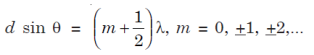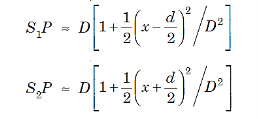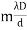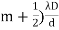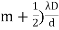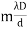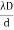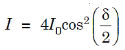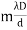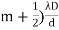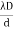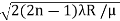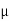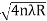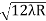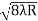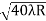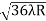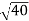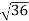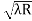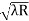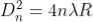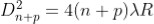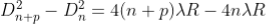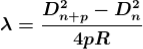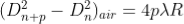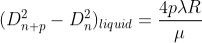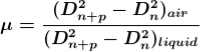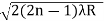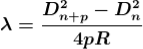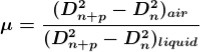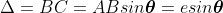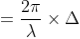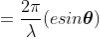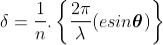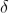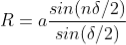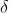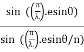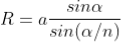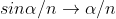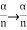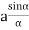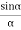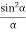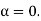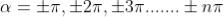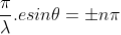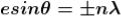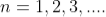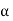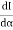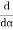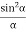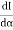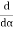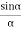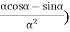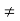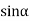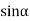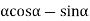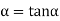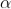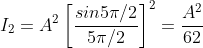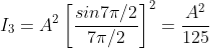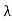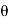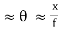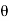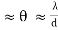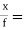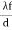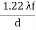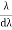UNIT-2
PROPAGATION OF LIGHT AND GEOMETRIC OPTICS
2.1.1 FERMAT’S PRINCIPLE
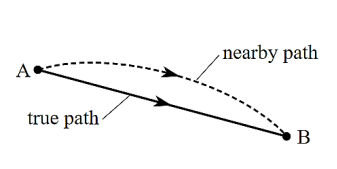
In 1658 Pierre De Fermat, a French mathematician enunciated the principle of least time. When light travels between two fixed points it does so in such a way that its path has the shortest possible length. If correct, this rule can certainly explain rectilinear propagation; it would simply be a consequence of the geometrical fact that given any two points A and B (see Figure), a straight line provides the shortest path between them.
Figure 1: A light ray follows the shortest route between two fixed points. Any nearby path is longer. |
A ray of light in passing from one point to another through a set of media by any number of reflections or refractions chooses a path along which the time taken is minimum or the least.
Based on this principle, the laws of rectilinear propagation, the laws of reflection and refraction can be derived. However in some cases, it has been found that the time taken by light is not minimum but maximum or else it is neither maximum nor minimum but it is stationary. This is found in case of image formation by lenses, in which all rays starting from an object point, reaching to the image point; choose the path of maximum or minimum time. Therefore, the modified form of Fermat's principle of least time is known as Fermat's principle of stationary time or Fermat's principle of extreme path, which may be stated as follows:
A ray of light in passing from one point to another through a set of media by any number of reflections or refractions chooses a path for which the time taken is either minimum or maximum or stationary.
2.1.2 MIRAGE EFFECT
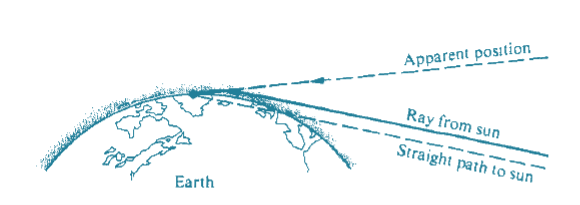
When light rays from the Sun pass through the inhomogeneous atmosphere of the Earth, as shown in Figure 2, they bend so as to traverse the lower, denser regions as abruptly as
|
Figure 2: The bending of rays through inhomogeneous media. Because the rays bend as they pass through the atmosphere the Sun appears higher in the sky.
According to Fermat's Principle, a ray leaving a branch in Figure heading somewhat downward would take a route that minimized the optical path length (OPL). Such a ray would bend upward, passing through more of the less dense air than if it had travelled straight.
To appreciate how that works, imagine the air divided into an infinite number of infinitesimally thin constant-n horizontal layers. A ray passing from layer to layer would bend (via Snell's Law) slightly upward at each interface
Of course, if the ray comes down nearly vertically it makes a small angle-of-incidence at each interface between layers, only bends slightly, and soon strikes the ground where no one will "see" it.
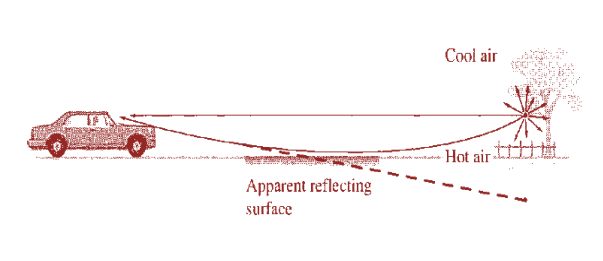
Figure 3: At very low angles the rays appear to be coming from Beneath the road as if reflected in a puddle. |
On the other hand, it is possible that a light ray that comes in at a shallow enough angle to begin with could ultimately approach an interface at glancing incidence. It would then be completely reflected, thereby starting its climb back up into the denser air.
Any viewer, off on the left who receives these bent rays, naturally projects them straight backward as if they were reflected from a mirrored surface. Depending on where you stand, you'll see a different mirage puddle, but it will always be far from you and so will always disappear as you approach it. The effect is particularly easy to view on long modem highways. The only requirement is that you look at the road at near glancing incidence, because the rays bend very gradually.
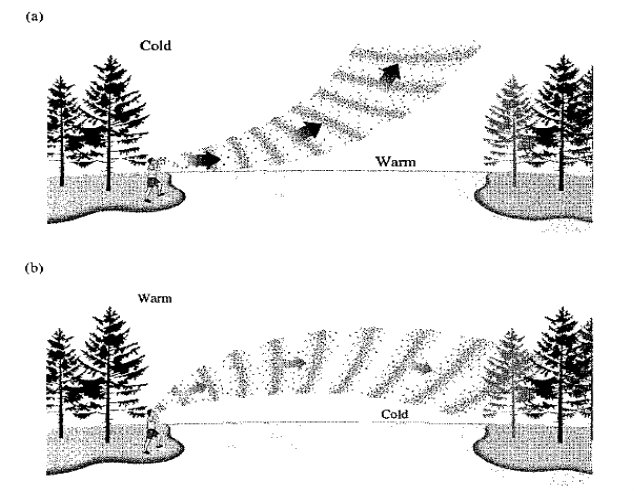
The same effect is well known as it applies to sound. Figure 4 depicts the alternative understanding in terms of waves. The wave fronts bend because of temperature-induced changes in speed and therefore in wavelength. (The speed of sound is proportional to the square root of the temperature.) The noises of people on a hot beach climb up and away, and the place can seem strangely quiet. The opposite occurs in the evening when the ground cools before the upper air and distant sounds can clearly be heard.
Figure 4 : (a) when the surface air is cold, (b) when it's warm
|
The puddle mirage can be understood via waves; the speed, and therefore the wavelength, increase in the less dense medium. That bends the wavefronts and the rays. The same effect is common with sound waves; (a) when the surface air is cold, sounds can be heard much farther than normal. (b) And when it's warm, sounds seem to vanish into the air.
On the basis of Fermat's principle, you can derive laws of reflection and refraction
2.1.3 LAWS OF REFLECTION
When light ray falls on a smooth polished surface separating two media, it comes back in the same medium, the phenomenon is called reflection and the boundary is called reflecting surface. The light obeys following two laws of reflection.
First law
The incident ray, reflected ray and the normal to the surface at the point of incidence all lie in one plane.
Prove
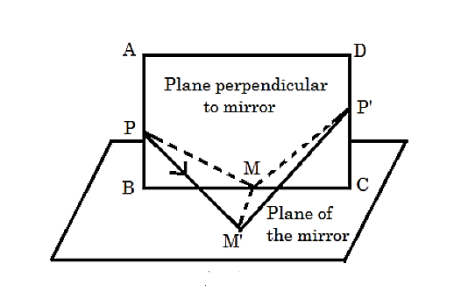
Let the plane ABCD be normal to the plane mirror shown in figure 5. P is point object imaged by mirror as P. Consider a point M' on the plane mirror, but not on plane ABCD. Let a ray PM' be reflected as MP'. Draw a normal M'M on plane ABCD. Point M is the foot of the normal on ABCD.
Now PMM' and P'MM' are right angle triangles. PM' and P'M' are respective hypotenuse. Therefore, we have
PM' > PM and P'M' > P'M
But Fermat's principle demands that the path followed must be the shortest, i.e., the light would not travel along PM'P'. As we shift M' towards M the path of light ray becomes shorter. It is seen that the shortest possible path is PMP', where the point of incidence M lies on plane ABCD. PM and MP' are the reflected rays. This proves the first law of reflection.
Figure 5: Laws of reflection (First law)
|
Second law
For a smooth surface, the angle of incidence is equal to the angle of reflection.
Prove
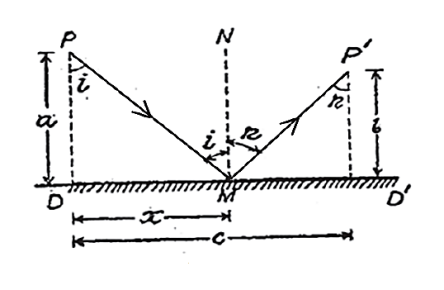
Assuming DD' is a reflecting plane shown in figure. Object P is imaged as P' and M is the point of incident. The normal to the plane at this point is MN and is shown by dotted line.
Figure 6: Laws of reflection (Second law) |
PM and MP' are the incidence and reflected rays.
Let I and r are the angles of incidence and reflection respectively. Let us suppose distances PD= a, P'D' = b, DM = x, DD' = c. The ray of light travels in air from P to P'. Let the path PMP' be s, then the total distance covered by light ray be s = P MP' = PM + MP' = (PD2+ DM2) + (D'M2 + D' P'2) = {(a2 + x2)} + {(c — x)2 +b2} |
It is evident that the path from P to P' remains the same even if the point of incidence M shifts. Shifting of M changes x only. According to Fermat's principle the path PMP' must be either minimum or maximum. It means that the differential coefficient of s with respect to x must be zero, i.e.
We have,
|
From figure we have
|
Hence you can see that the second law of reflection is derived from Fermat's principle. Further the second differential co-efficient of s, i.e., d2s/dx2 comes out to be positive, which proves that the path is minimum (or path of least time).
2.1.4 LAWS OF REFRACTION
When a ray of light passes from one homogenous medium to another, the phenomenon of bending of light ray towards or away from the nonnal is called refraction. Again there are following two laws of refraction.
Figure 7: Laws of refraction (First law) |
First Law:
The incident ray, refracted ray and the normal at the point of incidence all lie in one plane.
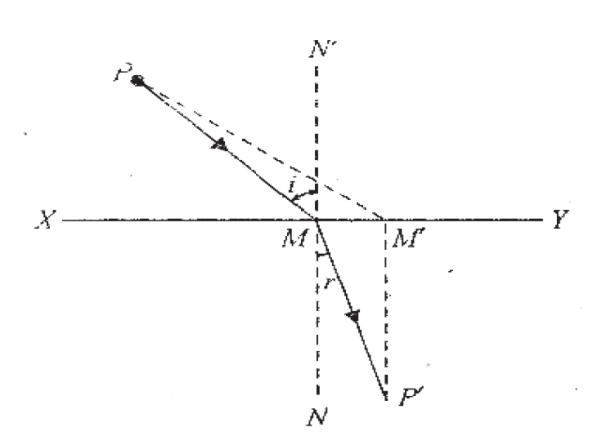
Let us assume XY be a plane surface dividing two media shown in figure 7. A ray starting from point P is incident on M. It is refracted as MP' in the other medium, ∠i and ∠r are the angles of incidence and refraction. Let us assume that the ray follows path PM'P' instead of PMP'. It is evident that
PM’ + M'P' > PM + MP'
Therefore, path PM'P' is not possible. If you shift M’ towards M, the path from P to P' through M shortens. It is shortest when M' is coincident with M which is in accordance with Fermat's principle and proves the first law.
Second Law:
The ratio of the sine of angle of incidence to the sine of angle of refraction is a constant for a given pair of media.
You can further prove that the ratio of the sin i to sin r is equal to the refractive index of second medium with respect to the first medium which is also known as Snell's law.
Figure 8: Laws of refraction (Second law) |
In figure XY is a plane surface dividing two media of refractive indices μ1 and μ2. Consider a point object P in the first medium, PM and MP’ are the incident and refracted rays, i and r are the angle of incidence and refraction.
PD=a, DM=x, DD’=c, D’P’ =b
If a ray of light travels a distance S in a medium of refractive index μ, than product μ.S is called the optical path in the medium.
The optical path from P to P' is given by
|
Now, for S to be minimum dS/dx must be zero and d2S/dx2 positive. Differentiating S with respect to x, we get
Or
|
Using triangles PMD and PMD', you can write the above relation as
|
Where 1μ2 is the refractive index of the second medium with respect to the first medium. This is the Snell's law of refraction
You can show that the second differential coefficient of S. i.e., d2S/dx2 for the plane suffice comes out to be positive. It proves that the second law of refraction is in accordance with Fermat's principle, i.e., the actual path is minimum or path of least time. But you will see that, this condition is satisfied in the case of plane surfaces only and not in the case of curved surfaces. For curved surfaces, the path may be a maximum or minimum
Key Takeaways
- In 1658 Pierre De Fermat, a French mathematician enunciated the principle of least time. When light travels between two fixed points it does so in such a way that its path has the shortest possible length.
- This rule can certainly explain rectilinear propagation.
- According to Fermat's Principle, a ray leaving a branch in Figure heading somewhat downward would take a route that minimized the optical path length (OPL). Such a ray would bend upward, passing through more of the less dense air than if it had travelled straight.
- When light ray falls on a smooth polished surface separating two media, it comes back in the same medium, the phenomenon is called reflection and the boundary is called reflecting surface.
- When a ray of light passes from one homogenous medium to another, the phenomenon of bending of light ray towards or away from the nonnal is called refraction.
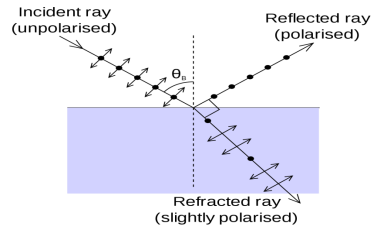
The Brewster’s law can be used to polarise the light by reflection. When unpolarised light is incident on the boundary between two transparent media, the reflected light is polarised with its electric vector perpendicular to the plane of incidence when the refracted and reflected rays make a right angle with each other.
Thus we have seen that when reflected wave is perpendicular to the refracted wave, the reflected wave is a totally polarised wave. The electric field vectors of all unpolarized light may be resolved into two components as follows;
- Tangential component- in the plane of incidence.
- Normal components – in the plane perpendicular to plane of incidence.
The angle of incidence in this case is called Brewster’s angle
Figure 9: Brewster’s Angle |
If the angle of incidence θi is varied, the reflected coefficient ‘r’ for the em waves corresponding to the tangential component will vary as shown in figure. As θi increases r will decrease.
At θi = Brewster angle (about 57° for glass) r will be zero and no reflection of the tangential component will take place.
The reflected beam will contain light waves having only the normal component for the electric field as shown in figure that is the reflected light will be plane polarized with the oscillations of electric field vector normal to the plane of incidence.
The em waves are generated because of the oscillation of electric charge. The electric field vectors of the transmitted ray act on the electrons in the dielectric.
Since the intensity of em wave emitted by the oscillating charge is maximum in a direction normal to the plane of oscillation, and zero along the line of oscillations for the plane polarized light having electric field vector in the plane of incidence, there will be no emition of em waves in a direction normal to the reflected ray. In figre the direction along which no emission should accur is called as zero intensity line. Let the angle between the reflected ray and the zero intensity line be 𝛿 the angle between the reflected and tranmitted ray is π/2 + 𝛿 suppose we arrange the angle of incidence such that
n=sinθi / sinθr n=sinθi / sin(π/2 – θi) n=sinθi / cosθi n=tan θi that is possible when θi + θr = π/2 according to Brewster’s law from figure θi + θr+ π/2 + = π As θi + θr = π/2 So π/2+ π/2 + = π = 0 |
The line of zero intensity and the refected ray will coincide. Thuse there will be no reflection of light when the angle of incidence is equal to Brewster’s angle.
Thus the unpolarized light can be polarized by reflection as the reflected beam will contain light waves having electric field vector oscilating along normal to the plane of the incidence only.
Key takeaways
- The Brewster’s law can be used to polarise the light by reflection.
- The electric field vectors of all unpolarized light may be resolved into two components
- The angle of incidence in this case is called Brewster’s angle
- If the angle of incidence θi is varied, the reflected coefficient ‘r’ for the em waves corresponding to the tangential component will vary
- At θi = Brewster angle (about 57° for glass) r will be zero and no reflection of the tangential component will take place.
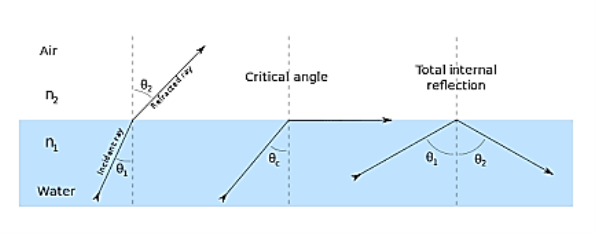
Total internal reflection:
When the light ray travels from denser medium to rarer medium the refracted ray bends away from the normal. When the angle of incidence is greater than the critical angle, the refracted ray again reflects into the same medium. This phenomenon is called total internal reflection. The refracted ray bends towards the normal as the ray travels from rarer medium to denser medium. The refracted ray bends away from the normal as it travels from denser medium to rarer medium.
Figure 10 – Total Internal Reflection |
When light passes from a medium with one index of refraction (m1), to another medium with a lower index of refraction (m2), it bends or refracts away from an imaginary line perpendicular to the surface (normal line). As the angle of the beam through m1 becomes greater with respect to the normal line, the refracted light through m2 bends further away from the line.
At one particular angle (critical angle), the refracted light will not go into m2, but instead will travel along the surface between the two media (sine [critical angle] = n2/n1 where n1 and n2 are the indices of refraction [n1 is greater than n2]). If the beam through m1 is greater than the critical angle, then the refracted beam will be reflected entirely back into m1 (total internal reflection), even though m2 may be transparent.
In physics, the critical angle is described with respect to the normal line. In fiber optics, the critical angle is described with respect to the parallel axis running down the middle of the fiber. Therefore, the fiber-optic critical angle = (90 degrees - physics critical angle).
In an optical fiber, the light travels through the core (m1, high index of refraction) by constantly reflecting from the cladding (m2, lower index of refraction) because the angle of the light is always greater than the critical angle. Light reflects from the cladding no matter what angle the fiber itself gets bent at, even if it's a full circle.
Because the cladding does not absorb any light from the core, the light wave can travel great distances. However, some of the light signal degrades within the fiber, mostly due to impurities in the glass. The extent that the signal degrades depends upon the purity of the glass and the wavelength of the transmitted light
When the angle of incidence (θ1) is progressively increased, there will be progressive increase of refractive angle (θ2). At some condition (θ1) the refractive angle (θ2) becomes 90o to the normal. When this happens the refracted light ray travels along the interface. The angle of incidence (θ1) at the point at which the refractive angle (θ1) becomes 90 degree is called the critical angle.
It is denoted by θc. The critical angle is defined as the minimum angle of incidence (θ1) at which the ray strikes the interface of two media and causes an angle of refraction (θ2) equal to 90o. Figure 10 shows critical angle refraction
Hence at critical angle θ1= θc and θ2= 90o . Using Snell‘s law: n1 sin θ1 = n2 sin θ2 n1 sin θc = n2 sin90o sin θc = n2 / n1 θc = sin-1 (n2 / n1) |
The actual value of critical angle is dependent upon combination of materials present on each side of boundary. Optical Fibre works on the principle of Total Internal Reflection.
Key takeaways
- When the light ray travels from denser medium to rarer medium the refracted ray bends away from the normal. When the angle of incidence is greater than the critical angle, the refracted ray again reflects into the same medium. This phenomenon is called total internal reflection.
- The critical angle is defined as the minimum angle of incidence (θ1) at which the ray strikes the interface of two media and causes an angle of refraction (θ2) equal to 90o.
- The actual value of critical angle is dependent upon combination of materials present on each side of boundary.
- Optical Fibre works on the principle of Total Internal Reflection.
Huygens' Principle
In 1678 Huygens proposed a model where each point on a wavefront may be regarded as a source of waves expanding from that point.
Every point on a wavefront is a source of wavelets that spread out in the forward direction at the same speed as the wave itself. The new wavefront is a line tangent to all of the wavelets.
So Huygens’s Principle states that every point on a wavefront is a source of wavelets, which spread forward at the same speed.
|
Figure 11: Huygens' Principle
The expanding waves may be demonstrated in a ripple tank by sending plane waves toward a barrier with a small opening. If waves approaching a beach strike a barrier with a small opening, the waves may be seen to expand from the opening.
Huygens-Fresnel Theory:
According to Huygens’s wave theory of light, each progressive wave produces secondary waves, the envelope of which forms the secondary wave front.
In figure 12 (a). S is a source of monochromatic light and MN is a small aperture. XY is the screen placed in the path of light. AB is the illuminated portion of the screen and above A and below B is the region of the geometrical shadow. Considering MN as the primary wave front. According to Huygens’s construction, if secondary wave fronts are drawn, one would expect encroachment of light in the geometrical shadow. Thus, the shadows formed by small obstacles are not sharp. This bending of light round the edges of an obstacle or the encroachment of light within the geometrical shadow is known as diffraction. Similarly, if an opaque obstacle MN is placed in the path of light [Figure 12 (b)], there should be illumination in the geometrical shadow region AB also. But the illumination in the geometrical shadow of an obstacle is not commonly observed because the light sources are not point sources and secondly the obstacles used are of very large size compared to the wavelength of light. If a shadow of an obstacle is cast by an extended source, say a frosted electric bulb, light from every point on the surface of the bulb forms its own diffraction pattern (bright and dark diffraction bands) and these overlaps such that no single pattern can be identified. The term diffraction is referred to such problems in which one considers the resultant effect produced by a limited portion of a wave front.
Figure 12: Huygens’s wave theory of light, |
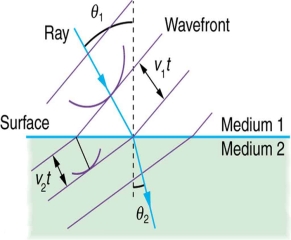
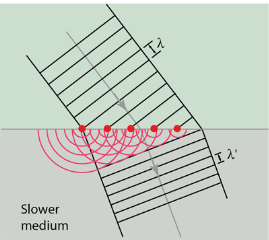
Huygens' principle provides a convenient way to visualize refraction. If points on the wavefront at the boundary of a different medium serve as sources for the propagating light, one can see why the direction of the light propagation changes.
The law of refraction can be explained by applying Huygens’s principle to a wavefront passing from one medium to another (see Figure 13). Each wavelet in the figure was emitted when the wavefront crossed the interface between the media. Since the speed of light is smaller in the second medium, the waves do not travel as far in a given time, and the new wavefront changes direction as shown. This explains why a ray changes direction to become closer to the perpendicular when light slows down.
Figure 13: Law of refraction by Huygens’s principle |
If we pass light through smaller openings, often called slits, we can use Huygens’s principle to see that light bends as sound does. The bending of a wave around the edges of an opening or an obstacle is called diffraction.
Diffraction is a wave characteristic and occurs for all types of waves. If diffraction is observed for some phenomenon, it is evidence that the phenomenon is a wave. Thus the horizontal diffraction of the laser beam after it passes through slits is evidence that light is a wave.
Diffraction phenomena are part of our common experience. The luminous border that surrounds the profile of a mountain just before the sun rises behind it, the light streaks that one sees while looking at a strong source of light with half shut eyes and the coloured spectra (arranged in the form of a cross) that one sees while viewing a distant source of light through a fine piece of cloth are all examples of diffraction effects. Augustine Jean Fresnel in 1815, combined in a striking manner Huygens’ wavelet with the principle of interference and could satisfactorily explain the bending of light round obstacles and also the rectilinear propagation of light.
Key takeaways
- Huygens’s Principle states that every point on a wavefront is a source of wavelets, which spread forward at the same speed.
- According to Huygens’s wave theory of light, each progressive wave produces secondary waves, the envelope of which forms the secondary wave front.
- Huygens' principle provides a convenient way to visualize refraction.
- Huygens’s principle to see that light bends as sound does. The bending of a wave around the edges of an opening or an obstacle is called diffraction.
The principle of superposition says:
When two or more waves cross at a point, the displacement at that point is equal to the sum of the displacements of the individual waves.
The individual wave displacements may be positive or negative. If the displacements are vectors, then the sum is calculated by vector addition.
Figure 14: Principle of superposition |
Superposition is an important idea that can explain phenomena including interference, diffraction and standing waves. It works for any type of wave (sound waves, water surface waves, electromagnetic waves...) but only works under certain conditions, which we describe below.
When the waves pass beyond a point of intersection, they separate out again and are unaffected.
The principle of superposition can be applied to any type of wave providing that:
- The waves being superposed are of the same type (e.g., all are electromagnetic waves)
- The medium that the waves are propagating through behaves linearly, i.e., when part of the medium has twice the displacement then it has twice the restoring force. This is usually true when the amplitudes are relatively small. For example, for waves on water, it is a good approximation for small ripples on a pond whose amplitude is much smaller than their wavelength.
If the waves are also coherent - i.e., if they all have the same frequency and a constant phase difference - then the superposition resembles another wave with the same frequency.
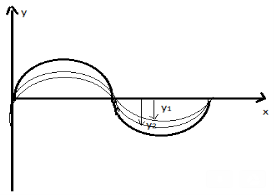
Considering two waves, travelling simultaneously along the same stretched string in opposite directions as shown in the figure above. We can see images of waveforms in the string at each instant of time. It is observed that the net displacement of any element of the string at a given time is the algebraic sum of the displacements due to each wave.
Let us say two waves are travelling alone and the displacements of any element of these two waves can be represented by y1(x, t) and y2(x, t). When these two waves overlap, the resultant displacement can be given as y(x,t).
Mathematically, y (x, t) = y1(x, t) + y2(x, t) As per the principle of superposition, we can add the overlapped waves algebraically to produce a resultant wave. Let us say the wave functions of the moving waves are y1 = f1(x–vt), y2 = f2(x–vt) ………. yn = fn (x–vt) then the wave function describing the disturbance in the medium can be described as y = f1(x – vt)+ f2(x – vt)+ …+ fn(x – vt) or, y= Let us consider a wave travelling along a stretched string given by, y1(x,t) = A sin (kx – ωt) and another wave, shifted from the first by a phase φ, given as y2(x, t) = A sin (kx – ωt + ϕ) From the equations we can see that both the waves have the same angular frequency, same angular wave number k, hence the same wavelength and the same amplitude A. Now, applying the superposition principle, the resultant wave is the algebraic sum of the two constituent waves and has displacement y(x, t) = A sin (kx – ωt) + A sin (kx – ωt + ϕ) As, sin A + sin B = 2sin (A+B)/2 .cos (A−B)/2 The above equation can be written as, y(x, t) = [2A cos ϕ /2 ] sin (kx − ωt + ϕ /2) The resultant wave is a sinusoidal wave, travelling in the positive X direction, where the phase angle is half of the phase difference of the individual waves and the amplitude as [2cos ϕ /2] times the amplitudes of the original waves. Hence, the superposition of waves can lead to the following three effects:
|
THEORY OF INTERFERENCE FRINGES
INTERFERENCE
Interference in light waves occurs whenever two or more waves overlap at a given point.
TYPES OF INTERFERENCE
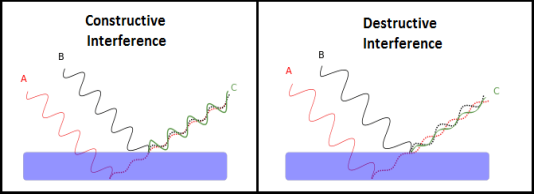
Interference of light waves can be either constructive interference or destructive interference.
- Constructive Interference: Constructive interference takes place when the crest of one wave falls on the crest of another wave such that the amplitude is maximum. These waves will have the same displacement and are in the same phase.
- Destructive Interference: In destructive interference the crest of one wave falls on the trough of another wave such that the amplitude is minimum. The displacement and phase of these waves are not the same.
Figure 15: Types of interference
|
We know that the superposition of two mechanical waves can be constructive or destructive. In constructive interference, the amplitude of the resultant wave at a given position or time is greater than that of either individual wave, whereas in destructive interference, the resultant amplitude is less than that of either individual wave.
Light waves also interfere with each other. Fundamentally, all interference associated with light waves arises when the electromagnetic fields that constitute the individual waves combine.
If two light bulbs are placed side by side, no interference effects are observed because the light waves from one bulb are emitted independently of those from the other bulb. The emissions from the two light bulbs do not maintain a constant phase relationship with each other over time. Light waves from an ordinary source such as a light bulb undergo random phase changes in time intervals less than a nanosecond.
Therefore, the conditions for constructive interference, destructive interference, or some intermediate state are maintained only for such short time intervals. Because the eye cannot follow such rapid changes, no interference effects are observed. Such light sources are said to be incoherent.
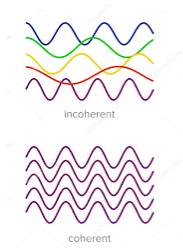
Two sources are said to be coherent when the waves emitted from them have the same frequency and constant phase difference.
Interference from such waves happen all the time, the randomly phased light waves constantly produce bright and dark fringes at every point. But, we cannot see them since they occur randomly. A point that has a dark fringe at one moment may have a bright fringe at the next moment. This cancels out the effect of the interference effect, and we see only an average brightness value. The interference is not said to be sustained since we cannot observe it.
Definition: A predictable correlation of the amplitude and phase at any one point with other point is called coherence.
Figure 16: Incoherence and coherence
|
COHERENT SOURCES
Two waves are said to be coherent, the waves must have
In case of convectional light, the property of coherence exhibits between a source and its virtual source where as in case of laser the property coherence exists between any two of more light waves.
There are two types of coherence
i) Temporal coherence
ii) Spatial coherence
TEMPORAL COHERENCE (OR LONGITUDINAL COHERENCE):-
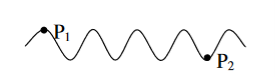
The predictable correlation of amplitude and phase at one point on the wave train w .r. t another point on the same wave train, then the wave is said to be temporal coherence
To understand this, let us consider two points P1 and P2 on the same wave train, which is continuous as in shown in figure.
Figure 17: Wave train
|
Suppose the phase and amplitude at any one point is known, then we can easily calculate the amplitude and phase for any other point on the same wave train by using the wave equation
y= a sin ( Where ‘a’ is the amplitude of the wave and ‘x’ is the displacement of the wave at any instant of time‘t’. |
SPATIAL COHERENCE (OR TRANSVERSE COHERENCE)
The predictable correlation of amplitude and phase at one point on the wave train w. r .t another point on a second wave, then the waves are said to be spatial coherence (or transverse coherence)
Figure 18: Spatial coherence
|
CONDITIONS FOR SUSTAINED INTERFERENCE
In a sustained interference pattern, the position of maximum and minimum intensity regions remains constant with time. To obtain the sustained interference, the following conditions are required:
- The sources must be coherent, that is, they must maintain a constant phase with respect to each other.
- The two light sources must emit continuous waves of the same wavelength and having the same time period.
- The distance between the two sources of light must be small. This gives large fringe width so that the fringes are separately visible.
- The sources should be monochromatic, that is, of a single wavelength.
- The two light sources must emit waves in nearly the same direction.
- Light source must be a point source.
- The distance between the two sources and screen must be large. This gives again large fringe width so that the fringes are separately visible.
The phenomenon of interference may be grouped into two categories:
- Division of Wavefront
- Division of Amplitude
Division of Wavefront
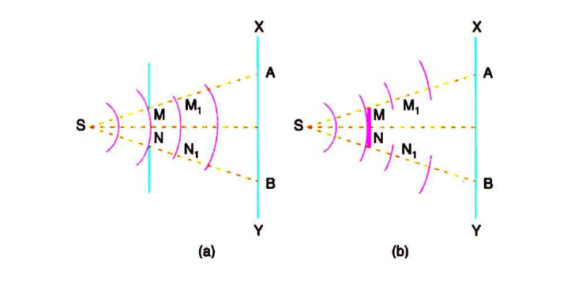
Under this category, the coherent sources are obtained by dividing the wavefront, originating from a common source, by employing mirrors, biprisms or lenses. This class of interference requires essentially a point source or a narrow slit source. The instruments used to obtain interference by division of wavefront are the Fresnel biprism, Fresnel mirrors, Lloyd's mirror, lasers, etc.
Some of the standard arrangements used to observe two-wave interference by division of the wavefront are shown in Figure.
Figure 19: Two-wave interference; (a) Young’s two-slit arrangement, (b) Fresnel’s biprism, (c) Fresnel’s two mirrors, (d) Loyd’s mirror |
In Figure 19(a) The narrow slits S1 and S2 in Young’s double slit arrangement intercept portions of the spherical wavefront and act as real mutually coherent point sources, diffracting light in the forward direction. Interference among the diffracted waves can be observed anywhere in the region of overlap (shaded portion) behind the plane of the slits. Historically, the interference produced in Young’s double slit experiment was not accepted as a conclusive proof of the wave nature of light because it was thought that the fringes in Young’s experiment could arise due to some unexplained interaction of light with the edges of the slits.
In Figure 19(b) Fresnel’s biprisms arrangement, however, established the wave nature of light beyond any doubt. Fresnel’s biprism consists of two small angle (a few degrees) prisms in a manner that the incident spherical wavefront is split by the two prisms. The split wavefronts travel in different directions, eventually overlap and produce interference. S1 and S2 act as virtual but mutually coherent point sources.
Figure 19(c) shows the two-mirror arrangement, also devised by Fresnel. Here, the portions of the spherical wavefront reflected by the two mirrors overlap to produce interference. The source images S1 and S2, formed by the two mirrors, are virtual but mutually coherent.
In Figure 19(d) shows Lloyd’s single mirror arrangement, interference is produced by the portion of the wavefront reflected by the mirror and the portion which propagates directly to the region of superposition. In this case, the point source S and its virtual image S’ act as mutually coherent point sources.
Division of Amplitude
In this method, the amplitude of the incident beam is divided into two or more parts either by partial reflection or refraction. Thus, we have coherent beams produced by division of amplitude. These beams travel different paths and are finally brought together to produce interference. The effects resulting from the superposition of two beams are referred to as two beam interference and those resulting from superposition of more than two beams are referred to as multiple beam interference. The interference in thin films, Newton's rings, and Michelson's interferometer are examples of two beam interference and Fabry-Perot's interferometer is an example of multiple beam interference.
In case of division by wavefront, we considered two-wave interference when different portions of the wavefront are made to propagate in different directions and then recombined. Now, we discuss two-wave interference when a quasi-monochromatic wave is incident on a thin transparent film as shown in Figure. Here we will discuss interference by division of amplitude.
The wave is partly reflected and partly transmitted at each interface. Amplitudes of successively reflected and transmitted waves diminish rapidly for films of low reflectivity. The amplitude transmission coefficient for passage of the wave from the medium of refractive index n1 to the medium of refractive index n2 is t and t’ is the corresponding amplitude transmission coefficient for passage in the reverse direction.
Figure 20: Reflection and transmission across a thin film. |
The amplitude reflection coefficients for the external and internal reflections are r and r’=−r, respectively. For sufficiently small r (r2 <1), only two waves need to be considered in reflection as well as in transmission, leading to two-wave interference. The amplitudes of the first two waves in reflection are comparable, but those in transmission differ considerably.
As a result, interference fringes in reflected light have higher visibility than those in transmitted light.
Key takeaways
- The principle of superposition says that when two or more waves cross at a point, the displacement at that point is equal to the sum of the displacements of the individual waves.
- Interference in light waves occurs whenever two or more waves overlap at a given point.
- Interference of light waves can be either constructive interference or destructive interference.
- A predictable correlation of the amplitude and phase at any one point with other point is called coherence. There are two types of coherence; Temporal coherence and Spatial coherence
- The phenomenon of interference may be grouped into two categories: Division of Wavefront and Division of Amplitude
- The instruments used to obtain interference by division of wavefront are the Fresnel biprism, Fresnel mirrors, Lloyd's mirror, lasers, etc.
- The interference by division of amplitude is seen in thin films, Newton's rings, and Michelson's interferometer (examples of two beam interference) and Fabry-Perot's interferometer (example of multiple beam interference).
In 1801 Thomas performed double slit experiment. He gave evidence for the wave theory of light from double slit interference experiment.
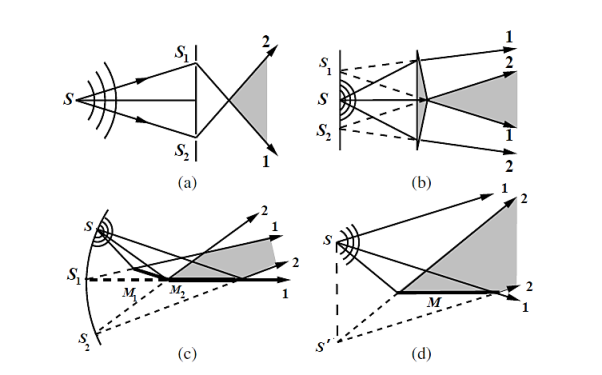
Suppose monochromatic light of wavelength λ is allowed to pass through a slit S and two parallel slits S1 and S2 are placed at equidistant from S.
Figure 21: Young’s double slit experiment |
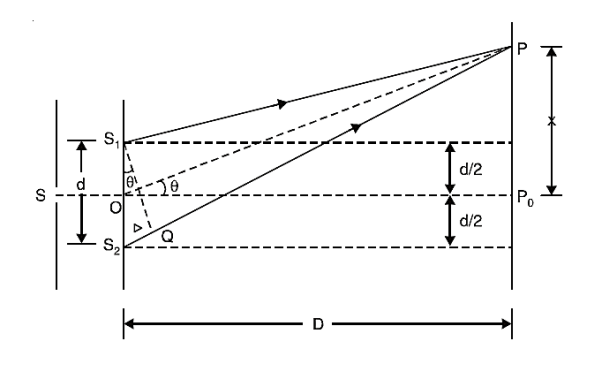
The slits S1 and S2 act as coherent sources. Both these slits are of same width, they will emit waves or disturbances of equal amplitudes. These disturbances are superimposed at P on the screen with a phase difference
where Δ = S2P – S1P is the path difference. Let us consider y1 is the displacement due to the waves coming from S1 and y2 is displacements due to the waves coming from S2, Thus, we have
where a is the amplitude of both the waves. According to the principle of superposition, the resultant displacement y is given by
where
and A is the amplitude of the resultant displacement. Thus,
The intensity I of the light at P is proportional to the square of the resultant amplitude.
Thus, we can write the equation (5) as
where I0 is the intensity on the screen associated with light from one of the two slits, the other slit being temporarily covered. For maximum intensity, δ = 0, 2π, 4π,... or, path difference Δ = 0, λ, 2λ... ; and for minimum intensity δ = π, 3π, 5π,... or, Δ = The point P0 on the screen is equidistant from S1 and S2. At P0, Δ = 0 and δ = 0. We have maximum intensity at P0. From S1 we drop a perpendicular S1Q on S2P and suppose ∠ S2S1Q = θ, then Δ = d sin θ and δ =2π λ d sin θ, where d = S1S2 = separation between the coherent sources. Thus, the conditions for maxima and minima are Maxima
Minima
Suppose the point P is at a distance x from P0 and D is the distance of the screen from the coherent sources. Then
D is the distance between slits and screen which is usually very large compared to d or x. Then, we can write
The path difference Δ becomes
where ∠POP0 = θ and The conditions for bright and dark fringes are Bright fringes x = Dark fringes x =( At P0, m = 0, i.e., zeroth order bright fringe is formed at P0. The distance between any two consecutive bright or dark fringes is known as fringe width and it is given by β =( Thus, alternately dark and bright parallel fringes are formed on both sides of P0. The width of the bright fringe is equal to the width of the dark fringe. The intensity at P is given by Eqn. (6). Since the amplitude a decreases with the increasing distance S1P, the intensity decreases with increasing x, and the intensity decreases with increasing D. The intensity at bright points is 4I0 and at dark point it is zero. Here, the energy is transferred from the points of minimum intensity to the points of maximum intensity. The average value of cos2(δ/2) is 1/2. Therefore, the average intensity of the interference pattern is < I > = 2I0. Now, with two independent sources, each beam acts separately and contributes I0 and so without interference we would have a uniform intensity of 2I0.
|
Key Takeaways
3. The conditions for bright and dark fringes are given as : Bright fringes x = 4. The distance between any two consecutive bright or dark fringes is known as fringe width and it is given by β =(
|
Newton’s Rings are the circular interference pattern first discovered by physicist Sir Isaac Newton in 1704. It is cosists of concentric bright and dark rings with the point of contact of lens and the glass plate as centre,
The fringes obtained by interference of light waves by using the following arrangement
When a Plano convex lens with large radius of curvature is placed on a plane glass plate such that its curved surface faces the glass plate, a wedge air film (of gradually increasing thickness) is formed between the lens and the glass plate. The thickness of the air film is zero at the point of contact and gradually increases away from the point of contact.
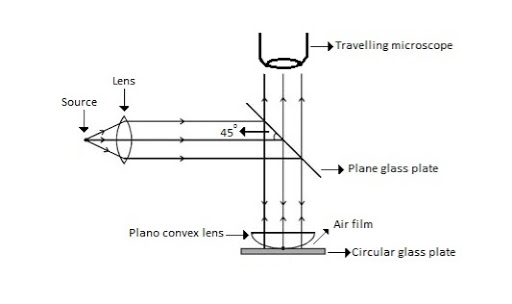
Figure 22: Newton Ring Assembly |
If monochromatic (means light with single wavelength) light is allowed to fall normally on the lens from a source 'S', then two reflected rays R1 (reflected from upper surface of the film) and R2 (reflected from lower surface of the air film) interfere to produce circular interference pattern. This interference pattern has concentric alternate bright and dark rings around the point of contact. This pattern is observed through traveling microscope.
MATHEMATICAL ANALYSIS OF NEWTON’S RING
Figure 23: Mathematical analysis of newton’s ring |
(OL)2 =(O’M)2-(ML)2 ……….(1) R2=(R-t)2 +rn2 R2=R2 +t2-2Rt +rn2 Radius is large as compared to the thickness so t2 is neglected as t2<< R2 R2=R2 +-2Rt +rn2 2Rt =rn2 Thickness of the film t =rn2 /2R ……….(2) THEORY OF FRINGES: The effective path difference between the two reflected rays R1 and R2 for a wedge shaped film from equation ∆ = 2μtcos(r+θ) +λ/2 ……….(3) If the light is incident normally on the lens, r = 0 and near to point of contact θ is small; Therefore near point of contact, (r+θ) approaches to 0 and cos(r+θ)=cos0=1 Therefore ∆ = 2μt+λ/2 ……….(4)
Also At point of contact t = 0 therefore the effective path difference ∆ = λ/2 Which is odd multiple of λ/2 Therefore the Central fringe is dark.
BRIGHT FRINGE: CONDITION OF MAXIMA For the condition of maxima the effective path difference ∆ = ±nλ Using equation (4) ∆ = 2μt+λ/2 we have 2μt+λ/2= ±nλ 2μt = ± (2n-1)λ /2 ……….(5)
DIAMETER OF BRIGHT RINGS we know by equation (2) t =rn2 /2R substitute in equation (5) we have 2μ (rn2 /2R) = ± (2n-1)λ /2 rn2 = ± (2n-1)λR /2μ We know diameter D=2r and for nth fringe Dn=2rn so we have Dn2=± 2(2n-1)λR /μ Dn= The medium enclosed between the lens and glass plate is if air therefore, D= The diameter of bright ring is proportional to square root of odd natural numbers
DARK FRINGE: CONDITION FOR MINIMA For the condition of minima, The effective path difference ∆ =± (2n+1)λ /2 2μt+λ/2 =± (2n+1)λ /2 2μt= ±nλ ……….(7) it is clear that for particular dark or bright fringe t should be constant. Every fringe is the locus of points having equal thickness. Hence the fringes are circular in shape.
DIAMETER OF DARK RINGS we know by equation (2) t =rn2 /2R substitute in equation (7) we have 2μ (rn2 /2R ) = nλ rn2 = nλR/ μ We know diameter D=2r and for nth fringe Dn=2rn so we have Dn2= 4nλR/ μ Dn= The medium enclosed between the lens and glass plate is if air therefore, Dn= The diameter of dark ring is proportional to square root of natural numbers.
SPACING BETWEEN FRINGES The Newton’s rings are not equally spaced because the diameter of ring does not increase in the same proportion as the order of ring and rings get closer and closer as ‘n’ increases. For example the diameter of dark ring is given by Dn= D3 - D2 = D7 – D6 = D10– D9 = From above result we conclude that the fringe width reduces with increase in n.
APPLICATION OF NEWTON’S RING
The diameter of the nth order ring is calculated by subtracting the left and right side position of the microscope. As we know that the square of diameter of nth dark ring is
Therefore the square of diameter of (n+p)th ring is
Subtracting both the above equation
Therefore 2. Determination of Refractive Index of liquid In order to determine the refractive index of liquid the Newton’s ring experiment is first performed for the air medium and the difference in the square of the diameter of (n+p)th and nth dark ring is found as discussed above. After this few drops of liquid of μ refractive index is placed on the glass plate. The plano-convex lens is then placed on the glass plate, as a result a film of liquid is formed between the lens and the plate. The difference in the square of the diameter of (n+p)th and nth dark ring is again calculated in the same manner for the liquid medium. Dividing equation 2.29 by 2.30, we get
3. Newton’s ring with white light If the monochromatic source is replaced by the white light, dark and bright fringes are not produced. Because the diameter of the rings depends upon wavelength and it is proportional to the square root of wavelength. If If the monochromatic source is replaced by the white light superposition of rings take place due to different wavelength. Few coloured rings are seen around dark centre later illumination is seen in the field of view. As shown in below figure.
Figure 24: Newton’s ring with white light
Example: In a Newton’s rings experiment the diameter of the 15th ring was found to be 0.59 cm and that of the 5th ring is 0.336 cm. If the radius of curvature of the lens is 100 cm, find the wave length of the light. Solution: The given data are Diameter of Newton’s 15th ring (D15) = 0.59 cm = 0.59×10–2 m Diameter of Newton’s 5th ring (D5) = 0.336 cm = 0.336 × 10–2 m Radius of curvature of lens (R) = 100 cm = 1 m Wave length of light (λ) = ? Here m is difference between rings = 15-5=10 λ = D2n+m - D2n / 4mR λ = (0.59×10–2 )2- (0.336 × 10–2)2 / 4 x 10 x 1 λ = 0.3481 x10-4 – 0.112896 x10-4 / 40 λ =0.00588 x 10-4 m λ =5880 x 10-10 m λ =5880Å |
Key takeaways
6. Determination of Refractive Index of liquid
s 7. If the monochromatic source is replaced by the white light, dark and bright fringes are not produced. |
DIFFRACTION: FRAUNHOFFER DIFFRACTION DUE SINGLE SLIT
Diffraction
When the light falls on the obstacle whose size is comparable with the wavelength of light then the light bends around the obstacle and enters in the geometrical shadow. This bending of light is called diffraction.
2.8.1 FRAUNHOFFER DIFFRACTION AT SINGLE SLIT
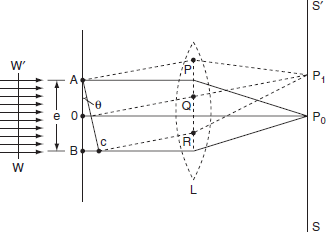
The adjacent figure represents a narrow-slit AB of width ‘e’. Let a plane wavefront of monochromatic light of wavelength '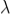 ' is incident on the slit. Let the diffracted light be focused by means of a convex lens on a screen. According to Huygen Fresnel, every point of the wavefront in the plane of the slit is a source of secondary wavelets. The secondary wavelets traveling normally to the slit i.e., along OP0 are brought to focus at -+
' is incident on the slit. Let the diffracted light be focused by means of a convex lens on a screen. According to Huygen Fresnel, every point of the wavefront in the plane of the slit is a source of secondary wavelets. The secondary wavelets traveling normally to the slit i.e., along OP0 are brought to focus at -+
azP0 by the lens. Thus, P0 is a bright central image. The secondary wavelets traveling at an angle '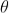 ' are focused at a point P1 on the screen.
' are focused at a point P1 on the screen.
The intensity at the point P1 is either minimum or maximum and depends upon the path difference between the secondary waves originating from the corresponding points of the wavefront.
Figure 25: Fraunhoffer diffraction at single slit
|
Theory: In order to find out the intensity at P1, draw a perpendicular AC on BR. The path difference between secondary wavelets from A and B in direction θ is BC i.e,
So, the phase difference,
Let us consider that the width of the slit is divided into ‘n’ equal parts and the amplitude of the wave from each part is ‘a’. So, the phase difference between two consecutive points
Then the resultant amplitude R is calculated by using the method of vector addition of amplitudes
Figure 26: Mathematical analysis of Fraunhoffer diffraction at single slit The resultant amplitude of n number of waves having same amplitude 'a' and having common phase difference of '
Substituting the value of R = a Substituting As R = n and na = A Therefore R =A Therefore, the Intensity is given by I =R2 = A2 Case (i): Principal Maximum: Eqn (4) takes maximum value for
sinθ = 0 or θ=0 The condition The condition θ=0 means that this maximum is formed by the secondary wavelets which travel normally to the slit along OP0 and focus at P0. This maximum is known as “Principal maximum”. Intensity of Principal maxima
Therefore Imax = R2max = A2 Case (ii): Minimum Intensity positions: Equation (3) takes minimum values for sin
In the above equation (6) n = 0 is not applicable because corresponds to principal maximum. Therefore, the positions according to equation (6) are on either side of the principal maximum. Case (iii): Secondary maximum: In addition to principal maximum at
A2
Because
The values of ' The points of intersection of the two curves gives the values of The points of intersections are |
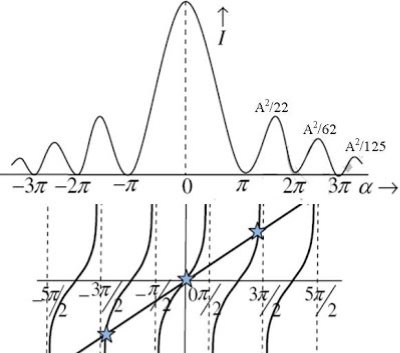
Figure 27: Variation of intensity |
But
and so on. From the above expressions, Imax, I1, I2,I3… it is evident that most of the incident light is concentrated at the principal maximum. |
INTENSITY DISTRIBUTION GRAPH
A graph showing the variation of intensity with '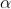 ' is as shown in the adjacent figure
' is as shown in the adjacent figure
Figure 28: Intensity Distribution Graph |
2.8.2 FRAUNHOFER DIFFRACTION AT CIRCULAR APERTURE
Airy in 1835 solved the problem of diffraction at a circular aperture.
When diffraction due to a circular aperture takes place, it forms an intensity pattern. An intensity pattern is formed because of the distribution of amplitude of waves.
An intensity pattern consists of a bright central band surrounded by concentric circular bands of rapidly decreasing intensity. This pattern is known as Airy pattern. The 1st maximum is roughly 1.75% of the central intensity. 84% of the light arrives within the central peak called the airy disc.
Let us consider a circular aperture of diameter AB= d is shown in in figure below. A plane wave front WW' is incident normally on this aperture. Every point on the plane wave front in the aperture acts as a source of secondary wavelets. The secondary wavelets spread out in all directions as diffracted rays in the aperture.
Figure 29: Fraunhofer diffraction at circular aperture
|
Place a convex lens (L) between the aperture and the screen. The screen is at the focal plane of the convex lens. The diffracted secondary wavelets are converged on the screen SS' through a convex lens L. These diffracted rays traveling normal to the plane of aperture [i.e., along CP0] are get converged at P0.
All these waves coming from circular aperture travel same distance to reach P0 and there is no path difference between these rays. Hence a bright spot is formed at P0 known as Airy's disc. P0 corresponds to the central maximum.
Now consider the secondary waves traveling at an angle Now consider a point P1 on the ring, the intensity of light at P1 depends on the path difference between the waves at A and B to reach P1. The path difference is given by BD = ABsin The diffraction due to a circular aperture is similar to the diffraction due to a single slit. Hence, the intensity at P1 depends on the path difference dsin If the path difference is an integral multiple of for minima dsin for maxima dsin Where n = 1, 2, 3... etc. n = 0 corresponds to central maximum. The Airy disc is surrounded by alternate bright and dark concentric rings, called the Airy's rings. The intensity of the dark ring is zero and the intensity of the bright ring decreases as we go radially from P0 on the screen. If the collecting lens (L) is very near to the circular aperture or the screen is at a large distance from the lens, then sin Where, f is the focal length of the lens. Also from the condition for first secondary minimum [using equation (1)] sin Equations (3) and (4) are equal
So x = But according to Airy, the exact value of x is x = Using equation (6) the radius of Airy's disc can be obtained. Also from this equation we know that the radius of Airy's disc is inversely proportional to the diameter of the aperture. Hence by decreasing the diameter of aperture, the size of Airy's disc increases. |
Key Takeaways
- The intensity in case of Fraunhoffer diffraction at single slit at the point P1 is either minimum or maximum and depends upon the path difference between the secondary waves originating from the corresponding points of the wavefront.
- Intensity is given by I =R2 = A2
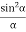
Limit of Resolution:
The minimum distance between two points on the object so that their images (as produced by the optical instrument) are just seen as separate from each other is called limit of resolution of the optical instrument.
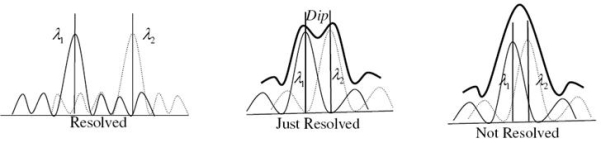
Statement: Two sources are resolvable by an optical instrument when the central maximum of one diffraction pattern falls over the first minimum of the other diffraction pattern and vice versa.
Let us consider the resolution of two wavelengths by a grating. When the difference in wavelengths is smaller and such that the central maximum of the wavelength coincides with the first minimum of the other as shown in figure, then the resultant intensity curve is as shown by the thick curve. The curve shows a distinct dip in the middle of two central maxima. Thus the two wavelengths can be distinguished from one another and according to Rayleigh they are said to be “Just Resolved”.
If the difference in wavelengths is such that their principal maxima are separately visible, then there is a distinct point of zero intensity in between the two wavelengths. Hence according to Rayleigh they are said to be “Resolved”.
When the difference in wavelengths is so small that the central maxima corresponding to two wavelengths come still closer as shown in figure, then the resultant intensity curve is quite smooth without any dip. This curve is as if there is only one wavelength somewhat bigger and stronger.
Hence according to Rayleigh the two wavelengths are “Not Resolved”.
Thus the two spectral lines can be resolved only up to a certain limit expressed by Rayleigh Criterion.
Figure 30: Rayleigh Criterion
|
APPLICATION TO VISION
Visual acuity is typically measured with the use of a standard eye chart called the Snellen chart. What are the factors which limit the resolution of human vision? To examine whether diffraction is the limiting factor, it is interesting to compare this standard of resolution with the limits imposed by diffraction.
The Rayleigh criterion is the generally accepted criterion for the minimum resolvable detail - the imaging process is said to be diffraction-limited when the first diffraction minimum of the image of one source point coincides with the maximum of another.
The acuity of our vision is limited because light passes through the pupil, the circular aperture of our eye. Be aware that the diffraction-like spreading of light is due to the limited diameter of a light beam, not the interaction with an aperture. Thus light passing through a lens with a diameter  shows this effect and spreads, blurring the image, just as light passing through an aperture of diameter
shows this effect and spreads, blurring the image, just as light passing through an aperture of diameter  does. So diffraction limits the resolution of any system having a lens or mirror. Telescopes are also limited by diffraction, because of the finite diameter
does. So diffraction limits the resolution of any system having a lens or mirror. Telescopes are also limited by diffraction, because of the finite diameter  of their primary mirror.
of their primary mirror.
If all parts of an imaging system are considered to be perfect, then the resolution of any imaging process will be limited by diffraction. Considering the single slit expression above, then when the wavelength is equal to the slit width, the angle for the first diffraction minimum is 90°. This means that the wave is spread all the way to the plane of the slit and will not contain resolvable information about the source of the wave. This leads to the simplified statement that the limit of resolution of any imaging process is going to be on the order of the wavelength of the wave used to image it.
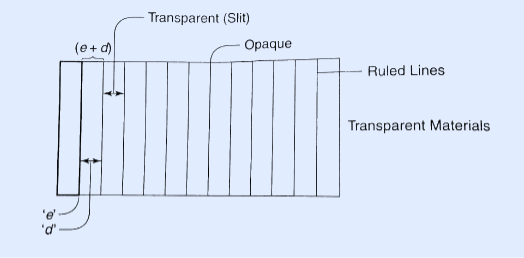
A set of large number of parallel slits of same width and separated by opaque spaces is known as diffraction grating.
Diffraction gratings are much more effective than prisms for dispersing light of different wavelengths so they are used almost exclusively in instruments designed to detect and identify characteristic spectral lines. There is nothing mysterious about these devices.
Fraunhofer used the first grating consisting of a large number of parallel wires placed side by side very closely at regular separation. Now the gratings are constructed by ruling the equidistance parallel lines on a transparent material such as glass with fine diamond point. The ruled lines are opaque to light while the space between the two lines is transparent to light and act as a slit.
Figure 31: Plane Transmission Grating |
Let ‘e’ be the width of line and ‘d’ be the width of the slit.
Then (e + d) is known as grating element.
If N is the number of lines per inch on the grating then
(𝑒+𝑑)=1𝑖𝑐ℎ=2.54𝑐𝑚
(𝑒+𝑑)=2.54𝑐𝑚/𝑁
Commercial gratings are produced by taking the cost of actual grating on a transparent film like that of cellulose acetate. Solution of cellulose acetate is poured on a ruled surface and allowed to dry to form a thin film, detachable from the surface. This film of grating is kept between the two glass plates.
Example: A parallel beam of monochromatic light of wavelength 500nm is inclined normally on a plane diffraction grating 4000 per centimetre. Calculate the angle of diffraction for first order principal maximum. Solution: Given: number of lines per cm =4000 Grating element e+b = 1/4000 cm = 2.5 x 10-6m λ=500 nm Order n =1 (e+b) sinθ =nλ sinθ = nλ / (e+b) sinθ = 1 x 500 x 10-9 / 2.5 x 10-6 sinθ =0.2 θ =sin-1 0.2 θ = 11.5o
|
RESOLVING POWER OF DIFFRACTION GRATING
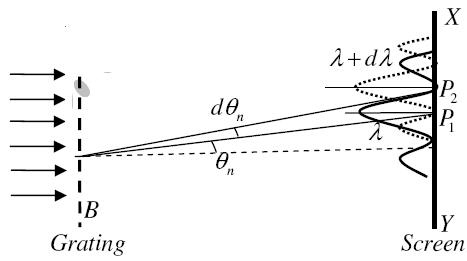
It is defined as the capacity of a grating to form separate diffraction maxima of two wavelengths which are very close to each other
It is measured by λ/dλ where dλ is the smallest difference in two wavelengths which are just resolvable by grating and λ is the wavelength of either of them or mean wavelength.
Figure 32: Resolving Power of Diffraction Grating |
Let AB represent the surface of a plane transmission grating having grating element (e+d) and N total number of slits. Let a beam of light having two wavelengths by λ and dλ is normally incident on the grating. Let P1 is nth primary maximum of a spectral line of wavelength λ at an angle of diffraction According to Rayleigh criterion, the two wavelengths will be resolved if the principal maximum λ+dλ of nth order in a direction θ+dθ falls over the first minimum of nth order in the same direction θ+dθ. Let us consider the first minimum of l of nth order in the direction θ+dθ as below. The principal maximum of (e+d)sinθ =nλ ………………(1) The equation of minima is N(e+d)sinθ = mλ ………………(2)
Where m takes all integers except 0, N, 2N, …, nN, because for these values of m, the condition for maxima is satisfied. Thus first minimum adjacent to nth principal maximum in the direction θ+dθ can be obtained by substituting the value of ‘m’ as (nN+1). Therefore, the first minimum in the direction of θ+dθ is given by N(e+d)sin(θ+dθ) = (nN+1)λ (e+d)sin(θ+dθ) = (n+ The principal maximum of λ+dλ in direction θ+dθ is given by (e+d)sin(θ+dθ) = n(λ+dλ) ………………(4) Dividing eqn(3) by equation (4), we get (n+ nλ +
Resolving Power = Thus the resolving power is directly proportional to (i) The order of the spectrum ‘n’ (ii) The total number of lines on the grating ‘N
Example: A grating has 1100 lines ruled on it. What is difference between the two wavelengths that just appear resolved in the first order spectrum in the region of wavelength λ = 660 nm? Solution: N = 1100 nm λ = 660 x 10-9 m n = 1 R = λ /dλ =Nn dλ = λ /Nn dλ = 660 x 10-9 / 1100 x 10-9 x 1 dλ = 0.6 x 10-9 m
|
Key Takeaways
- A set of a large number of parallel slits of the same width and separated by opaque spaces is known as a diffraction grating.
- Resolving power of diffraction is defined as the capacity of a grating to form separate diffraction maxima of two wavelengths that are very close to each other
- Resolving Power =
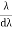 = nN
= nN
References
- Fundamentals of optics-Jenkins and White. McGraw Hill Publication
- A Text Book of Optics Subrahmanyam, BrijIal, S. Chand Publication
- Optics by Ajay Ghatak
- Engineering physics - Avadhanalu and Kshirsagar, S.Chand Publication