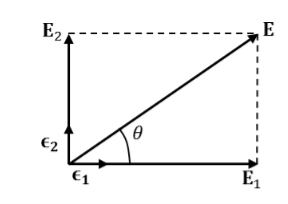
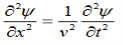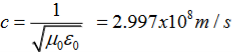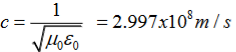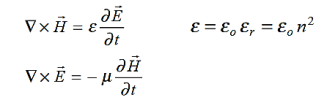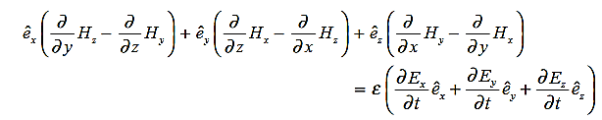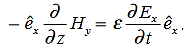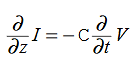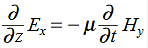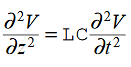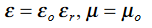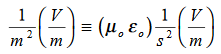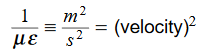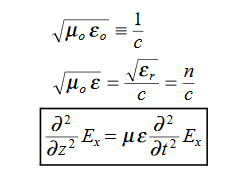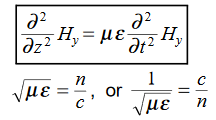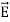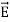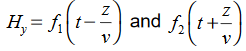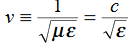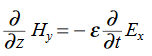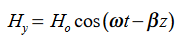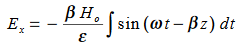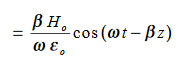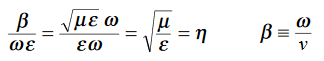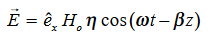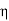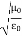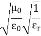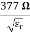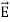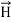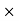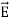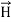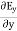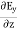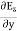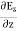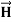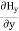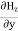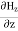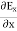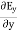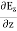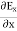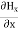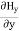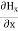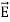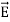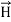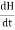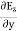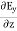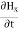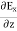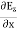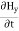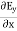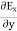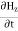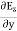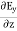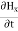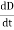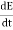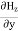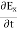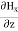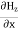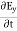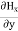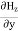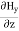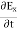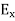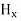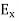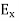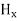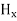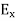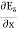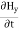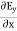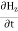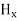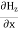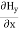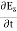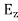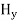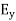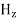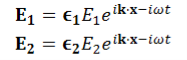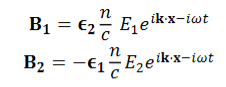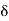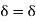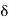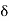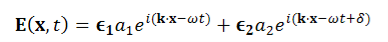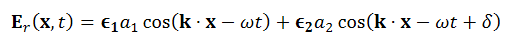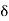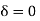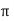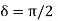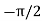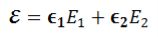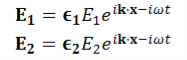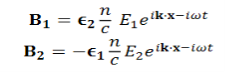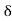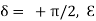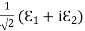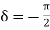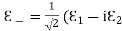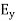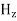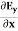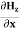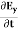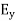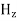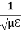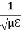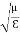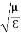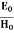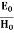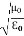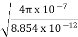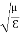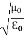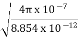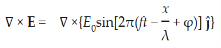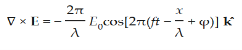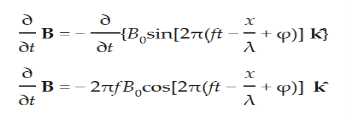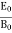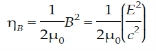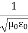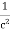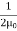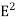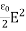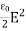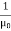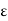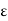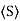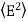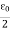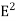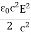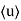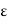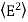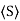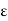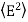UNIT-4
ELECTROMAGNETIC WAVES
Wave is nothing but a pattern of disturbance which propagates and carry energy with it. You can produce a wave on a rope by moving one end of the rope up and down. The wave produces on rope needs a medium to propagate and here medium is rope itself. This type of waves is known as mechanical waves. But in the case of Electromagnetic waves, they don't need a medium to propagate. Electromagnetic waves are waves that are created as a result of variations of electric field and a magnetic field. Or we can say that Electromagnetic waves are nothing but changing magnetic and electric fields. Electromagnetic waves are also known to be solutions of Maxwell's equations. And Maxwell's equations are the fundamental equations of electrodynamics. Electromagnetic waves can transmit energy and travel through a vacuum.
Light waves are examples of electromagnetic waves. Generally, Electromagnetic waves are shown by a sinusoidal graph.
|
Figure 1: Electromagnetic waves
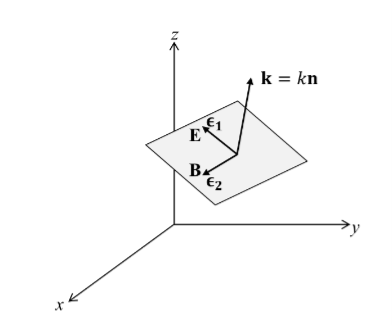
As shown in figure Electromagnetic waves consist of time-varying electric and magnetic fields and they are perpendicular to each other and these both fields are also perpendicular to the direction of propagation of waves.
Maxwell’s four equations are given by
∇·E = ρ/ε0 (1) ∇×E = −∂B/∂t (2) ∇×H = J + ∂D/∂t (3) ∇·B = 0 (4) ∇=(∂/∂x, ∂/∂y, ∂/∂z) E is the electric vector B is the magnetic induction ρ is the electric charge density j is the electric current density ε0 is the permittivity of free space c is the speed of light.
In addition to Maxwell equations, the following identities are useful:
J = σE (5) D = εE (6) B = μH (7)
Here, D is the electric displacement H is the magnetic vector σ is the specific conductivity ε is the dielectric constant (or permittivity) μ is the magnetic permeability (a) No condition current i.e σ=0, thus J=0 ( J=σE) ∇ x E= -dB/dt or ∇ x E= -μ dH/dt because B = μH (13) |
WAVE EQUATION IN TERMS OF ELECTRIC FIELD INTENSITY, E
Now taking curl of second Maxwell’s equation (13) ,we get ∇ (∇ .E)-∇2E= -μ d/dt (∇ x H) (16) Substituting equations (13) and (14) in equations (16) ,we get |
WAVE EQUATION IN TERMS OF MAGNETIC FIELD INTENSITY, H
Take curl of fourth Maxwell’s equation (14) ,we get ∇x(∇xH)=ε d/dt(∇xE) Applying standard vector identity that is [∇*(∇*H)=∇ (∇.H)-∇2H] On left side of above equation , we get ∇(∇.H)-∇2H= ε d/dt(∇xE) (18) Substituting equations (14) and (13) in equation(18) ,we get -∇2H= – μεd/dt(dH/dt) Or ∇2H=με d2H/dt2 (19) Equations (19) is the required wave equation in terms of magnetic field intensity, H and this is the law that H must obey For vacuum μ=μ0 and ε=ε0, equations (17) and (19) will become ∇2 E=μ0ε0 d2E/dt2 (20) And ∇2H= μ0ε0 d2H/dt2 (21) This leads to an expression for the velocity of propagation |
From equation both equations (20) and (21) have the form of the general wave equation for a wave
Let us rewrite the equation (20) and (21) for one dimension. Or d 2 E/dx2 = μ0ε0 d 2 E/dt2 (22) d2H/dx2 = μ0ε0 d2H/dt2 (23) The simplest solutions to the differential equations (22) and (23) are sinusoidal wave functions: E(x) = Emax cos(kx-t) (24) B(x) = Bmax cos(kx-t) (25) where k = 2π/λ is the wavenumber , ω = 2πƒ is the angular frequency, λ is the wavelength, f is the frequency and ω /k=f=v= c. |
Key Takeaways
- Wave is nothing but a pattern of disturbance which propagates and carries energy with it.
- In the case of Electromagnetic waves, they don't need a medium to propagate. Electromagnetic waves are waves that are created as a result of variations of electric field and a magnetic field.
- Electromagnetic waves are also known to be solutions of Maxwell's equations.
- Wave equation in terms of electric field intensity E for free space is given by ∇2 E=μ0ε0 d2E/dt2
- Wave equation in terms of magnetic field intensity H for free space is given by ∇2H= μ0ε0 d2H/dt2
- (x,t) traveling with speed c in free space is given by
|
Solutions of Maxwell’s Equations - Uniform Plane Waves
The sources of time varying electromagnetic fields are time varying charges and currents, whether man-made or naturally occurring. However, examination of Maxwell’s equations shows that, even in empty space (with no sources), and fields cause each other. This means that, although these fields must originate in source regions, they can propagate through source-free regions. Because solutions in source regions are very hard to obtain, let us consider what kind of fields can exist in source-free regions.
|
These equations are still very complicated (4 different partial derivatives). Let’s try to find simple solutions. We do this by making assumptions. After finding simplest solutions, we:
(i) Find what kind of source would generate this type of field (waves).
(ii) Show that these simple solutions are useful approximations to real electromagnetic waves.
Assumption for Solution:
Can we find a solution such that:
1.) No variation exists in x and y directions.
2.)  or
or 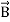 also is oriented along one of the axes.
also is oriented along one of the axes.
Ampere’s Law becomes:
or, with our assumptions:
Compare for transmission line:
In a similar manner,
Faraday’s Law becomes:
Thus, if
Substitute from (2),
We get
This is called the wave equation. Compare for transmission line: (same).
We will assume dielectric media; lossless:
Dimensional analysis:
In the units we are using:
By exactly the same method, we also get:
For example, the same equation is true for
are the solutions
t is important to note that f1 and f2 can be any function. The field we find directly from the equation:
Suppose
Differentiate (3) with respect to z
Integrate with respect to time
This leads to a new quantity that relates the electric and magnetic fields:
Rewriting: Units of
Note that The directions of the vectors are such that:
This vector “Plane” refers to the fact that, at any instant in time, the surfaces of constant phase are planes (here, constant).
|
“Uniform” means no variation in transverse direction. The wave derived here is one oscillating at a single frequency. The frequency is determined by the source. If the source has multiple frequencies, so will the wave. In communications, modulating a carrier wave results in multiple frequencies. But before we can study such fields, we must thoroughly understand single frequency sinusoidal waves.
In this section we will study the variation of field of 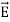 and
and 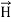 of an em plane wave with space and time.
of an em plane wave with space and time.
From Maxwell’s equation for free space, we have
|
Time Variation of 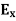 and
and 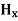
Key Takeaways
- A wave in which the values of variable are constant in a plane perpendicular to the direction of propagation of the wave is called plane wave. These planes may also termed as wave fronts.
- In an electromagnetic wave, electric and magnetic field vectors are perpendicular to each other and at the same time are perpendicular to the direction of propagation of the wave. This nature of electromagnetic wave is known as Transverse nature.
Key Takeaways
We know that wave equations are given by ∇2 E=με d2E/dt2 …………..(1) And ∇2H= με d2H/dt2 …………..(2) The electric and magnetic vectors in an em waves are given by:
It is evident therefore that:
and
Substitute the values of -ik E0eik (vt-x) =- μ (ikv) H0eik (vt-x) Which gives E0 =- μvH0 But v = E0 = μ x E0 =
That is the relation between the values of the electric and magnetic vectors as determined by the relative values μ and Ɛ. In other words, the ratio of the electric and magnetic vectors is directly proportional to the square root of the ratio of μ and Ɛ.
E0 =377 H0 or E =377H It shows that the values of electric vector at any instant in the em wave are about 377 times the values of magnetic vector. It is because of this reason that while discussing the behaviour of light as em wave, we prefer the use of the electric vector. |
Key Takeaways
|
Key Takeaways
- A wave’s energy is proportional to its amplitude squared.
- For an electromagnetic wave in free space, half the energy is in the electric field and half is in the magnetic field
- The electric energy density is given by
ηB = 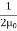 μ0ε0
μ0ε0 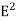 =
= 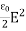
4. The total energy density of an electromagnetic wave.
η = ε0E2
References
- Prabir K. Basu & Hrishikesh Dhasmana, ‘Electromagnetic Theory’.
- Khunita, ‘Fundamentals of Electromagnetic Theory’.
- S.P. Puri, ‘Classical Electrodynamics’, Tata McGraw Hill
- Gupta & Gaur, ‘Engineering Physics’, Dhanpat Rai.
- Malik and Singh, ‘Engineering Physics’, Tata McGraw Hill.