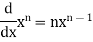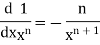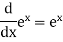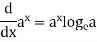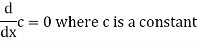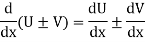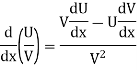Unit-3
Calculus
The rate of change of one variable of function with respect to another on which it depends is called the derivative of the function.
A derivative is the limit of the ratio of the small increment in one variable of the function corresponding to a small increment in the argument (other variable) as the later tends to zero.

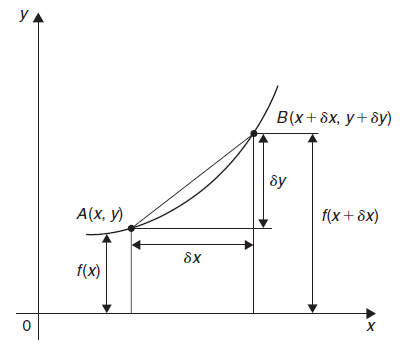
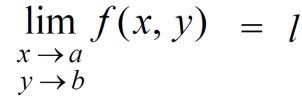
Differentiation from first principal-
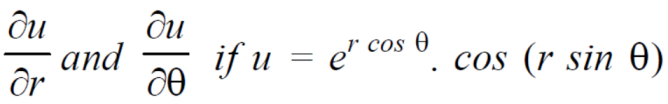
A and B are the two point on a curve representing small increment in the x and y directions respectively.
Gradient of chord-
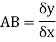
However-
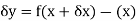
Hence-
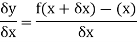
Here 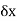 which approaches to 0,
which approaches to 0, 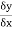 approches a limiting value of the gradient of the chord approaches the gradient of the tangent A.
approches a limiting value of the gradient of the chord approaches the gradient of the tangent A.
When determining the gradient of a tangent to a curve there are two notations used. The gradient of the curve at A can either be written as,
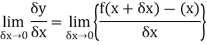
Where
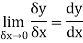
Or we can write it as-
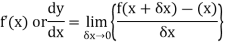
Example: Differentiate the function f(x) = 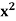 by using the first principal method.
by using the first principal method.
Solution.
We know that-

Here
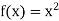
Substituting ( for x gives-
for x gives-
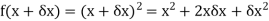
Hence-
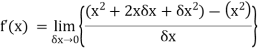
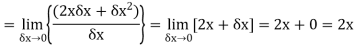
Limits-
The function f(x,y) is said to tend to limit ‘l’ , as x →a and y→bIff the limit is dependent on point (x,y) as x →a and y→b
We can write this as,
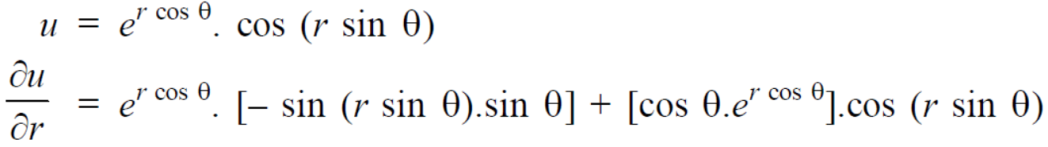
Example-1: evaluate the 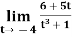
Solution. We can simply find the Solutionution as follows,
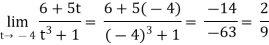
Example-2: evaluate 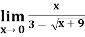
Solution.
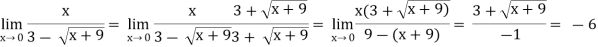
Example-3: evaluate 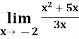
Solution.

Increment-
Increment of a variable means the difference of initial value from the final value
Increment = final value – initial value
Let x change its value from 2 to 8, increment of x = 8 – 2 = 6
Note- increment can be negative or positive.
Here we will denote the increment of x by 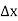
If in y = f(x), the independent variable x changes to 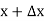 then the increment of x =
then the increment of x = 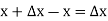
So y = f(x) changes to y = f(x + 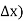
Increment of y = f(x + 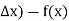
Then the increment ratio-
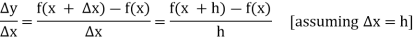
If the ratio 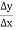 tends to a limit, as
tends to a limit, as  ® 0 from either side, then this limit is known as the derivative of
® 0 from either side, then this limit is known as the derivative of
y [ = f(x)] with respect to x.
A function y = f(x) is said to be derivable at x if
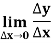
Or
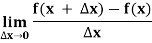
Or
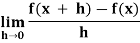
Derivative of y = f(x) with respect to x is denoted by dy/dx or 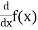
Some useful derivatives-
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
Example: Find dy/dx of the following functions-
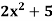
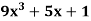
Sol.
Let y = 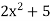
Then-
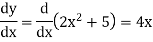
And
Let y = 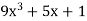
Then-
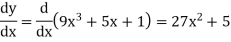
Example: Differentiate 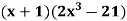 with respect to x.
with respect to x.
Sol.
Let 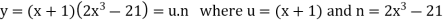
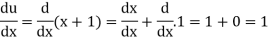

Now
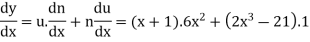
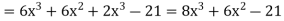
Example: if 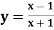 then find dy/dx.
then find dy/dx.
Solution.
Suppose y = u/v where u = x - 1 and v = x + 1
Then

And

So that-
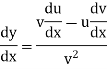
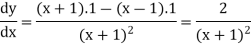
Derivative of function of a function-
If y = f(z), z = 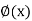 then y = f{
then y = f{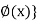
Now if y = f(z) and z = z = 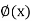 then-
then-
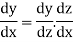
Derivative of logarithmic function and exponential function-
If y = log x then its derivative will be-
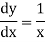
If y = 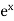 then its derivative-
then its derivative-
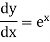
Note- derivative of a constant is always zero.
Example: if y = 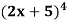 then find dy/dx.
then find dy/dx.
Sol.
Suppose z = 
Now-
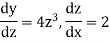
So that-
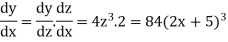
Example: if y = 
Sol.
Suppose y = 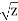 where z =
where z = 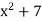
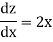
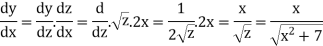
Example: If y = log loglog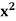 then find dy/dx.
then find dy/dx.
Sol.
Suppose y = log u where u = log v and v = log 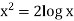
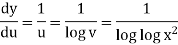
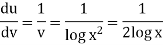
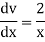
So that-
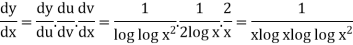
Example: if y = 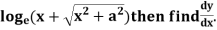
Sol.
Let y = log u where u = 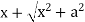
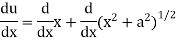
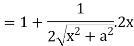
Now
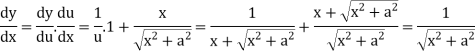
Example: find the derivative of the function f(x) = 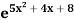 .
.
Sol.
Let y = f(x) then
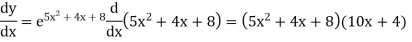
Example: Find the derivative of 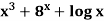
Sol.
Let y = 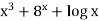 then-
then-
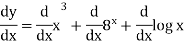
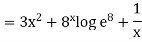
Second order derivative-
The derivative of dy/dx is known as the second order derivative of y.
It is denoted by 
Example: if y = log x/ x a then find 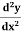
Solution. First we will find the first derivative-

Now
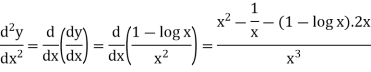
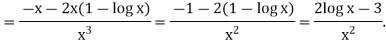
Example: if y = 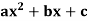 then find
then find 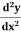
Sol.
Here
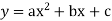
Difference with respect to x, we get-
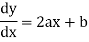
Now
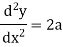
Example: if y = 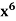 then find
then find 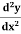 .
.
Sol.
Here
y = 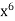
Then
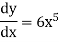

Partial differentiation
First order partial differentiation-
Let f(x, y) be a function of two variables. Then the partial derivative of this function with respect to x can be written as 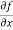 and defined as follows:
and defined as follows:
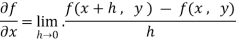
Now the partial derivative of f with respect to f can be written as  and defined as follows:
and defined as follows:
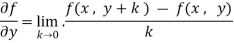
Note:
1. While calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating, as constant.
2. We apply all differentiation rules.
Higher order partial differentiation-
Let f(x , y) be a function of two variables. Then its second-order partial derivatives, third order partial derivatives and so on are referred as higher order partial derivatives.
These are second order four partial derivatives:
(a) 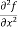 =
= 
(b) 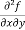 =
= 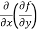
(c) 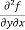 =
= 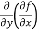
(d) 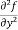 =
= 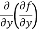
b and c are known as mixed partial derivatives.
Similarly we can find the other higher order derivatives.
Example-1: Calculate  and
and 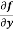 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Sol. To calculate 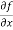 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
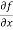 =
=  [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 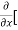 3x³] -
3x³] -  5y²] +
5y²] + 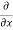 [2xy] -
[2xy] -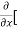 8x] +
8x] +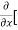 4y] -
4y] - 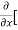 20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
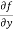 =
= 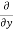 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 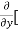 3x³] -
3x³] - 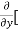 5y²] +
5y²] + 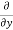 [2xy] -
[2xy] -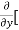 8x] +
8x] +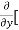 4y] -
4y] - 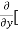 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Example-2: Calculate 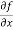 and
and 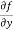 for the following function
for the following function
f( x, y) = sin(y²x + 5x – 8)
Sol. To calculate 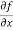 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
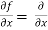 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)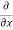 (y²x + 5x – 8)
(y²x + 5x – 8)
= (y² + 50)cos(y²x + 5x – 8)
Similarly partial derivative of f(x,y) with respect to y is,
 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)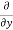 (y²x + 5x – 8)
(y²x + 5x – 8)
= 2xy cos(y²x + 5x – 8)
Example-3: Obtain all the second order partial derivative of the function:
f( x, y) = ( x³y² - xy⁵)
sol.
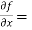 3x²y² - y⁵,
3x²y² - y⁵, 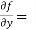 2x³y – 5xy⁴,
2x³y – 5xy⁴,
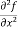 =
= 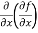 = 6xy²
= 6xy²
 =
= 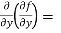 2x³ - 20xy³
2x³ - 20xy³
 =
=  = 6x²y – 5y⁴
= 6x²y – 5y⁴
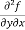 =
= 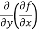 = 6x²y - 5y⁴
= 6x²y - 5y⁴
Example-4: Find

Sol. First we will differentiate partially with respect to r,
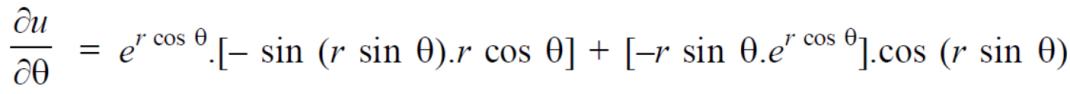
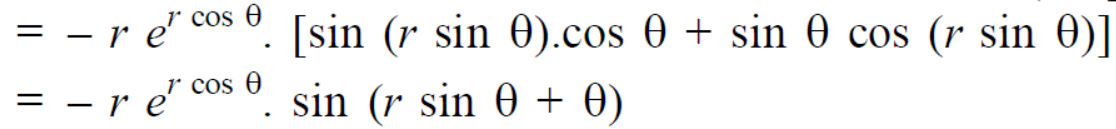
Now differentiate partially with respect to θ, we get
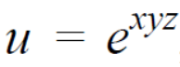
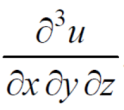
Example-5: if,
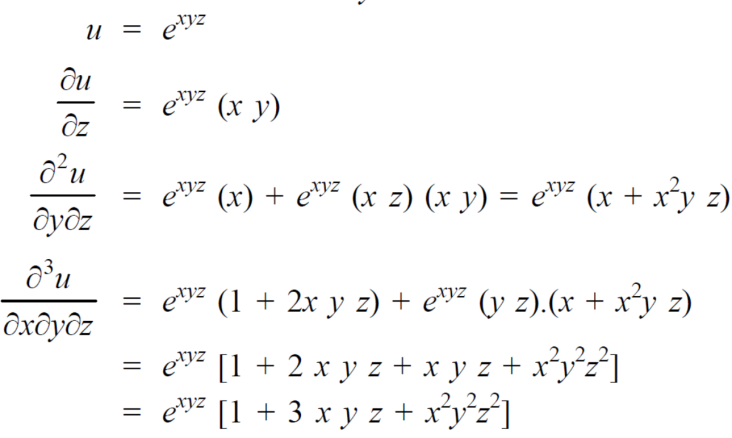
then find.
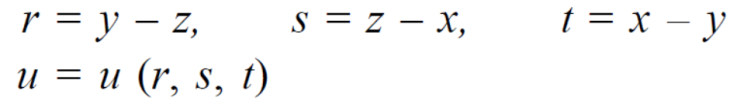
Sol-
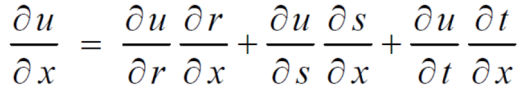
Example-6: if 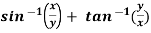 , then show that-
, then show that- 
Sol. Here we have,
u = 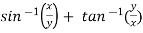 …………………..(1)
…………………..(1)
now partially differentiate eq.(1) w.r to x and y , we get
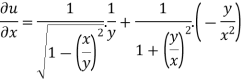
= 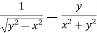
Or
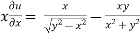 ………………..(2)
………………..(2)
And now,
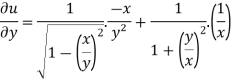
= 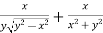
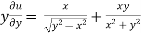 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
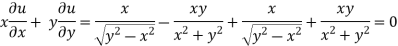
Hence proved.
Key takeaways-
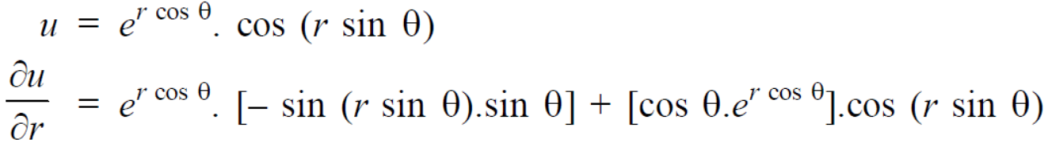
2. Increment of a variable means the difference of initial value from the final value
Increment = final value – initial value
3. the increment ratio-

4. A function y = f(x) is said to be derivable at x if
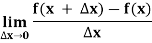
5. Derivative of y = f(x) with respect to x is denoted by dy/dx or 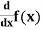
6. 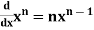
7. 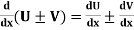
8. 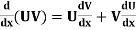
9. 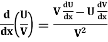
10. While calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating, as constant.
Homogeneous function - A function f(x,y) is said to be homogeneous of degree n if,
f(kx, ky) = kⁿf(x, y)
Here, the power of k is called the degree of homogeneity.
Or
A function f(x,y) is said to be a homogenous function in which the power of each term is the same.
Example:
1. The function-
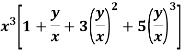
Euler’s theorem-
Statement – if u = f(x, y) be a homogeneous function in x and y of degree n , then
x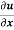 + y
+ y 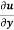 = nu
= nu
Proof:
Here u is a homogeneous function of degree n,
u = xⁿ f(y/x) ----------------(1)
Partially differentiate equation (1) with respect to x,
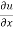 = n
= n f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).( )
)
Now multiplying by x on both sides, we get
x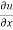 = n
= n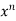 f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).(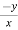 ) ---------- (2)
) ---------- (2)
Again partially differentiate equation (1) with respect to y,
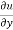 = xⁿ f’(y/x).
= xⁿ f’(y/x).
Now multiplying by y on both sides,
y 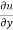 = xⁿ f’(y/x).
= xⁿ f’(y/x). ---------------(3)
---------------(3)
By adding equation (2) and (3),
x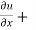 y
y 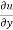 = n
= n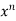 f(y/x) + + xⁿ f’(y/x).(
f(y/x) + + xⁿ f’(y/x).(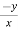 ) + xⁿ f’(y/x).
) + xⁿ f’(y/x).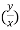
x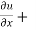 y
y 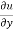 = n
= n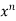 f(y/x)
f(y/x)
Here u = f( x, y) is homogeneous function, then - u = 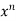 f(y/x)
f(y/x)
Put the value of u in equation (4),
x y
y 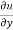 = nu
= nu
Which is the Euler’s theorem.
Let’s understand Eulers’s theorem by some examples:
Example1-If u = x²(y-x) + y²(x-y), then show that  -2 (x – y)²
-2 (x – y)²
Solution - here, u = x²(y-x) + y²(x-y)
u = x²y - x³ + xy² - y³,
now differentiate u partially with respect to x and y respectively,
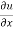 = 2xy – 3x² + y² --------- (1)
= 2xy – 3x² + y² --------- (1)
 = x² + 2xy – 3y² ---------- (2)
= x² + 2xy – 3y² ---------- (2)
Now adding equation (1) and (2), we get
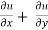 = -2x² - 2y² + 4xy
= -2x² - 2y² + 4xy
= -2 (x² + y² - 2xy)
= -2 (x – y)²
Example2- If u = xy + sin(xy), show that 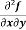 =
= 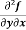 .
.
Solution – u = xy + sin(xy)
 = y+ ycos(xy)
= y+ ycos(xy)
 = x+ xcos(xy)
= x+ xcos(xy)
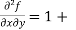 x (- sin(xy).(y)) + cos(xy)
x (- sin(xy).(y)) + cos(xy)
= 1 – xysin(xy) + cos(xy) -------------- (1)
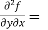 1 + cos(xy) + y(-sin(xy) x)
1 + cos(xy) + y(-sin(xy) x)
= 1 – xysin(xy) + cos(xy) -----------------(2)
From equation (1) and (2),
 =
= 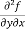
Example-3: If u(x,y,z) = log( tan x + tan y + tan z) , then prove that ,
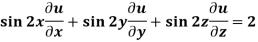
Sol. Here we have,
u(x,y,z) = log( tan x + tan y + tan z) ………………..(1)
diff. eq.(1) w.r.t. x , partially , we get
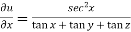 ……………..(2)
……………..(2)
diff. eq.(1) w.r.t. y , partially , we get
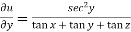 ………………(3)
………………(3)
diff. eq.(1) w.r.t. z , partially , we get
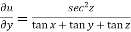 ……………………(4)
……………………(4)
Now multiply eq. 2 , 3 , 4 by sin 2x , sin 2y , sin 2z respectively and adding , in order to get the final result,
We get,
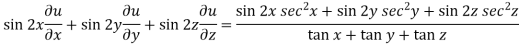
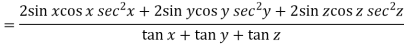

So that,

Total differentials-
When we measure the rate of change of the dependent variable owing to any change in a variable on which it depends, when none of the variable is assumed to be constant.
Let the function, u = f( x, y), such that x = g(t) , y = h(t)
ᵡ Then we can write,
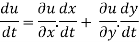
= 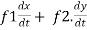
This is the total derivative of u with respect to t.
Change of variable-
If w = f (x, y) has continuous partial variables fx and fyand if x = x (t), y = y (t) are
Differentiable functions of t, then the composite function w = f (x (t), y (t)) is a
Differentiable function of t.
In this case, we get,
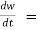 fx(x (t), y (t)) x’(t)+ fy(x(t), y (t)) y’(t).
fx(x (t), y (t)) x’(t)+ fy(x(t), y (t)) y’(t).
Example-:1 let q = 4x + 3y and x = t³ + t² + 1 , y = t³ - t² - t
Then find 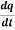 .
.
Sol:
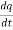 . =
. = 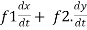
Where,
f1 = 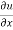 , f2 =
, f2 = 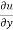
In this example f1 = 4 , f2 = 3
Also,
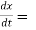 3t² + 2t
3t² + 2t 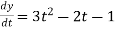
 4(3t² + 2t) + 3(
4(3t² + 2t) + 3(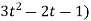
= 21t² + 2t – 3
Example-2: Find 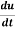 if u = x³y⁴ where x = t³ and y = t².
if u = x³y⁴ where x = t³ and y = t².
Sol. as we know that by definition,  =
= 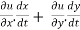
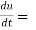 3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
Example-3: if w = x² + y – z + sintand x + y = t, find
(a) 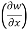 y,z
y,z
(b)  t, z
t, z
Sol. With x, y, z independent, we have
t = x + y, w = x²+ y - z + sin (x + y).
Therefore,
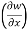 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y) (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
thus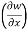 t, z = 2x - 1
t, z = 2x - 1
Example-4: If u = u( y – z , z - x , x – y) then prove that 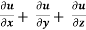 = 0
= 0
Sol. Let,

Then,
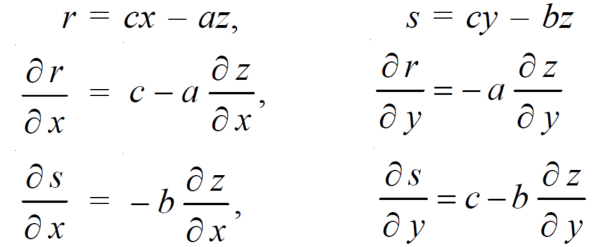
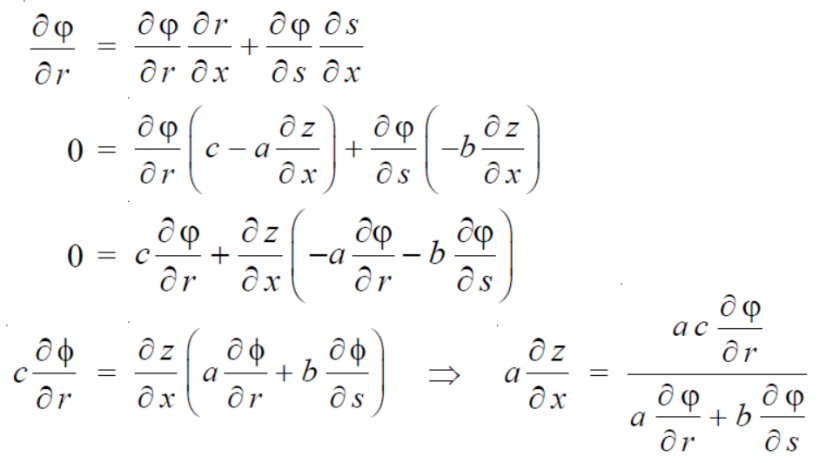
By adding all these equations we get,
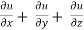 = 0
= 0
hence proved.
Example-5: if φ( cx – az , cy – bz) = 0 then show that ap + bq = c
Where p = 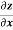 q =
q = 
Sol. We have,
φ( cx – az , cy – bz) = 0
φ( r , s) = 0
where,
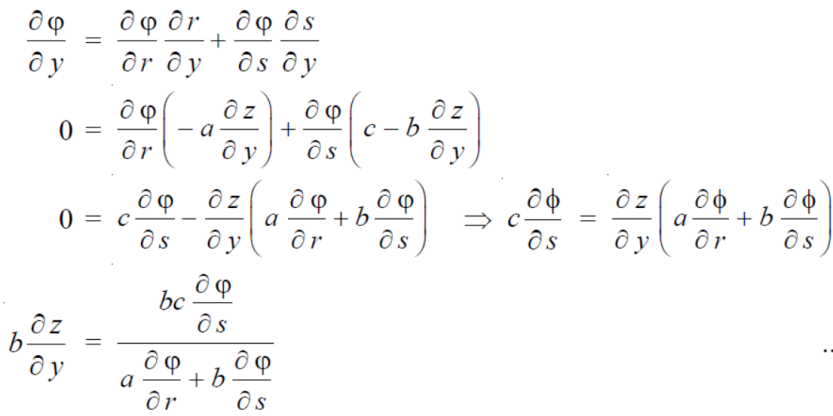
We know that,
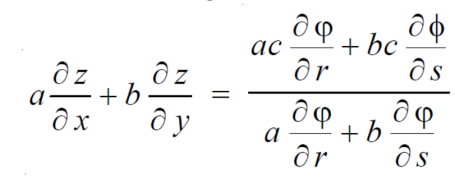
Again we do,

By adding the two results, we get
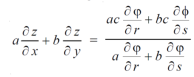
Example-6: If z is the function of x and y , and x = 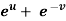 , y =
, y = 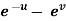 , then prove that,
, then prove that,
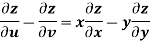
Sol. Here , it is given that, z is the function of x and y & x , y are the functions of u and v.
So that,
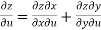 ……………….(1)
……………….(1)
And,
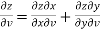 ………………..(2)
………………..(2)
Also there is,
x = 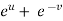 and y =
and y = 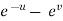 ,
,
now,
 ,
, 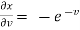 ,
,  ,
, 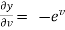
From equation(1) , we get
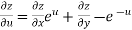 ……………….(3)
……………….(3)
And from eq. (2) , we get
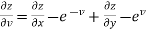 …………..(4)
…………..(4)
Subtracting eq. (4) from (3), we get
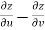 =
= 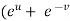 )
)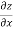 – (
– (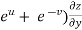
= x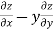
Hence proved.
Maximum and minimum-
A function f(x) is said to be maximum at x = a if f(a) is greater than every other value of f(x) in the immediate neighbourhood of x = a (i.e., f(x) ceases to increase but begins to increase at x = a. Similarly the minimum value of f(x) will be that value at x = b which is less than other values in the immediate neighbourhood of x = b.
Maxima and minima of function of two variables-
As we know that the value of a function at maximum
point is called maximum value of a function. Similarly the value of a function at minimum point is called minimum value of a function.
The maxima and minima of a function is an extreme biggest and extreme smallest point of a function in a given range (interval) or entire region. Pierre de Fermat was the first mathematician to discover general method for calculating maxima and minima of a function. The maxima and minima are complement of each other.
Maxima and Minima of a function of one variables
If f(x) is a single valued function defined in a region R then
Maxima is a maximum point 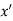 if and only if
if and only if 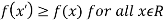
Minima is a minimum point 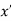 if and only if
if and only if 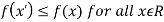


Maxima and Minima of a function of two independent variables
Let 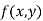 be a defined function of two independent variables.
be a defined function of two independent variables.
Then the point 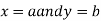 is said to be a maximum point of
is said to be a maximum point of  if
if
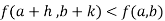
Or 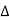 =
= 
For all positive and negative values of h and k.
Similarly the point 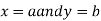 is said to be a minimum point of
is said to be a minimum point of 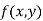 if
if
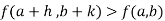
Or 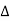 =
= 
For all positive and negative values of h and k.
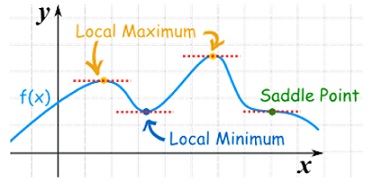
Saddle point:
Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point.
Note-
Increasing and decreasing functions-
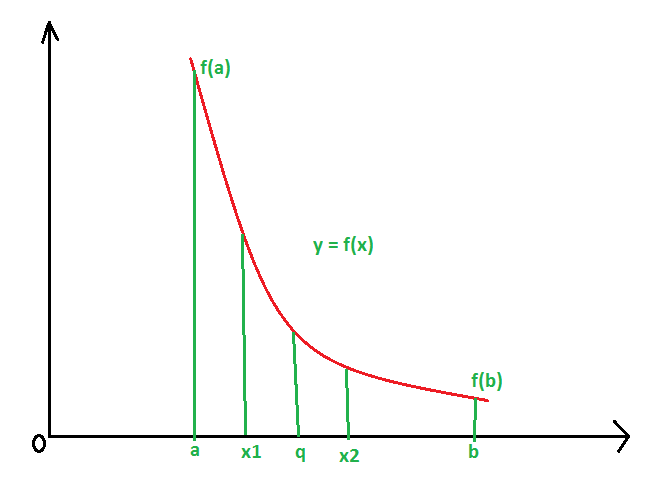
A function is said to be increasing function in an interval [a, b] if y increases as well as x increases from a to b.
Or in other words, A function is said to be an increasing function in [a, b] if its first derivative is greater than zero for all values of x in an interval [a, b].
And
A function is said to be decreasing function in an interval [a, b] if y decreases as well as x increases from a to b.
“If the first derivative is less than zero for all values of x in an interval [a, b] then the function y = f(x) is a decreasing function in [a, b].
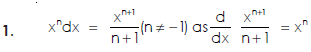
Criteria for maximum and minimum-
For a function y = f(x) to attain a maximum point at x = a,
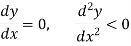
For minimum point-

Conditions for maximum and minimum-
Necessary Condition-
If a function f(x) is maximum or minimum at a point x = b and if f’(b) exists then f’ (b) = 0.
Sufficient Condition-
If b is a point in an interval where f(x) is defined and if f ‘(b) = 0 and f’’(b) 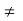 0, then f(b) is maximum if f’’(b) < 0 and is minimum if f’’(b) > 0. (The proof is not shown at present).
0, then f(b) is maximum if f’’(b) < 0 and is minimum if f’’(b) > 0. (The proof is not shown at present).
Working Rule:
First derivative method
To find the maximum or minimum point of a curve y = f(x).
Find f ‘(x) and equate it to zero. From the equation f ‘(x) = 0, find the value of x, say a and b.
Here the number of roots of f ‘(x) = 0 will be equal to the number of degree of f ‘(x) = 0.
Then find f ‘(a – h) and f ‘(a + h), then note the change of sign if any (here h is very small).
If the change is from positive to negative, f(x) will be maximum at x = a. If again the change of sign is from negative to positive, f(x) will be maximum at x = a.
Similarly for x = b.
Second derivative method-
First we find the first derivative of y = f(x) i.e dy/dx and make it zero.
From the equation 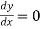 find the value of x say a and b.
find the value of x say a and b.
The again we find the second derivative of y or 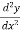 .
.
Put x = a in 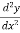 , if
, if 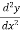 at x = a is negative then the function is maximum at x = a and maximum value will be f(a).
at x = a is negative then the function is maximum at x = a and maximum value will be f(a).
If the value of 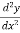 at x = a is positive, then the function is minimum and the minimum value will be f(a)
at x = a is positive, then the function is minimum and the minimum value will be f(a)
Similarly we take for x = b.
Example: Examine for maximum and minimum for the function f(x) = 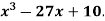
Sol.
Here the first derivative is-
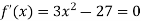
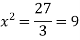
So that, we get-
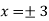
Now we will get to know that the function is maximum or minimum at these values of x.
For x = 3
Let us assign to x, the values of 3 – h and 3 + h (here h is very small) and put these values at f(x).
Then-
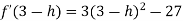 Which is negative for h is very small
Which is negative for h is very small
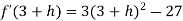 Which is positive
Which is positive
Thus f’(x) changes sign from negative to positive as it passes through x = 3.
So that f(x) is minimum at x = 3 and the minimum value is-
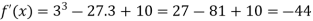
And f(x) is maximum at x = -3.
Example: Find out the value of x for which the function f(x) =  is minimum of maximum.
is minimum of maximum.
Sol.
Let
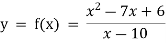
Then the first derivative will be-
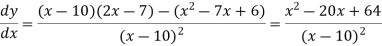
Putting 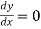 , we get-
, we get-
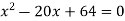
By using middle term splitting-
We get-
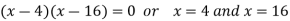
Now we will find the second derivative-
We get-

Here
At x = 4, 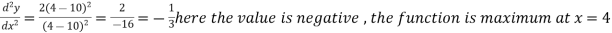
At x = 16, 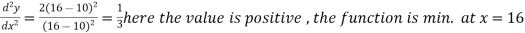
Example: Find all points of maxima and minima of the function f(x) =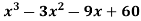 .
.
Sol.
Here,
f(x) =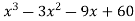 .
.
f’(x) =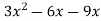
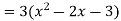
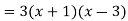
Put, f’(x) = 0
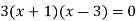
We get,

Hence x = -1 and x = 3 are the critical values of the given function.
Now take,
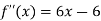
Where x = -1, then f’’(x) = -12
Since f’’(x) < 0 at x = -1, the function has maxima at x = -1
And when x = 3, then f’’(x) = 12
Since f’’(x) > 12 at x = 3, the function has minima at x =
Key takeaways-

For minimum point-
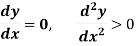
3. Necessary Condition- If a function f(x) is maximum or minimum at a point x = b and if f’(b) exists then f’ (b) = 0.
Sufficient Condition- If b is a point in an interval where f(x) is defined and if f ‘(b) = 0 and f’’(b) 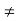 0, then f(b) is maximum if f’’(b) <0 and is minimum if f’’(b) > 0. (The proof is not shown at present).
0, then f(b) is maximum if f’’(b) <0 and is minimum if f’’(b) > 0. (The proof is not shown at present).
Introduction (Integration)-
Integration is the reverse process of differentiation. It is also called annti-differentiation.
Integration calculus has its own application in economics, Engineering, Physics, Chemistry, business, commerce, etc.
The integral of a function is denoted by the sign 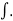
Let the function is y = f(x),
Its derivative is-
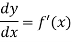
Then
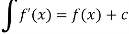
Where c is the arbitrary constant.
For example,
A function,
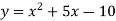
Then, its derivative-
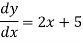
Or
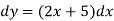
Then-

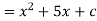
Here c is an arbitrary constant.
Some fundamental integrals-
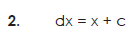
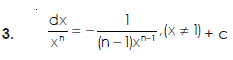
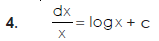
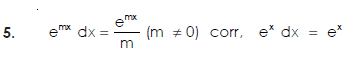
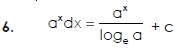
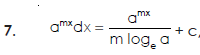
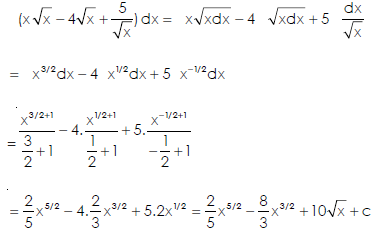
Methods of integration-
Simple integration-
Some standard form of simple integration-
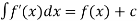


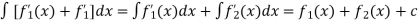
The integration of 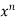 will be as follows-
will be as follows-
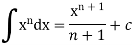
Example: Find the integral of- 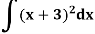
Sol.
We know that-
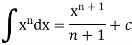
Then
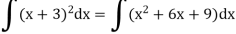
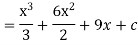

Example: Find the integral

Sol.
We know that-

Then
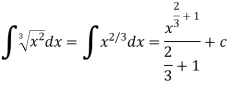
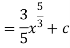
Example: Evaluate-
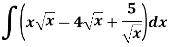
Sol.
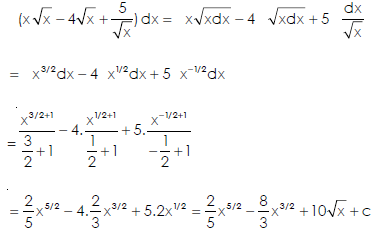
Integration by substitution-
Example: Evaluate the following integral-

Sol.
Let us suppose,

Then-

Or

Substituting –
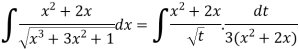

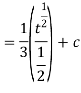
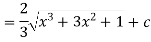
Logarithmic function-
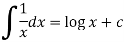
Example: Evaluate the following integral-
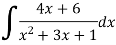
Sol.
Let us suppose-
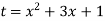
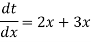
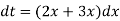
Now
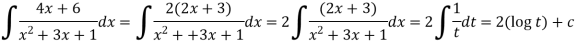
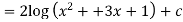
Integration of exponential function-
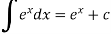
Example: Evaluate-
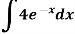
Sol.
Let,

Now substituting-

Integration of product of two functions-
Suppose we have two function say- f(x) and g(x), then
The integral of product of these two functions is-

Note-
We chose the first function as method of ILATE-
Which is-
I – Inverse trigonometric function
L – Log function
A – Algebraic function
T- Trigonometric function
E- Exponential function
Example: Evaluate-
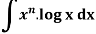
Sol.
Here according to ILATE,
First function = log x
Second function = 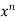
We know that-
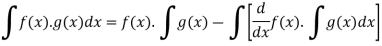
Then-
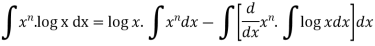
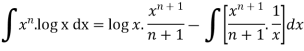
On solving, we get-
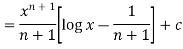
References-