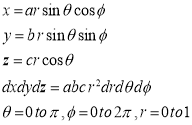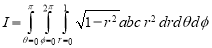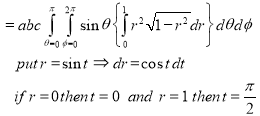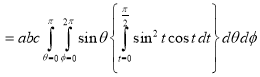UNIT 4
MULTIVARIABLE CALCULUS (INTEGRATION)
Double integral –
Before studying about multiple integrals, first let’s go through the definition of definition of definite integrals for function of single variable.
As we know, the integral
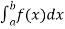
Where is belongs to the limit a ≤ x ≤ b
This integral can be written as follows-
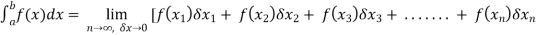
Now suppose we have a function f(x , y) of two variables x and y in two dimensional finite region R in xy-plane.
Then the double integration over region R can be evaluated by two successive integration

Evaluation of double integrals-
If A is described as 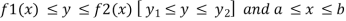
Then,
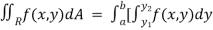 ]dx
]dx
Let do some examples to understand more about double integration-
Example-1: Evaluate 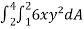 , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
Sol. Let , I = 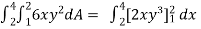
= 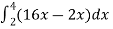
= 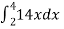
= 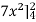
= 84 sq. Unit.
Which is the required area.
Example-2: Evaluate 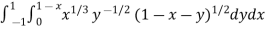
Sol. Let us suppose the integral is I,
I = 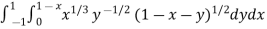
Put c = 1 – x in I, we get
I = 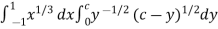
Suppose, y = ct
Then dy = c
Now we get,
I = 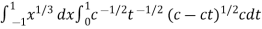
I = 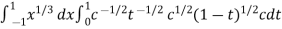
I = 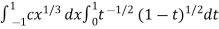
I = 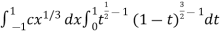
I = 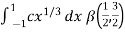
As we know that by beta function,
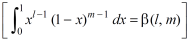
Which gives,
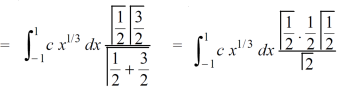
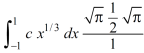
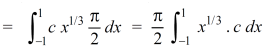
Now put the value of c, we get
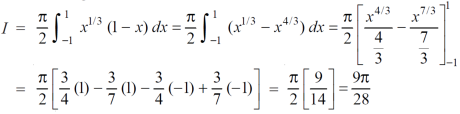
Example-3: Evaluate the following double integral,
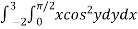
Sol. Let,
I = 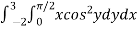
On solving the integral, we get
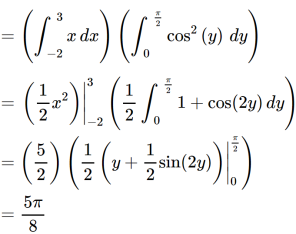
Double Integral over Rectangular and general regions
Consider a function f (x, y) defined in the finite region R of the x-y plane. Divide R into n elementary areas A1, A2,…,An. Let (xr, yr) be any point within the rth elementary are Ar
Fig. 6.1
f (x, y) dA = f (xr, yr) A
Evaluation of Double Integral when limits of Integration are given (Cartesian Form).
Ex. 1: Evaluate 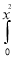 ey/x dy dx.
ey/x dy dx.
Soln.:
Given: I = 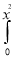 ey/x dy dx
ey/x dy dx
Here limits of inner integral are functions of y therefore integrate w.r.t y,
I = 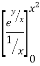
 dx
dx
= 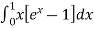
= 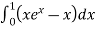
I = 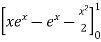
= =
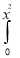 ey/x dy dx =
ey/x dy dx =
Ex. 2: Evaluate x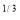 y
y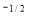 (1 – x –y)
(1 – x –y)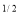 dx dy.
dx dy.
Soln.:
Given: I = x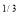 y
y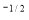 (1 – x –y)
(1 – x –y)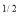 dx dy.
dx dy.
Here the limits of inner integration are functions of y therefore first integrate w.r.t y.
I = x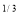 dx
dx 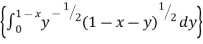
Put 1 – x = a (constant for inner integral)
I = x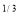 dx
dx 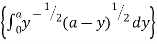
Put y = at dy = a dt
y | 0 | a |
t | 0 | 1 |
I = x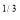 dx
dx 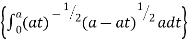
I = x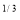 dx
dx 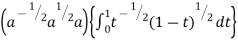
I = x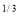 a dx
a dx
I = x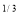 (1 – x) dx = (x
(1 – x) dx = (x – x4/3) dx
– x4/3) dx
I = 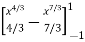
=
I = =
x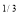 y
y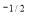 (1 – x –y)
(1 – x –y)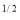 dx dy =
dx dy =
Ex. 3 : Evaluate 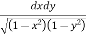
Soln. :
Let, I = 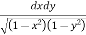
Here limits for both x and y are constants, the integral can be evaluated first w.r.t any of the variables x or y.
I = dy 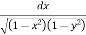
I = 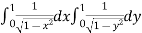
= 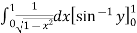
= 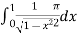
= 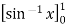
=
= 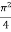
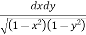 =
=
Ex. 4: Evaluate e–x2 (1 + y2) x dx dy.
Soln. :
Let I = e–x2 (1 + y2) x dy = dy e–x2 (1 + y2) x dy
= dy e– x2 (1 + y2)  dx
dx
= dy [∵ f (x) ef(x) dx = ef(x) ]
= (–1) dy (∵ e– = 0)
= = =
e–x2 (1 + y2) xdx dy =
NOTES:
Type II: Evaluation of Double Integral when region of Integration is provided (Cartesian form)
Ex.1: Evaluate y dx dy over the area bounded by x= 0 y = 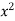 and x + y = 2 in the first quadrant
and x + y = 2 in the first quadrant
Soln. :
The area bounded by y = x2 (parabola) and x + y = 2 is as shown in Fig.6.2
The point of intersection of y = x2 and x + y = 2.
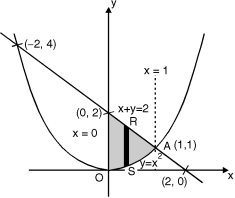
x + x2 = 2 x2 + x – 2 = 0
x = 1, – 2
At x = 1, y = 1 and at x = –2, y = 4
Fig. 6.2
(1, 1) is the point of intersection in Ist quadrant. Take a vertical strip SR, Along SR x constant and y varies from S to R i.e. y = x2 to y = 2 – x.
Now slide strip SR, keeping IIel to y-axis, therefore y constant and x varies from x = 0 to x = 1.
I = 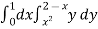
= 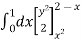
= 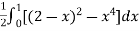
= (4 – 4x + 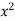 –
– 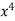 ) dx
) dx
= =
I = 16/15
Ex. 2 : Evaluate 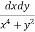 over x 1, y
over x 1, y 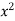
Soln. :
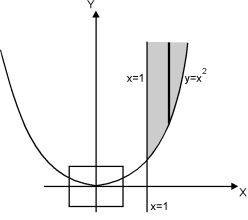 Let I =
Let I = 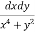 over x 1, y
over x 1, y 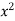
The region bounded by x 1 and y 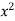
Is as shown in Fig. 6.3.
Fig. 6.3
Take a vertical strip along strip x constant and y varies from y = 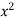
To y = . Now slide strip throughout region keeping parallel to y-axis. Therefore y constant and x varies from x = 1 to x = .
I = 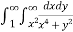
= 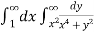
= 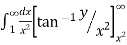 [ ∵
[ ∵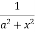 dx = tan–1 (x/a)]
dx = tan–1 (x/a)]
= 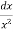 =
=
= – = (0 – 1)
I =
Ex. 3 : Evaluate (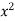 +
+ 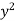 ) dx dy through the area enclosed by the curves y = 4x, x + y = 3 and y =0, y = 2.
) dx dy through the area enclosed by the curves y = 4x, x + y = 3 and y =0, y = 2.
Soln. :
Let I = (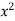 +
+ 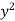 ) dx dy
) dx dy
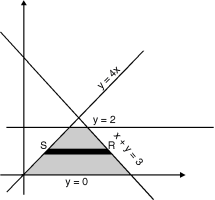 The area enclosed by the curves y = 4x, x + y =3, y = 0 and y = 2 is as shown in Fig. 6.4.
The area enclosed by the curves y = 4x, x + y =3, y = 0 and y = 2 is as shown in Fig. 6.4.
(find the point of intersection of x + y = 3 and y = 4x)
Fig. 6.4
Take a horizontal strip SR, along SR y constant and x varies from x = to x = 3 – y. Now slide strip keeping IIel to x axis therefore x constant and y varies from y = 0 to y = 2.
I = dy (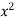 +
+ 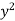 ) dx
) dx
= 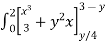
= 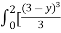 +
+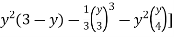 dy
dy
I = 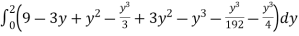
= 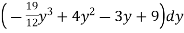
= 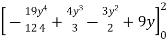
= + – 6 + 18
I =
Ex. 1 : Change the order of integration for the integral 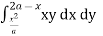 and evaluate the same with reversed order of integration.
and evaluate the same with reversed order of integration.
Soln. :
Given, I = 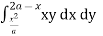 …(1)
…(1)
 In the given integration, limits are
In the given integration, limits are
y = 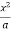 , y = 2a – x and x = 0, x = a
, y = 2a – x and x = 0, x = a
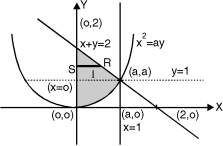
The region bounded by x2 = ay, x + y = 2a Fig.6.5
And x = 0, x = a is as shown in Fig. 6.5
Here we have to change order of Integration. Given the strip is vertical.
Now take horizontal strip SR.
To take total region, Divide region into two parts by taking line y = a.
1 st Region :
Along strip, y constant and x varies from x = 0 to x = 2a – y. Slide strip IIel to x-axis therefore y varies from y = a to y = 2a.
I1 = dy xy dx …(2)
2nd Region :
Along strip, y constant and x varies from x = 0 to x = . Slide strip IIel to x-axis therefore x-varies from y = 0 to y = a.
I2 = dy xy dx …(3)
From Equation (1), (2) and (3),
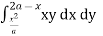 = dy xy dx + dy xy dx
= dy xy dx + dy xy dx
= 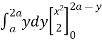 + y dy
+ y dy 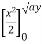
=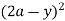 dy + (ay) dy = y (4a2 – 4ay + y2) dy + ay2 dy
dy + (ay) dy = y (4a2 – 4ay + y2) dy + ay2 dy
= (4a2 y – 4ay2 + y3) dy + y2 dy
= 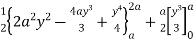
= 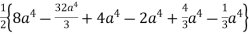 +
+ 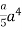
= a4
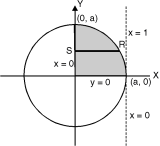 Ex. 2 : Evaluate
Ex. 2 : Evaluate
I = 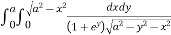
Soln. :
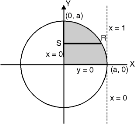 Given : I =
Given : I = 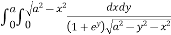 …(1)
…(1)
In the given integration, limits are
x = 0, x = a, y = 0, y = 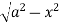
The bounded region is as shown in Fig. **.
In the given, strip is vertical. Now take horizontal strip SR. Along strip y constant and x varies from x = 0 to
x = 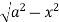 . Slide strip IIel to X-axis therefore y varies from y = 0 to y = a.
. Slide strip IIel to X-axis therefore y varies from y = 0 to y = a.
I = dy 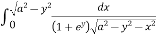
= 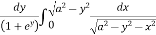
Put a2 – y2 = b2
I = 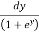
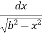
= 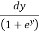 =
= 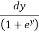
= 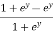 dy =
dy = 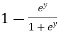 dy
dy
= 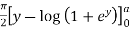
=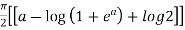
= 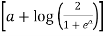
= 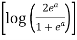 [∵ a = a loge]
[∵ a = a loge]
I = dy 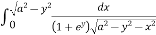 =
= 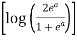
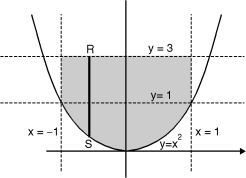 Ex.3 : Express as single integral and evaluate dy dx + dy dx.
Ex.3 : Express as single integral and evaluate dy dx + dy dx.
Soln. :
Given : I = dy dx + dy dx
I = I1 + I2
The limits of region of integration I1 are
x = – ; x = and y = 0, y = 1 and I2 are x = – 1,
x = 1 and y = 1, y = 3.
The region of integration are as shown in Fig. 6.7
To consider the complete region take a vertical strip SR along the strip y varies from y = x2 to
y = 3 and x varies from x = –1 to x = 1. Fig. 6.7
I = 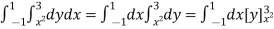
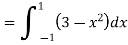
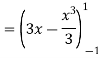
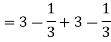
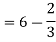
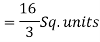
Evaluation of Double Integral by Changing Cartesian to Polar co-ordinates (when limits are given).
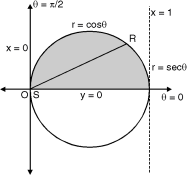 Ex. 1 : Evaluate
Ex. 1 : Evaluate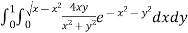
Soln. :
The region of integration bounded by
y = 0, y = 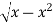 and x = 0, x = 1
and x = 0, x = 1
y = 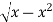 x2 + y2 = x
x2 + y2 = x
The region bounded by these is as shown in Fig. 6.8.
Convert the integration in polar co-ordinates by using x = r cos , y = r sin and dx dy = r dr d
x2 + y2 = x becomes r = cos
y = 0 becomes r sin = 0 = 0
x = 0 becomes r cos = 0 =
And x = 1 becomes r = sec
Take a radial strip SR with angular thickness , Along strip constant and r varies from r = 0 to r = cos . Turning strip throughout region therefore varies from = 0 to =
I = 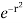 r dr d
r dr d
= 4 cos sin d r 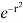 dr
dr
= 4 cos sin d [–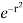 ]
]
= – 2 cos sin [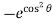 +1] d
+1] d
= – 2 [cos sin 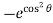 – cos sin ] d
– cos sin ] d
= –2 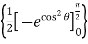 + 2 cos sin d
+ 2 cos sin d
= – + 2
= + 1 =
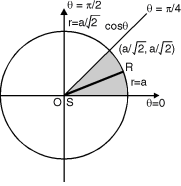 Ex. 2: Sketch the area of double integration and evaluate
Ex. 2: Sketch the area of double integration and evaluate
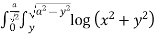 dxdy
dxdy
Soln. :
Let I = 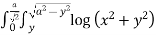 dxdy
dxdy
The region of integration is bounded by the curves
x = y, x = 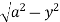 and y = 0, y = Fig. 6.9
and y = 0, y = Fig. 6.9
i.e. x = y, x2 + y2 = a2 and y = 0, y =
The region bounded by these is as shown in Fig. 6.9.
The point of intersection of x = y and x2 + y2 = a2 is x =
Convert given integration in polar co-ordinates by using polar transformation x = r cos , y = r sin and dx dy = r dr d
x = y gives r cos = r sin tan = 1 =
x2 + y2 = a2 r2 = a2 r = a
y = 0 gives r sin = 0 = 0.
y = gives r sin = r = cosec
Take a radial strip SR, along SR constant and r varies from r = 0 to r = a. Turning this strip throughout region therefore varies from = 0 to =
I = log r2 r dr d = 2 d r log r dr
I = 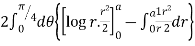
= 2 d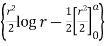
= 2 d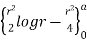
= 2 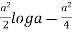 d
d
= 2 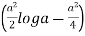 []
[]
I = 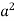 [/4] =
[/4] = 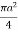
Evaluation of Double Integral when region of Integration is provided (Polar form)
Ex. 1 : Evaluate r4 cos3 dr d over the interior of the circle r = 2a cos
Soln. :
The region of the integration is as shown in Fig. 6.10.Take a radial strip SR, along strip constant and r varies from r = 0 to r = 2a cos. Now turning this strip throughout region therefore varies from = to =
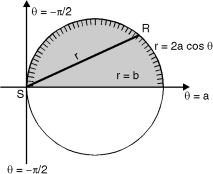 I = r4 cos3 dr d
I = r4 cos3 dr d
= cos3 d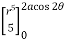
= 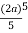 cos3 cos5 d
cos3 cos5 d
= 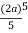 cos8 d Fig. 6.10
cos8 d Fig. 6.10
= 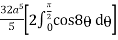
= 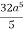 2
2
I = 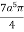
r4 cos3 dr d = 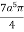
Ex. 2 : Evaluate r sin dr d over the cardioid r = a (1 – cos ) above the initial line.
Soln. :
The cardioid r = a (1 – cos ) is as shown in Fig. 6.11. The region of the integration is above the initial line.
Take a radial strip SR, along strip constant and r Varies from r = 0 to r = a (1 – cos ).
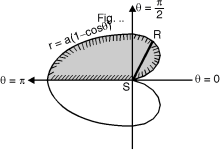 New turning the strip throughout region therefore varies from = 0 to = .
New turning the strip throughout region therefore varies from = 0 to = .
I = r sin dr d
= sin d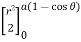
Fig.6.11
= sin [a2 (1 – cos )2]
= 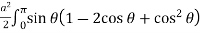
I = 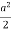 (sin – 2 sin cos + sin
(sin – 2 sin cos + sin 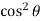 ) d
) d
= 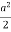 2 (sin – sin2 + sin
2 (sin – sin2 + sin 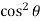 ) d
) d
= 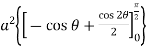 +
+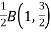
I = a2= a2
I = 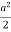
NOTES:


 Area enclosed by plane curves expressed in Cartesian coordinates:
Area enclosed by plane curves expressed in Cartesian coordinates:


 Y (x,y) P Q (x+dx,y+dy) y=f(x)
Y (x,y) P Q (x+dx,y+dy) y=f(x)


 V U
V U
G H dxdy
 A R S B
A R S B
x=a y=0 x=b X
Consider the area enclosed by the curves 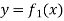
And 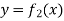 and the ordinates
and the ordinates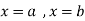
Area =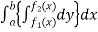
Consider the area enclosed by the curves 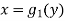
And 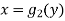 and the ordinates
and the ordinates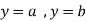
Area =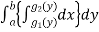
Area enclosed by plane curves expressed in Polar coordinates:
Consider the area enclosed by the polar curves 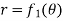
And 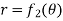 and the line
and the line 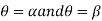
Area =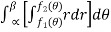
Ex.1: Find the area between the curves 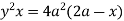 and its asymptote.
and its asymptote.
Solution: The curve is symmetrical about x axis not passing through origin. Also 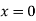 is the asymptote to the curve and intersect x axis at
is the asymptote to the curve and intersect x axis at 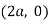 for
for 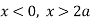 curve doesn’t exists. And for
curve doesn’t exists. And for 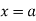 and
and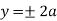 . Because of symmetry
. Because of symmetry
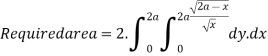
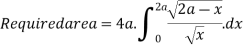
Put 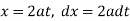
x | 0 | 2a |
t | 0 | 1 |
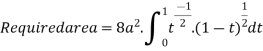
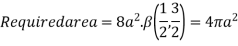
Ex: 2: Show that the area of curve 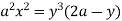 is
is 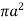
Solution: The curve is symmetrical about Y - axis passing through origin and there exists a cusp at origin. It intersects Y-axis at (0 , 0) , (0 , 2a) .
Also 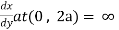 .
.
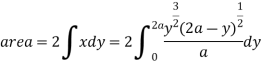
Putting 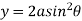
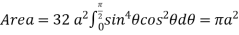 .
.
Ex.3: Find the Area included between the two cardioids 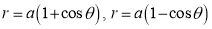
Solution: - Area = 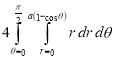
= 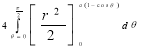
= 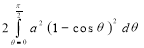
= 
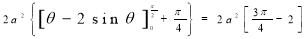
Ex.4: Find the Area common to the two circle 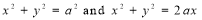
Solution: - By converting the given circle into polar form we get
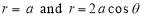
Area = 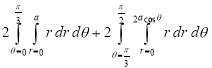
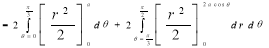
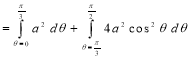
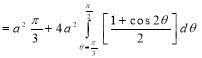
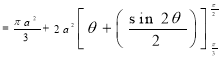
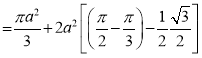
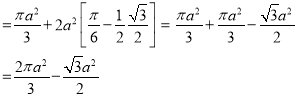
Definition: Let f(x,y,z) be a function which is continuous at every point of the finite region (Volume V) of three dimensional space. Divide the region V into n sub regions of respective volumes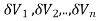 . Let (
. Let (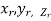 ) be a point in the
) be a point in the 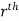 sub region then the sum:
sub region then the sum:
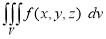 =
= 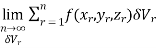
Is called triple integration of f(x, y, z) over the region V provided limit on R.H.S of above Equation exists.
Spherical Polar Coordinates
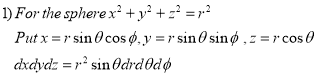
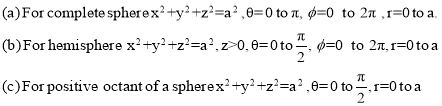
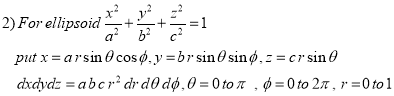

Where the integral is extended to all positive values of the variables subjected to the condition 
Ex.1: Evaluate
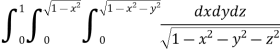
Solution : Let
I = 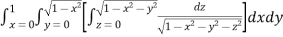
= 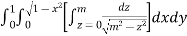
(Assuming m = 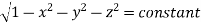 )
)
= 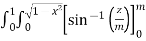 dxdy
dxdy
= 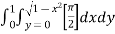
=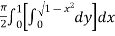
= 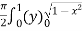 dx
dx
= 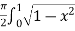 dx
dx
= 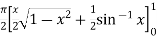
=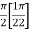
I =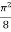
Ex.2: Evaluate 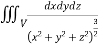 Where V is annulus between the spheres
Where V is annulus between the spheres 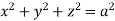
And 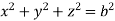 (
(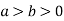 )
)
Solution: It is convenient to transform the triple integral into spherical polar co-ordinate by putting
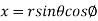 ,
, 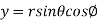 ,
, 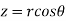
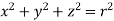 , dxdydz=
, dxdydz=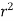 sin
sin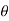 drd
drd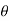 d
d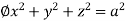 ,
,
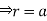 and
and 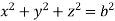
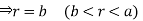
For the positive octant, r varies from r =b to r =a , 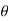 varies from
varies from 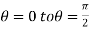
And 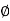 varies from
varies from 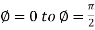
I= 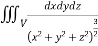
= 8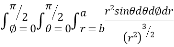
=8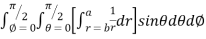
=8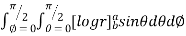
=8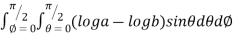
=8 log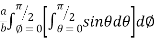
= 8 log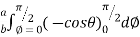
I= 8 log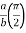 I = 4 log
I = 4 log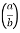
Ex.3: Evaluate 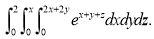
Solution:-
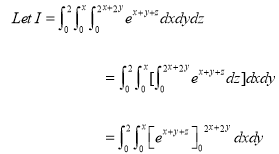
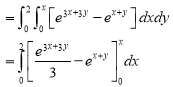
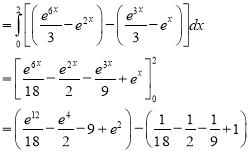
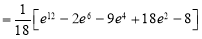
Ex.4:Evaluate 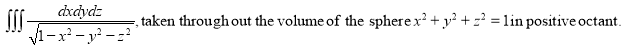
Solution:- 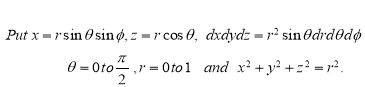
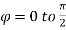
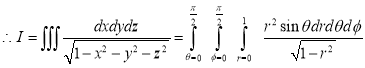
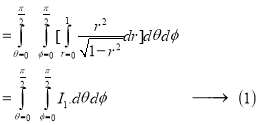
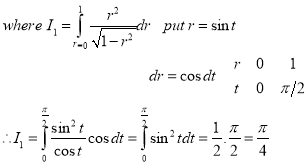
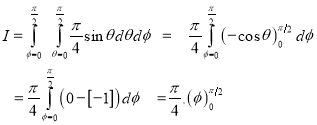
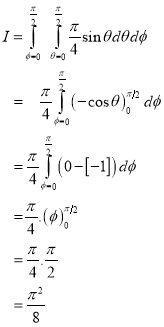
NOTES:
The volume of solid is given by
Volume =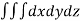
In Spherical polar system
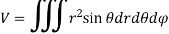
In cylindrical polar system
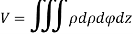
Ex.1: Find Volume of the tetrahedron bounded by the co-ordinates planes and the plane
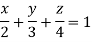
Solution: Volume =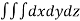 ………. (1)
………. (1)
Put 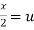 ,
, 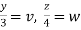
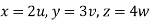
From equation (1) we have
V = 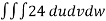
=24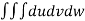
=24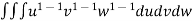 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 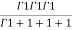
=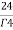 =
=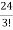 = 4
= 4
Volume =4
Ex.2: Find volume common to the cylinders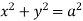 ,
, 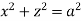 .
.
Solution: For given cylinders,
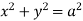 ,
, 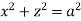 .
.
Z varies from
Z=-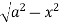 to z =
to z = 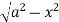
Y varies from
y= -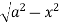 to y =
to y = 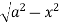
x varies from x= -a to x = a
By symmetry,
Required volume= 8 (volume in the first octant)
=8 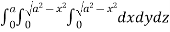
=8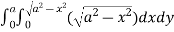
= 8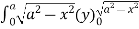 dx
dx
=8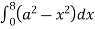
=8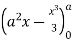
=8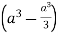
Volume = 16
Ex.3: Evaluate
1. 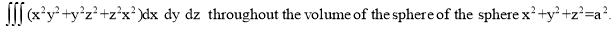 Solution:-
Solution:-
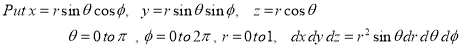
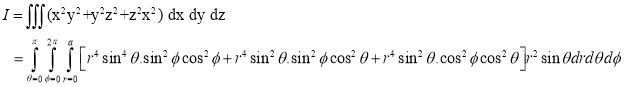
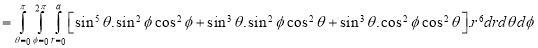
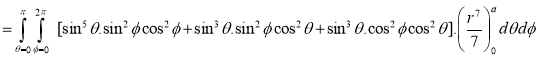
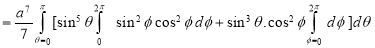
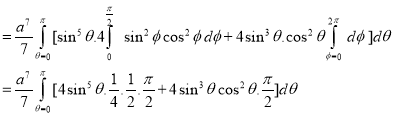
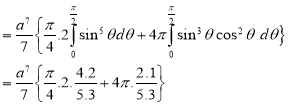
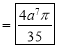
Ex.4: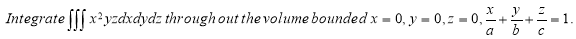
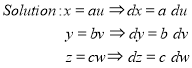
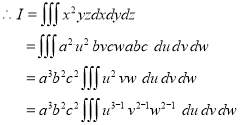
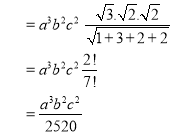
Ex.5: Evaluate 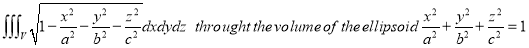
Solution:- Put