UNIT 2
CALCULUS OF ONE VARIABLE
Important definitions-
Continuity- suppose that a function f(x) is defined in the interval I , then it is said to be continuous at x=a , if
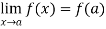
Differentiability- A function f(x) is said to be differentiable at x=a if
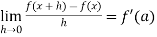 exists where ‘a’ belongs to I
exists where ‘a’ belongs to I
Rolle’s theorem-
Suppose f(x) is a function defined on [a , b] and it satisfies the following conditions
1. f(x) is continuous in [a , b]
2. f(x) is differentiable in (a , b)
3. f(a) = f(b)
Then there exists atleast a point point c ϵ (a , b) , where a<b , such that f’(c) = 0
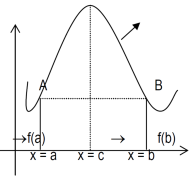
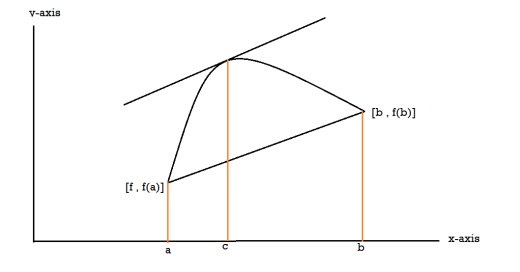
Proof: suppose y = f(x) is a function and A(a , f(a)) , B(b , f(b)) be two points on the curve f(x) and a,b are two end points. Now conditions for Rolle’s theorem-
1.f(x) is a continuous function in[a , b] , from the figure without breaks in between A&B on y = f(x).
2. f(x) is differentiable in (a , b), because joining A and B we get a line AB.
Slope of the line AB=0 then a point C at P also a tangent at P, or Q,R,S is parallel to x –axis.
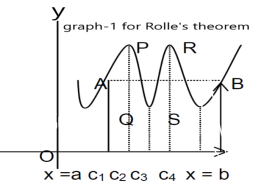
Slope of the tangent at P or Q,R,S , will be 0 ,even the curve y = f(x) decreases or increases, that means f(x) is constant.
Derivative of f(x),
f’(c) = 0
That’s why, f’(c) = 0
3. The slope of the line AB is equal to zero, that means the line AB is parallel to x-axis.
So that, f(a) = f(b)
Example 1
Verify Rolle’s theorem for the function f(x) = x2 for 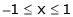
Solution:
Here f(x) = x2; 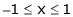
i) Since f(x) is algebraic polynomial which is continuous in [-1, 1]
Ii) Consider f(x) = x2
Diff. w.r.t. x we get
f'(x) = 2x
Clearly f’(x) exists in (-1, 1) and does not becomes infinite.
Iii) Clearly
f(-1) = (-1)2 = 1
f(1) = (1)2 = 1
 f(-1) = f(1).
f(-1) = f(1).
Hence by Rolle’s theorem, there exist 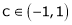 such that
such that
f’(c) = 0
i.e. 2c = 0
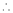 c = 0
c = 0
Thus 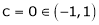 such that
such that
f'(c) = 0
Hence Rolle’s Theorem is verified.
Example 2 Verify Rolle’s Theorem for the function f(x) = ex(sin x – cos x) in
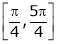
Solution:
Here f(x) = ex(sin x – cos x); 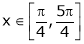
i) Ex is an exponential function continuous for every 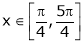 also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in
also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in 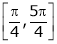 and Hence ex(sin x – cos x) is continuous in
and Hence ex(sin x – cos x) is continuous in 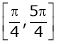 .
.
Ii) Consider
f(x) = ex(sin x – cos x)
Diff. w.r.t. x we get
f’(x) = ex(cos x + sin x) + ex(sin x + cos x)
= ex[2sin x]
Clearly f’(x) is exist for each 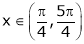 & f’(x) is not infinite.
& f’(x) is not infinite.
Hence f(x) is differentiable in 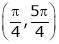 .
.
Iii) Consider
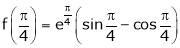
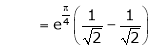
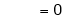
Also,
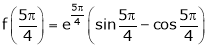
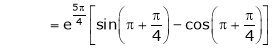
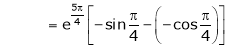
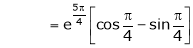
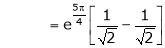

Thus 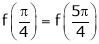
Hence all the conditions of Rolle’s theorem are satisfied, so there exist 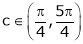 such, that
such, that
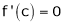
i.e. 
i.e. sin c = 0

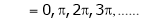
But
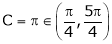
Hence Rolle’s theorem is verified.
Example-3
Verify whether Rolle’s theorem is applicable or not for
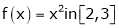
Solution:
Here f(x) = x2; 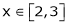
i) X2 is an algebraic polynomial hence it is continuous in [2, 3]
Ii) Consider
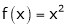
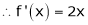
F’(x) exists for each 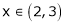
Iii) Consider
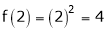
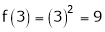
Thus 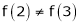 .
.
Thus all conditions of Rolle’s theorem are not satisfied Hence Rolle’s theorem is not applicable for f(x) = x2 in [2, 3]
Example-4:
Example: Verify Rolle’s theorem for the given functions below-
1. f(x) = x³ - 6x²+11x-6 in the interval [1,3]
2. f(x) = x²-4x+8 in the interval [1,3]
Sol. (1)
As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = f(3) = 0
Now we find f’(x) = 0
3x² - 12x +11 = 0
We get, x = 2+ 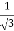 and 2 -
and 2 - 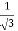
Hence both of them lie in (1,3).
Hence the theorem holds good for the given function in interval [1,3]
(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5
Hence f(1) = f(3)
Now the first derivative of the function,
f’(x) = 0
2x – 4 = 0 , gives
X = 2
We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.
This means that the Rolle’s theorem holds good for the given function and given interval.
Lagrange’s Mean value Theorem:-
Suppose that f(x) be a function of x such that,
1. If it is continuous in [a , b]
2. If it is differentiable in (a , b)
Then there atleast exists a value cϵ (a , b)
f’(c) = 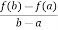
Proof:
Lets define a function g(x),
g(x) = f(x) – Ax ………………..(1)
Here A is a constant which is to be determined,
So that, g(a) = g(b)
Now,
g(a) = f(a) – Aa
g(b) = f(b) – Ab
So,
g(a) = g(b),
f(a) – Aa = f(b) – Ab ,
Which gives,
A = 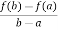 …………………..(2)
…………………..(2)
As right hand side of eq.(1) is continuous in [a,b] , so that g(x) is continuous.
And right hand side of eq.(1) is differential in (a,b) , so that g(x) is differentiable in (a,b).
And g(a) = g(b) , because of the choice of A.
Hence g(x) satisfies all the conditions of Rolle’s theorem.
So that,
There exists a value c such that a<c<b at which g’(c) = 0
Now, differentiate eq. (1) with respect to x, we get
g’(x) = f’(x) – A
Here we know that, x = c,
g’(c) = f’(c) – A
As g’(c) = 0, then
f’(c) – A =0
So that,, f’(c) = A,
From equation (2) , we get
f’(c) = 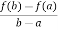 hence proved.
hence proved.
Example-1:
Verify the Lagrange’s mean value theorem for
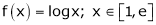
Solution:
Here 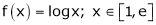
i) Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]
Ii) Consider f(x) = log x.
Diff. w.r.t. x we get,
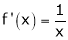
Clearly f’(x) exists for each value of 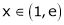 & is finite.
& is finite.
Hence all conditions of LMVT are satisfied Hence at least 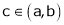
Such that
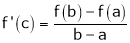
i.e. 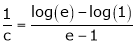
i.e. 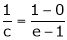
i.e. 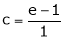
i.e. 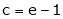
Since e = 2.7183
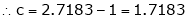
Clearly c = 1.7183 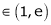
Hence LMVT is verified.
Example-2:
Verify mean value theorem for f(x) = tan-1x in [0, 1]
Solution:
Here 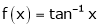 ;
; 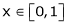
i) Clearly 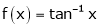 is an inverse trigonometric function and hence it is continuous in [0, 1]
is an inverse trigonometric function and hence it is continuous in [0, 1]
Ii) Consider 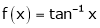
Diff. w.r.t. x we get,
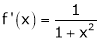
Clearly f’(x) is continuous and differentiable in (0, 1) & is finite
Hence all conditions of LMVT are satisfied, Thus there exist 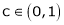
Such that
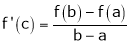
i.e. 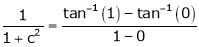
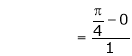
i.e. 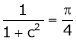
i.e. 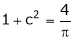
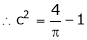
i.e. 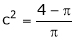
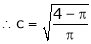
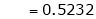
Clearly 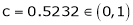
Hence LMVT is verified.
Example-4;
Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].
Sol. As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).
f(x) = (x-1)(x-2)(x-3)
f(x) = x-6x²+11x-6
Now at x = 0, we get
f(0) = -6 and
At x = 4, we get.
f(4) = 6
Diff. The function w.r.t.x , we get
f’(x) = 3x²-6x+11
Suppose x = c, we get
f’(c) = 3c²-6c+11
By Lagrange’s mean value theorem,
f’(c) = 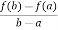 =
= 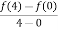 =
= 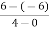 = 3
= 3
Now we get,
3c²-6c+11 = 3
3c²-6c+8 = 0
On solving the quadratic equation, we get
C = 2 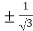
Here we see that the value of c lies between 0 and 4
Therefore the given function is verified.
Meaning of sign of Derivative:
Let f(x) satisfied LMVT in [a, b]
Let x1 and x2 be any two points laying (a, b) such that x1< x2
Hence by LMVT, 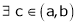 such that
such that 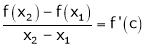
i.e. 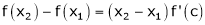 … (1)
… (1)
Cast I:
If 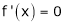
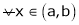 then
then 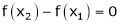
i.e. 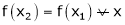
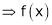 is constant function
is constant function
Case II:
If 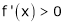
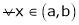 then from equation (1)
then from equation (1)
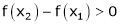
i.e. 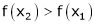
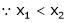 means x2 - x1> 0 and
means x2 - x1> 0 and 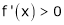
Thus for x2> x1
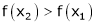
Thus f(x) is increasing function is (a, b)
Case III:
If 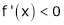
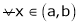
Then from equation (1)
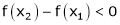
i.e. 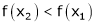
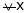
Since 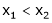 and
and 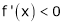 then
then 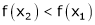
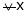 hence f(x) is strictly decreasing function.
hence f(x) is strictly decreasing function.
Example-5:
Prove that
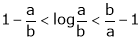
And hence show that
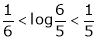
Solution:
Let
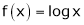 ;
; 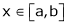
i) Clearly 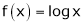 is a logarithmic function and hence it is continuous also
is a logarithmic function and hence it is continuous also
Ii) Consider 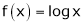
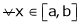
Diff. w.r.t. x we get,
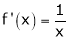
Clearly f’(x) exist and finite in (a, b) Hence f(x) is continuous and differentiable in (a, b). Hence by LMVT 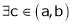
Such that
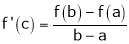
i.e. 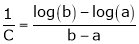
i.e. 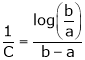
Since
a < c < b
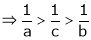
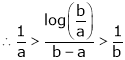
i.e. 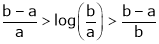
i.e. 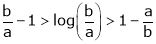
i.e. 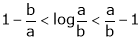
i.e. 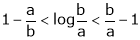
Hence the result
Now put a = 5, b = 6 we get
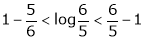
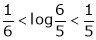
Hence the result
Example-6:
Prove that 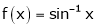 ,
, 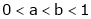 use mean value theorem to prove that,
use mean value theorem to prove that,
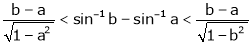
Hence show that
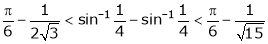
Solution:
i) Let f(x) = sin-1x; 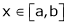
Ii) Clearly f(x) is inverse trigonometric function and hence it is continuous in [a, b]
Iii) Consider f(x) = sin-1x
Diff. w.r.t. x we get,
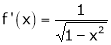
Clearly f’(x) is finite and exists for 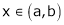 . Hence by LMVT,
. Hence by LMVT, 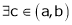 such that
such that
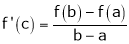
i.e. 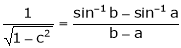
Since a < c < b
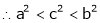
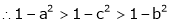
i.e. 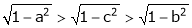
i.e. 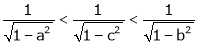
i.e. 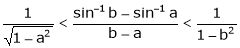
i.e. 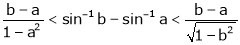
Hence the result
Put 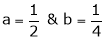 we get
we get
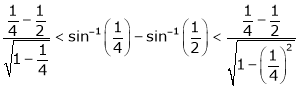
i.e. 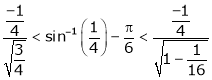
i.e. 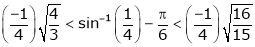
i.e. 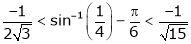
i.e. 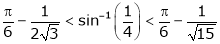
Hence the result
Cauchy’s Mean Value Theorem:
Suppose we have two functions f(x) and g(x) of x, such that,
1. Both functions are continuous in [a,b]
2. Both functions are differentiable in (a,b)
3. g’(x) ≠ 0 for any x ϵ (a,b)
These three exists atleast , x = c ϵ (a,b) , at which
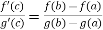
Proof: suppose ,we define a functions,
h(x) = f(x) – A.g(x) …………………….(1)
So that h(a) = h(b) and A is a constant to be determined.
Now ,
h(a) = f(a) – Ag(a)
h(b) = f(b) – A.g(b)
So that,
f(a) – Ag(a) = f(b) – A.g(b) , which gives
A = 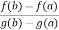 …………………………….(2)
…………………………….(2)
Now, h(x) is continuous in [a,b] as RHS of eq. (1) is continuous in [a,b] and h(x) is diff. In (a,b) as RHS of eq. (1) is diff. In (a,b)
Also,
h(a) = h(b)
Therefore all the conditions of Rolle’s theorem are satistfied then there exists a value x = cϵ (a,b)
So that h’(c) = 0
Differentiate eq.(1) w.r.t. x , we get
h’(x) = f’(x) – A.g’(x)
At x = c
h’(c) = f’(c) – A.g’(c)
0 = f’(c) – A.g’(c)
A = 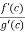
So that, we get
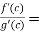
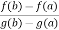 where a<c<b
where a<c<b
Hence the Cauchy’s mean value theorem is proved.
Example-7:
Verify Cauchy mean value theorems for 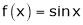 &
&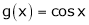 in
in 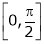
Solution:
Let 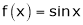 &
&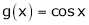 ;
; 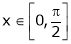
i) Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in 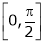
Ii) Since 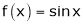 &
&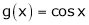
Diff. w.r.t. x we get,
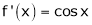 &
&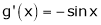
Clearly both f’(x) and g’(x) exist & finite in 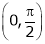 . Hence f(x) and g(x) is derivable in
. Hence f(x) and g(x) is derivable in 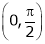 and
and
Iii) 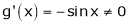
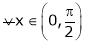
Hence by Cauchy mean value theorem, there exist at least 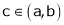 such that
such that
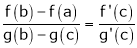
i.e. 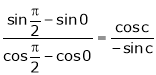
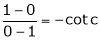
i.e. 1 = cot c

i.e. 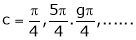
Clearly 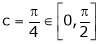
Hence Cauchy mean value theorem is verified.
Example-8:
Considering the functions ex and e-x, show that c is arithmetic mean of a & b.
Solution:
i) Clearly f(x) and g(x) are exponential functions Hence they are continuous in [a, b].
Ii) Consider 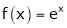 &
&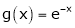
Diff. w.r.t. x we get
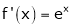 and
and 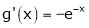
Clearly f(x) and g(x) are derivable in (a, b)
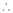 By Cauchy’s mean value theorem
By Cauchy’s mean value theorem 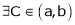 such that
such that
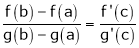
i.e. 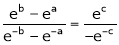
i.e. 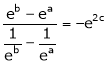
i.e. 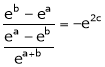
i.e. 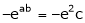
i.e. 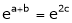
i.e. 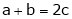
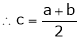
Thus 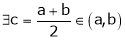
i.e. c is arithmetic mean of a & b.
Hence the result
Example-9
Show that 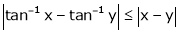
Prove that if 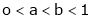
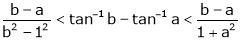 and Hence show that
and Hence show that
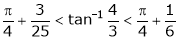
Verify Cauchy’s mean value theorem for the function x2 and x4 in [a, b] where a, b > 0
If for 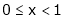 then prove that,
then prove that,
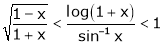
[Hint: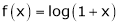 ,
, 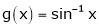 ]
]
Example-10:
Verify Cauchy’s mean value theorem for the function f(x) = x⁴ and g(x) = x² in the interval [1,2]
Sol. We are given, f(x) = x⁴ and g(x) = x
Derivative of these fucntions ,
f’(x) = 4x³ and g’(x) = 2x
Put these values in Cauchy’s formula, we get
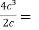
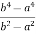
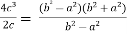
2c² = 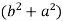
c² = 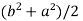
c = 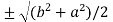
Now put the values of a = 1 and b = 2 ,we get
c = 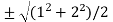 =
=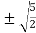 =
= 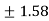 (approx..)
(approx..)
Hence the Cauchy’s theorem is verified.
Taylor’s Series Expansion:-
a) The expansion of f(x+h) in ascending power of x is
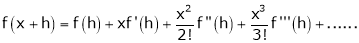
b) The expansion of f(x+h) in ascending power of h is
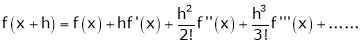
c) The expansion of f(x) in ascending powers of (x-a) is,
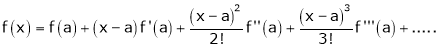
Using the above series expansion we get series expansion of f(x+h) or f(x).
Expansion of functions using standard expansions-
Example-1:
Expand 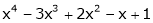 in power of (x – 3)
in power of (x – 3)
Solution:
Let 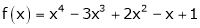
Here a = 3
Now by Taylor’s series expansion,
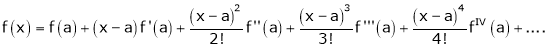 … (1)
… (1)
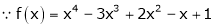
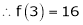
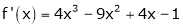
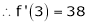
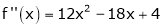
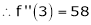
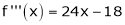
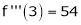
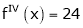
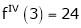
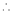 equation (1) becomes.
equation (1) becomes.
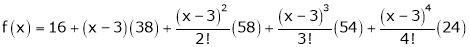
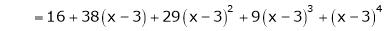
Example-2:
Using Taylors series method expand
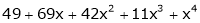 in powers of (x + 2)
in powers of (x + 2)
Solution:
Here 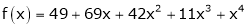
a = -2
 By Taylors series,
By Taylors series,
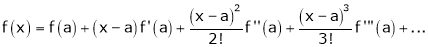 … (1)
… (1)
Since
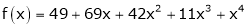
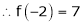
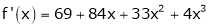
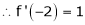
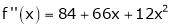
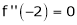
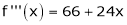
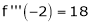
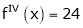
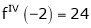 ,
, 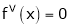 , …..
, …..
Thus equation (1) becomes
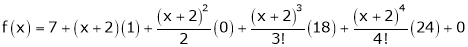
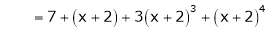
Example-3:
Expand 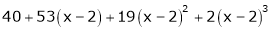 in ascending powers of x.
in ascending powers of x.
Solution:
Here
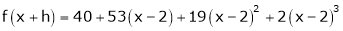
i.e. 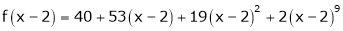
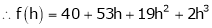
Here h = -2
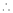 By Taylors series,
By Taylors series,
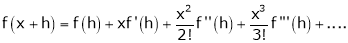 … (1)
… (1)
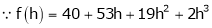
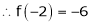
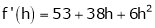
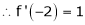
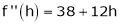
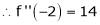
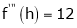
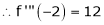
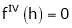
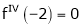
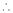 equation (1) becomes,
equation (1) becomes,
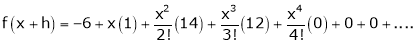
Thus
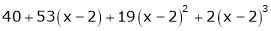
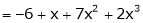
Example-4:
Expand 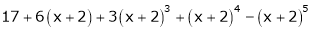 in powers of x using Taylor’s theorem,
in powers of x using Taylor’s theorem,
Solution:
Here
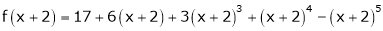
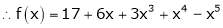
i.e. 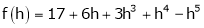
Here
h = 2
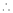 By Taylors series
By Taylors series
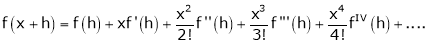 … (1)
… (1)
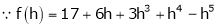
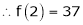
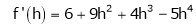
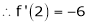
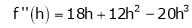
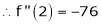
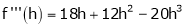
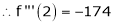
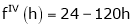
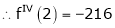
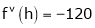
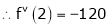
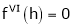
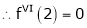
 By equation (1)
By equation (1)
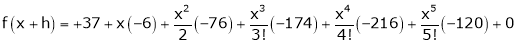
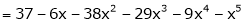
Curvature
Let M be any point on the given curve and 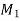 be its neighborhood.
be its neighborhood.
Let s be an arc of the curve at M and 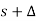 s be the arc at
s be the arc at 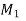 shown in the figure and
shown in the figure and 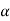 be an angle made by the tangent at point M and
be an angle made by the tangent at point M and 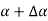 at the point
at the point 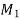 of the curve. Then the infinitely small length of the arc M
of the curve. Then the infinitely small length of the arc M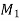 i.e.
i.e. 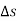 and angle made by the tangent between them is
and angle made by the tangent between them is 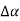 .
.
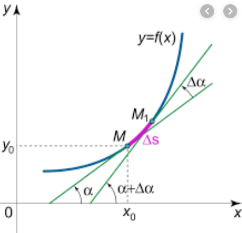
Then the curvature of the curve when M tends to  is
is 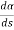
i.e. the derivative of the angle made by the tangent to the curve with respect to the arc at that point.
The unit of curvature is radian per length.
Radius of curvature: The radius of curvature is the reciprocal of the curvature of the curve at the point. It is denoted by 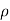 .
.
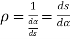
We know that slope is 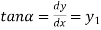
Or 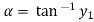
Differentiating both side with respect to x we get,
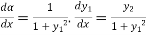
By chain rule 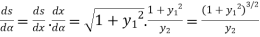
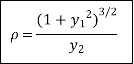 Hence
Hence
Example-1: Show that for a rectangular hyperbola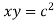 ,
, 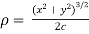 ?
?
Sol.
Given curve 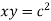 .
.
Differentiating both side with respect to x.
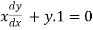
Or 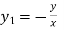 ……(i)
……(i)
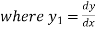
Again differentiating with respect to x.
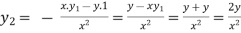 using (i)
using (i)
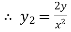 ….(ii)
….(ii)
The radius of curvature is
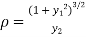
Substituting values from (i) and (ii) we get
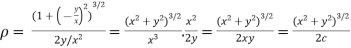 by given curve.
by given curve.
Hence 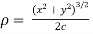 is proved.
is proved.
Example2:
Find the radius of curvature at 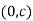 of the catenary
of the catenary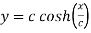 ?
?
Sol.
Given catenary 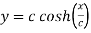 … (i)
… (i)
Differentiating (i) with respect to x.
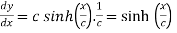
Also consider 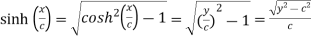
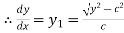 ….. (ii)
….. (ii)
Again differentiating with respect to x , we get
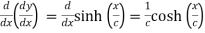
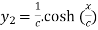 ….(iii)
….(iii)
The radius of curvature is
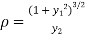
Substituting values from (i),(ii) and (iii) we get
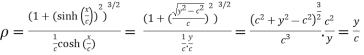
Hence the radius of curvature at 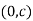 is
is 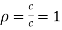 .
.
Radius of Curvature in parametric form:
Let the co-ordinates be defined in the form of functions depend on one independent variable t.
Suppose 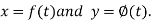
We will calculate the values in term of variables depend on t.
By chain rule we have
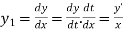
And 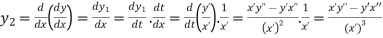
By 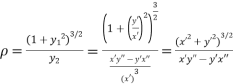
Example:
Find the radius of curvature at any point on
- Ellipse
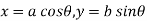 .
.
The parametric equation of the ellipse is given by
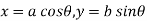
As we know by chain rule
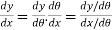
Hence 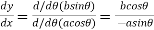
Or 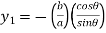 …(i)
…(i)
Again by chain rule we have
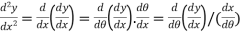
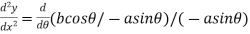
= 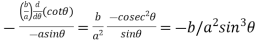
Hence 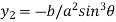 …..(ii)
…..(ii)
The radius of curvature is
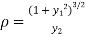
Substituting values from (i), and (ii) we get
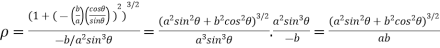 .
.
Newton’s formula for radius of curvature at origin:
- If x-axis is tangent to a curve at the origin, then
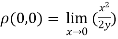
b. If y-axis is tangent to a curve at the origin, then
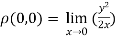
c. When the tangent is at the origin and neither on x-axis nor on y-axis then
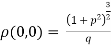
Where 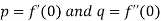 .
.
Note: To find the tangent at the origin of the curve we will equate the lowest degree term in the equation to zero.
Example: Find the radius of curvature at the origin for
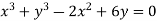
Sol.
Given curve is 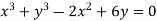 ….(i)
….(i)
Equating lowest degree term to zero we get
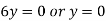 ..(ii)
..(ii)
 Tangent at the origin is on the x-axis.
Tangent at the origin is on the x-axis.
Dividing (i) by y , we get
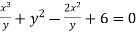
The radius of curvature at the origin on the x-axis is 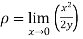 and using (ii)
and using (ii)
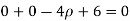
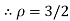 .
.
Example: Find the radius of curvature at the origin for- 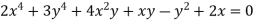
Given curve 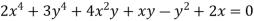 …(i)
…(i)
Equating lowest degree term to zero we get
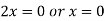 ..(ii)
..(ii)
 Tangent at the origin is on the y-axis.
Tangent at the origin is on the y-axis.
Dividing (i) by x, we get
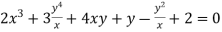
The radius of curvature at the origin on the x-axis is 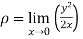 and using (ii)
and using (ii)
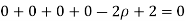
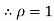 .
.
Example: Find the radius of curvature at the origin for-
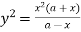
Sol. Given curve 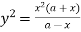
Or 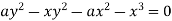 …(i)
…(i)
Equating lowest degree term to zero we get
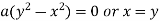 ..(ii)
..(ii)
 Tangent at the origin is neither on x-axis nor on y-axis.
Tangent at the origin is neither on x-axis nor on y-axis.
Putting in (i), 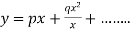 where
where 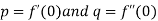 .
.
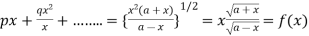
Where 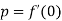
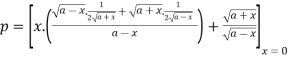
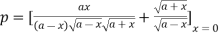
Hence 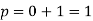
Again 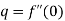

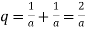 .
.
When the tangent is at the origin and neither on x-axis nor on y-axis then
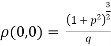
Substituting the values in p and q we get,
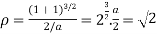 a.
a.
1.5 Envelop of a family of curves
Let us consider a family of plane curves (single-parameter) which is defined by the following equation-
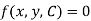
Here C is a parameter.
Then the envelope of this family of curves is a curve such that at every point it touches one of the curves of the family.
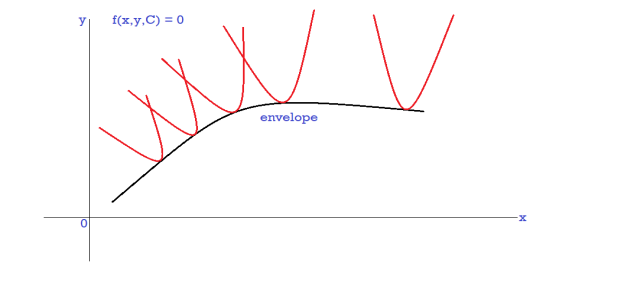
In the figure black curve is an envelope.
Note-
1. Envelope- A curve which touches each member of a family of curves is called envelope of that family of curves.
2. Envelope of a family of curves-
The locus of the ultimate points of interaction of consecutive members of a family of curve is called the envelope of the family of curves.
Example:
Find the envelope of 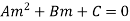 , where m is the parameter and A, B and C are function x and y.
, where m is the parameter and A, B and C are function x and y.
Sol. It is given that-
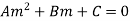 ………………….. (1)
………………….. (1)
Now differentiate equation (1) with respect to ‘m’,
We get-
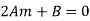 , gives
, gives
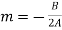
Put these values in equation (1)-
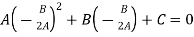
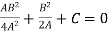
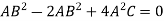
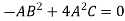
Which gives-
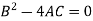
Which is the required envelope.
Example: Find the envelope of the family of 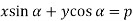 , where
, where 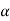 is the parameter.
is the parameter.
Sol. It is given that-
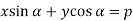 ………….. (1)
………….. (1)
Now differentiate equation (1) with respect to ‘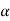 ’,
’,
We get-
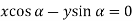 ………………… (2)
………………… (2)
Eliminate 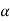 from both equations-
from both equations-
We get-
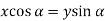
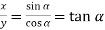
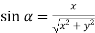 And
And 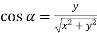
Put these values in (1) -
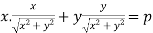
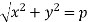
On squaring both sides, we get-
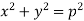
Which is the required envelope.
Example: Find the envelope of the family of straight lines 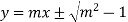 , where ‘m’ is the parameter.
, where ‘m’ is the parameter.
Sol. It is given that-
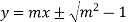
Which can be written as-
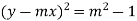
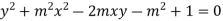
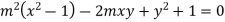 , which is a quadratic equation.
, which is a quadratic equation.
Here the value of coefficients of the quadratic equation-
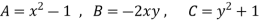
The condition for envelope in case of a quadratic equation is-
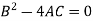
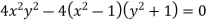
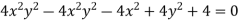
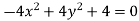
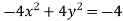
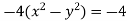
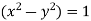
So that the envelope is 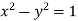
Definition- The locus of centres of curvature of a given curve is called the evolute of that curve.
The locus of the centre of curvature C of a variable point P on a curve is called the evolute of the curve and the curve itself is called involute of the evolute.
Evolute is nothing but an equation of the curve.
Method to find the evolute-
1. If a curve equation is given and we need to prove left hand side is equal to right hand side (L.H.S = R.H.S), then
First of all find the curvature C(X,Y), where
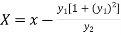
And
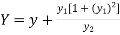
Then take left hand side and put X in place of x and Y in place of y.
2. When the curve is given and we need to find the evolute, then-
Find the curvature first and then re-write as x in terms of X and y in terms of Y and then put in the given curve
Properties of envelope and evolute-
1. The normal at any point of a curve is a tangent to its evolute touching at the corresponding centre of curvature.
2. The evolute is one only but there can be infinite involutes.
3. The difference between the radii of curvature at two points of a curve is equal to the length of the arc of the evolute between the two corresponding points.
Example: Prove that the evolute of parabola 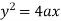 is given by
is given by 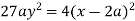
Sol. It is given that-
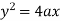
If (X,Y) are the coordinates of the centre of curvature at any point P(x , y) on the curve y = f(x), then X and Y are given as-
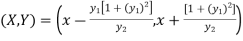 …………….. (1)
…………….. (1)
Now consider the equation of parabola (given)
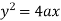
On differentiating w.r.t x-
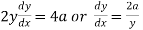
Again differentiating w.r.t.x-
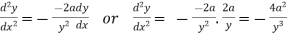
Put these derivatives in (1), we get-
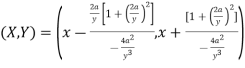
Now consider X,
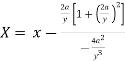
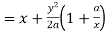
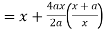
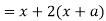
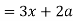
Here we get-
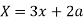
Now consider,
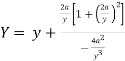
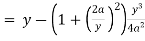
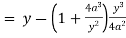
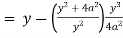
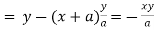
Here we get-
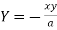
Now
Taking L.H.S of 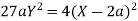
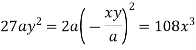
Taking R.H.S of 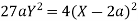
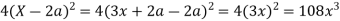
Hence proved.
Example: Find the evolute of the ellipse 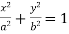 .
.
Sol. It is given that-
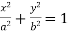
The parametric equations are 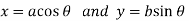
Now,
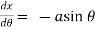 and
and 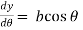
So that-
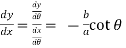
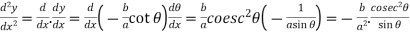
Which gives,
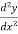
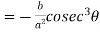
Co-ordinates of centre of curvature are (X , Y),
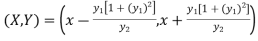 …………….. (1)
…………….. (1)
Consider X,
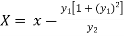
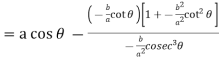
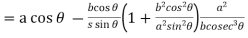
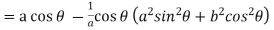
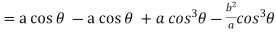
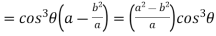
We get-
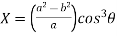
Now consider Y,
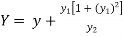
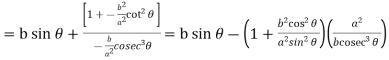
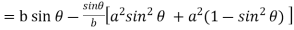
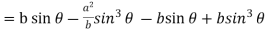
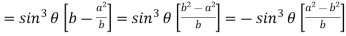
So that we get-
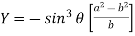
Eliminating 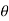 from X and Y, we get,
from X and Y, we get,
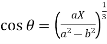 and
and 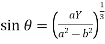
We know that 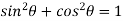
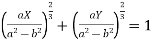
Which gives on solving-
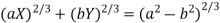
Which is the required evolute.