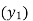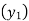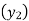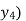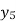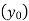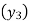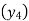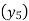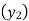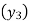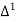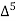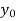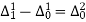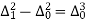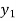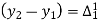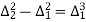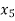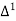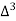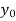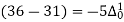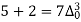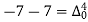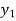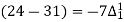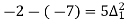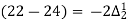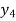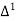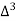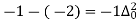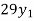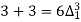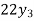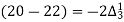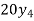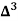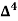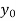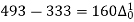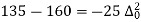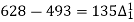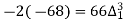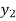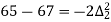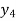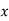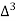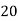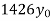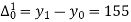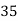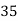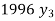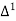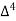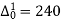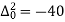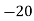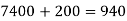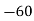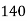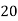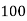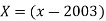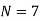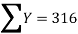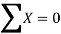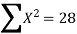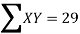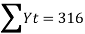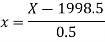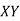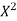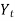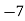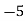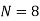UNIT 4
Interpolation and Extrapolation
Meaning
Interpolation is the process of finding a value between two points on a line or curve. To help us remember what it means, we should think of the first part of the word, 'inter,' as meaning 'enter,' which reminds us to look 'inside' the data we originally had. This tool, interpolation, is not only useful in statistics, but is also useful in science, business or any time there is a need to predict values that fall within two existing data points.
Extrapolation is defined as an estimation of a value based on extending the known series or factors beyond the area that is certainly known. In other words, extrapolation is a method in which the data values are considered as points such as x1, x2, ….., xn. It commonly exists in statistical data very often, if that data is sampled periodically and it approximates the next data point. One such example is when you are driving, you usually extrapolate about the road conditions beyond your sight.
Extrapolation is a statistical method beamed at understanding the unknown data from the known data. It tries to predict future data based on historical data. For example, estimating the size of a population a few years in the future based on the current population size and its rate of growth.
Methods
This method is simplest of all the algebraic methods, which can be used for both interpolation and extrapolation. This method is applicable under following conditions
Example 1
Write down the formula of Binomial expansion method for 4 values of y
Answer:
If known values are 4
(y – 1)4 = y4 – 4y3 + 6y2 – 4y1 + yo = 0
Example 2
Expand (y – 1)5
Answer:.
(y – 1)5 = y5 – 5y4 + 10y2 – 10y2 + 5y1 – y0= 0
Example 3
From the following data estimate the production for the year 2001 and 2005 by binominal expansion method
Year | 1995 | 1997 | 1999 | 2001 | 2003 | 2005 |
Production(000’s tons) | 20 | 40 | 70 | ? | 130 | ? |
Solution
Let X and Y be year and production.
Year | 1995 | 1997 | 1999 | 2001 | 2003 | 2005 |
Production(000’s tons) | 20 | 40 | 70 |
| 130 ( |
|
Since the known values of Y are four, the fourth order leading differences will be zero.
i.e. 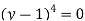 or
or 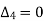

The second equation can be obtained by increasing the suffixes of each term of y by one and keeping the coefficients same. We get
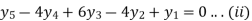
From equation (i) 
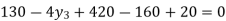
On simplification, 
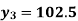
i.e., Production for the year 2001 is 102.5 (000’ tons)
From (ii) 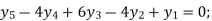 Here
Here 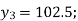
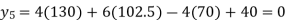


The production for the year 2005 is 145(000’ tons)
Example 4
From the following data estimate probable life expectancy of an average Indian for the years 1980 and 2010
Birth year | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 | 2010 |
Life expectancy (in year) | 68.2 | 69.7 | 70.8 | ? | 75.4 | 77 | ? |
Solution
Let X and Y be birth year and life expectancy.
Birth year | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 | 2010 |
Life expectancy (in year) | 68.2 | 69.7 | 70.8 |
| 75.4 | 77 |
|
Since the know n values ae 5, the estimation is based on the expansion of
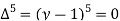
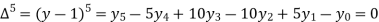
We have to determine the value of 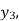

On simplification, 

Hence the probable life expectancy for the year 1980 is 72.77 years.
Now expand 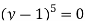 with change of subscript and keeping coefficients as it is.
with change of subscript and keeping coefficients as it is.
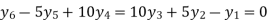
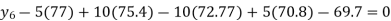
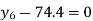
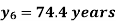
Example 5
Working class cost of living indices of a certain place for some years are given below. Interpolate the missing index number for 1995 and 1999
Year | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
Index No. | 320 | 300 | ? | 280 | 278 | 250 | ? |
Solution
Let X and Y be year and index number.
Year | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
Index No. | 320 | 300 |
| 280 | 278 | 250 |
|
Since the known values are 5, the fifth leading differences will be zero, i.e,, 

And the second equation can be obtained by, increasing the suffixes of each term of y by one, keeping the coefficients same:
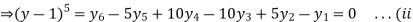 )
)
We have to determine the value of  from equation (i)
from equation (i)

On simplification 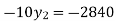
 .Hence the missing Index number for 1995 is 284. From(ii)
.Hence the missing Index number for 1995 is 284. From(ii)
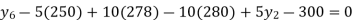
Here 

 .Hence the Index number for 1990 is 150.
.Hence the Index number for 1990 is 150.
Newton’s language
This method is applicable in those cases where the independent variable X increases by equal intervals. But, like binominal expansion method it is necessary that the value Y which is to be interpolated corresponds to one of the given values of X.
Formula
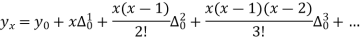
If the ‘x’ series is in descending order. Convert them in an ascending order and then apply Newton formula.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The formula to find the value of’x’ in finding the missing value of’y’ using Newton’s method of interpolation

For a time series data,
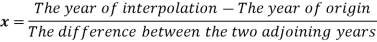
Example 1
Use Newton’s method to find the number of employees whose wages ₹ 600 per day
Wages | 300 | 500 | 700 | 900 | 1100 |
No. of Employees | 36 | 31 | 24 | 22 | 18 |
Solution
Wages | No.of employees |
|
|
|
| |
300 | 36 |
|
|
|
|
|
500 | 31 |
|
|
|
|
|
700 | 24 |
|
|
|
|
|
900 | 22 |
|
|
|
|
|
1100 | 18 |
|
|
|
|
|
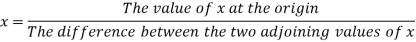

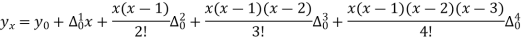
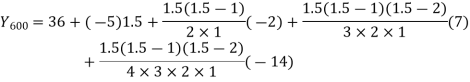



27 employees earning 600 per day.
Example 2
The following table shows the expectation of life at different ages. Find the expectation of life at age 26.
Age | 15 | 20 | 25 | 30 | 35 |
Expectation of life | 30 | 29 | 27 | 22 | 20 |
Solution
Age | Expectation life |
|
|
|
|
15 |
|
|
|
|
|
20 |
|
|
|
|
|
25 |
|
|
|
|
|
30 |
|
|
|
|
|
35 |
|
|
|
|
|
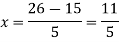

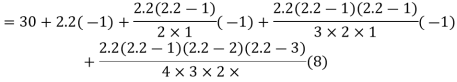
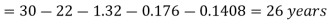
The expectation of life at 26 years is 26 years.
Example 3
Find the number of persons below the age of 70 years from the following data
Age in years | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
No of persons | 333 | 160 | 135 | 67 | 65 |
Solution
Age below | No.of Persons |
|
|
|
| |
20 | 333 |
|
|
|
|
|
40 | 493 |
|
|
|
|
|
60 | 628 |
|
|
|
|
|
80 | 695 |
|
|
|
|
|
100 | 760 |
|
|
|
|
|

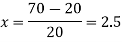
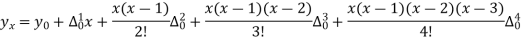
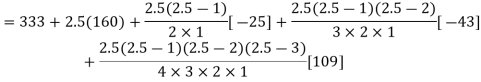

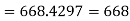
There are 668 people below age of 70 years.
Example 4
Following is data regarding annual net life insurance premium. Using Newtons method estimate the premium at the age of 26 years.
Age(years) | 20 | 25 | 30 | 35 |
Annual net premium (in Rs) | 1426 | 1581 | 1771 | 1996 |
Solution
Let x and y be the age and annual net premium.
The number of known values of ‘y’ n = 4, so prepare leading differences up to Δ3
|
| Leading differences | ||
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Here 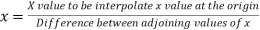
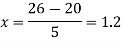

The Newton’s equation of interpolation is
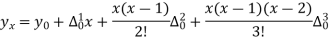
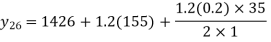
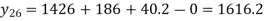
1616.2 is premium at the age of 26 years.
Example 5
From the following data estimate the number of persons earning wages below Rs. 90 per day.
Wages per day | Below 40 | 40-60 | 60-80 | 80-100 | 100-120 |
No. of persons | 500 | 240 | 200 | 140 | 100 |
Solution
Let x and y be the wages per day and no. of persons. Here class intervals are converted into less than / below type, because ‘y’ value to be interpolate is below 90 then prepare the leading difference table upto Δ4, since there are n = 5 known values of y.
Wages below x |
| Leading differences | |||
|
|
|
| ||
| 500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Here


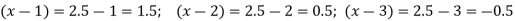
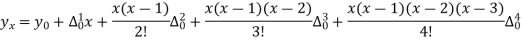
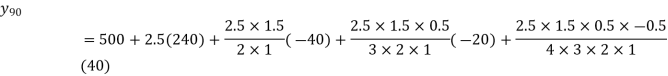
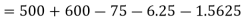

Key takeaways –
Introduction:
A time series is set of data collected at successive point in a time or over successive period of time.A time series is a collection of observations made sequentially through time.The interval between observations can be any time interval (hours within days, weeks, months, years, etc.).
Some examples of time series are:
a) An analysis of a single sequence of data is called univariate time-series
analysis.
b) An analysis of several sets of data for the same sequence of time periods is called multivariate time-series analysis or, more simply, multiple time-series analysis.
Utilities of time series:
1. It helps in understanding past behaviour and is useful for prediction of future.
2. It facilitates comparison.
3. The various components of time series are useful to study the effective change under each component.
4. The reasons for variation can be studied by comparing actual with expected results.
COMPONENT OF TIME SERIES:
Fluctuation in a time series is mainly due to four basic components.
1 Secular trend or trend (T).
2 Seasonal variation (S).
3 Cyclical variation or cyclic fluctuation (C).
4 Irregular or random moments (I).
Secular trend or trend (T):
Upward sloping trend paths in a real- value time series may be indicative of growth phenomenon, a downward sloping path suggest contraction.
3. In a money-value time series an upward sloping path may represent some combination of real growth and inflation; a downward sloping trend path might indicate contraction with deflation.
4. Trend is usually the result of long-term factors such as changes in the population, demographics, technology, or consumer preferences.
Seasonal Variation:
Cyclic Components:
Irregular Variation-
Key takeaways –
A moving average is a technique to get an overall idea of the trends in a data set; it is an average of any subset of numbers. The moving average is extremely useful for forecasting long-term trends. You can calculate it for any period of time. For example, if you have sales data for a twenty-year period, you can calculate a five-year moving average, a four-year moving average, a three-year moving average and so on. Stock market analysts will often use a 50 or 200 day moving average to help them see trends in the stock market and (hopefully) forecast where the stocks are headed.
An average represents the “middling” value of a set of numbers. The moving average is exactly the same, but the average is calculated several times for several subsets of data. For example, if you want a two-year moving average for a data set from 2000, 2001, 2002 and 2003 you would find averages for the subsets 2000/2001, 2001/2002 and 2002/2003. Moving averages are usually plotted and are best visualized.
Year | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
Number of students | 332 | 317 | 357 | 392 | 402 | 405 | 410 | 427 | 435 | 438 |
Solution:
Computation of three- yearly moving averages.
Year | Number of students | 3-yearly moving total | 3-yearly moving averages |
1995 | 332 | --- | --- |
1996 | 317 | 1006 | 335.33 |
1997 | 357 | 1066 | 355.33 |
1998 | 392 | 1151 | 383.67 |
1999 | 402 | 1199 | 399.68 |
2000 | 405 | 1217 | 405.67 |
2001 | 410 | 1242 | 414.00 |
2002 | 427 | 1272 | 424.00 |
2003 | 435 | 1300 | 433.33 |
2004 | 438 | --- | --- |
Example 9.5
Calculate four-yearly moving averages of number of students studying in a higher secondary school in a particular city from the following data.
Year | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 |
Sales | 124 | 120 | 135 | 140 | 145 | 158 | 162 | 170 |
Solution:
Computation of four- yearly moving averages.
Year | Sales | 4-yearly centered moving total | 4-yearly moving average | 4-yearly centered moving average |
2001 | 124 | --- | --- | --- |
|
|
|
|
|
2002 | 120 | --- | -- | --- |
|
| 519 | 129.75 |
|
2003 | 135 | -- |
| 132.37 |
|
| 540 | 135.00 |
|
2004 | 140 | -- |
| 139.75 |
|
| 578 | 144.5 |
|
2005 | 145 | -- |
| 147.87 |
|
| 605 | 151.25 |
|
2006 | 162 | -- |
| 162.50 |
|
| 635 | 166.25 |
|
2007 | 162 | -- |
| 162.50 |
|
| 665 | 166.25 |
|
2008 | 170 | -- | -- | -- |
|
|
|
|
|
2009 | 175 | -- | -- | - |
Method of Least Square
The line of best fit is a line from which the sum of the deviations of various points is zero. This is the best method for obtaining the trend values. It gives a convenient basis for calculating the line of best fit for the time series. It is a mathematical method for measuring trend. Further the sum of the squares of these deviations would be least when compared with other fitting methods. So, this method is known as the Method of Least Squares and satisfies the following conditions:
(i) The sum of the deviations of the actual values of Y and Ŷ (estimated value of Y) is Zero. that is Σ(Y–Ŷ) = 0.
(ii) The sum of squares of the deviations of the actual values of Y and Ŷ (estimated value of Y) is least. that is Σ(Y–Ŷ)2 is least ;
Procedure:
(i) The straight line trend is represented by the equation Y = a + bX …(1)
where Y is the actual value, X is time, a, b are constants
(ii) The constants ‘a’ and ‘b’ are estimated by solving the following two normal
Equations ΣY = n a + b ΣX ...(2)
ΣXY = a ΣX + b ΣX2 ...(3)
Where ‘n’ = number of years given in the data.
(iii) By taking the mid-point of the time as the origin, we get ΣX = 0
(iv) When ΣX = 0 , the two normal equations reduces to


The constant ‘a’ gives the mean of Y and ‘b’ gives the rate of change (slope).
(v) By substituting the values of ‘a’ and ‘b’ in the trend equation (1), we get the Line of Best Fit.
Fit a straight-line trend by the method of least squares and tabulate the trend values.
Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 |
Prod. Of Sugarcane | 40 | 45 | 46 | 42 | 47 | 50 | 46 |
Solution:
Computation of trend values by the method of least squares (ODD Years).
Year(x) | Production of Sugarcane(Y) |
|
|
| Trend values |
2000 | 40 | -3 | 9 | -120 | 42.04 |
2001 | 45 | -2 | 4 | -90 | 43.07 |
2002 | 46 | -1 | 1 | -46 | 44.11 |
2003 | 42 | 0 | 0 | 0 | 45.14 |
2004 | 47 | 1 | 1 | 47 | 46.18 |
2005 | 50 | 2 | 4 | 100 | 47.22 |
2006 | 46 | 3 | 9 | 138 | 48.25 |
|
|
|
|
|
|

Therefore, the required equation of the straight-line trend is given by
Y = a+bX;
Y = 45.143 + 1.036 (x-2003)
The trend values can be obtained by
When X = 2000, Yt = 45.143 + 1.036(2000–2003) = 42.035
When X = 2001, Yt = 45.143 + 1.036(2001–2003) = 43.071,
similarly, other values can be obtained.
2. Given below are the data relating to the sales of a product in a district.
Fit a straight-line trend by the method of least squares and tabulate the trend values.
Year | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
Sales | 6.7 | 5.3 | 4.3 | 6.1 | 5.6 | 7.9 | 5.8 | 6.1 |
Solution:
Computation of trend values by the method of least squares.
In case of EVEN number of years, let us consider

Year | Sales (Y) |
|
|
| Trend value ( |
1995 | 6.7 |
| 46.9 | 49 | 5.6166 |
1996 | 5.3 |
| 36.5 | 25 | 5.7190 |
1997 | 4.3 |
| 12.9 | 9 | 5.8214 |
1998 | 6.1 |
| 6.1 | 1 | 5.9238 |
1999 | 5.6 |
| 39.2 | 49 | 6.0261 |
2000 | 7.9 |
| 39.5 | 25 | 6.1285 |
2001 | 5.8 |
| 17.4 | 9 | 6.2309 |
2002 | 6.1 |
| 6.1 | 1 | 6.3333 |
| 47.8 |
| 194.6 | 168 |
|
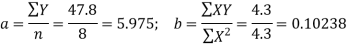
Therefore the required equation of the straight line trend is given by

When 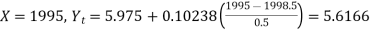
When 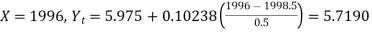
Similarly other values can be obtained.
Business forecasting
Forecasting is a method or a technique for estimating future aspects of a business or the operation. It is a method for translating past data or experience into estimates of the future. It is a tool, which helps management in its attempts to cope with the uncertainty of the future. Forecasts are important for short-term and long-term decisions. Businesses may use forecast in several areas: technological forecast, economic forecast, demand forecast. There two broad categories of forecasting techniques: quantitative methods (objective approach) and qualitative methods (subjective approach). Quantitative forecasting methods are based on analysis of historical data and assume that past patterns in data can be used to forecast future data points. Qualitative forecasting techniques employ the judgment of experts in specified field to generate forecasts. They are based on educated guesses or opinions of experts in that area. There are two types of quantitative methods: Times-series method and explanatory methods.
Time-series methods make forecasts based solely on historical patterns in the data. Time-series methods use time as independent variable to produce demand. In a time series, measurements are taken at successive points or over successive periods. The measurements may be taken every hour, day, week, month, or year, or at any other regular (or irregular) interval. A first step in using time-series approach is to gather historical data. The historical data is representative of the conditions expected in the future. Time-series models are adequate forecasting tools if demand has shown a consistent pattern in the past that is expected to recur in the future. For example, new homebuilders in US may see variation in sales from month to month. But analysis of past years of data may reveal that sales of new homes are increased gradually over period of time. In this case trend is increase in new home sales.
Key Takeaways:
Reference-