UNIT 2
Runoff and Hydrographs
- Runoff may be referred to as stream flow, river discharge or catchment yield. It is normally expressed as volume per unit time.
- Based on the time delay between precipitation and runoff, runoff is classified into two categories –
(1) Direct runoff
(2) Base flow runoff
Direct Runoff:
It is that part of runoff which enters the stream immediately after the precipitation. It includes surface runoff, prompt interflow and precipitation on the channel surface. It is sometimes termed as direct storm Turnoff or storm runoff.
Surface Runoff
It has two components
(1)Overland flow (flow of water over land before joining any open channel)
(2) Open channel flow
Over land flows are small and the flow is taken to be in laminar region. Length of overland flow is generally small.
Open channel flows are in turbulent region
Interflow
- Water which infiltrates the soil surface and then moves laterally through the upper soil horizons towards the stream channels above the main groundwater table is known as the interflow. It is also known as subsurface runoff, subsurface storm flow, storm seepage and secondary base flow.
- If the lateral hydraulic conductivity of the surface layers is substantially greater than the overall vertical hydraulic conductivity, it is a favorable condition for the generation of interflow. Generally interflow moves more slowly than surface runoff
- Depending upon the time delay between infiltration and its outflow from the upper crusts of the soil, the interflow is sometimes classified into prompt. Interflow and delayed interflow
Direct Precipitation:
Direct precipitation into the water surface and into the stream channels will normally represent only a small percentage of total volume of water flowing in the streams. This component is usually ignored in runoff calculations.
BASE FLOW OR GROUND WATER FLOW:
- The delayed flow that reaches a stream essentially as groundwater called base flow. Many times delayed interflow is also included under this category.
- The infiltrated water which percolates delay becomes ground and when groundwater table rises and intersects the stream channels of the basin it discharges into as a the groundwater runoff
- Ground water flow is sometimes referred to as base flow, draw down, effluent seepage. For the practical purpose of analysis total runoff in stream channel is generally classified as direct runoff and base flow.
Key takeaways
Runoff have basically two types
- Direct runoff
- Surface runoff
- Interflow
- Direct precipitation
- Base flow runoff
2.1.1 Runoff Characteristics of Stream
On the basis of hydrograph studies, a stream can be classified a
(a) Perennial
(b) Intermittent
(c) Ephemeral
Perennial Stream
- A perennial stream is any which always carries some flow throughout the year. Even during dry seasons the water table will be above the bed of the stream. Thus, considerable amount of ground water flow occurs during non precipitation period.
- In perennial streams, 100% dependable flow has a finite value
- Time Vs discharge graph
Intermittent Stream
- Intermittent stream has limited contribution from the groundwater.
- Stream remains dry for most part of dry months
- Base flow (ground water flow) occurs significantly during wet season.
- During dry seasons the water table drops to a level lower than that of the stream bed.
Ephemeral Stream
- An ephemeral stream is one which does not have any base-low contribution
- Annual hydrograph shows series of short-duration spikes marking flash flow in response to storms
- The stream becomes dry soon after the end of the storm flow.
- An ephemeral stream does not have any well defined channel
- Most rivers in arid Zones are of the ephemeral kind.
- In Intermittent ephemeral streams Q100 (100% dependable flow) zero (0)
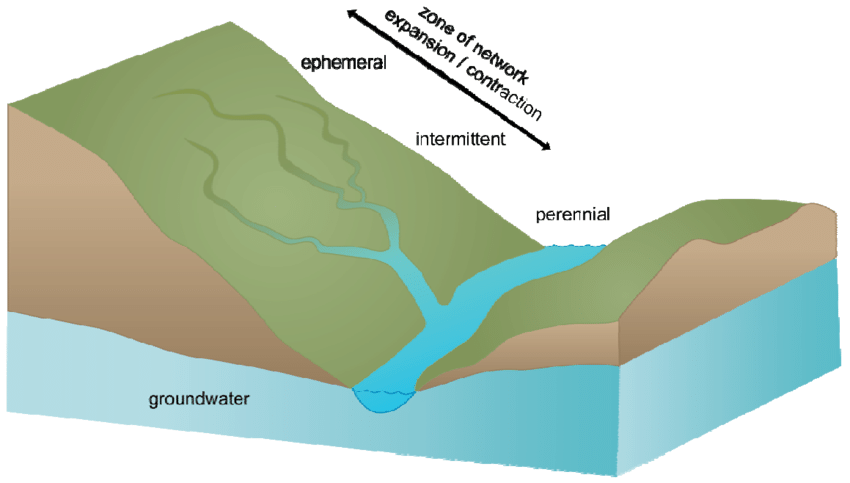
Fig. 1: Runoff characteristic of stream
Key takeaways
On the basis of hydrograph studies, a stream can be classified a
(a) Perennial
(b) Intermittent
(c) Ephemeral
2.1.2 Mass Curve
A graph of the cumulative value of any hydrologic quantity, generally as the ordinate, plotted against the time as abscissa is known as a mass curve. When cumulative volume of runoff taken as the hydrologic quantity, the mass curve may be called a flow mass curve or simply a mass curve .it is the integration of the hydrograph and therefore represents the area under the hydrograph from one time to another. Mathematically, the mass curve, is expressed by
V (t) = integration within limit 0to t Q (t) DT
Where V (t) = Cumulative volume of flow up to time from the start of the record, that is, the ordinate of the mass curve at any time t.
Q (t) - discharge as a function of time, i.e., the ordinate of the hydrograph
When it is desired to use water at uniform or nearly. Uniform rate greater than the minimum discharge in the stream, it is necessary to provide storage where water is impounded during periods. Of high flow for use during periods of low flows, Mass curve serves as a very useful tool to determine the required storage capacity for any uniform rate of demand.
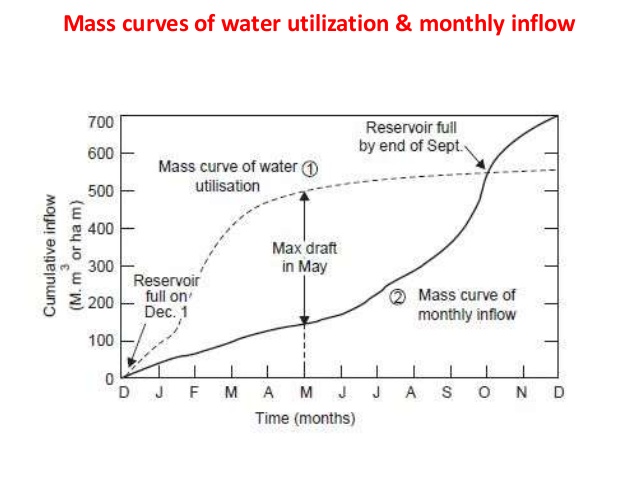
Fig. 2: Mass curve
Storage Capacity Determination
- The difference in the ordinates of any two points on the curve is the summation of the flow during the intervening period of time. Thus, if two points such as Panda Qin figure are joined by a straight line, the slope of the line PQ would give the average rate of flow during the period t5 to t7.
- The rate of flow at any time is indicated by the slope of the tangent drawn to the mass curve at the corresponding time.
- If the mass curve is horizontal. i.e., having zero slopes, for a particular period of time it means that there is no discharge in the stream during that period.
- The rate of demand is the rate at which water is required for any use. A straight line having the slope equal to this rate is called a demand line or draft line or use line.
Where the mass curve is steeper than the draft line, the flow in the streaming at a higher rate than the rate of draft and consequently some of the stream flow is available for, storage or it will spill if the reservoir is already full.
- Where the mass curve has flatter slope than the draft line. Water will be drawn from storage in order to maintain the required rate of draft.
The storage required to meet any given draft rate may be found out from mass curves as follows
- Let the line OJ represent the cumulative demand the slope of which is equal to the rate of draft. Let us. Assume that the reservoir is full at the beginning.
- From O to the mass curve is steeper than OJ, indicating that the flow rate into the reservoir is more than the draft rate.
- Since the reservoir is already, full, no water can be 'stored though there is surplus water. Hence, the reservoir will be overflowing during the period from 0 to t.
- The ordinate AA' indicates the total volume of the. Spill in this period.
- From A onwards the mass curve is flatter than OJ. So withdrawals from the reservoir start from the time t1.
- As the amount of water indicated by AA is already wasted, it cannot be included further in the analysis for the purpose of cumulative inflow. So all the inflows into the reservoir and the withdrawals from it are to be reckoned from A in other words. The origin will be shifted from O to A.
- So a line drawn parallel to OJ and tangential to mass curve at A that is AC, will now become the Cumulative demand.
- From A to B the mass curve is flatter than OJ. The reservoir is continuously depleted from t1 to t2 and S1 the vertical intercept between the line AC and B would indicate the maximum withdrawal from it. Thus S, determines the storage requirement for the dry period , to t
- From B to D the mass curve is, again steeper than OJ and the reservoir starts filling from t2 and it will be full at t3, S1 may be more easily measured as the vertical intercept between the two tangent lines AC and BM. Which are parallel to OJ and drawn to the mass curve at peak (or the ridge) point A and the trough (or the valley) point B
- Again the reservoir will be overflowing from t3 to t4 and DD' indicates the amount of spill during this period.
- At D, the situation is identical to what it was at A.
- Therefore the vertical intercept S2 between the two tangents DF and EN gives the storage requirement for the dry period t4 to t6.
- If the flow data for a large time period is available, the tangent lines are drawn at other ridge points and the storages are determined. The largest of these storages is then taken to be the actual storage requirement. That is,
S Maximum of (S1, S2, S3,)
DETERMINATION OF MAINTAINABLE MAX DEMAND RATE
- Mass curve can also be used to solve the reverse problem of determining the maximum demand rate that can be maintained by a given storage volume. However, it is a trial and error procedure,
- Straight lines tangential to the first peak point of the mass curve are drawn with different trial slopes such that all of them intersect the mass curve at or below the next higher peak point.
- The slope of the line for which the vertical intercept between itself and the touch point is equal to given storage defines the possible maximum draft rate that can be maintained.
- Similar straight lines are drawn at other ridge points across the subsequent valleys and the possible demand rates are obtained.
- The smallest of the various demand rates thus found gives the maximum demand rate that can be maintained by a given storage.
Residual Mass Curve
- In the residual mass curve, cumulative net inflow into the Reservoir i.e. the difference between the cumulative runoff and the emulative demand, is plot against time as shown in figure. In such a curve the inclined draft line O of previous figure is transformed into the horizontal line OJ of as shown in figure below and so are the tangent lines AC, BM and DP and EN. The storage required for the first dry period is now given as the difference between the ordinates of the residual mass gory at A and B and for the next dry period as that between the ordinates of D and E.
Key takeaways
In mass curve determines the
- Storage Capacity Determination
- Determination of maintainable max demand rate
2.2.1 Hydrograph
(1) A plot of the discharge in a stream plotted against time chronologically is called a hydrograph. Depending upon the unit of time involved, we have
(2) Annual hydrograph -it shows variation of daily weakly or mean flow of any no. Of successive days over a year.
(3) Monthly hydrograph- it shows the variation of daily mean flow over a month.
(4) Seasonal hydrograph- it shows the variation of the discharge in a particular season such, as the monsoon season or dry season.
(5) Flood hydrographs or hydrographs due to a storm -it shows stream flow due to a storm over a catchment Hydrographs 1,2 and 3 as above are called long term hydrographs and are used for long term studies like.
(a) Calculating the surface water potential of stream,
(b) Reservoir studies and
(c) Drought studies
Flood hydrograph on the other hand is upped to study the flooding characteristics of a stream. It is a short term study.
Beginning of Water Year
The time when precipitation exceeds the average evapotranspiration losses is called the beginning of water year. 1st June in India is considered beginning of water year, beginning of water year is decided such that flood season is not divided between successive years.
2.2.2 Factors affecting Flood Hydrographs
Rainfall characteristics
Type of Precipitation
- It occurs either as rainfall or as snowfall. Precipitation falling as rain contributes directly to runoff. Hail and sleet which melt rapidly after contact with the ground may also contribute immediately. Precipitation falling as snow, in winter months, will not contribute to runoff until melting occurs.
Rainfall Intensity
- Heavy rain falling in excess of the infiltration capacity of the soil will largely contribute to surface runoff and will therefore tend to reach the stream channels very rapidly while the rain falling at lower intensities will cause delayed runoff.
Rainfall Duration
- If the rainfall duration is equal to or greater than time of concentration (Tc ie. The time in which the entire catchment starts contributing to runoff) the potential runoff is at a maximum. On the other hand, if the duration of rainfall is less than T c then the potential runoff will be lower than the maximum because only part of the catchment will be contributing to runoff before the rainfall ceases
- Also, since infiltration capacity is maximum at the beginning of rainfall and tends to decrease through the period of rainfall until it attains a constant value, the longer the rain continues, the smaller will the infiltration capacity become, and the greater the amount of surface runoff is likely to be.
Rainfall Distribution
- The time relationship between rainfall and runoff may be great affect by the distribution of rainfall over the catchment area a uniformly distributed rainfall volume may lead to delay runoff then the same volume falling over a localized part of catchment.
- The first type of rainfall distribution will tend to result in an increased groundwater flow and consequently a long-term increase in stream flow, while the latter type of distribution will tend to give large volumes of surface runoff and thus, a more sudden, sort-lived increase in stream flow.
Catchment Factors
Factors such as shape, topography and soil type remain constant over long periods while others such as land use etc. May change radically and so profoundly influenced runoff.
- Shape of the catchment area influences the time of concentration of the catchment
- Catchment shape is quantitatively expressed as form factor and compactness factor.
- The form factor is derived by dividing the average width of the catchment by its axial length measured from the outlet to the most remote point
- A long, narrow catchment will yield a low value of the form factor, and generally a lower-peak runoff total than a similar sized area with a high form factor.
- The compactness coefficient is derived by dividing the periphery of the watershed by the circumference of the form circle whose area equals that of the catchment, and thus has a theoretical minimum value of unity for a completely circular catchment. The lower the value of the coefficient, the more rapidly is water likely to be discharged from the catchment area via the main streams.
Slope of the Catchment Area
- If slope of catchment area is large, water moves faster over the surface and channel towards the stream channel. Hence runoff peak comes early.
Geology
- Coarse textured, sandy soils will tend to give rise to little runoff. On the other hand fine grained closely compacted clay soil will tend to yield more surface runoff. Moisture content of soil also affects runoff through its effect on infiltration capacity
Vegetation
- The most important effect of the vegetal cover is to slow down the movement of water over the surface after rainfall, thus, allowing more time for infiltration to take place. The timing of runoff after rainfall may be considerably modified and. Furthermore, peak stream flow a will tend to be much lower.
Drainage Network
- Closely spaced streams allow efficient drainage of precipitated water, and in such cane overland flow will be short and surface runoff will rapidly reach the mains streams.
Direction of Storm Movement
- The runoff from a basin is influenced by the direction of storm movement. If a storm striking a long and narrow basin is moving in an upstream direction the runoff contributed by the lower tributaries would have been already drained out by the time the runoff from the middies and upper tributaries reaches the basin outlet and therefore less peak discharge would be observed in this case.
- When, on the other hand, the storm moves downstream the runoff peaks from the individual tributaries are more likely to arrive at the basin outlet at approximately the same time with the result the runoff peak will be many times more than that in the case of storm moving
- A storm crossing the basin in the transverse direction would produce peak discharge which would be somewhere between the peaks produced by the two cases described above.
COMPONENTS OF HYDROGRAPHS
Components of Hydrograph:
Hydrograph generally contains the following three parts.
1. Rising Limb
2. Peak (or Crest) Segment
3. Falling (or Recession) Limb
1. Rising Limb: It is the ascending curved portion of the hydrograph. The rising limb rises slowly in the early stage of the flood but more rapidly toward the end portion. The shape of rising limb depends on duration and intensity distribution of rainfall. This is because in early stages the losses is more and water reaches to the stream faster.
2. Peak Segment (or Crest Segment): Peak segment is shown by inverted U in the hydrograph. This is the part which is taken as matter of interest by hydrologists. Peak of hydrograph occurs when all parts of basins contribute at the outlet simultaneously at the maximum rate. Depending upon the rainfall-basin characteristics, the peak may be sharp, flat or may have several well defined peaks.
3. Falling Limb (or Recession Limb): Recession Limb represents the withdrawal of water from the storage built up during the early phase of hydrograph. It extends from the point of inflection at the end of the crest to the beginning of the natural groundwater flow. The shape of recession limb depends upon basin characteristics only and independent of the storm.
Key takeaways
Factor affecting hydro graphs is
- Type of precipitation
- Rainfall intensity
- Rainfall duration
- Rainfall distribution
- Catchment factors
- Slope of catchment area
- Geology
- Vegetation
- Drainage network
- Direction of storm movements
- The role of unit hydrograph in hydrology is to provide an estimate of direct runoff hydrograph resulting from given excess rainfall hyetographs
- In order to use unit hydrograph as a tool for predicting direct runoff hydrograph, we first need to derive a unit hydrograph for a given watershed.
- This method was first suggested by Sherman in 1932 and has undergone many refinements since then.
- A unit hydrograph is defined as they hydrograph of direct runoff resulting from one unit depth (1 cm) of rainfall excess occurring uniformly over the basin and at a uniform rate for a specified duration (D hours). OR
- A unit hydrograph (UH) is the hypothetical unit response of a watershed (in terms of runoff volume and timing) to a unit input of rainfall. It can be defined as the direct runoff hydrograph (DRH) resulting from one unit (e.g.,1 cm) of effective rainfall occurring uniformly over that watershed at a uniform rate over a unit period of time. As a UH is applicable only to the direct runoff component of a hydrograph (i.e., surface runoff), a separate determination of the base flow component is required. OR
- It can be defined as the direct runoff hydrograph (DRH) resulting from one unit (e.g., 1 cm) of effective rainfall occurring uniformly over that watershed at a uniform rate over a unit period of time.
- A UH is specific to a particular watershed and specific to a particular length of time corresponding to the duration of the effective rainfall. That is, the UH is specified as being the 1-hour, 6-hour, or 24-hour UH, or any other length of time up to the time of concentration of direct runoff at the watershed outlet. Thus, for a given watershed, there can be many unit hydrographs, each one corresponding to a different duration of effective rainfall
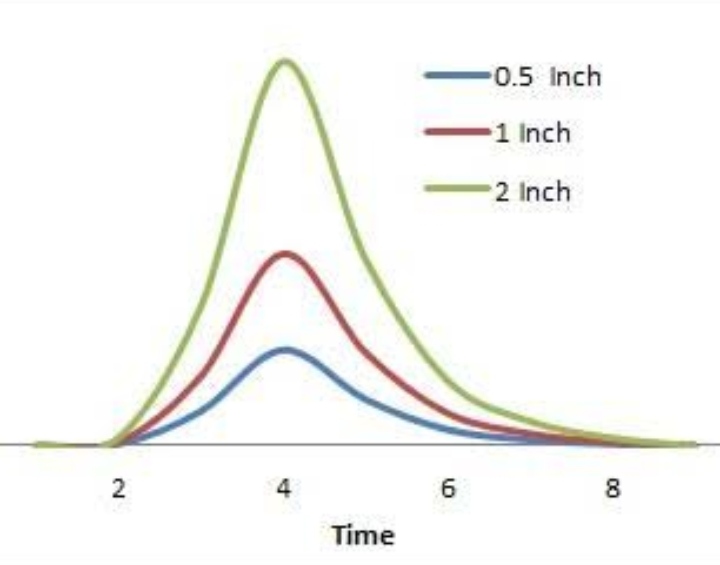
Fig. 3: Unit hydrograph
The following are essential steps in deriving a unit hydrograph from a single storm:
- Separate the base flow and obtain the direct runoff hydrograph (DRH).
- Compute the total volume of direct runoff and convert this volume into the equivalent depth of effective rainfall (in 1 cm) over the entire basin.
- Normalize the direct runoff hydrograph by dividing each ordinate by the equivalent volume (cm) of direct runoff (or effective rainfall)
- Determine the effective duration of excess rainfall. To do this, obtain the effective rainfall hyetograph (e.g., use the φ-index, the Horton) and its associated duration. This duration is the duration associated with the unit hydrograph
- Unit hydrographs are fundamentally linked to the duration of the effective rainfall event producing them. They can only be used to predict direct runoff from storms of the same duration as that associated with the UH, or from storms which can be described as a sequence of pulses, each of the same duration as that associated with the UH.
- An S-hydrograph represents the response of the basin to an effective rainfall event of infinite duration. Assume that a UH of duration D is known and that a UH for the same basin but of duration D’ is desired. The first step is to determine the S-curve hydrograph by adding a series of (known) UH’s of duration D, each lagged by a time interval D. The resulting superposition represents the runoff resulting from a continuous rainfall excess of intensity 1/D.
- Lagging the S-curve in time by an amount D’ and subtracting its ordinates from the original unmodified S-curve yields a hydrograph corresponding to a rainfall event of intensity 1/D and of duration D’. Consequently, to convert this hydrograph whose volume is D’/D into a unit hydrograph of duration D’, its ordinates must be normalized by multiplying them by D/D’. The resulting ordinates represent a unit hydrograph associated with an effective rainfall of duration D’
- A hydrologic system (a basin) is said to be a linear system if the relationship between storage, inflow, and outflow is such that it leads to a linear differential equation.
2.5.1 Synthetic Unit Hydrograph
The conservation Service (SCS) has performed a synthesis of an excellent variety of unit hydrographs for watercourse basins of assorted sizes situated in numerous regions of the USA. So as to check these unit hydrographs their ordinates and abscissas were normalized. Were divided the ordinates by the height discharges up whereas the abscissas were divided by the time to peak tp. What is more, the non-dimensional ordinates and abscissas were averaged getting the non-dimensional artificial hydrograph (SUH), the abscissas t/t p
The following variables conferred within the graph area unit defined:
- Duration of effective downfall D
- The concentration time t c between the tip of effective downfall and also the grammatical relation purpose of the hydrograph;
- The lag time t1 between the mid-point of the effective downfall and also the time of the height discharge (approx. t1 = 0.66 t c);
- The increase time of the hydrograph t p;
- The decrease time of the hydrograph t r;
- The base time of the hydrograph t b.
This triangular SCS-synthetic hydrograph is outlined by the parameters up (maximum discharge) and tp. Within the triangular hydrograph thirty seven.5% of the quantity of the flood wave is found simply before the height, thence t p/t b = zero.375
2.5.2 Instantaneous Unit Hydrograph
- The effects of urbanization of a basin on the runoff are investigated within the past by the utilization of linear abstract models during which the wait seems as a crucial parameter. However, during this approach the consequences of noise within the information, of rate, of errors thanks to the shortage of synchronization between the effective downfall and runoff on the fast unit hydrograph do not become without delay apparent.
- A case during which the accumulative effects of those factors area unit predominant is conferred as associate degree example of the attainable difficulties which could be encountered within the analysis of urban hydrological information by the unit hydrograph methodology.
- The disadvantages of relating the height discharge, the time to peak discharge and also the wait to the physiographic characteristics alone are mentioned.
- Various regression relationships that involve storm characteristics at the side of the physiographic characteristics to estimate the height discharge, time to peak discharge and wait are conferred.
- The fast unit hydrograph is outlined as a unit hydrograph made by an efficient downfall of one metric linear unit associate degreed having an minute reference length (in alternative words the length tends towards zero).
- In terms of the systematic conception this implies that the fast unit hydrograph represents the response of the structure to a direct impulse. Of course, this can be solely a theoretical conception and can't be realized in actual catchments, however it's helpful because the IUH are often analytically computed and, on the idea of the "S" curve exact unit hydrograph of any reference length could also be derived from it. Moreover, the IUH are often associated with the structure geophysics.
Key takeaways
- Unit hydrograph
A unit hydrograph is defined as they hydrograph of direct runoff resulting from one unit depth (1 cm) of rainfall excess occurring uniformly over the basin and at a uniform rate for a specified duration (D hours). OR
- S curve hydrograph
An S-hydrograph represents the response of the basin to an effective rainfall event of infinite duration. Assume that a UH of duration D is known and that a UH for the same basin but of duration D’ is desired. The first step is to determine the S-curve hydrograph by adding a series of (known) UH’s of duration D, each lagged by a time interval D. The resulting superposition represents the runoff resulting from a continuous rainfall excess of intensity 1/D.
- Synthetic unit hydrograph
The conservation Service (SCS) has performed a synthesis of an excellent variety of unit hydrographs for watercourse basins of assorted sizes situated in numerous regions of the USA. So as to check these unit hydrographs their ordinates and abscissas were normalized. Were divided the ordinates by the height discharges up whereas the abscissas were divided by the time to peak tp. What is more, the non-dimensional ordinates and abscissas were averaged getting the non-dimensional artificial hydrograph (SUH), the abscissas t/t p
- Instantaneous unit hydrograph
The effects of urbanization of a basin on the runoff are investigated within the past by the utilization of linear abstract models during which the wait seems as a crucial parameter. However, during this approach the consequences of noise within the information, of rate, of errors thanks to the shortage of synchronization between the effective downfall and runoff on the fast unit hydrograph do not become without delay apparent.
References
- Techmax
- Groundwater Hydrology by Todd D K Wiley
- Irrigation Theory and Practice by Michael A M Vikas Publication House
- Engineering Hydrology by Ojha Oxford University