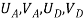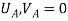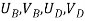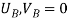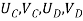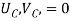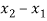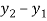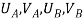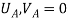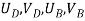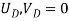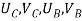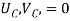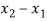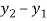Unit - 5

Analysis of structures

5.1 Analysis of structures: Truss elements

• Definition: A truss is a structure that consists of

1)     All straight members

2)     Connected together with pin joints

3)     Connected only at the ends of the members

4)     And all external forces (loads & reactions) must be applied only at the joints.

• The analysis of trusses is usually based on the following simplifying assumptions:

1)     The centroidal axis of each member coincides with the line connecting the centers of the adjacent members and the members only carry axial force.

2)     All members are connected only at their ends by frictionless hinges in plane trusses.

• Trusses Using FEA In this section, we will apply basic finite element techniques to solve general two dimensional truss problems. The technique is a little more complex than that originally used to solve truss problems, but it allows us to solve problems involving statically indeterminate structures.

5.2 Analysis of truss problems by direct stiffness method

Stiffness matrix of a truss element

• The truss may be statically determinate or indeterminate. All members are subjected to only direct stresses (tensile or compressive). Joint displacements are selected as unknown variables.
• Since there is no bending of the members we have to ensure only displacement continuity (C continuity) and there is no need to worry about slope continuity (C continuity).
• Here we select two noded bar element for the formulation of stiffness matrix of truss element. Since the members are subjected to only axial forces, the displacements are only in the axial directions of the members.
• Therefore, the nodal displacement vector for the bar element is

                                                     {}=     

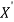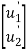
Where, 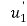and 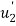are the displacements in axial direction of the element. The stiffness matrix of a bar element is

[]=

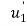
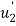
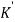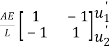
Problems-

Example 1-

Analyze the truss as shown in fig. Cross sectional area of members are AB= 1000 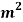, BC=800 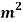,CA= 800 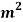take E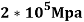

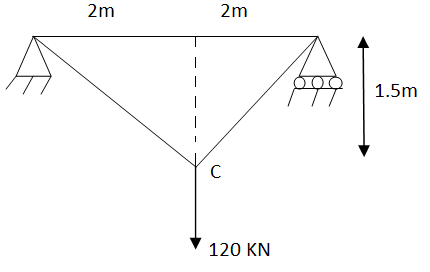
Ans-

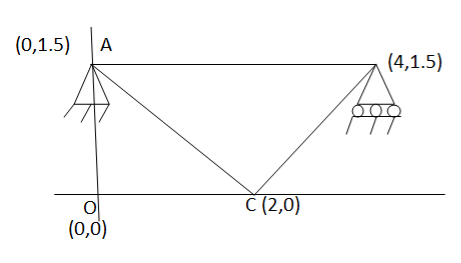
Step-1 degrees of freedom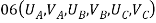

Discretization –

Elements	Nodes	Displacements mm	Boundary conditions
1	AB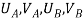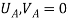
2	BC		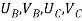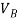=0
3	CA		-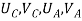

Assume x-axis horizontal through point (& vertical through point A). The co-ordinates of node A(0,1.5) , B(4,1.5) & C(2,0) . Take E in Gpa.

Member		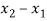	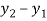L	l	m	AE/l (KN/mm)
AB	4	0	4	1	0	50
BC	-2	-1.5	2.5	-0.8	-0.6	64
CA	-2	1.5	2.5	-0.8	0.6	64

Step-2 element stiffness matrices

Stiffness matrix of element AB.

Stiffness matrix of element BC

Stiffness matrix of element CA

Step 3- global stiffness matrix

Total Dof are 06, size of stiffness matrix 6*6

Step -4 reduced stiffness matrix

Since 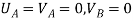eliminate corresponding rows & columns from global stiffness matrix

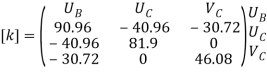
Step -5 equation of equilibrium

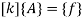
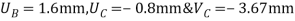
Example -2

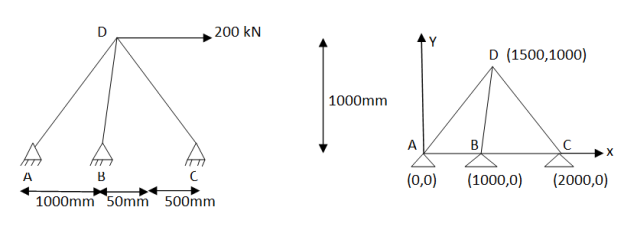
Figure shows a plane, truss with three members cross- sectional area of all members 500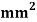 young modulus is 200 KN/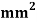. Determine deflection at loaded joint .

Solution –

Step 1 – degree of freedom ;- 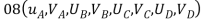Discretization Element Nodes Displacement (mm) Boundary cond 1 AD 2 BD 3 CD   Assume origin support A(0,0). The co-ordinates of other nodes&  B(1000,0), C(2000,0) and D(1500,1000) Member L l m AE/L (KN/M) AD 1500 1000 1802.8 0.832 0.555 88.75 BD 500 1000 1118 0.447 0.894 143.112 CD -500 1000 1118 -0.477 0.894 143.112   Step -2 element stiffness matrices Stiffness matrix of element AD   Step – 3 equations of equilibrium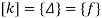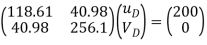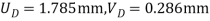

Example 3 –

For the truss as shown in fig. Using finite element method, determines deflections at loaded joints. The joint B is subjected to 50 KN horizontal force towards left & 80 KN force vertically downward. Take cross sectional area of all the members 1000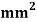 young modulus is 200 Gpa.

Ans-

Step -1 degree of freedom (06) 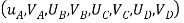Discretization Element Nodes Displacement (mm) Boundary cond 1 AB 2 DB 3 CB   Assume origin point B. The co-ordinates points are 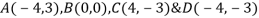Members L l m AE/L (kN/mm) AB 4000 -3000 5000 0.8 -0.6 40 DB 4000 3000 5000 0.8 0.6 40 CB -4000 30000 5000 -0.8 0.6 40   Step -2  stiffness  matrix of element AB . Stiffness matrix at element DB.   Step 3- reduced stiffness matrix 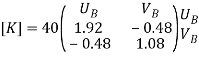  Step 4- equation of equilibrium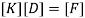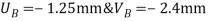

5.3 Analysis of frames and different problems

Steps for the solution of Indeterminate plane frames using finite element method:

1. Divide the frame into number of elements (Take one member as one element)

2. Identify total degrees of freedom (Three D.O.F. At each node, two displacements and rotation)

3. Determine stiffness matrices of all elements ([K]1, [K]2……)

4. Assemble the global stiffness matrix [K] 

5. Impose the boundary conditions and determine reduced stiffness matrix.

6. Determine element nodal load vector [q] (Restrained structure)

7. Determine equivalent load vector[f]

8. Apply equation of equilibrium [K]{∆}={f}, and determine unknown joint displacements.

9. Apply equation [K]{∆}+[q]={f} to determine reactions and moments

Problems-

Example 1-

Analysis the portal frame as shown in fig. Using finite element methos take EI constant. Neglect axial deformation

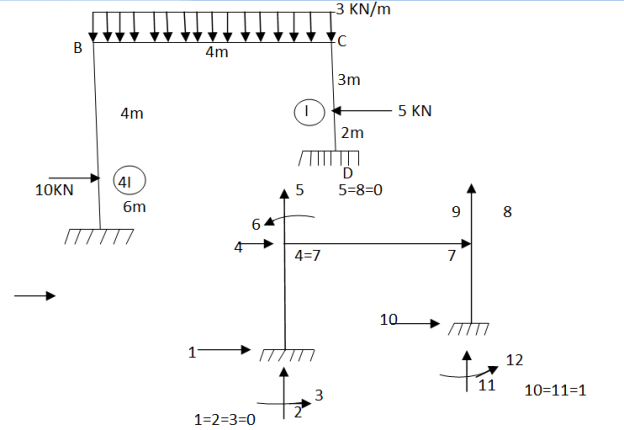
Step -1 total DoF =12 (three DOf at each node, two displacement & one rotation) No. Of elements 03 (AB,BC,CD) Discretization Element Nodes Displacement Boundary conditions 1 AB 1,2,3,4,5,,6, 1=2=3=zero 2 BC 4,5,6,7,8,9 5=8=zero,4=7 3 DC 10,11,12,7,8,9 10=11=12=zero   Step 2- element stiffness matrix Element stiffness matrix from AB (column member) Imposing boundary conditions 5=8=0 Element stiffness matrix for DC Imposing boundary conditions 10=12=0   Step -3 reduced stiffness matrix Since horizontal sway at B& C are same (4=7) we can modify the above stiffness matrix as     Step -4 element nodal load vector 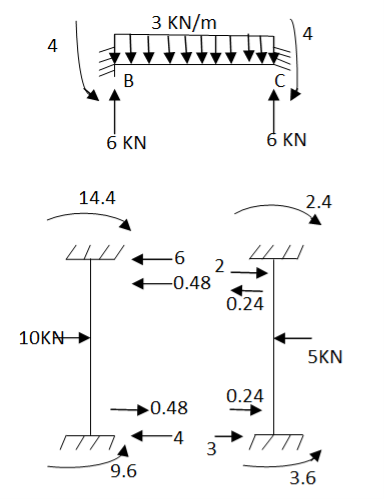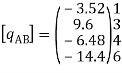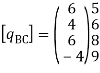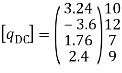Reduced element nodal load vector 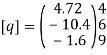  Step -5 equivalent load vector {f}= {q}+ joint forces 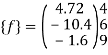  Step -6 equation of equilibrium 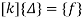 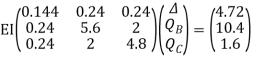 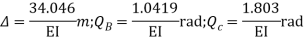Step -7 moment calculations 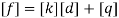Member AB 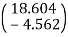= Member BC 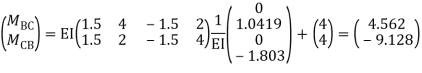Member DC

Example – 2

Analyze the rigid frame by using finite element method. Take EI constant . Neglect axial deformation

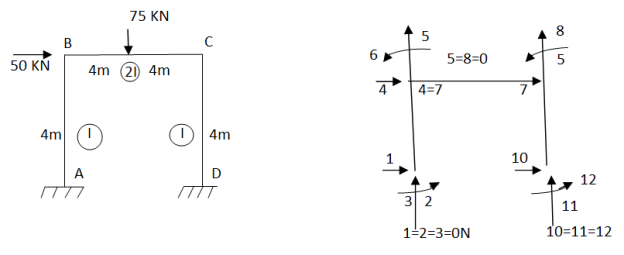
Step -1 total DOf =12 (three dof at each node , two displacements & one rotation) Element Nodes Displacement Boundary conditions 1 AB 1,2,3,4,5,,6, 1=2=3=zero 2 BC 4,5,6,7,8,9 5=8=zero,4=7 3 DC 10,11,12,7,8,9 10=11=12=zero   Step -2 element stiffness matrix for column AB Element stiffness matrix of beam Bc Element stiffnes matrix of beam DC.   Imposing boundary condition 1=2=3=5=8=10=11=12=0   Step -3 reduced stiffness matrix Since horizontal sway at B &C are same (4=7) , we can modify the above stiffness matrix as   Step -4 element nodal load vector 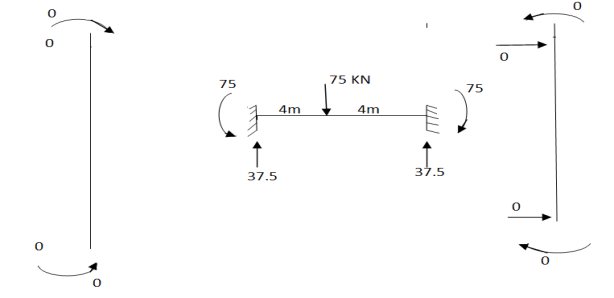 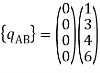  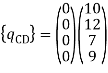                             Reduced element nodal load vector 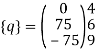  Step -5 equivalent load vector 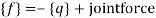 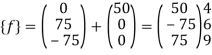 Step -6 equation of equilibrium  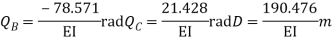 Step -7 moment calculations 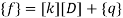Member AB 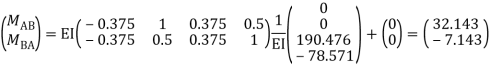Member BC Member DC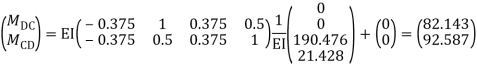

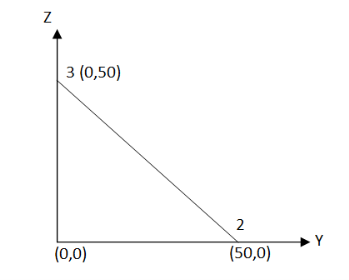
5.4 Different Axi-symmetric truss problems

Example 1

For the axisymmetric element shown in figure, determine the element stresses

Let E=210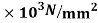

Poisson’s Ratio=0.25

The total displacements are

u1=0.05mm ;    W1=0.03mm

u2=0.02mm;  W2=0.02mm

u3=0mm;W3=0mm

To Find Element Stresses & Stiffness Matrix

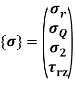
Solution:

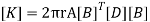
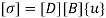
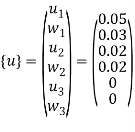
We know that

&

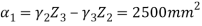
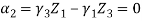
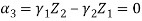
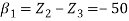
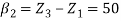
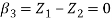
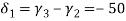
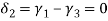
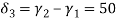
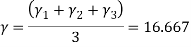
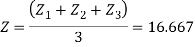
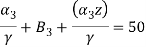
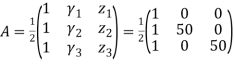=1250mm

Substitute all this values in {B}

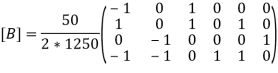
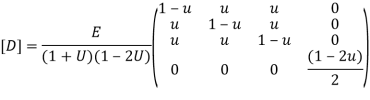
                                         Put =E =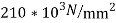

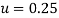
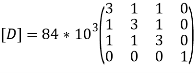
We know that stiffness matrix

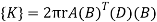
Note ; matrix form [k]= (6*6)

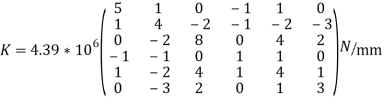
To find stresses

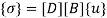
Note – matrix form = 4*1

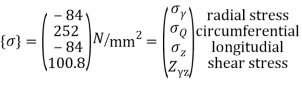
Example 2

A long hollow cylinder of inside diameter 80mm & outside diameter 120mm is firmly filled in a hole of another rigid cylinder over it full length as shown in fig. The cylinder is then subjected to an internal pressure of 2 MPa. By using two elements on the 10mm length shown . Find the displacement at the inner radius . Take E=200 Gpa ,u=0.3

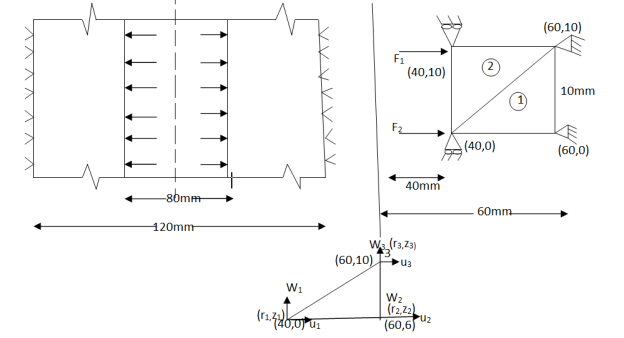
Solution -

Stiffness matrix for element 1

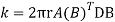
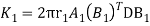
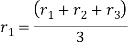
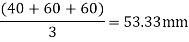
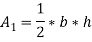
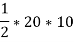
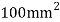
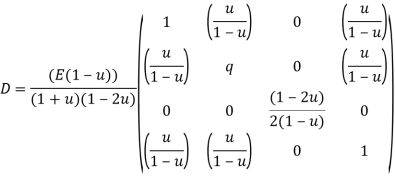
For the both elements 

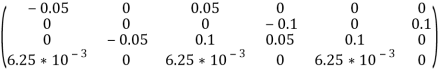
The stiffness matrices for element

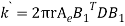
References-

(1)  Finite Element Analysis -C.S. Krishnanmoorthy, Tata McGraw Hill Publishing Co. Ltd, New Delhi,

(2)  The Finite Element method -ZIENKIEWICZ.O.C.Tata McGraw Hill Pub. New Delhi, 2000

(3)  Finite Element Methods by C R Alaval , PHI

(4)  Finite Elements in Engineering:- Chandrupatta, et. AI. Prentice Hall of India Pvt. Ltd.,