Unit - 5
Virtual Work and Energy Method
In general, the definitions of the work of a force and a couple can be presented in terms of the actual movements which are expressed by differential displacements having values of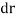 
and 
.
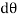Consider now an imaginary or virtual movement of a body in static equilibrium, which indicates a displacement or rotation that is assumed and does not actually exist. This displacement is called as virtual displacement.
Virtual displacement is the displacement the force or couple would make on a body if the body was not in the static equilibrium or its motion would not be constrained.
These movements are first-order differential quantities and will be denoted by the symbols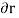 
and 
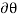(delta r and delta 
), respectively.
The virtual work done by a force having a virtual displacement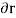 
is
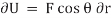
Similarly, when a couple undergoes a virtual rotation 
in the plane of the couple forces, the virtual work is
Consider a ball that rests on a floor. If there was no floor below the ball, then the ball would have been displaced due to its own weight. Then this imaginary displacement of the ball is nothing but the virtual displacement.
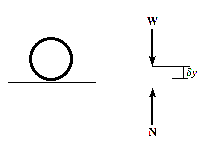
The principle of virtual work states that if a body is in equilibrium, then the algebraic sum of the virtual work done by all the forces and couple moments acting on the body, is zero for any virtual displacement of the body.
Thus,
For example, consider the free-body diagram of the particle (ball) that rests on the floor, Fig. Below. If we “imagine” the ball to be displaced downwards a virtual amount 
then the weight does positive virtual work 
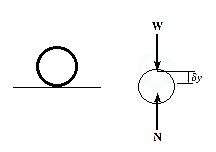
, and the normal force does negative virtual work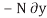 
, For equilibrium the total virtual work must be zero, so that
Since, 
,
Then,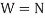 
, as required by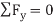 
As seen from the above example, no added advantage is gained by solving particle and rigid-body equilibrium problems using the principle of virtual work. This is because for each application of the virtual-work equation, the virtual displacement, common to every term, factors out, leaving an equation that could have been obtained in a more direct manner by simply applying an equation of equilibrium.
In a similar manner, as that of particle, we can also apply the virtual-work equation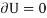 
to a rigid body subjected to a coplanar force system.
Here, separate virtual translations in the x and y directions and a virtual rotation about an axis perpendicular to the x–y plane that passes through an arbitrary point O, will correspond to the three equilibrium equations,
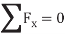
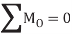
When writing these equations, it is not necessary to include the work done by the internal forces acting within the body since a rigid body does not deform when subjected to an external loading, and furthermore, when the body moves through a virtual displacement, the internal forces occur in equal but opposite collinear pairs, so that the corresponding work done by each pair of forces will cancel.
To demonstrate an application, consider the simply supported beam in Fig(a). When the beam is given a virtual rotation about point B, Fig(b), the only forces that do work are P and Ay
Since,
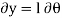
And
The virtual work equation for this case is
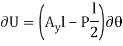
Since,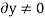 
,
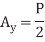
Excluding 
, notice that the terms in parentheses actually represent the application of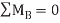 
The method of virtual work is particularly effective for solving equilibrium problems that involve a system of several connected rigid bodies, such as the ones shown in Figure below.
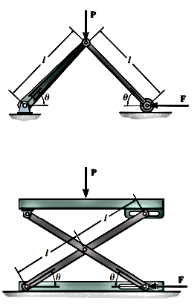
Each of these systems is said to have only one degree of freedom since the arrangement of the links can be completely specified using only one coordinate. In other words, with this single coordinate and the length of the members, we can locate the position of the forces F and P.
Degree of freedom is defined as the total number of independent coordinates required to specify the complete location of every member of the structure.
Degree of freedom is also defined as number of independent motions a rigid body can have.
Consider a rigid body which is unconstrained in a 3D space have following independent motions:
- Translational motion along the three axes
- Rotational motion about its axes
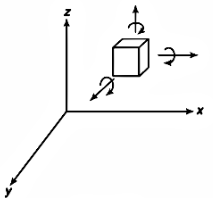
It means an unconstrained rigid body in 3D space possesses 6 degree of freedom.
Now, if a rigid body is constrained to rotate in all axes, the body will have 3 degree of freedom.
If the body is restricted to have motion in a x-y plane. Then the motion the body will have is
- Translation motion in x and y axes.
- Rotation motion about z-axis.
Hence, the total maximum degree of freedom a rigid body in planar motion have is 3.
Mathematically, degree of freedom of a body in 3D space is given as,
And, degree of freedom of a body in plane motion is given as,
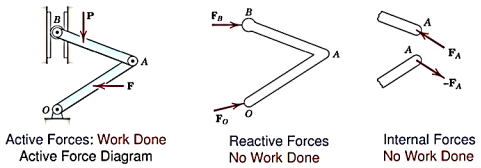
There are three types of forces that acts on a rigid body.
- Active forces
The forces that are responsible for work to be done are called as active forces.
- External forces – applied forces, gravitational forces
- Internal forces – spring forces, viscous forces
2. Reactive forces
The forces by the rigid body as a reaction of active forces are called as reactive forces. These are not responsible for the work
3. Internal forces
The forces in the rigid body are internal forces. These forces also don’t do any work
While solving the problems by the principle of virtual work, Virtual displacements are to be given carefully so that the active forces are only the known forces and the forces we are interested in obtaining.
Hence, Active force diagram are drawn which is similar to FBD.
Active force diagram (AFD) is the diagram that contains only the active forces acting on a system or a body.
Difference between FBD and AFD is explained in diagrams below.
So far, the principle of virtual work was discussed for “ideal” systems.
If significant friction is present in the system (“Real” systems), work done by the external active forces (input work) will be opposed by the work done by the friction forces.
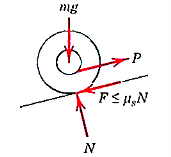
Consider a block is on a flat surface acting with force P as shown in figure below.
Let 
be the virtual displacement and 
is the coefficient of kinetic friction.
Then the work done by kinetic friction force is
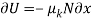
Where, N is the normal force, N = mg
Now, consider another example wheel rolling on an elevated surface as shown in figure below.
Here, during rolling of a wheel, if the wheel does not slip as it rolls, the static friction force does no work.
The mechanical efficiency of a machine is defined as the ratio of the output of useful power produced by the machine to the input of power supplied to the machine. Hence,
If energy supplied to the machine occurs during the same time interval at which it is drawn, then the efficiency may also be expressed in terms of the ratio
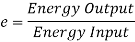
Since machines consist of a series of moving parts, frictional forces will always be developed within the machine, and as a result, extra energy or power is needed to overcome these forces. Consequently, power output will be less than power input and so the efficiency of a machine is always less than 1.
For simple machines with SDOF & which operates in uniform manner, mechanical efficiency can also be determined using the method of Virtual Work.
Consider a system shown in figure.
For the virtual displacement ∂s, output Work is the work that is necessary to elevate the block.
Hence,
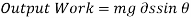
Input work is given as,
Hence, efficiency is
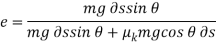
Conservative Forces
If the work of a force only depends upon its initial and final positions, and is independent of the path it travels, then the force is referred to as a conservative force. The weight of a body and the force of a spring are two examples of conservative forces.
Weight:
Consider a block of weight that travels along the path in Figure.
When it is displaced up the path by an amount, then the work is
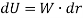
OR
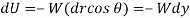
Shown in figure below.
In this case, the work is negative since acts in the opposite sense of. Thus, if the block moves from to, through the vertical displacement, the work is
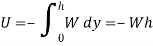
The weight of a body is therefore a conservative force, since the work done by the weight depends only on the vertical displacement of the body, and is independent of the path along which the body travels.
Spring Force:
Now consider the linearly elastic spring in Figure, which undergoes a displacement ds.
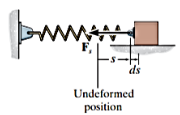
The work done by the spring force on the block is
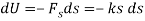
The work is negative because 
acts in the opposite sense to that of ds. Thus, the work of 
when the block is displaced from 
to 
is
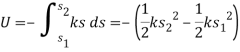
Here the work depends only on the spring’s initial and final positions, 
and 
, measured from the spring’s unstretched position. Since this result is independent of the path taken by the block as it moves, then a spring force is also a conservative force.
Friction:
In contrast to a conservative force, consider the force of friction exerted on a sliding body by a fixed surface. The work done by the frictional force depends on the path; the longer the path, the greater the work. Consequently, frictional forces are nonconservative, and most of the work done by them is dissipated from the body in the form of heat.
Potential Energy
When a conservative force acts on a body, it gives the body the capacity to do work. This capacity, measured as potential energy, depends on the location of the body relative to a fixed reference position or datum.
Gravitational Potential Energy:
If a body is located a distance y above a fixed horizontal reference or datum as in Figure, the weight of the body has positive gravitational potential energy 
since W has the capacity of doing positive work when the body is moved back down to the datum.
Likewise, if the body is located a distance y below the datum, is negative since the weight does negative work when the body is moved back up to the datum. At the datum,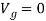 
Measuring y as positive upward, the gravitational potential energy of the body’s weight W is therefore
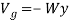
Elastic Potential Energy:
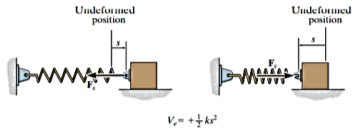
When a spring is either elongated or compressed by an amount s from its unstretched position (the datum), the energy stored in the spring is called elastic potential energy. It is determined from
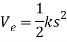
This energy is always a positive quantity since the spring force acting on the attached body does positive work on the body as the force returns the body to the spring’s unstretched position.
Potential Function:
In the general case, if a body is subjected to both gravitational and elastic forces, the potential energy or potential function V of the body can be expressed as the algebraic sum.
Where measurement of V depends on the location of the body with respect to a selected datum.
If a system of frictionless connected rigid bodies has a single degree of freedom, such that its vertical position from the datum is defined by the coordinate q, then the potential function for the system can be expressed as
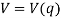
The work done by all the weight and spring forces acting on the system in moving it from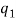 
to 
, is measured by the difference in V, i.e.,
Now, if a frictionless connected system has one degree of freedom, and its position is defined by the coordinate q, then if it displaces from q to q + dq,
Then the above equation becomes,
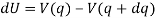
OR
If the system is in equilibrium and undergoes a virtual displacement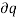 
, rather than an actual displacement dq, then the above equation becomes
However, the principle of virtual work requires that
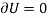
Therefore,
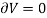
Hence, we can write,
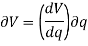
Since,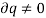 
,
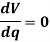
This is the energy equation for equilibrium.
Hence, when a frictionless connected system of rigid bodies is in equilibrium, the first derivative of its potential function is zero.
This energy equation can be applied to a mass under gravitational force or a spring either elongated or compressed or a system of both mass and spring.
Consider a spring block system as shown in figure below
The potential function for a system consisting of a block of weight W supported by a spring, as in Figure, can be expressed in terms of the coordinate measured from a fixed datum located at the unstretched length of the spring. Here
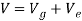
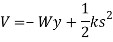
Using energy equation, we can determine the equilibrium position for the spring and block.
We have,
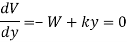
Hence, the equilibrium position is
The potential function V of a system can also be used to investigate the stability of the equilibrium configuration, which is classified as stable, neutral, or unstable.
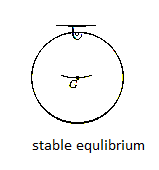
Stable Equilibrium: A system is said to be stable if a system has a tendency to return to its original position when a small displacement is given to the system. The potential energy of the system in this case is at its minimum. A simple example is shown in Fig. Below. When the disk is given a small displacement, its center of gravity G will always move (rotate) back to its equilibrium position, which is at the lowest point of its path. This is where the potential energy of the disk is at its minimum.
The graph represents stable equilibrium for one degree of freedom system.
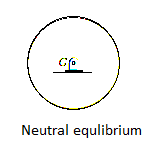
Neutral Equilibrium: A system is said to be in neutral equilibrium if the system still remains in equilibrium when the system is given a small displacement away from its original position. In this case, the potential energy of the system is constant. Neutral equilibrium is shown in Fig. Below, where a disk is pinned at G. Each time the disk is rotated, a new equilibrium position is established and the potential energy remains unchanged.
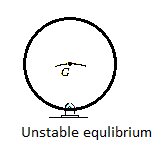
Unstable Equilibrium: A system is said to be unstable if it has a tendency to be displaced further away from its original equilibrium position when it is given a small displacement. The potential energy of the system in this case is a maximum. An unstable equilibrium position of the disk is shown in Fig. Below. Here the disk will rotate away from its equilibrium position when its center of gravity is slightly displaced. At this highest point, its potential energy is at a maximum.
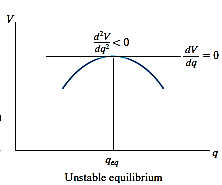
Stability in one degree of freedom system:
If a system has only one degree of freedom, and its position is defined by the coordinate q, then the potential function V for the system in terms of q can be plotted.
Provided the system is in equilibrium, then dV/dq, which represents the slope of this function, must be equal to zero. An investigation of stability at the equilibrium configuration therefore requires that the second derivative of the potential function be evaluated.
If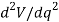 
is greater than zero, the potential energy of the system will be a minimum. This indicates that the equilibrium configuration is stable.
Hence, for stable equilibrium,
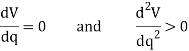
If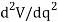 
is less than zero, the potential energy of the system will be a maximum. This indicates that the equilibrium configuration is unstable.
Hence, for unstable equilibrium,
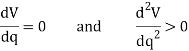
Finally, if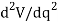 
is equal to zero, it will be necessary to investigate the higher order derivatives to determine the stability. The equilibrium configuration will be stable if the first non-zero derivative is of an even order and it is positive. Likewise, the equilibrium will be unstable if this first non-zero derivative is odd or if it is even and negative. If all the higher order derivatives are zero, the system is said to be in neutral equilibrium.
Hence, for neutral equilibrium,
This condition occurs only if the potential-energy function for the system is constant at or around the neighborhood of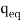 
.
References:
1. Irving H. Shames (2006), Engineering Mechanics, 4th Edition, Prentice Hall
2. F. P. Beer and E. R. Johnston (2011), Vector Mechanics for Engineers, Vol I - Statics, Vol II, – Dynamics, 9th Ed, Tata McGraw Hill
3. R. C. Hibbler (2006), Engineering Mechanics: Principles of Statics and Dynamics, Pearson Press.
4. Andy Ruina and Rudra Pratap (2011), Introduction to Statics and Dynamics, Oxford University Press
5. Shanes and Rao (2006), Engineering Mechanics, Pearson Education
