Unit - 1
Basic Concepts and Definition
Key takeaways
Fluid is defined as a substance that progressively deforms when subjected to shear stress of any size.
When solid foods such as iron or other metals are subjected to shear pressure, they will initially be disabled (usually the smallest factor), but they will not continue to degenerate (flow).
ρ = m/ v
Measurement of density
Homogeneous material
Heterogeneous material
m = integration v ρ(r)dV
Non compacted material
Key takeaways
Quantity (precisely, the size of the volume of a volume; also known as a specific weight), of an object whose weight is the volume of the unit.
The symbol most commonly used for congestion is ρ (the capital letter of the Greek word rho), although the Latin letter D may also be used. Statistically, quantity is defined as the quantity divided by volume
ρ = m/ v
Definition
Gamma = ρ g
Key takeaways
The specific weight, γ, of a story is defined as the product of its plurality, ρ, and the common gravitational force, g:
Gamma = ρ g
Uses
Examples
Q.1 Density of liquid is 850 kg/m³. Determine relative density and weight density of the liquid. With reason state whether the liquid will float on water or not
Soln.:
Gives:
p= 850kg/m'.
P. 1000kg/m (standard value)
To find: Relative density, weight density
Relative density

Weight density
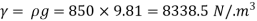
The liquid will float on water because weight density of liquid is less than water.
Q.2 On a certain planet a correctly calibrated spring balance shows the weight of a body s 12 N, the mass of which is 4.893 kg. Find the value of gravity on this planet.
Soln.:
Given:
Weight W= 12 N.
Mass m = 4.893 kg
Weight = Mass x acceleration


Acceleration due to gravity on a certain planet is 2.45 m/sec.
Q.3 What is the specific volume of material with specific gravity 0.87
Soln.:
Given:
Specific gravity=0.5,
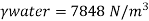
To find: Specific volume.
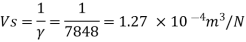
Q.4 The specific volume of a certain gas is 0.7m/kg Determine its specific weight and mass density.
Soln.:
Given:
Specific volume =0.7
To find: Mass density, specific weight
Mass density (p)
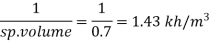
Specific weight (Y)
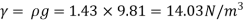
Q.5 Calculate the specific weight, density, specific volume and relative duty of oil which 7 N per liter.
Soln.:
Given:
Weight W=7N,
Volume V= 1 litre = 10^-3 'm^3
To find:
Specific weight,
Specific volume,
Relative density
Specific weight Y
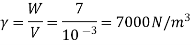
Density
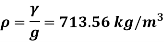
Specific volume (Vs)
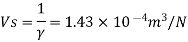
Relative density
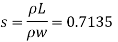
Q.6 2 liter of petrol weighs 14N. Calculate the specific weight, density, specific volume and specific gravity of petrol with respect to water.
Soln.:
Given: V=2 liter = 2 x 10-3m,
W=14N
To find:

Specific weight = Mass density x Acceleration due to gravity
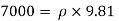

2. Specific volume (V)
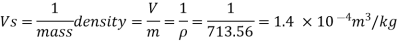
3. Specific gravity (S)
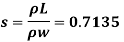
Q. 7 A 400 ml of certain liquid weight 9N calculate the weight density and specific gravity of the liquid.
Soln.:
Given:
Volume V= 400 ml-0.4 L=0.4/1000=4x10^-4 m^3
Weight W=9N
To find: Weight density, specific gravity
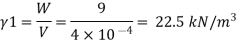
2. Specific gravity
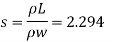
Key takeaways
The relative quantity or gravitational force is a measure of the size (volume of a unit volume) of an object in the quantity of a given object.
The gravitational force of the liquid is almost always measured in relation to the water obtained (at 4 ° C or 39.2 ° F); for gases, the reference is air at room temperature (20 ° C or 68 ° F). The term "relative congestion" is often popular in scientific practice.
Dynamic Viscosity
Absolute viscosity - the coefficient of total viscosity - is the measure of internal resistance. Dynamic (absolute) viscosity is the tangential force at each unit area required to move one horizontal plane in relation to another plane - by unit velocity - while maintaining unit distance outside the fluid.
Shave pressure between layers of fluid in straight lines can be defined by Newtonian fluid as
Liquid - viscosity and velocity profile
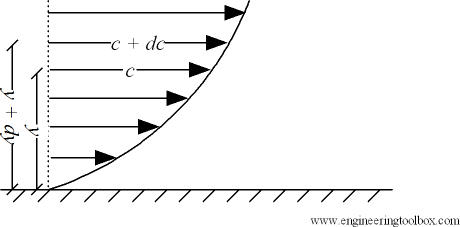
Fig no 1 Dynamic and kinematic viscosity
Shear depression can be shown
τ = μ dc / dy
= μγ. ........ (1)
Where
τ = cutting pressure on liquid (N / m2)
μ = strong viscosity of liquid (N s / m2)
dc = unit velocity (m / s)
dy = unit distance between layers (m)
γ = dc / dy = shear rate (s-1)
Equation (1) is known as the Newtons Law of Friction.
(1) Can be rearranged to reflect Dynamic viscosity as
μ = τ dy / dc
= τ / γ. .......... . (1b)
1 Pa s = 1 N s / m2 = 1 kg / (m s) = 0.67197 lbm / (ft s) = 0.67197 slug / (ft s) = 0.02089 lbf s / ft2
1 poise = 1 dyne s / cm2 = 1 g / (cm s) = 1/10 Pa s = 1/10 N s / m2
1 P = 100 cP
1 cP = 0.01 poise = 0.01 gram per cm second = 0.001 second Pascal = 1 milliPascal second = 0.001 N s / m2
20.2oC (68.4oF) liquids have a perfect viscosity of one - 1 –centiPoise.
Kinematic Viscosity
Kinematic viscosity is a measure of the total viscosity - (or intensity) of a quantity - the amount of non-energy. Kinematic viscosity can be obtained by dividing the total viscosity of the liquid by the amount of fluid mass
ν = μ / ρ ..................(2)
Where
ν = kinematic viscosity (m2 / s)
μ = full or strong viscosity (N s / m2)
ρ = density (kg / m3)
In the SI-system the unit of kinematic viscosity theory is m2 / s - or the most commonly used Stoke (St) where
Stoke comes from the CGS unit program (Centimeter Gram Second Second).
As the Stoke unit is usually divided by 100 into smaller units centiStoke (cSt) - there
The gravitational force of 20.2oC (68.4oF) is almost the same, and the kinematic viscosity of 20.2oC (68.4oF) water is designed to operate 1.0 mm2 / s (cStokes). The most precise water viscosity at 20.2oC (68.4oF) is 1.0038 mm2 / s (cSt).
Conversion from full viscosity to kinematic in Imperial units can be shown as
ν = 6.7197 10-4 μ / γ. .................... (2a)
Where
ν = kinematic viscosity (ft2 / s)
μ = full or strong viscosity (cP)
γ = specific weight (lb / ft3)
Examples:
Q.1 A plate 0.02 mm distance from a fixed plate, moves at 60 cmvs and requires a force of 3 N/m² to maintain this speed. Determine the fluid viscosity between the plates.
Soln.:
Given: Distance between plates
dy= 0.02 mm = 0.02 x 10-3 m
Velocity of upper plate u 60 cm/s 0.6 m/s
Change in velocity du=u-0-0.6 m/s.
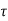 = Force per unit Area = 3 N/m²
= Force per unit Area = 3 N/m²
To find: Viscosity
Using Newton's law of viscosity
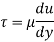
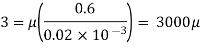
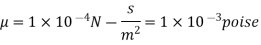
The fluid viscosity between the plates is 1 x 10-3 poise,
Q.2 A flat plate of area 2.5 x 10 mm² is pulled with a speed of 0.4m's relative to another plate locate at a distance of 0.15mm from it. Find the force and power required to maintain this speed, if the fluid separating them is having viscosity as 1 poise
Soln.:
Given:
A=2.5 x 10 mm²=2.5m²,
du= 0.4m/s dy-0.15mm = 0.15 x 10 m,
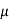 =1 poise = 0.1N-s/m
=1 poise = 0.1N-s/m
To find: Force, power
Using Newton's law of viscosity:
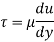
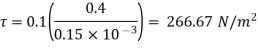
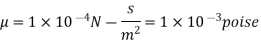
As we known 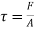

Power required to move the plate at speed 0.4 m/s
= Force x Velocity = 666.67 x 0.4 N-m/
1 N-m/s = 1 Watt
P = 266.67 Watt
Power required moving the plate is 266.67 Watt.
Q.3 The space between two square flat parallel plates is filled with oil. Each side of the plate is 720 mm. The thickness of the oil film is 15 mm. The upper plate, which moves at 3 ms requires a force of 120 N to maintain the speed. May 2016. 6 Marks
Determine:
(1) The dynamic viscosity of oil.
(2) The kinematic viscosity of oil if the specific gravity of oil is 0.95
Solution:
Square plate of side, a = 720 mm=0.72 m
Thickness of oil film, t = 15 mm= 15 x 10
Velocity of plate v= du= 3m/s
Force F= 120 N
Specific gravity s= 0.95
To find 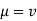
Mass density,
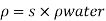
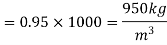
Area of plate,
A= 0.72x0.72 = 0. 5184 m²
Using Newton's law viscosity
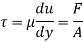
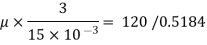
Dynamic viscosity 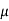 = 1.157 N/m²
= 1.157 N/m²
Kinematic viscosity, v 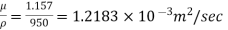
Q. 4 A body with gravity force of 500 N with a flat surface area 0.2 m slides down a lubricated inclined plane making a 30° angle with the horizontal. For viscosity of 0.1 kg s/m and body speed of 1 m/s. Determine the lubricant film thickness
Soln.:
Given:
Area A = 0.2 m²
Weight of late W = 500 N
Velocity of plate u = 1 m/sec 0.1kg /m²=0.1 x 9.81 N.s/m² = 0.981 N-s/m²
To find: Thickness of film.
Component of W along the plate W sin 8= 500 sin 30= 250 N
Shear force on the bottom surface of the plate
F = 250N


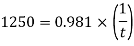
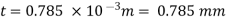
The lubricant film thickness is 0.785 mm
Q.5 A rectangular plate 1.2 m x 0.4 m. weighting 970N slides down a 45° inclined surface at a uniform velocity of 2.25 m/s. If the 2mm gap between the plate and the inclined surface is filled with oil, determine the viscosity of oil.
Soln.:
Given:
Area A = 12x04 0.48 m²
Weight of plate W =970 N
Velocity of plate u = 2.25 m/sec
Thickness of film t = dy = 2 mm = 2 x 10³ m
To find: Viscosity
Component of W along the plate= W sin 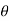
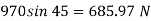
Shear force on the bottom surface of the plate
F= 685.89 N

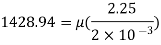
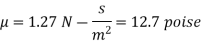
The viscosity of the liquid is 12.7 poise.
Key takeaways
Dynamic viscosity
Absolute viscosity - the coefficient of total viscosity - is the measure of internal resistance. Dynamic (absolute) viscosity is the tangential force at each unit area required to move one horizontal plane in relation to another plane - by unit velocity - while maintaining unit distance outside the fluid.
Kinematic viscosity
Kinematic viscosity is a measure of the total viscosity - (or intensity) of a quantity - the amount of non-energy. Kinematic viscosity can be obtained by dividing the total viscosity of the liquid by the amount of fluid mass
The following formula provided by Poiseuille shows the dependence of the viscosity of the liquid on the heat-

where,  Viscosity of the liquid at
Viscosity of the liquid at 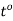 C in poise
C in poise
 Viscosity of the liquid at
Viscosity of the liquid at  C in poise
C in poise
and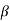 are constant characteristics of the liquid.
are constant characteristics of the liquid.
For water, 
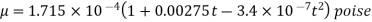
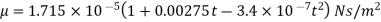
Viscosity of Liquids
Liquid | Viscosity at various temperatures  | |||||
 |  |  | 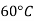 | 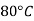 |  | |
Water | 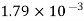 |  |  | 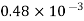 | 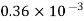 | 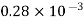 |
Alcohol | 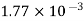 | 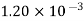 | 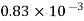 |  |
|
|
Kerosene | 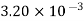 | 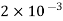 | 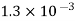 | 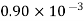 |
|
|
Petrol |  | 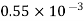 | 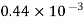 | 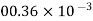 |
|
|
Viscosity of Air at various Temperature
Temperature | 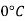 | 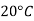 |  | 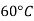 |  |  |
Viscosity 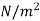 |  | 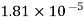 | 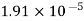 | 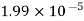 | 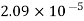 | 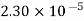 |
Key takeaways
The viscosity of the fluid is due to two contributing factors, namely the interaction between fluid molecules and the transfer of pressure between molecules. In the case of gases the penetration between molecules is large and therefore the interaction of molecules is small.
Newton's viscosity law states that the shear pressure between adjacent water layers is equal to the velocity gradients between these two layers.
The shear pressure ratio and shear ratio are constant, at a given temperature and pressure, and are defined as viscosity or coefficient of viscosity.
Newton’s Law of viscosity, 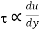
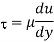
Where,
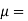 Viscosity
Viscosity
 Shear stress=F/A
Shear stress=F/A
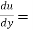 Rate of shear deformation
Rate of shear deformation
Examples:
Q.1 A skater weighing 1000 N attains a speed of 72 km/hour on ice, average skating area being 10 cm². The dynamic coefficient of friction between the Skater and ice may be taken as 0.015. Determine the average thickness of water. layer existing between the skater and the skating surface. Viscosity of water at 0°C may be taken 1 x 10 N-s/m².
Soln.:
Given:
W=1000N,
u = 72 kmph = 72x=20m/sec,
A = 10 cm² = 10 x 10 m², -0.015, 10¹N-s/m²
To find: Average thickness.
Force responsible for motion = Frictional resistance
F = μN=pW
Where N= W
F= 0.015 x 1000 = 15 N
Newton's law of viscosity

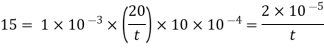
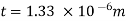
Average thickness of water layer is 1.33 x 10 m
Q.2 A body weighing 1000 N slides down at a uniform speed of 1 m/s along a lubricated Inclined plane making 30° angle with the horizontal. The viscosity of lubricant is 0.1 kg/ms and contact area of the body is 0.25 m². Determine the lubricant thickness assuming linear velocity distribution. -June 2011. 6 Marks
Soln.:
Given:
W= 1000 N,
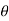 = 30°
= 30°
du = V = 1m/s,
A=0.25 m²
H=0.1 kgm/s 0.1x9.81 Nm/s = 0.981 Nm/s
To find: Lubricant thickness t
Shear force= Weight component along plane
= 1000 sin 30
F = 500 N
Shear stress
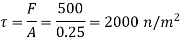
By Newton's law of viscosity
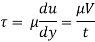
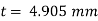
The lubricant thickness is 4.905 mm.
Key takeaways
Newton's viscosity law states that the shear pressure between adjacent water layers is equal to the velocity gradients between these two layers.

Fig no 2 Vapour pressure
Measurement and uses
Key takeaways
Vapor pressure (or vapor pressure in British English; see spelling difference) or equilibrium moisture pressure is defined as the pressure exerted by the smoke on the thermodynamic equilibrium and its thick (solid or liquid) phases at a given temperature in a closed system.
Equilibrium pressure is an indicator of evaporation rate. It is related to the tendency of particles to leak into a liquid (or solid). An object with a high vapor pressure at normal temperatures is often called an invariant.
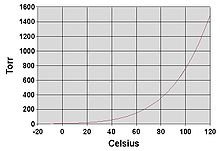
Fig no 3 Boiling point
Log 10 (P/ 1 Torr) = 8.07131 -[( 1730.63 °c) / (233.426° c + Tb)]
Tb = [1730.63 °c/ (8.07131 - log 10(P/ 1 Torr))] - 233
Where the temperature Tb is the boiling point in degree Celsius and the pressure P is in Torr
Relation between the normal boiling point and the vapour pressure of liquid
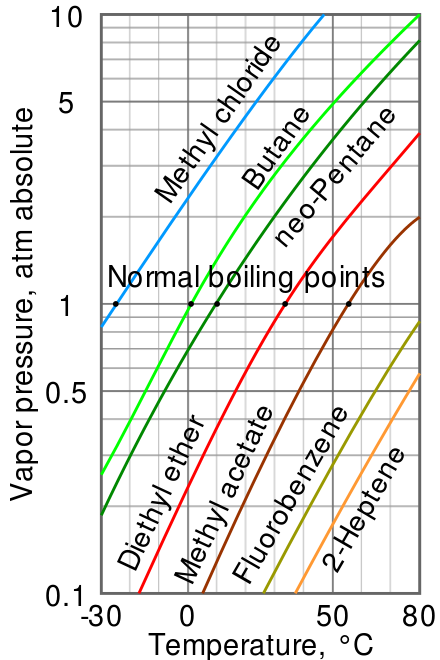
Fig no 4 Log linear Vapour pressure chart
Key takeaways
The boiling point of a liquid varies depending upon the surrounding environmental pressure. A liquid in a partial vacuum has a lower boiling point than when that liquid is at atmospheric pressure.
A liquid at high pressure has a higher boiling point than when that liquid is at atmospheric pressure. For example, water boils at 100 °C (212 °F) at sea level, but at 93.4 °C (200.1 °F) at 1,905 meters (6,250 ft) altitude. For a given pressure, different liquids will boil at different temperatures.
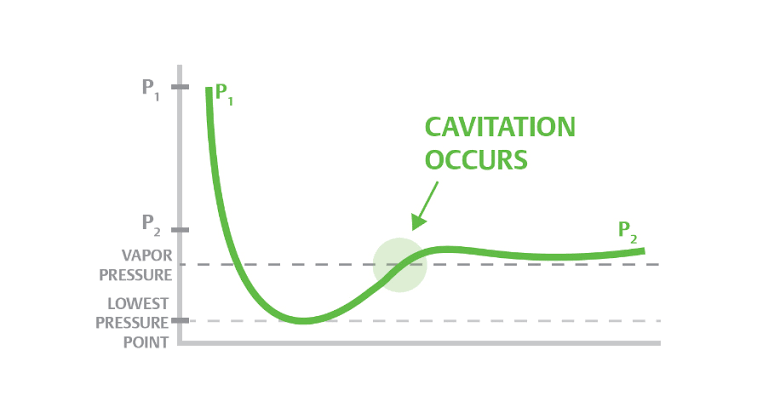
Fig no 5 Cavitation
Avoiding Cavitation
Cavitation can be generally avoided
This can be done by:
Redesign Components Launch High Speed and Low Static Pressure
Walking and injury can be avoided by using special equipment designed for extreme conditions.
Increasing total or local pressure in the system
Key takeaways
Cavitation is a process in which a decrease in pressure to or under pressure from a liquid vapor leads to the formation of vapor-filled pores in the liquid. When placed under high pressure, these gaps, called "bubbles" or "voids", collapse and can create shocking waves that can damage equipment. These shock waves are strong when they are very close to the inserted bubble, but they quickly become weak as they spread away from the insert
Causes
Effect of surface tension
Water
Many of the effects of global conflict can be seen in ordinary water:

Fig no 6 Water bending on leaf

Fig no 7 Water dripping from a tap

Fig no 8 Water striders stay atop the liquid because of surface tension

Fig no 9 Lava lamp

Fig no 10 Tears of wine
Surfactants
Surface tension is seen in other common causes, especially when surfactants are used to reduce it:
Examples:
Q.1 Calculate the gauge pressure and the absolute pressure within:
(1) a droplet of water 0.3 cm in diameter
(2) a jet of water 0.3 cm in diameter.
Assume the surface tension of water as 0.07 N/m and atmospheric pressure as 101.3 N/m² Dec. 2010, 4 Marks
Soln.:
Given:
d = 3mm = 3 x 10³ m.
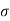 water = 0.073N/m.
water = 0.073N/m.
Patm = 101.3 N/m² atm
For droplet and air bubble
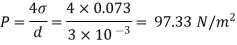
Absolute pressure. (P) = Pgauge + Patm = 97.33 + 101.3 = 198.63 N/m²
For jet

Absolute pressure in jet
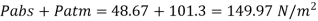
Q.2 Determine the diameter of a droplet of water in mm it t pressure inside is to be greater than that outside by 13 Nm². Take a 7.26 10 Nm.
Soln.:
Given:
P-130 N/m²
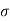 = 7.26×10^-2 N/m
= 7.26×10^-2 N/m
For droplet, P
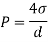

The diameter of a droplet of water is 2.33 mm
Q.3 In the surface tension at air water interface is 0.070 Nm what is the pressure difference between inside and outside of an air bubble of diameter of 0.01 mm?
Soln.:
Given: -
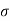 = 0.07 Nm.
= 0.07 Nm.
D= 001mm= 0.01 = 10 m
An air bubble has only one surface,
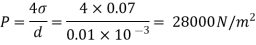
The pressure difference between inside and outside of an air bubble is P= 25000N/m2
Q.4 Calculate the pressure inside a soap bubble of 50mm diameter. Take surface tension at the soap air interface as 0.1Nm
Soln.:
Given:
 = 0.1Nm,
= 0.1Nm,
d=50x10^-3 mm
For soup bubble, P
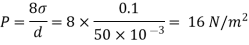
The pressure inside a soup babble is 16 N/m2
Q. 5 If the surface tension at air water interface is 0.075 N/m, what is the pressure difference between inside and outside of an air bubble of diameter of 0.01 mm?
Soln.:
Given:
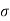 water = 0.075N/m,
water = 0.075N/m,
d=0.01mm
An air bubble has only one surface,
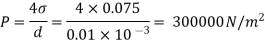
The pressure difference between inside and outside of an air bubble is P=30000N/m2
Q. 6 What force is necessary to it a thin platinum wire ring of negligible thickness having 5 cm diameter from a water surface? Neglect weight of wire and consider surface tension of water as 0.0725 Nm.
Soln.:
Given: -
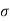 = 0.0725 N/m,
= 0.0725 N/m,
D= 5 cm = 0.05m
Force required to lift a than wire ring

Key takeaways
Surface tension is the tendency for the liquid to shrink into the smallest possible area. Facial friction allows insects (e.g. water arrows), to float and slide on the surface of water without immersion.
Where fluids combine with air, the resulting incompatibility arises from the greater attraction of liquid molecules to each other (due to bonding) than to air molecules (due to adhesion).
There are two main processes in play. One is the internal energy of the extra molecules that make the liquid enter. The second is the gravitational force associated with the surface of the membrane. The effect of the net is that the liquid behaves as if its surface was covered with a thick membrane.
Key takeaways
Capillary action (sometimes capillarity, capillary motion, capillary effect, or wicking) is the ability of fluid to flow in small areas without assistance, or even to counteract external forces such as gravity.
The effect can be seen in the formation of fluid between the hairs of the paint brush, in a thin tube, in the smooth material such as paper and cement, in other non-abrasive materials such as sand and carbon fiber, or organic cell.
Examples:
Q.1 A 10 mm glass tube is inserted into trough containing mercury. Find the capillary effect when the contact angle is: () 180 and (0) 110 Take surface tension of mercury in contact with air as 0.51 N/m. Dec. 2014.3 Marks
Soln.:
Given: d = 10 mm= 10 x 10 m,

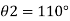
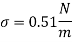
For mercury p=13600 kg/m²
To find: Capillary effect
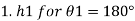
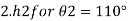
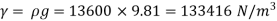
1) Case 1: 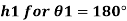
Weight density for mercury


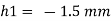
Negative sign indicates capillary depression.
2) Case 2: 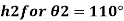
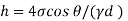
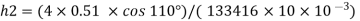
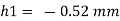
Negative sign indicates capillary depression
Q. 2 Two wide clean glass plates are held parallel with a gap of 1mm between them. What will be the rise of water level between these plates when dipped in water? Assume surface tension for water as 0.0730 N/m.
Soln.:
Given:
t=gap=1 mm
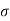 =0.073 N/m
=0.073 N/m
For two wide clean glass plates, 

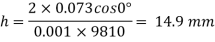
Capillary rise is 14.9 mm.
Q.3 A clean tube of internal diameter 3 mm is immerged in a liquid with a coefficient of surface tension 0.48 N/m. Angle of contact of the liquid with the glass can be assumed to be 130%. The density of the liquid is 13600 kg/m". What would be the level of the liquid in the tube relative to the free surface of the liquid outside the tube?
Soln.:
Given:
d= 3 mm,
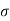 = 0.48 N/m
= 0.48 N/m
The capillary rise (or depression) is given as
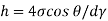
For mercury = 130°. 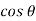 =-0.6428
=-0.6428
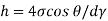

h= - 3. 083 mm
The negative sign indicates that there is capillary depression.
Q. 4 Find the height through which water rises by capillarity action in a glass tube of 2 mm bore, if the surface tension at the prevailing temperature is 0.0736 N/m. Assume angle of contact of glass with water -0°
Soln.:
Diameter of glass tube d=2 mm=2x10-3 m
Surface tension=0.0736 N/m
Angle of Contact 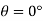
Capillary rise
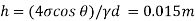
h= 15 mm
The height by which water rises by capillary is 15 mm.
Q. 5 A glass tube of internal diameter 0.2 mm is immersed in mercury. The angle of contact of mercury with glass can be taken as 130 W lat will be the level of Hg in the tube relative to the free surface of the liquid outside the tube? Take surface tension of liquid = 0.5 N/m Dec. 2010, 6 Marks
Soln.:
Given: d= 0.2mm,
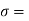 0.5 N/m
0.5 N/m
The capillary rise (or depression) is given as
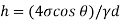
For mercury
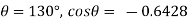


The negative sign indicates that there is capillary depression.
Q. 6 Determine the minimum size of glass tube that can be used to measure water level, if the capillary rise in the tube is not to exceed 0.25 mm, Take surface tension of water in contact with air As 0.0735 N/m. May 2013, 6 Marks
Soln.:
Given:
h=0.25 mm,
 =0.0735 N/m,
=0.0735 N/m,
To find: Minimum size of glass tube 'd'.
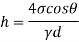
for water 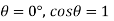
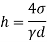
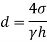
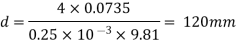
Q.7 State the minimum diameter of glass tube to be immersed in water, for which capillarity effects are to be limited up to 2.08mm Take surface tension of water in contact with air as 0.073 N/m. June 2011; 2 Marks
Soln.:
Given:
h=298mm,
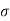 =0.073 N/m,
=0.073 N/m,
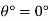 for glass plates
for glass plates
To find: Diameter of tube,
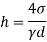
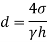
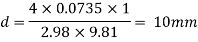
The diameter of glass tube immersed in water is 10 mm.
Delta = stress / strain
where the pressure is the force that causes the change to be divided by the area in which the force and gravity are used is the rate of change of a particular parameter caused by the distortion in the actual parameter value. Since the difficulty is flawless, the delta will be the same as the units of pressure.
Determining how pressure and complexity will be measured, including indicators, allows for many types of expandable model to be defined. The three main ones are:
Examples:
Q.1 Determine the Bulk modulus of elasticity of a liquid, which is compressed in a cylinder from a volume of 0.0125 m³ at 80 N/cm² pressure to a volume of 0.0124 m³ at 150 N/cm² pressure?
Soln.:
Given:
Initial volume V = 0.0125 m²,
Final volume = 0.0124 m³
dV = Decreases in volume = 0.0125 -0.0124 = 0.0001m³
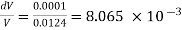
Initial pressure = 80 N/cm2
Final pressure - 150 N/cm
Increases in pressure = 150-80= 70 N/cm = 70 x 10^4 N/m²
Bulk modulus K
 Change in pressure/(change volume/ original volume)
Change in pressure/(change volume/ original volume)
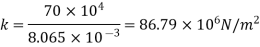
The Bulk modulus of elasticity of a liquid is 56.79 x 10^6 N/m2
Q.2 Determine the Bulk modulus of elasticity of a liquid, if the pressure of the liquid is increased from 400 Pa to 1200 Pa. The volume of the liquid decreases by 0.15% June 2010, 4 Marks
Soln.:
Given:
Initial pressure 400 Pa,
Final pressure 1200 Pa,
dV = 0.15% V
Increases in pressure
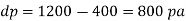
Decreases in volume
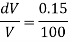
Bulk modulus
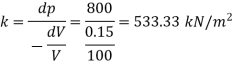
Q. 3 A cylinder contains a liquid of volume of 0.02 m' at pressure of 700 Pa when compressed to reach a volume of 0.019 m The pressure is increased to 1400 Pa. Find bulk modulus of elasticity Dec. 2011, 2 Marks
Soln.:
Given:
Initial volume 0.02 m²
Final volume 0.019 m
Change in volume dv=0.02- 0.019 = 1x 10^-3 m^3
Change in pressure dp = 1400-700 = 700 Pa
Bulk modulus k

Q.4 If the bulk modulus of elasticity of water is 2.07 x 10° kN/m²:
(1) What is the pressure required to reduce its volume by 2%?
(ii) What will be the change in mass density?
Soln.:
Given:
K=207 x 10 kN/m²
dV/V= 2%
 for water = 1000 kg/m
for water = 1000 kg/m
To find: dp, d
1) Pressure required to reduced its volume by 2%



2) Change in mass density
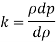
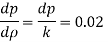
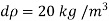
Key takeaways
An elastic modulus (also known as a modulus of elasticity) is a value that measures an object or object to the object of a highly deformed object (i.e., non-permanent) in which pressure is applied. The expandable modulus of the material is defined as the slope of the pressure point in the region of the elastic deformation: Solid material will have a very high modulus. The elastic modulus has the following form:
Delta = stress / strain
Examples:
Q.1 A pressure of 1.2 M Pascal is applied to 350 liters of liquid, causes a volume reduction of 1.5 liters. Calculate bulk modulus of elasticity for the liquid also find the compressibility.
Soln.:
Given:
Pressure p= 1.2M,
Pascal = 12x10 N/m².
Volume V 650 liter= 650 x 10³ m.
Reduction in volume dV= 1.5 liter= 1.5 x 10^-3 m3
Bulk modulus of elasticity, K
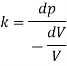
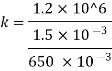
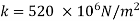
Compressibility
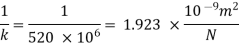
The Bulk modulus of elasticity for the liquid is 520 M Pa and compressibility is 1.923 x 10 m/N.
Q. 2 At a depth of 5 kilo meters in the ocean the pressure 480 kg/cm Assuming specific weight at the surface as is 1025 kgm and that the average modulus of elasticity is 24 x 10 kg/cm for that pressure range. Calculate:
a) The change in specific volume between the surface and the given depth
b) Specific volume at the given depth and
c) Specific weight at that depth.
Soln.:
Given:
Pressure dp = 480 kg/cm²
Average modulus of elasticity K = 24 x 10' kg/cm
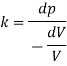
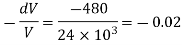
Specific volume of the water at the surface of the ocean,
Specific volume
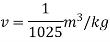
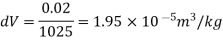
Specific volume at the depth of 5 km,
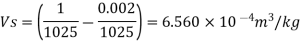
Specific weight of water at the depth of 5 km,
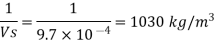
Q.3 At a depth of 2 km in an ocean, the pressure is 840 bar. Assume the specific weight at surface as 10,250 N per m² and the average Bulk modulus of elasticity as 2.4 x 10° kN per sq.m. for that pressure range.
1) What will be the change in specific volumes between that at the surface and at that depth?
2) What will be the specific volume at that depth?
3) What will be the specific weight at that depth?
Soln.:
Given:
P₁ = 840 x 10¹ Pa,
H1, = 2 km = 2000 m.
 = 10250 N/m²,
= 10250 N/m²,
K = 2.4 x 10' Pa
Bulk modulus K
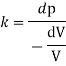
And 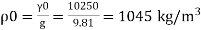
Specific volume
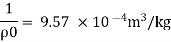
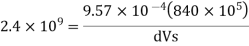
Change in specific volume
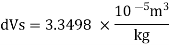
Specific volume at 2 km depth
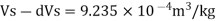
Density at 2 km depth
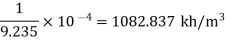
Specific weight
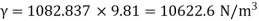
Key takeaways
Compression is an asset to be reduced to a minimum by pressure. This material is the result of porosity, and the change in mass occurs from particles that come close together by pressure.
References:
1. Tech max
2. Fluid mechanics and machinery R Berndtsson and P.N. Chadramouli
3. Hydraulic and fluid mechanics, PM Modi and SM Seth
4. Theory and applications of fluid mechanics, K Subramanya, Tata McGraw Hill
5. Fluid mechanics with engineering applications, RL Daughterty, JB Franzini