Unit - 3

Bending moment and shear force diagrams

3.1 Bending moment (BM) and Shear force (SF) diagrams

1. Bending moment’s diagrams

The bending moment at any cross section of the beam is defined as the algebraic sum of moment of all the forces either left or right of the section.

BM= (∑MF) L = (∑MF) R

Bending moment is the response brought about in a structural detail whilst an outside pressure or second is carried out to the detail, inflicting the detail to bend

The inner response hundreds in a cross-segment of the structural detail may be resolved into a resultant pressure and a resultant couple. For equilibrium, the instant created via way of means of outside forces (and outside moments) should be balanced via way of means of the couple brought about via way of means of the inner hundred. The resultant inner couple is known as the bending moment at the same time as the resultant inner pressure is known as the shear pressure.

The bending moment at a segment C because of a unit load at X can further be received via way of means of direct equilibrium. The form of bending second diagram can be triangular with the peal cost going on under the unit load location. For this reason, the bending second at any segment because of a un it load is most whilst the burden acts precisely on the segment below consideration.

If clockwise bending moments are taken as terrible (negative), then a terrible bending moment inside a detail will cause "hogging", and a superb (positive) second will cause "sagging". It is consequently clean that a factor of 0 bending moment inside a beam is a factor of contra flexure—that is, the factor of transition from hogging to sagging or vice versa.

Sign convention of bending moment

Sagging bending moment: when clockwise moment on the left of the section or anticlockwise moment on the right of the section is considered as positive B.M. Or sagging B.M.

Hogging bending moment: when the anticlockwise moment on the left of the section or clockwise moment on the right of the section is considered as negative or hogging B.M.

The bending moment obtained analytically are represent by plotting bending moment as ordinate (y- axis) against the position of cross section as abscissa (x- axis) the diagram obtained is called bending moment diagram.

The bending moments are sagging throughout the beam and hence according to our usual sign convention they have positive value.

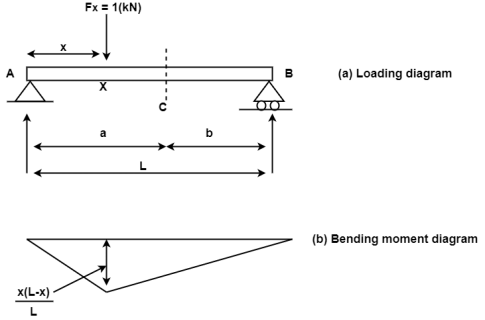
Fig:1

2. Shear Force diagrams:

The shear force at the cross section of a beam is defined as the algebraic sum of all the unbalanced vertical forces either left or right of the section.

SF = (∑ Fy) L = (∑ Fy) R

This is special to compression, which takes place while the two opposing forces are pushing into every different on the identical point (i.e., they may be not offset), ensuing in compressive stress.

When a structural member experiences failure through shear, components of it are driven in special directions, for example, while a piece of paper is reduced through scissors.

A shear force is a force implemented perpendicular to a surface, in competition to an offset force appearing within side the contrary direction

Sign convention for shear force:

An upward force to the left of section or downward force to the right of a section will be considered as a positive shear force.

When the force is downward to the left side of section and upward on the right of a section, will be considered as a negative shear force.

The shear force obtained analytically are representing by plotting shear force as ordinate (y- axis) against the position of cross section as abscissa (x- axis) the diagram obtained is called as shear force diagram.

Fig:2

3.2 BM and SF diagrams for cantilevers simply supported and fixed beams with or without overhang.

1. BM diagram and SF diagram for simply supported beam:

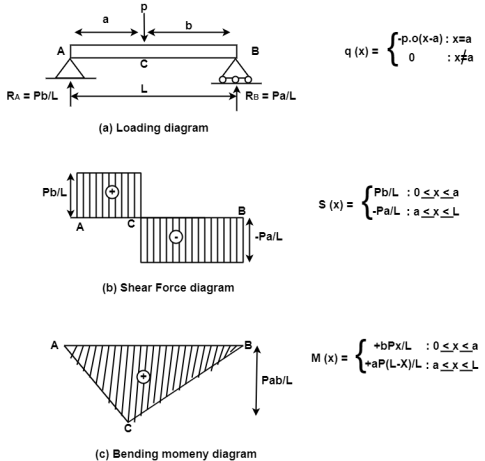
Fig: 3

2. SF diagram and BM diagram for cantilever beam:

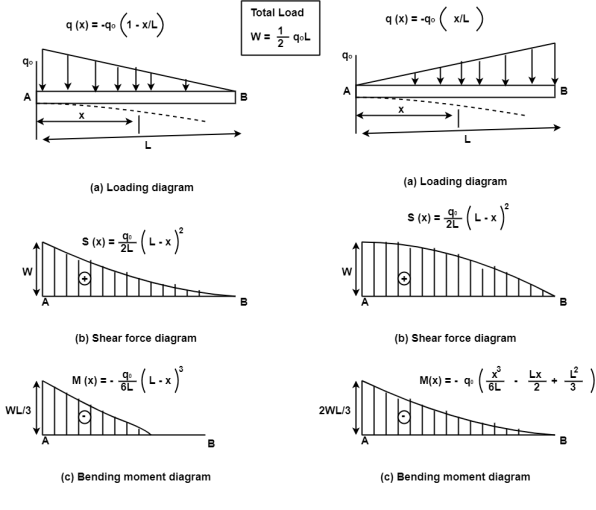
Fig:4

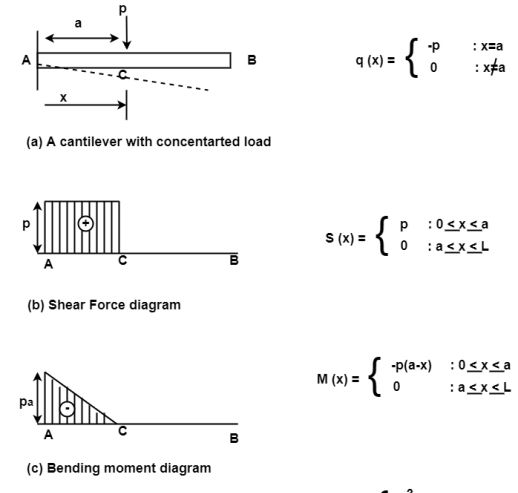
Fig:5

3.3 Calculation for maximum BM and SF and point of contra flexure under concentrated loads

1. Calculation of maximum BM and SF:

A. Maximum Bending moment:

Consider a section x-x at the distance x- from left support

∑ (BM)XX = WL/2. X- (W.X) X/2 = WL/2 = WX2/2

Bending moment equation shows that BM curve is parabolic

At x=0    BMA = 0

At X= L      BMB = WL/2 X L – WL2/2 = 0

Position and magnitude of maximum BM

Maximum bending moment occurs where shear force is zero.

Now location of point where SF = 0

∑ (SF) XX = 0

WL/2 – WX = 0

Therefore x= L/2

Bending moment at x = L/2

BM = WL/2 (L/2) – W/2 (L/2)2 = WL/4-WL2/8

BM = WL2

           8   

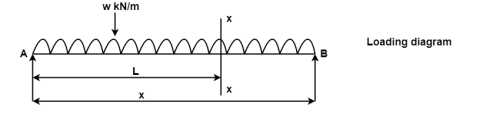
Fig:6

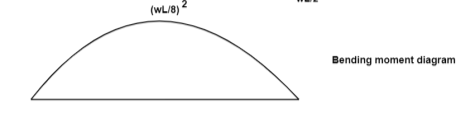
Fig:7

B.  Maximum Shear force calculation:

Consider a section x-x at the distance X from A

∑ (SF)XX = WL/2 –WX

At x = 0, SFA = WL/2

At x= L, SFB = WL/2- WL = -WL/2

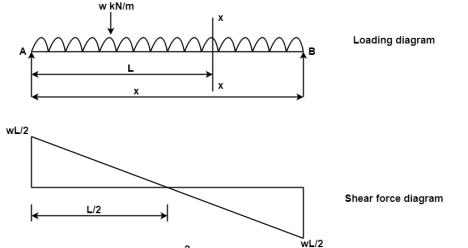
Fig:8

2. Point of contra flexure under concentrated load:

It is the point at which bending moment diagram change its sign generally bending moment at the point is equal to zero. It is definitely occurring in case of overhang beam within support. Point of contra flexure is calculated by equating expression of B.M.

BMXX = 0

Fig:9

3.4 Uniformly distributed loads over the whole span or part of span

1. Uniformly distributed load over the whole span:

Analysis for fixed beam carrying a UDL throughout the span

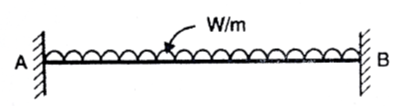
Fig:10

Solution:

A fixed beam AB carrying udl of W/m over the entire span

1. Fixed beam as a simply supported bam draw free BMD

Free BMD corresponding beam AB as simply supported

Fig:11

2.     Draw fixed BMD

A loading is symmetrical then MA= MB

Fig:12

3.     Find A and x of free BMD and fixed BMD

Area of free BMI (A) = 2/3 Lh

X= L/2 = 2/3 L. (WL2/8)

AF = MA x L = MB x L = M x L = WL3/12

XF = L/2

4.     Find fixed end moments

Due to symmetry MA = MB

A = AF

WL3/12 = MAL

MA = WL2/12      (Hogging)

MB = WL2/12      (Hogging)

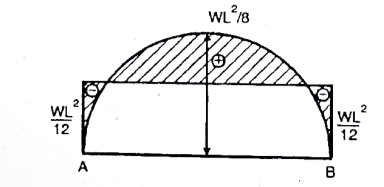
Fig:13

5.     Final BMD and shear force calculation (Final SFD)

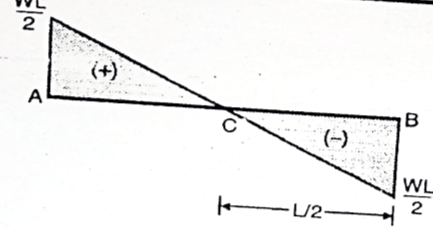
Fig:14

2. Uniformly distributed load part of span

Analysis of fixed beam carrying a UDL on some portion (span)

Solution:

A fixed beam AB carrying uniformly distributed load of w/m

Consider an element section

For whole span integrated

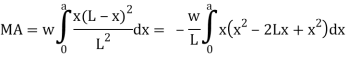
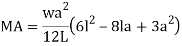
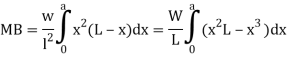
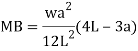
Example:

A simply supported beam of span L is carrying uniformly distributed load w over its entire span calculate S.F. And B.M. Also draw SFD and BMD.

Solution:

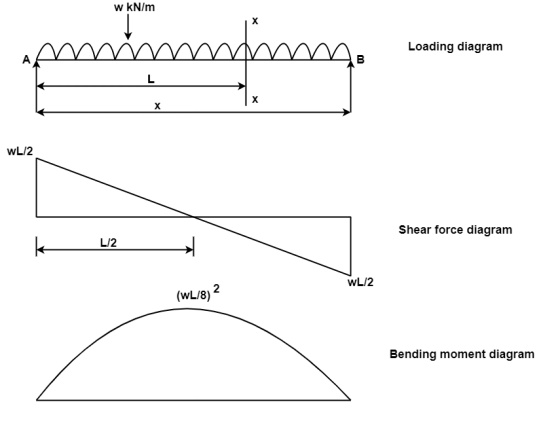
Fig:15

1. Support reaction:

Since the beam is subjected to the symmetrical loading support reactions is half of the total load

RA = RB = W x L

2. Shear force calculation:

Consider a section x-x at the distance X from A

∑ (SF)XX = WL/2 –WX

At x = 0, SFA = WL/2

At x= L, SFB = WL/2- WL = -WL/2

3. Bending moment:

Consider a section x-x at the distance x- from left support

∑ (BM)XX = WL/2. X- (W.X) X/2 = WL/2 = WX2/2

Bending moment equation shows that BM curve is parabolic

At x=0    BMA = 0

At X= L      BMB = WL/2 X L – WL2/2 = 0

Position and magnitude of maximum BM

Maximum bending moment occurs where shear force is zero.

Now location of point where SF = 0

∑ (SF) XX = 0

WL/2 – WX = 0

Therefore x= L/2

Bending moment at x = L/2

BM = WL/2 (L/2) – W/2 (L/2)2 = WL/4-WL2/8

BM = WL2

           8    

Key takeaway:

1. Find support reaction

2. Find shear force

3. Find bending moment

4. Draw SFD

5. Draw BMD.

3.5 Combination of concentrated loads (two or three)

Concentrated load

This form of load acts exceedingly on a smaller area. For example, the pressure exerted via way of means of a chair or a desk leg at the helping ground or load exerted via way of means of a beam on a helping column are each taken into consideration to be focused load.  In the derivation of the primary differential equation of equilibrium the loading depth turned into comfortably modeled as a non-stop variable.

Fig:16

3.6 Uniformly Distributed Loads

In a simply supported beam subjected to uniformly distributed load. The load intensity is a constant where by the shear force diagram will have a linear variation. Also note that the value of the shear force at the extremities will be equal to vertical reaction at A and B. The bending moment diagram will have a quadratic variation owing to the linear variation of the shear force diagram. It has maximum value at the mid span location where the shear force changes its sign the slope of the beam will have a cubic variation and hence the deflection will have a fourth order variation. Its magnitude is designated by its intensity (N/m or KN/m).

Fig:17

3.7 Uniformly Varying Loads

This type of load will be uniformly varying from zero intensity at one end to the designated intensity at the other end. A triangular block of brickwork practically imposes such a loading on a beam

The behavior of beam depends on which end (free end or fixed end) the load intensity is maximum. When load intensity is maximum at the free end the bending moment and deflection throughout the beam are bound to be larger compared to the case where the load intensity is maximum at the fixed end. The support reaction at A will be same in both the beams and shear force in the beam at a will also be identical for both. A shear force (SF) is defined as the algebraic sum of all the vertical forces, either to the left or to the right-hand side of the section.

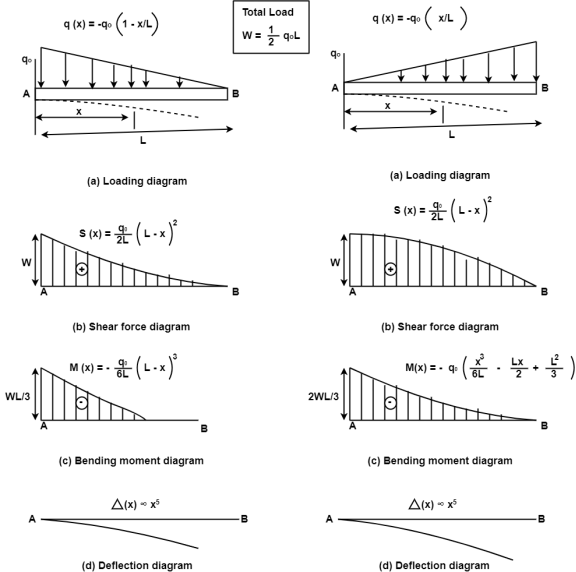
Fig:3.18

Example:

A simply supported beam of length 6 m carries point load of 3 KN and 6 KN at distances of 2 m and 4 m from the left end. Draw the shear force and bending moment diagrams for the beam

Fig:19

Solution:

Find reaction RA and RB.

Upward load =Downward loads

RA+ RB = 9 KN

Taking moments of the force about A,

RBx6 = 3x2 + 6x4

30RB =5kN

RA= 4kN

Mechanics of Materials

18 M EI 33

Taking moments of the force about A,

RBx6 = 3x2 + 6x4

30RB=5kN

RA= 4kN

Shear Force

FA= + RA= + 4kN

Shear force between A and C is constant and equal to + 4 KN

Shear force at C,

Fc = + 4 -3.0 = + 1kN

Shear force between C and D is constant and equal to + 1 KN.

Shear force at D,

FD= + l -6 = -5kN

The shear force between D and B is constant and equal to -5 KN

Shear force at B,

FB= -5KN

The shear force diagram is drawn as shown in Fig.

Fig:20

Bending Moment Diagram

B.M.at A,

MA=0

B.M.at C,

Mc= RA x 2 = 4x2 = + 8KN/M

B.M.at D

MD= RA x 4 –3 x 2 = 4 x 4 –3 x 2 = + 10KN/M

B.M.at B,

MB=0

The bending moment diagram is drawn as shown in Fig.

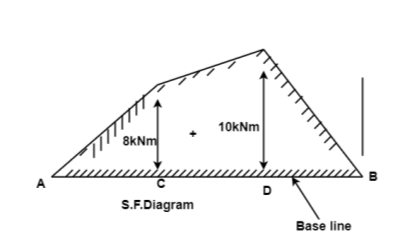
Fig:21

3.8 Applications of Moments

If a frame is in rotational equilibrium, then the sum of the anticlockwise moments is identical to the sum of the clockwise moments.

If a frame is in rotational equilibrium, then the algebraic sum of the moments approximately any factor is zero.

To locate the mass of an object

The bending moment obtained analytically are represent by plotting bending moment as ordinate (y- axis) against the position of cross section as abscissa (x- axis) the diagram obtained is called bending moment diagram.

The bending moments are sagging throughout the beam and hence according to our usual sign convention they have positive value.

Key takeaway:

1. If a frame is in rotational equilibrium, then the sum of the anticlockwise moments is identical to the sum of the clockwise moments.
2. If a frame is in rotational equilibrium, then the algebraic sum of the moments approximately any factor is zero.
3. To locate the mass of an object

Numericals

Q. Draw shear force and bending moment diagram for beam loaded as shown in figure.

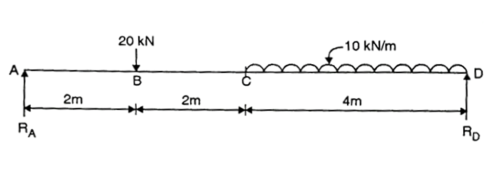
Fig:22

Step 1: Support Reaction

=0

202+(10×4) × (+4)-RD×8=0

RD=280/8

RD=35KN

=0

RA+RD-20-10×4=0

RA=60-35

RA=25KN

Step 2: Shear force calculation:

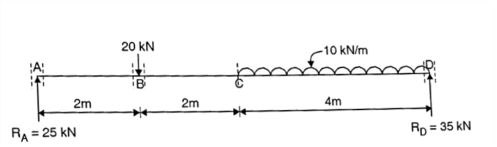
Fig:23

Fig:24

SFAL=0

SFAR=25KN

SFBL=25KN

SFBR=25-20=5KN

SFC=5KN

SFDL=5-10×4

=-35KN

SFDR=-35+35

=0

Step 3: Bending Moment Calculation:

Fig:25

BMA=0

BMB=25×2=50KN.m

BMc=25×4-20×2

=60KN.m

BMD=25×8-20×6-10×4×4/2

=0

Step 4: Position of zero shear force

Consider section x-x at a distance x from A between CD.

=25-20-10(x-4) =0

5=10(x-4)

0.5=x-4

X=4.5 m from A

Step 5: Maximum Bending Moment

Mmax=25×20(x-2)-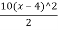

=25×4.5-20(4.5-2)-

=61.25KN.m

Step 6: SFD and BMD

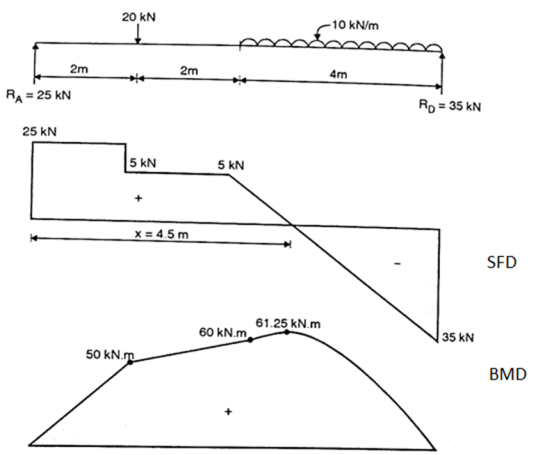
Fig:26

Q. Draw the S.F and B.M diagrams indicating principal value for an overhanging beam ABC with AB=6m and BC=3m.It is loaded with u.d.l of intensity 2KN/m all over the span in addition to a point load 5KN at free end ‘C’. Also locate the point of contraflexure.

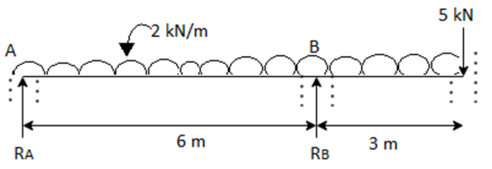
Fig:27

Step 1: Support Reaction:

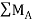=0

-RB×6+2×92/2+5×9=0

∴RB=21KN

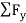=0

RA+RB-(2×9)-5=0

RA=2KN

Step 2: Shear force calculation:

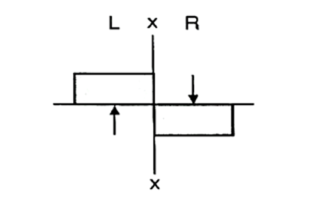
Fig:28

SFAL=0

SFAR=2

SFBL=2-2×6=-10KN

SFBR=-10+21=11KN

SFCL=11-2×3=5KN

SFCR=5-5=0

Step 3: Bending Moment calculation:

Fig:29

BMA=0

BMB=2×6-2×62/2=-24KN.m

BMC=0

Step 4: Position of maximum bending moment Max.BM occurs where S.F is zero.

SFxx=0

2-2x=0

∴x=1m

BMmax=2x-2x2/2=2×1-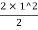=2-1=1KN.m

Fig:30

Point of contraflexure:

BMxx=0; 2x-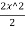=0

2=x:1

X= 2m from support A

Q. Plot the shear force and bending moment diagram for the beam loaded as shown in fig.

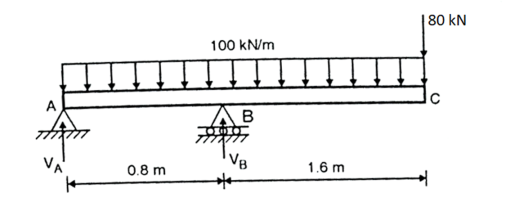
Fig:31

Step 1: Support Reaction

=0

-VB×0.8+100×2.42/2+80×2.4=0

VB=480/0.8=600KN

=0

VA+VB-100×2.4-80=0

VA+600-240-80=0

VA=-280KN

Step 2: Shear force calculation

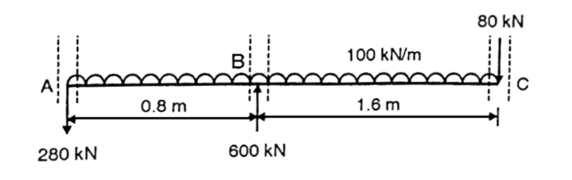
Fig:32

SFAL=0

SFAR=-280KN

SFBL=280-100×0.8=-360KN

SFBR=-360+600=240KN

SFCL=240-100×1.6=80KN

SFCR=80-80=0

Step 3: Bending moment calculation:

BMA=0

BMB=-280×0.8-100×0.82/2=-256KN.m

BMC=0

Maximum bending moment occurs where shear force is zero.

SFxx=-280-100x+600=0

X=320/100=3.2m

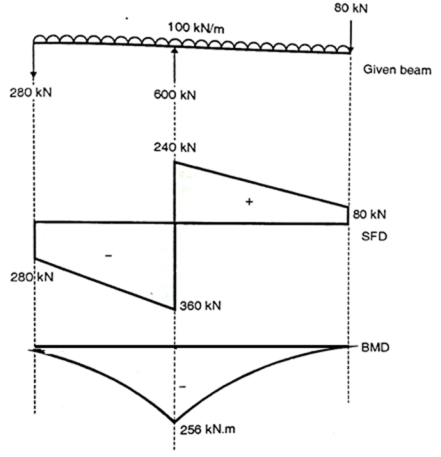
Fig:33

Q. For an overhanging beam showing in the fig. Determine the support reactions at A and B and draw shear force and bending moment diagrams. Determine the point of contraflexure within the span AB.

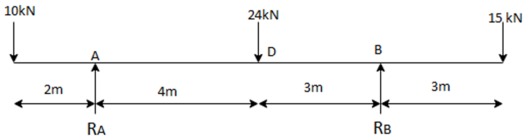
Fig:34

Step1: Support reaction:

=0

∴-10×2+24×4-RB×7+15×10=0

=0

∴RA+RB-10-24-15=0

RA+(32.29)-10-24-15=0

∴RA=16.71KN

Step 2: Shear force Calculation:

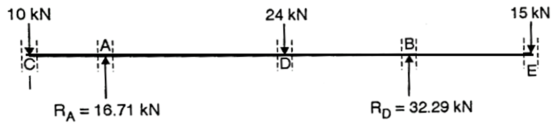
Fig:35

SFCL=0

SFCR=-10KN

SFAL=-10KN

SFAR=-10+16.71=6.71KN

SFDL=6.71KN

SFDR=6.71-24=-17.29KN

SFBL=-17.29KN

SFBR=-17.29+32.29=15KN

SFEL=15KN

SFER=15-15=0

Step 3: Bending moment calculation:

Fig:36

BMC=0

BMA=-10×2=-20KN.m

BMD=-10×6+16.71×4

=6.84KN

BME=0

BMB=-10×9+16.71×7-24×3

=-45KN

Step 4: SFD and BMD

Fig:37

Step 5: Point of contraflexure:

Consider BMD between AB and by similarity of triangles,

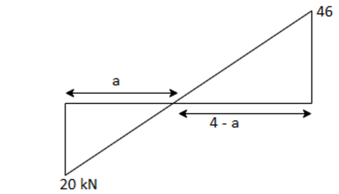
Fig:38

=

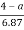
a =2.8m

∴x1=a+2=2.8+2=4.8m

Consider BMD between DB and by similarity of triangles.

Fig:39

=

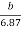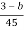
∴b=0.397m=0.4m

∴x2=b+6=0.4+6=6.4m

Q. Draw Shear force and bending moment diagrams for the beam loaded as shown in fig.

Fig:40

Step 1: Support Reaction

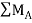=0

100×2+60+50-RB×10=0

RB=31KN

=0

∴RA+RB-100=0

RA=69KN

Step 2: Shear force calculation

Fig:41

SFAL=0

SFAR=69KN

SFCL=69KN

SFCR=69-100=-31KN

SFBL=-31KN

SFBR=-31+31=0

Step 3: Bending moment calculation

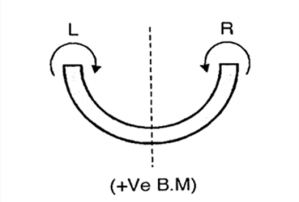
Fig:42

BMA=0

BMC=69×2=138KN.m

BMDL=69×4-100×2=76KN.m

BMDR=76+60=136KN.m

BMEL=69×7-100×5+60=43KN.m

BMER=43+50=93KN.m

BMB=0

Step 4: SFD and BMD

Fig:43

Q. Draw SFD and BMD for the beam shown in fig. Indicate the numerical values at all important sections. Find the position of contra flexure, magnitude and position of maximum BM.

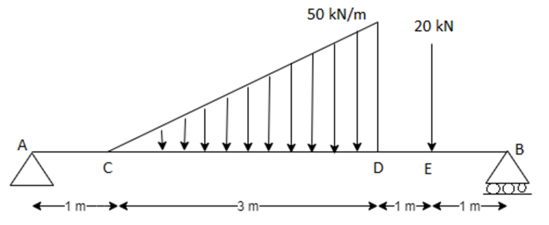
Fig:44

Step 1: Support reaction

=0

-VB×6+20×5+(1/2×3×50) (1+2/3×3)=0

-6VB+100+(75×3)=0

VB=54.17KN

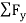=0

VA+VB-(1/2×3×50)-20=0

VA=40.83KN

Step 2: Shear force calculation:

Fig:45

SFAL=0

SFAR=40.83KN

SFC=40.83KN

SFD=40.83-(1/2×3×50)=-34.17KN

SFEL=-34.17KN

SFER=-34.17-20=-54.17KN

SFBL=-54.17KN

SFBR=-54.17+54.17KN

Step 3: Bending Moment Calculation

BMA=0

BMC=40.83×1=40.83KN.m

BMD=40.83×4

=(1/2×3×50)(1/3×3)

=8.32KN.m

BME=54.17×1=54.17KN.m

BMB=0

Maximum B.M occurs where shear force is zero.

∵=

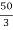
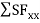=40.83-(1/2×x×16.67x)=0

40.83=8.33x2

X=2.21m

∴Maximum B.M occurs at 1+x =1+2.21=3.31 m from A

BM=40.83×3.31-(1/2×2.21×16.67×2.21)×1/3×2.21=105.1KN.m

Step 4: SFD and BMD

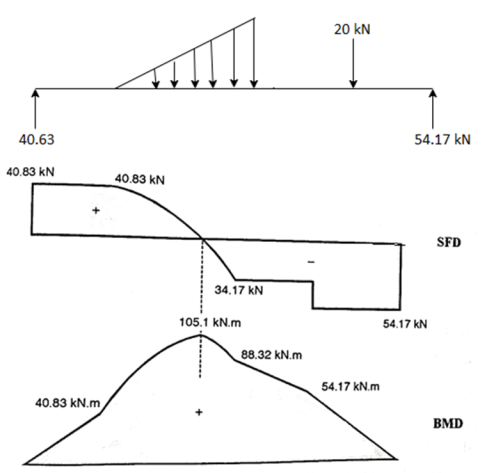
Fig:46

References:

1. Timoshenko, S. And Young, D. H., “Elements of Strength of Materials”, DVNC, New York USA.
2. Kazmi, S. M. A., “Solid Mechanics” TMH, Delhi, India.
3. Hibbeler, R. C. Mechanics of Materials. 6th ed. East Rutherford, NJ: Pearson Prentice Hall, 2004
4. Crandall, S. H., N. C. Dahl, and T. J. Lardner. An Introduction to the Mechanics of Solids 2nd ed. New York, NY: McGraw Hill, 1979
5. Laboratory Manual of Testing Materials - William Kendrick Hall
6. Mechanics of Materials - Ferdinand P. Beer, E. Russel Jhonston Jr., John T. DEwolf – TMH 2002.