Unit - 2
First Law of Thermodynamics
Internal energy may be considered a thermodynamic property. Internal energy is an extensive property because it depends on the mass of the system. Similarly, kinetic and potential energies are extensive properties. Internal energy may at times refer to both internal energy per unit mass and the total energy.
From the lesson Conservation of Energy, raising the temperature of a body increases its internal energy; lowering the body's temperature decreases its internal energy. Therefore, change in internal energy can often be associated with a change in temperature. In the absence of motion, gravity, surface effects, electricity, or other effects, the state of a pure substance is specified by two independent properties. It is very significant that, with these restrictions, the internal energy may be one of the independent properties of a pure substance. This means, for example, that if the pressure and internal energy are specified (with reference to an arbitrary base) of superheated steam, the temperature is also specified. Thus, in a table of thermodynamic properties such as the steam tables, the value of internal energy can be tabulated along with other thermodynamic properties. Most thermodynamic tables should list the internal energy for saturated states. Included should be the internal energy of saturated liquid uf and the internal energy of saturated vapor ufg. The values are given in relation to an arbitrarily assumed reference state, which, for water in the steam tables, is taken as zero for saturated liquid at the triple-point temperature, 0.01°C. All values of internal energy in the steam tables are then calculated relative to this reference (note that the reference state cancels out when finding a difference in u between any two states). Values for internal energy are found in the steam tables in the same manner as for specific volume. In the liquid–vapor saturation region
U = Uliq + Uvap
or:
mu = mliquf + mvapug
Dividing by m and introducing the quality x gives:
u = (1 − x)uf + xug
u = uf + xufg
As an example the specific internal energy of saturated steam having a pressure of 0.6 MPa and a quality of 95% can be calculated as:
u = uf + xufg = 669.9 + 0.95(1897.5) = 2472.5 kJ/kg
In thermostatic, the only energy in a substance is that stored in a system by molecular activity and molecular bonding forces. This is commonly denoted as internal energy. A commonly accepted adjustment to this static situation for fluid flow is to add two more energy terms that arises from Newtonian mechanics.In the study of thermodynamics, it is convenient to consider the bulk kinetic and potential energy separately and then to consider all the other energy of the control mass in a single property that we call the internal energy. The kinetic and potential energy of the control mass are associated with the coordinate frame that is selected and can be specified by the macroscopic parameters of mass, velocity, and elevation. The internal energy U includes all other forms of energy of the control mass and is associated with the thermodynamic state of the system.
Specific heat capacity
Specific heat capacity is the amount of heat energy required to raise the temperature of a substance per unit of mass. The specific heat capacity of a material is a physical property. It is also an example of an extensive property since its value is proportional to the size of the system being examined.
In SI units, specific heat capacity (symbol: c) is the amount of heat in joules required to raise 1 gram of a substance 1 Kelvin. It may also be expressed as J/kg.k Specific heat capacity may be reported in the units of calories per gram degree Celsius, too. Related values are molar heat capacity, expressed in J/mol.K and volumetric heat capacity, given in J/m3•K.Heat capacity is defined as the ratio of the amount of energy transferred to a material and the change in temperature that is produced:
C = Q / ΔT
Where C is heat capacity, Q is energy (usually expressed in joules), and ΔT is the change in temperature (usually in degrees Celsius or in Kelvin).
Enthalpy:
In thermodynamics process constant enthalpy means that enthalpy does not change in all process. Best understand the concept of constant enthalpy we should understand the throttling process.
Throttling Process:
The throttling process is an expansion process in which the pressure reduces after expansion and the velocity is negligible. A throttling expansion occurs when a gas or a vapour is expanded through an aperture of minute dimensions such as a throat or a slightly opened valve.
During the throttling process the expanding fluid is forced through the aperture by its pressure but the hole is so narrow that the frictional resistance between the fluid and the wall reduces the fluid velocity to a negligible amount; as a result, the fluid escapes with a small amount of kinetic energy.
Due to friction kinetic energy reappears as heat and the gas is raised to its initial temperature. During a throttling process no heat is supplied or rejected, no external work is done and in the case of a perfect gas there is no alteration in temperature.
When a fluid expands through a throttle valve or a constricted orifice, the enthalpy before the throttling valve is equal to the enthalpy after throttling. This does not mean, however, that the throttling process is constant enthalpy process. Here the properties before and after the process are defined. Fig.1 shows throttling process.
H1 = H2.
In this process the enthalpy remains constant. The enthalpy at condition 1 is equal to enthalpy at condition 2.
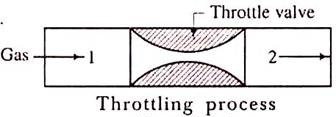
Fig 1
Key points
1) Specific heat capacity is the amount of heat energy required to raise the temperature of a substance per unit of mass.
2) The throttling process is an expansion process in which the pressure reduces after expansion and the velocity is negligible
Energy Balances on Closed Systems
A system is closed if mass does not cross the system boundary during the period of time covered by energy balance. Energy balance for a closed system written between two instants of time is
∆U + ∆Ek + ∆Ep = Q − W
∆U is change internal energy, ∆Ek is change in kinetic energy and ∆Ep is change in potential energy, Q is heat transferred to the system and W is work done by the system. We take heat lost to surroundings as –ve and heat transferred to the system as +ve.
If the system is adiabatic, there is neither gain by the system not heat loss and Q is zero. If there are no moving parts, then W is zero.
Energy Balances on Open Systems
A system is open if mass crosses the system boundary. For such a system, work must be done on the fluid mass to push it into the system and work is done by the fluid mass exiting the system. These two constitute the flow work and should be included in the energy balance. Work could also be done by the fluid mass on moving parts of the system (example: steam driving a turbine). This is called shaft work.
The net rate of work done by an open system on its surroundings includes the works discussed above:
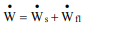
ẇSis the shaft work and ẇn is the flow work.
To understand shaft work, consider a single-inlet and single-outlet system into which fluid enters at Pin (N/m2 ) at a volumetric flow rate of Vin(m3 /s) and leaves the unit at Pout (N/m2 ) at a volumetric flow rate of Vout (m3 /s).
Work required to push the mass in = Pin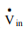
Work done by the fluid exiting the system = Pout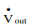 
The net rate of work done by the system = Pin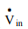
- Pout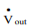
The energy balance takes the following form:
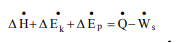
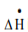is rate of change of enthalpy, a term defined below.
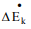is rate of change of kinetic energy and 
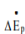is rate of change of potential energy, Q is rate at which energy is transferred to the system and ẇS is the rate at which work is done by the fluid on the system.
We define specific enthalpy (enthalpy per unit mass or mole) as:
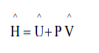
U is specific internal energy, P is pressure and ^ V is specific volume.
Key points
1) Energy balance for a closed system written between two instants of time is
∆U + ∆Ek + ∆Ep = Q − W
2) Specific enthalpy (enthalpy per unit mass or mole) as:
The conservation of mass principle, which has been previously introduced, in rate format, is:
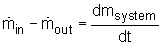
During a steady-flow process, the total amount of mass contained within a control volume does not change with time. That is,
Dmsystem/dt = 0
Hence the conservation of mass principle gives the total amount of mass entering a control volume equal to the total amount of mass leaving it. In an equation format, it is
(Total mass entering the control volume per unit time) = (Total mass leaving the control volume per unit time)
Or,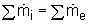 
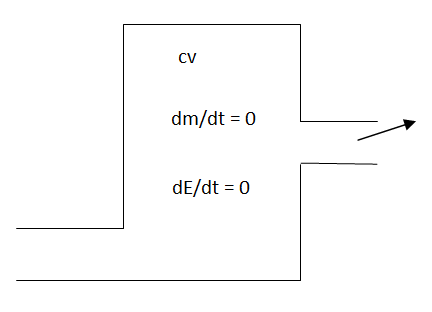
Fig 2
Where
i = inlet
e = exit
Also, the energy balance for a process, which has been previously introduced, in rate format, is:
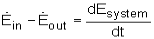
For a steady-flow process, the total energy content of a control volume remains constant. That is,
DEsystem/dt = 0
Thus, the amount of energy entering a control volume in all forms (heat, work, mass transfer) must be equal to the amount of energy leaving it for a steady-flow process. In an equation format, it is
(Rate of net energy transfer in by heat, work and mass) =(Rate of net energy transfer out by heat, work and mass)
Or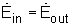 
For a general steady-flow process, the energy balance can be written as
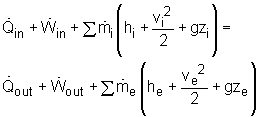
If the sign introduced previously for heat and work is used, the energy balance for a general steady-flow process can be rewritten as:
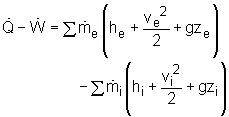
Key points
1) The total amount of mass contained within a control volume does not change with time. That is,
Dmsystem/dt = 0
There are a number of steady flow engineering devices. For instance there are nozzles and diffusers, as well as pumps and compressors.
First, during a steady flow process, the fluid will flow through the control volume steadily. As a result, the mass flow will be constant. In addition, during a steady state process any intensive or extensive properties will remain constant. Hence, specific volume, internal energy, etc would remain constant at a specified point. This doesn’t mean it can’t be different at different points within the system. Refer to the equation below.
(Eq1)
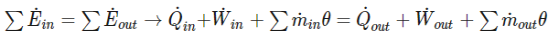
Q˙ = Rate of Heat Transfer
W˙ =Rate of Work
m˙ = mass flow
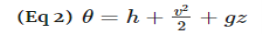
h = enthalpy
v = velocity
g = gravitational constant
z = elevation
Finally, the boundary work has to be zero. This doesn’t mean that there can’t be other aspects that require work, or produce work. For example shaft work is required to turn the blades of a turbine.
Steady Flow Engineering Devices
For a device to be considered a steady flow device it must be able to operate under the same conditions for a long period of time. There are a number of steady flow devices. For instance there are Nozzles & Diffusers, Turbines & Compressors, Throttling Valves, and Heat Exchangers & Mixing Chambers.
Nozzles & Diffusers
Nozzles are steady flow engineering devices that are used to increase a fluids velocity at the expense of pressure. For subsonic flows a nozzle will have a wider cross-sectional area at its entrance. The cross-sectional area will slope to a smaller cross-sectional area at its exit. On the other hand when the flow is supersonic, the entrance cross-sectional will be smaller than the exit cross-sectional area. The image below shows a basic subsonic nozzle.
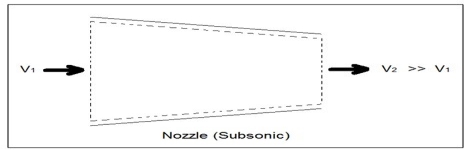
Fig 3
A diffuser is the exact opposite of a nozzle. Unlike a nozzle, it is used to decrease a fluids velocity. For subsonic flows the entrance of a diffuser is larger than its exit. In contrast, for supersonic flows the entrance is smaller than its exit. The image below shows a basic subsonic diffuser.
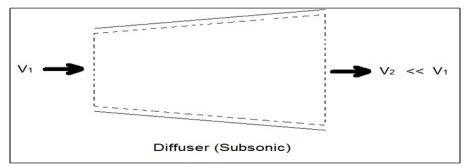
Fig 4
For both nozzles and diffusers, the rate of heat entering or exiting the boundary layer can be considered zero. In addition, the work and potential energy can also be considered zero. Taking these factors into consideration the energy balance equation for a nozzle and diffuser will be the following.
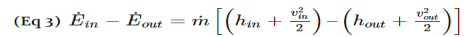
Turbines
Turbines are steady flow engineering devices that rely on shaft work to drive an electric generator. They are found in steam, gas, and hydrostatic power plants. Heat transfer is negligible. In addition, potential energy is negligible unless otherwise stated. Finally, even though kinetic energy is present within the system, the change in enthalpy is normally much greater. As a result, kinetic energy is also negligible.
During operation super-heated steam will be pushed through the turbine. As this is occurring it is possible that the steam could become a saturated gas when it leaves. This must be taken into consideration when you are calculating the exit enthalpy. Finally, liquids can damage the blades of a turbine. As a result, it is best to keep a fluid in a gas state as it passes through the turbine.
The equation below represents the basic energy balance for a turbine.
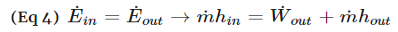
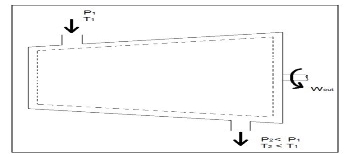
Fig 5
Compressors
A compressor, unlike a turbine, is a steady flow engineering device that uses shaft work to create power. Hence, shaft work is required to run a compressor. In addition, heat transfer, as well as potential and kinetic energy are negligible. The equation below represents the basic energy balance for a compressor.
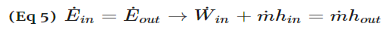
Fig 6
Other devices that are similar to compressors are fans and pumps. There are, however, some application differences between these devices. For instance, a fan does not raise the pressure of a fluid to a high pressure. Instead it will mobilize a gas. Pumps, on the other hand, are used to move or pressurize liquids. Pumps can only be used for liquids, while compressors can only be used on gases. If a pump tried to pump a gas it could be damaged. The same goes for a compressor if it were used to compress a liquid it would most likely ruin the compressor.
Throttling Valves:
A throttling valve is a steady flow engineering device that is used to restrict flow. A considerable pressure drop will result from the restricted flow. In turn, a large temperature drop will result. Hence, throttling valves are widely used in refrigeration devices. There are many devices that can be considered throttling valves. Some examples are porous plugs, capillary tubes, and adjustable valves.
Fluid flowing through a throttling valve undergoes an adiabatic process. In addition, no work is done and potential energy is negligible. Kinetic energy is also negligible even though there is a large change in velocity. Instead change in internal energy is much more pronounced in comparison to kinetic energy. Finally, enthalpy values at the entrance and exit of the throttling valve are approximately the same. Taking all of this into consideration the following energy balance equation for a throttling valve will result.
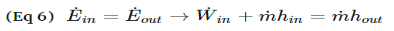
Types of Throttling Valves
Throttling valves are very simple steady flow engineering devices. As mentioned above throttling valves can be a porous plug, capillary tubes put in between two large tubes, or simply an adjustable valve like a ball valve. The whole point is to restrict the flow to drastically drop the pressure which will cause a large temperature drop within the fluid. Refer to the image below to see different types of throttling valves.
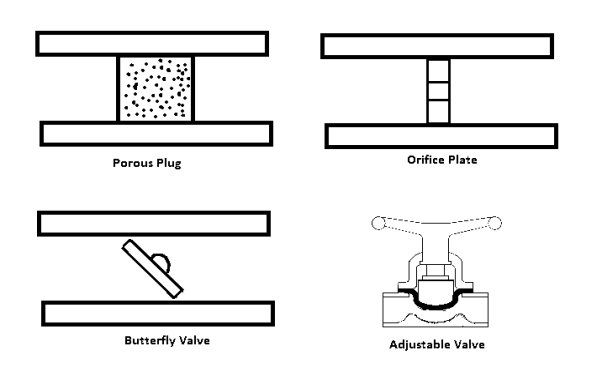
Fig 7
For a fun fact, besides refrigerators, another common device that uses a throttling valve is the carburettor in a small engine. The throttling valve in a small engine is not there to adjust the temperature of the gas. Instead it is used to control the amount of air that will mix with the gas to control combustion. If there isn’t enough air, the engine will run rich causing poor fuel economy. On the other hand, if there is too much air, the engine will run lean. This will cause the engine to produce more heat. As a result, less power will be produced.
The type of valve used on carburettors is typically a butterfly valve. The throttling valve is normally controlled by the choke. Closing the choke purposely causes the engine to run rich. This is done to make it easier to start the engine. The choke is than opened to allow optimal running conditions once the engine has warmed up. The stoichiometric air-fuel ratio which 14.7 lb of for ever 1 lb of fuel is the ideal air to fuel ratio for lowest emission, however, the best ratio for power is 12.5 lb of air for 1 lb of fuel.
Mixing Chambers
Mixing chamber are steady flow engineering devices that mix two streams of fluid to cause a temperature change. The temperature alteration is highly dependent on the mass flow of the two streams in comparison to each other.When solving for these types of problems the conservation of mass must be taken into consideration. For this device the mass of fluid entering must equal the mass of fluid exiting. In addition, how well insulated the device is must be considered. A well-insulated device will have negligible heat transfer to the outside environment. Finally, both potential and kinetic energy are negligible. Taking all of this into consideration the following energy balance is used for a well-insulated mixing chamber.
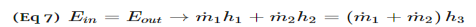
Fig 8
Heat Exchangers
Heat exchangers are similar to mixing chambers except they do not allow the two streams of fluid to mix. As a result, the mass flow entering each pipe will remain constant. In addition, for well insulated heat exchangers heat transfer can be considered negligible. In addition, kinetic and potential energy as well as work is negligible. The following energy balance equation is used for a well insulating heat exchanger.
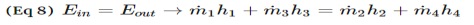
This equation is meant for a heat exchanger scene in the image below. If the heat exchanger you are looking at is different you may have to modify equation 8.
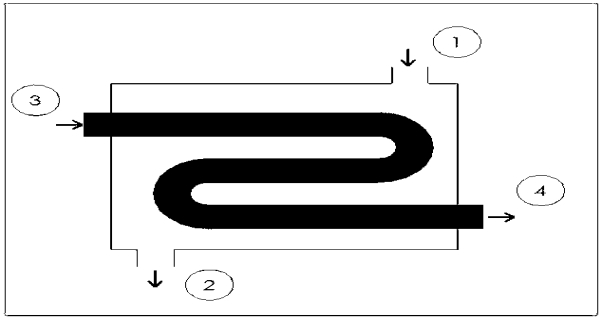
Key points
1) Energy balance equation for a nozzle and diffuser will be the following.
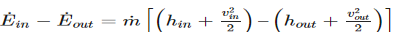
2) Energy balance equation is used for a well insulating heat exchanger.
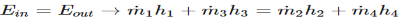
3) Energy balance is used for a well-insulated mixing chamber.
|
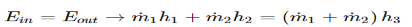
Noted that nozzles, diffusers, turbines, compressors and other devices undergo a steady-flow process because of their long-time running considerationBut their start up and shutdown periods undergo transient operations since their states change with time. The flow processes involved are called unsteady-flow processes, or transient-flow processes. Unlike steady-flow processes, unsteady-flow processes start and end over some finite time period (Δt). An additional example of an unsteady-flow process is filling or discharging a tank.
During an unsteady-flow process, the mass in the control volume changes with time. The mass balance for a system undergoing any process, can be used for control volume as
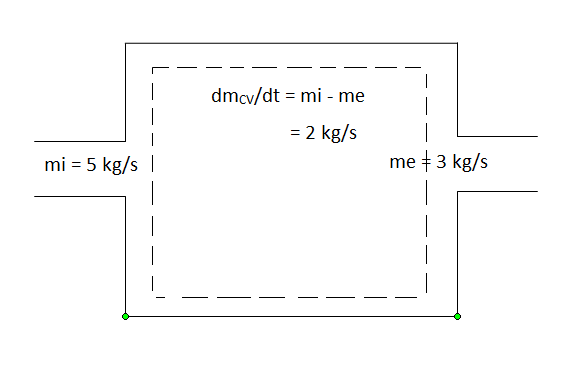
Fig 10
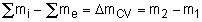
Where
i = inlet
e = exit
ΔmCV = mCVfinal - mCVinitial
mi = the mass flow into the control volume
through one inlet
me = the mass flow out of the control volume
through one exit
Or in rate form
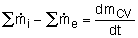
where
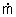i = the rate of mass flow into the control
volume through an inlet
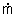e = the rate of mass flow out of the control
volume through an exit
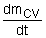= the rate of change of mass within the
control volume
Also, the energy content of a control volume changes with time during an unsteady-flow process. The general energy balance can be used for the control volume as
Ei - Ee = ΔECV
Where
Ei = the total energy transferred into the control
volume by heat, work, and mass
Ee = the total energy transferred out of the control
volume by heat, work, and mass
ΔECV = energy change in the control volume in
forms of internal, kinetic, potential, etc.,
energies
Or in rate form
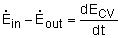
Where
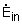= rate of energy transferred into the control
volume by heat, work, and mass
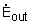= rate of energy transferred out of the
control volume by heat, work, and mass
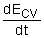= rate of energy change in the control
volume in forms of internal, kinetic,
potential, etc., energies
Noting that the energy can be transferred by heat, work, and mass only, the energy balance can be rewritten as
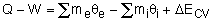
Where
θ = h + v2/2 + gz
The total energy of a flowing fluid per unit mass
ΔECV = (ΔU + ΔKE + ΔPE)CV
During a steady-flow process, no changes occur within the control volume; thus, one does not need to be concerned about what is going on within the boundaries. Not having to worry about any changes within the control volume with time greatly simplifies the analysis.
Many processes of interest, however, involve changes within the control volume with time. Such processes are called unsteady-flow, or transient-flow, processes. The steady-flow relations developed earlier are obviously not applicable to these processes. When an unsteady-flow process is analysed, it is important to keep track of the mass and energy contents of the control volume as well as the energy interactions across the boundary.
Some familiar unsteady-flow processes are the charging of rigid vessels from supply lines discharging a fluid from a pressurized vessel, driving a gas turbine with pressurized air stored in a large container, inflating tires or balloons, and even cooking with an ordinary pressure cooker.Unlike steady-flow processes, unsteady-flow processes start and end over some finite time period instead of continuing indefinitely. Therefore in this with the rate of changes (changes per unit time). An unsteady-flow system, in some respects, is similar to a closed system, except that the mass within the system boundaries does not remain constant during a process.
Another difference between steady- and unsteady-flow systems is that steady-flow systems are fixed in space, size, and shape. Unsteady-flow systems They are usually stationary; that is, they are fixed in space, but they may involve moving boundaries and thus boundary work.
Key points
1) The energy balance can be rewritten as
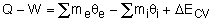
Where
θ = h + v2/2 + gz
2) The total energy of a flowing fluid per unit mass
ΔECV = (ΔU + ΔKE + ΔPE)CV
Reference:
- Engineering thermodynamics
- ASHRAE, Air Conditioning System Design Manual, IInd edition, ASHRAE.
- Thermodynamics P.K Nag
- Threlkeld J.L., Thermal Environmental Engineering, Prentice Hall Inc. New Delhi
