Unit – 2
Curves
(a) Linear method
(i) Offset from long chord
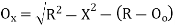
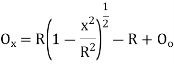
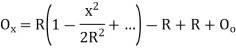
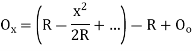
Where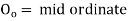 
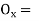offset at some point P at distance x from midpoint D.
(ii) Perpendicular offset from tangent
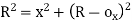
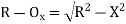
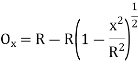
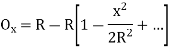
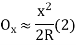
(iii) Radial offset from tangent:
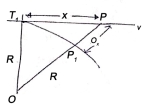
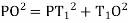
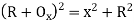
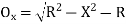
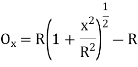
(iv) Successive Bisection of Arc or chord
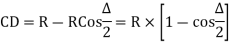
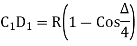
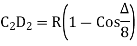
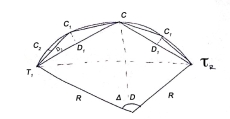
(v) By offset from chord produced
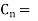last sub chord
b) Angular method
i) Rankine's method of deflection angle
- It is generally used for setting out a circular curve of long length and large radius.
- It gives good result except then chords are long as compared to radius, so that variation between length of an Arc and its cord becomes considerable.
- It is used in highway and Railway
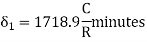
= Tangential angle
C = chord length
(ii) Tachometric method
-It is similar to Rankine’s method of deflection angle.
- The theodolite at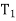 
may be used as Tacheometric and Tacheometric observation are made.
- Less accurate as compared to Rankins.
- Chaining is completely dispersed in this method.
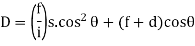
(For Incline and line of sight)
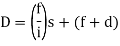
(For horizontal line of sight)
ii) Two theodolite method
- Convenient than any of to our method when ground is undulating rough and not suitable for Linear measurements.
- Two theodolites are used and linear measurement are completely eliminated.
- Hence, most accurate method.
- It is based on principle that angle between the tangent and chord is equal to angle subtended by chord in opposite segment.
- Time consuming method
- Most accurate method
- Highly expensive.
Reverse curve: -
When to normal circular curves of different or equal radii, have opposite in direction of curvature join together, the formed or resultant curve is known as reverse curve.
Uses: -
a) When angle between two straight line is very small.
b) When two straight line are parallel to each other.
Element of reverse curve
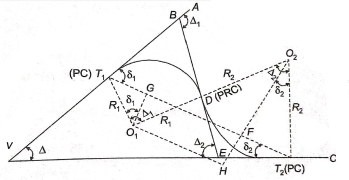
- VA and ucinclude deviation angle of
.
- 
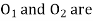centres of two curves.
- 
are radii of two curve.
- 
common tangent which is perpendicular to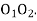 
- Join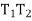 
and draw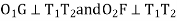 
In ∆BVE,
In 
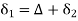
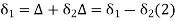
From (1) and (2)
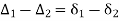
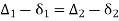
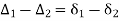
In,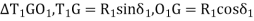 
In,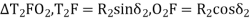
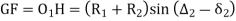
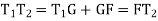
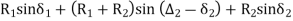
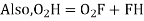
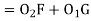
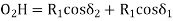
Also,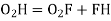
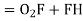
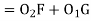
From (3) and (4)
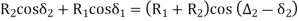
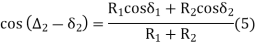
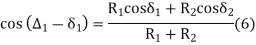
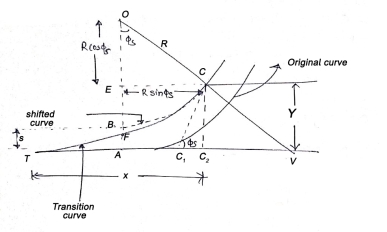
- It is a curve introduced between a simple circular curve industry tour between two simple circular curves.
- Also known as easement curve.
- Its videos, gradually changing from a finite to infinite value or vice versa.
- It is generally used in highway and Railway.
Length of transition curve: -
a) Method of arbitrary gradient: -
e = total super elevation provided at junction of transition curve with circular curve
L = ne
Where rate of super elevation is ∆ in n
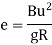
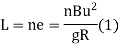
(b) Method of Time rate: -
time rate of super elevation
Method of rate of change of radial acceleration
Rate of change of radial acceleration
t is the time attained by radial acceleration (a)
a =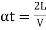 
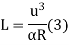
Super elevation or Cant:
It is defined as the raising of outer end of a road or outer rail over inner one.
h = super elevation = e
w = weight of vehicle
P = centrifugal force
g = acceleration due to gravity
R = radius of curve
G = gauge distance between rails
u = speed of vehicle
B = width of pavement
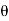= Angle of super elevation
h = super elevation = e
w = weight of vehicle
P = centrifugal force
g = acceleration due to gravity
R = radius of curve
G = gauge distance between rails
u = speed of vehicle
B = width of pavement
= Angle of super elevation
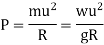
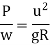
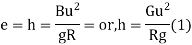
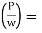Centrifugal ratio
Formula for elements of a simple circular curve
a) Relation between degree and radius of curve.
Arc definition / Chord Definition: -
Arc definition of degree of curve: According to this, degree of curve in the central angle subtended by an arc of length of 20m or 30 m.
If R = radius of curve
D = degree of curve as per arc definition for 30m arc length.
D° =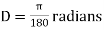 
Q (radians) =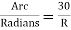 
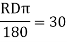
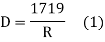
For 20 mm length
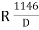(2)
(b) length of curve
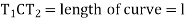
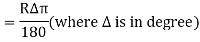
If a 30m arc or chord definition is used
If a 20 m arc or chord definition is used.
(c) Length of tangent: -
Tangent length (T) =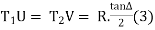 
(d) long chord length
Length of long chord (L)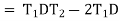 
From 
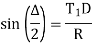
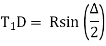
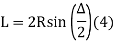
(e) Apex distance: -
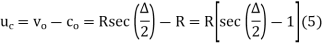
(f) Mid ordinate: -
(a)Total Tangent Length
Tangent length 
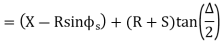
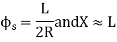
(b) Length of long chord
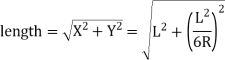
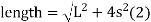
(c) Total length of curve
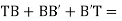Total length of curve
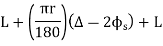
=Total length (3)
(d) Apex distance E
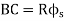
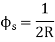
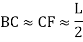
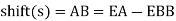
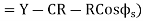
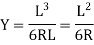
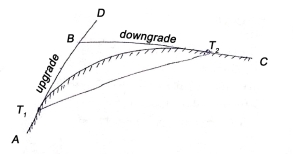
These are curves in a vertical plane, used to join two intersecting grade lines.
A vertical summit curve is provided when a rising grade join a falling grade and a vertical curve is provided when a falling grade joins a rising grade.
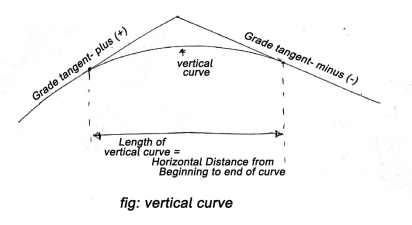
PVC – point of vertical curvature place where curve begins
PVT – point of vertical tangency, where curve end.
PVI – point of vertical intersection, where grade tangents intersect.
POVC - point on vertical curve applies to any point on parabola
POVT - point on vertical tangent, applies to any point on other tangent
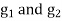are grade tangent at PVC and PVT respectively.
(a) Length of vertical curve
L = algebraic difference of two grades/ rate of change of grade
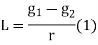
(b) Change of end of curve
PVT = change of intersection point + half the length
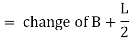
Types of vertical curves
iii) Upgrade followed by a downgrade
iv) Upgrade followed by another upgrade
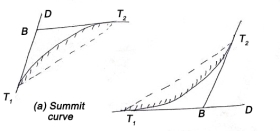
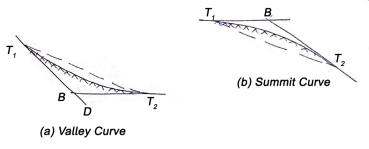
v) A downgrade followed by an upgrade
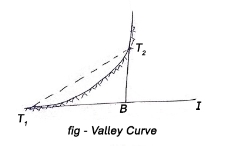
vi) A downgrade followed by another downgrade
References:
1 Madhu, N, Sathikumar, R and Satheesh Gobi, Advanced Surveying: Total Station, GIS and Remote
Sensing, Pearson India, 2006.
2 Manoj, K. Arora and Badjatia, Geomatics Engineering, Nem Chand & Bros, 2011
3 Bhavikatti, S.S., Surveying and Levelling, Vol. I and II, I.K. International, 2010 4 Chandra, A.M., Higher
Surveying, Third Edition, New Age International (P) Limited, 2002.
5 Anji Reddy, M., Remote sensing and Geographical information system, B.S.
6 Arora, K.R., Surveying, Vol-I, II and III, Standard Book House, 2015.
