Unit - 5
Periodic properties
Effective Nuclear charge
The term effective Nuclear charge is the net total charge that an electron experiences in an atom in the presence multiple electrons. The effective nuclear charge may be estimated by the equation:
Zeff = Z - S
Where Z is the atomic number and S is the number of shielding electrons.
Electrons of higher can possess different electrons of lower energy between the electron and the nucleus, thereby lowering the positive charge experienced by the high energy electron.
The shielding effect is named as it gives a balance between the repulsion between valence and inner electrons the attraction of valence electrons. The shielding effect also explains the trend in atomic size followed in the periodic table and also explains why valence electrons are readily removed from an atom.
Penetration of orbitals
It is the ability of an orbital to attract an electron. This process is achieved together with release of energy. The high extent of penetration is a feature of orbitals. The penetration effect of S orbital is the maximum because of the closeness to the nucleus that are the p, d and f orbitals. It describes the proximity to which an electron can approach to the nucleus. In a multi electron system electron penetration is defined by an electron’s relative electron density near the nucleus of an atom. Electrons in different orbitals have different electron densities around the nucleus.

Fig. 1: Orbital Penetration.
The figure shows a distribution of radial probability of the 2p and 2s orbitals for various states of the hydrogen atom shows that the 2s orbital penetrates more inside the 1s orbital more than the 2p orbital. Subsequently, when an electron is in the small inner lobe of the 2s orbital, it experiences a comparatively large value of Zeff, which causes the energy of the 2s orbital to be lower than the energy of the 2p orbital.
Variation of s, p, d and f orbitals energies of atoms in the Periodic Table
Orbitals are regions of space where electrons are most likely to be found in an atom. These orbitals are designed as s, p, d, f among others. The energy increases as you move up the orbital in such a way that S orbital has the lowest energy and f orbital has highest energy as the energy levels increases the electrons are located further away from the nucleus.
S-orbitals
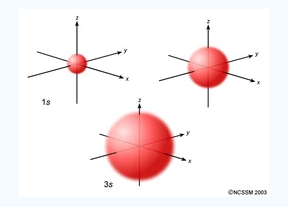
An S orbital is spherical symmetrical around the nucleus of an atom like a hollow ball with nucleus at the centre. As the levels of energy increase, the electrons are located further away from the nucleus, so the orbitals get bigger the order of size is
1s<2s<3s< ------ as shown
Fig.2: The figure shows that as the energy levels increase, the electrons move further away from the nucleus, as a result the orbitals get bigger in size the order of size is 1s<2s<3s<…
p orbitals
Unlike s orbitals, a p orbital points in a particular direction, at any one energy level we have three absolutely equivalent p orbitals pointing mutually at right angles to each other they are given symbols px, py, pz. The p-orbitals at the second energy level are called 2px, 2py,2pz and so on. All levels except the first energy level have p orbitals.
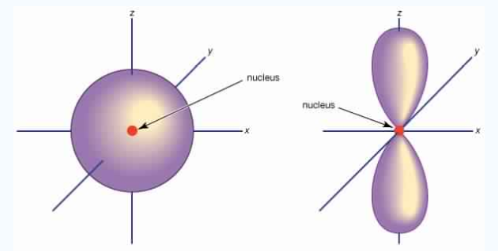
Fig.3: At any one energy level, we have absolutely three equivalent p orbital pointing
mutually at right angles to each other, They are arbitrarily given the symbols px, py, pz.
At any one energy, we have three absolutely equivalent p orbitals pointing mutually at right angles to each other. These are arbitrarily given the symbols px, py, pz, which is for convenience. the p orbitals at the second energy level are called 2px,2py,2pz. there are similar orbitals at subsequent levels: 3px,3py,3pz….and 4px, p4py,4pz and so on. All levels except the first have p orbitals.

Fig.4: In addition to s and p orbitals, there are two other sets of orbitals which become available for electrons to inhabit at higher energy levels, at the third level, there are a aet of five d orbitals as well as 3s and 3p orbitals, at the third level there are a total of nine orbitals.
d orbital
In addition to s and p orbitals, there are 2 other sets of orbitals which are available for electrons to inhabit at higher energy levels as well as the 3s and 3p orbitals at the third level there are now a total of nine orbitals altogether.
3dxy, 3dxz, 3dyz, 3dx2-y2, 3dz2

Fig. 5: The first group contains 3dxy,3dxz and3dyz orbitals, the names specify that these orbitals Lie in the x-y plane, the x-z plane and the y-z plane. Each lobe has four lobes and each lobe points between. Two axes and not along them. The second group contains the 3dx2-y2and3dz2 orbitals, these lobes point along various axes the 3dx2-y2 looks exactly like the first group, except that the lobes are pointing along. The x and y axes, not between them. The3dz2 looks like a p orbital...:
f orbital
At the fourth and higher levels there are 7f orbitals in addition to the 4s, 4p and 4d orbitals. Counting the 4s, 4p and 4d orbitals. This makes a total of 16 orbitals in the 4th level.
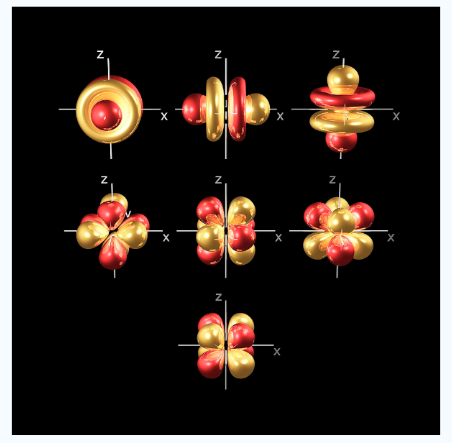
Fig.6: counting the 4s,4p,4d orbitals, this makes a total of 16 orbitals in the fourth level. The s, p, d and f orbitals are more complicated at higher energy levels.
Electron Configuration
Electron configuration holds the key to the chemical world. Our generation understands the chemical properties of organic and inorganic compounds based on the electronic configuration of the constituent elements.
Therefore, in a reaction the chemical bonding is the arrangement of electrons of reactant atoms. Classification of periodic table is based on the electron configuration of the elements.
The 3S orbital has lower energy than 3P orbitals which again has a lower energy than 3d orbitals. But the orbitals belonging to a particular type (P or d or f) will have an energy equal of an atom or an ion.
Rules for writing electronic configuration
The electron configuration of elements or its ions should be according to the following rules
Where l = 0, 1, 2, 3 for s, p, d, f orbitals respectively.
Electron configuration and energy levels
An easy way to remember these energy levels is provided below this diagram
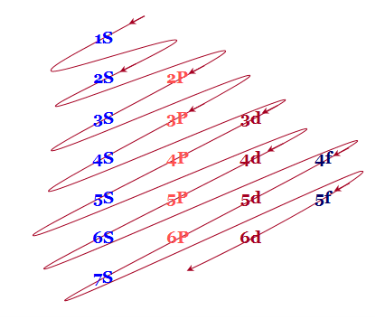
Fig.7: The figure shows an increase in energy every orbital. S orbital have the lowest energy, energy continuously increases in each block as we move, downward in group of left to right across the period.
Electron shells
According to this diagram, the energy levels are
1S < 2S < 2P < 3S < 3P < 4S < 3d < 4P < 5S < 4d < 5P < 6S < 4f < 5d < 6P < 7S < 5f…
Pauli exclusion principle
Pauli exclusion principle uses for the pictorial representation of electron configuration.
No two electrons of the atom can have similar four quantum numbers.
An alternative statement of Pauli’s exclusion principle, not more than two electrons can be placed in only one and same orbital.
When an orbital contains two electrons, the electrons are paired. These two electrons per orbital given the maximum place for electrons.
Periodic table and electronic configuration
Extranuclear electrons are responsible for the chemical action of elements and periodic classification of the elements are also based on the chemical behavior.
Thus, the electronic configuration of elements must be related with the periodic table. Especially, the arrangement of the electrons in the outermost orbitals detects the position of the elements in the periodic table.
Atomic radii or size can be defined in the most simplified manner as the radii (or half the "width") of the spherical atoms. Nonbonding atoms have a much larger, more indefinite or "fuzzy" radius, therefore when atomic radius is described as a periodic trend, the thing that comes to mind is bonding atomic radius.
These are the radii of atoms that are chemically bonded to each another. So, if the bond between two Cl atoms in Cl2 is 1.99 angstroms, resulting in chlorine's bonding atomic radius as about 0.99 angstrom. These values are then used to estimate bond lengths between different elements in molecules.
Atomic radius generally increases from top to bottom down a group. This generally occurs due to the increase in the principal quantum number, (n). Therefore, when we go further down a column, the outer electrons move much further away from the atom, making the atom thus larger.
Generally, the atomic radius decreases as we move from left to right across a period. This occurs mainly due to effective nuclear charge. The greater the effective nuclear charge, the more will be the attraction felt by the outer electrons from the nucleus, and the closer the outer electrons are to the nucleus, making the atom smaller.
Ionic Size
Ionic radii are the radii of ions of elements. These distances are based on distances that exist between ions in ionic compounds.
Cations, or positively charged ions, are smaller in size than their "parent" atoms. This is because cations are formed when the outermost orbitals become empty due to absence of electrons. This also decreases electron-electron repulsions. Therefore, the resulting ions are smaller as there are not as many orbitals that are occupied and the effective nuclear charge affecting the remaining electrons increases, pulling electrons in more closely.
Anions, or negatively charged ions, are larger in size than their "parent" atoms. This is because of the addition of electrons form these ions, increasing electron-electron repulsions, making the electrons spread out more effectively. Also, effective nuclear charge felt by the outermost electrons decreases. For ions that carry the same charge (i.e., from parent elements of the same group), size increases from top to bottom as we go down a group.
Ionization Energy
The ionization energy of a chemical category (i.e., an atom or molecule) is the energy required to remove electrons from gaseous ions or atoms. This property is also referred to as the ionization potential and is measured in volts. In chemistry, it often refers to one mole of a substance (molar ionization energy or enthalpy) and is reported in kJ/mol. In atomic physics, the ionization energy is typically measured in the unit electron volt (eV). Atoms or molecules which are larger have lower ionization energy, while smaller molecules or atoms tend to have higher ionization energies.
The ionization energy is not the same for electrons of different molecular or ionic orbitals.
More specifically, the nth ionization energy is the energy required to eliminate the nth electron after the first n-1 electrons are removed. It is perhaps a measure of the tendency of an ion or atom to surrender an electron or the strength of the electron binding. The greater the ionization energy, the more difficult to remove an electron. The ionization energy may be an indicator to show the reaction of an element. Elements with a lower ionization energy tend to be reducing agents and form cations, and thereby combine with anions to form salts.
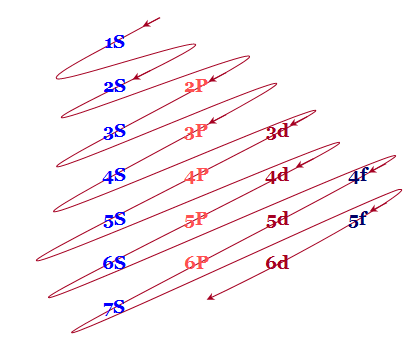
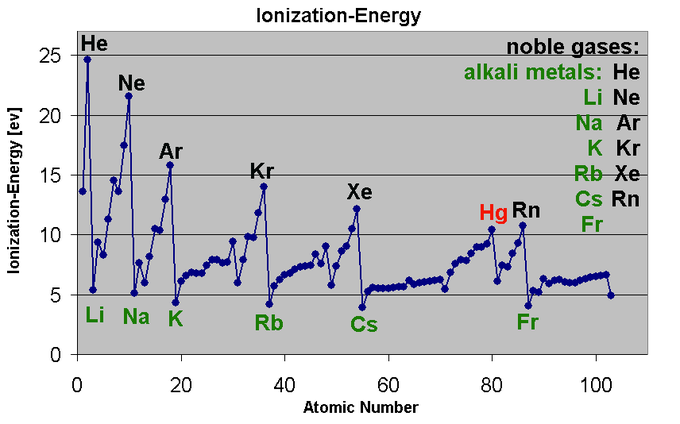
Fig.8: This graph shows the first ionization energy of the elements in electron volts(units).
Moving from left to right within a period or upward within a group, the first ionization energy shows an increase. As the atomic radius of an ion or atom reduces, it becomes difficult to remove an electron that is close to a more positively charged nucleus. On the other hand, as one moves down a group on the periodic table, the ionization energy will likely decrease since the valence electrons are far away from the nucleus and experience greater shielding. They experience a weaker attraction to the positive charge of the nucleus. Ionization energy increases when viewed from left to right in a specific time and decreases from top to bottom in a group.
Rationale for the Periodic Trends in Ionization Energy
The ionization energy of an element shows an increase as one move across the periodic table because the electrons are held together tightly by the highly effective nuclear charge. This is due to the additional electrons in the same shell do not substantially contribute to shielding each other from the nucleus, however an increase in atomic number corresponds to an increase in the number of protons in the nucleus.
The ionization energy of the elements shows an increase as one moves up a given group because the electrons are held in lower-energy orbitals, closer to the nucleus and thus more tightly bound (which is difficult to remove). The easiest element to ionize is francium and the hardest to ionize is helium respectively. Cesium is said to have the lowest ionization energy and Fluorine is said to have the highest ionization energy (with the exception of Helium and Neon).
Electron affinity reflects the ability of an atom to accept an electron. It is the energy change which occurs when an electron is added to a gaseous atom. Atoms with strong effective nuclear charge have greater electron affinity.
The reaction that occurs when an atom takes an electron may be represented as:
X + e− → X− + energy
Another way to define electron affinity is as the amount of energy needed to remove an electron from a singly charged negative ion:
X− → X + e−
Key Takeaways:
Electron Affinity Definition and Trend
Electron Affinity Trend
Electronegativity
Electronegativity is the property of an atom which increases with its tendency to attract the electrons of a bond. when two bonded atoms that have similar electronegativity values as each other, they share electrons equally in a covalent bond. Usually, the electrons present in a chemical bond are more attracted to one atom (the more electronegative one) than to the other one. This results in a polar covalent bond. If the electronegativity values are very different, the electrons do not show any sharing. One atom essentially takes the bond electrons from the other atom, forming an ionic bond.
Electronegativity is a property of an atom present within a molecule, rather than a fundamental property of an atom by itself. Thus, electronegativity varies depending on an atom's environment or surroundings. However, most of the time an atom displays similar behaviour in different situations. Factors that affect electronegativity include the nuclear charge and the position and number of electrons in an atom.
Electronegativity Example
The chlorine atom has a higher electronegativity than the hydrogen atom, so the bonding electrons will be closer to the Cl than to the H in HCl molecule.
In the O2 molecule, both atoms have the same electronegativity. The electrons in the covalent bond are shared equally between the two oxygen atoms.
Polarizability
The polarizability of a molecule is a measure of the ability of the molecule to respond to an electric field and obtain an electric dipole moment p. There are many microscopic mechanisms of polarization in a dielectric material. The Electric dipole moments may be permanent or may be induced by an electric field.
The induced electric dipole moment can be achieved as a result of two polarization phenomena, i.e., electronic polarization and distortion polarization.
Electronic polarization, αe, describes the shift of the cloud of bound electrons with reference to the nucleus under an applied electric field. The atom scatter, and the center of the atom’s negative charge eventually does not coincide with the position of the nucleus, resulting in an electric dipole moment. The electric dipole moment of each atom is described by
p=αeE*
Distortion polarization αd (also often referred to as ionic polarization) relates to the distortion of the position of the nuclei by the applied field, resulting in stretching or compressing the bond length, depending on the relative orientation between the electric field and ionic bond. The molecule is stretched and bent by the applied field and accordingly changes its dipole moment. Nonpolar molecules may acquire an induced dipole moment in an electric field as a result due to the distortion of the electric field that causes disturbance in electronic distributions and nuclear positions. A polar molecule is one with a permanent electric dipole moment. The permanent dipole moment is formed due to the partial charges on the atoms in the molecule that emerge from the different electronegativity or other features of bonding. Polar molecules may possess their existing dipole moments modified by the applied field. Orientation polarization identifies with the phenomenon of a permanent dipole moment as a result of polar molecules. The total polarization of a medium, composed of polarizable polar molecules, is therefore
P=N(αe+αd+μ23kT) E*
where N is the number of molecules per m3, μ is the orientation polarizability, k is the Boltzmann constant, and T is the temperature in K.
The terms αe and αd represent the electronic and distortion polarization in the molecule, while the term μ2/3kT stems from the thermal averaging of permanent electric dipole moments in the presence of an applied field. The quantitative relation between the relative permittivity and properties of the molecules is described by the Debye equation:
εr−1εr+2=N3ϵ0(αe+αd+μ23kT)
The relative permittivity εr of materials is high if its molecules are polar and highly polarizable. This equation shows that the permittivity is smaller if materials do not contain polar molecules. The reduction of density polarizabilities αe and αd and N are also possible ways of decreasing the dielectric constant. Reducing the number of ionic bonds in the material minimizes distortion polarization. The electronic polarization is minimized by lowering the electron density in the material, i.e., introducing smaller elements. The same expression, but without the permanent dipole moment contribution, is called the Clausius–Mossotti equation:
εr−1εr+2=N3ε0(αe+αd)
Although the value of the electric dipole moments is extremely important for predicting properties of dielectric materials, their calculation becomes difficult. In the case of simple molecules, the Stark effect is used to measure the electric dipole moment of molecules for which rotational spectra can be observed. In the case of more complicated cases, the permanent dipole moment and polarizability of molecules can be calculated by measuring εr at a series of temperatures. These measurements make it easy to determine the molar polarizations and their slope and intersect versus 1/T give values of dipole moment and polarizability.
Acids and Bases
For thousands of years people have known that vinegar, lemon juice, and many other foods taste sour. eventually, it was not until a few hundred years back that it was discovered why these foods taste sour – because they are all acids. The term acid, in fact, comes from the Latin term acere, which means "sour". While there may be different definitions of acids and bases, In the seventeenth century, An Irish writer and amateur chemist Robert Boyle first labelled substances as either acids or bases (he called bases alkalies), according to the following characteristics:
Acids: Acids become less acidic when mixed with bases they taste sour, are corrosive to metals, change litmus (a dye extracted from lichens) to red.
Bases: feel slippery, change litmus blue, and become less basic when mixed with acids.
While Boyle and others failed to explain why acids and bases behave the way they do, the first reliable definition of acids and bases was not be proposed until 200 years later.
In the late 1800s, the Swedish scientist Svante Arrhenius suggested that water can dissolve many compounds by separating them into their individual ions. Arrhenius suggested that acids are compounds that contain hydrogen and can dissolve in water to release hydrogen ions into a solution. For example, hydrochloric acid (HCl) dissolves in water as follows:
HCl H2O→ H+(aq) + Cl-(aq)
Arrhenius defined bases as those substances that can dissolve in water to release hydroxide ions (OH-) into the solution. For example, a typical base, sodium hydroxide (NaOH) was suggested by Arrhenius:
NaOH H2O→ Na+(aq) + OH-(aq)
The Arrhenius definition of acids and bases explains many things about Acids and Bases. Arrhenius's theory corelates how all acids have similar properties to each other (and, conversely, why all bases are similar): since all acids release H+ into solution (and all bases release OH-). The Arrhenius definition clearly explains Boyle's observation that bases and acids counteract each other. This idea, that a base can make an acid weaker, and that an acid can make a base weaker, is called neutralization.
Neutralization
As you can see from the equations, acids release H+ into solution and bases release OH-. If we were to mix an acid and base together, the H+ ion would combine with the OH- ion to make the molecule H2O, or plain water:
H+(aq) + OH-(aq) → H2O
The neutralization reaction of an acid with a base will always form water and a salt, as shown below:
Acid Base Water Salt
HCl + NaOH → H2O + NaCl
HBr + KOH → H2O + KBr
Though Arrhenius helped explain the fundamentals of acid/base chemistry, unfortunately his theories have limits. For example, the Arrhenius definition does not explain why some substances, such as common baking soda (NaHCO3), this compound act like a base even though they do not contain hydroxide ions.
In 1923, the Danish scientist Johannes Brønsted and the Englishman Thomas Lowry published an independent but similar paper that was defined in Arrhenius' theory. According to Bronsted’s, "... acids and bases are substances that are capable of releasing or taking up hydrogen ions, respectively." The Brønsted-Lowry definition has a widespread concept of the Arrhenius of acids and bases.
The Brønsted-Lowry definition of acids and bases is very similar to the Arrhenius definition: Any substance that can release a hydrogen ion is an acid. (According to the Brønsted definition, acids are seldom mentioned to as proton donors because an H+ ion, hydrogen minus its electron, is simply a proton).
The Brønsted definition of bases is, however, very different from the Arrhenius definition. The Bronsted theory of base is defined as any substance that can concede a hydrogen ion. In other words, a base is the opposite of an acid. NaOH and KOH, as seen above, would still be considered bases because they can accept an H+ from an acid to form water. However, the Brønsted-Lowry definition also explains the reasons why substances that do not contain OH- can still act like bases. Baking soda (NaHCO3), for example, acts like a base by accepting a hydrogen ion from an acid as illustrated below:
Acid Base Salt
HCl + NaHCO3 → H2CO3 + NaCl
In this example, the carbonic acid formed (H2CO3) undergoes rapid decomposition to water and gaseous carbon dioxide, and so the solution bubbles as CO2 gas are released.
pH
Under the Brønsted-Lowry definition, both acids and bases are related to the concentration of hydrogen ions present in the solution. Acids increase the concentration of hydrogen ions, while bases decrease the concentration of hydrogen ions (by accepting them). The acidity or basicity of a solution can be measured by its hydrogen ion concentration.
In 1909, the Danish biochemist Sören Sörensen invented the pH scale for measuring acidity. The pH scale is described by the formula:
pH = -log [H+]
For example, a solution with [H+] = 1 x 10-7 moles/liter has a pH equal to 7 (a simple way to think about pH is that it equals the exponent on the H+ concentration, without the minus sign). The pH scale has a range from 0 to 14. Substances that show a pH between 0 and less than 7 are acidic in nature (pH and [H+] are inversely related - lower pH means higher [H+]). Substances with a pH greater than 7 and up to 14 are basic in nature (higher pH means lower [H+]). Substances with a pH= 7, are neutral substances, for example, pure water.
Principle of HSAB theory
Ralph Pearson introduced the Hard Soft [Lewis] Acid Base (HSAB) principle in the early 1960s and made an attempt to unite inorganic and organic reaction chemistry. The impact of the new concept was immediate, however with the HSAB principle had rather fallen apart while other principles were introduced around the same time, such as frontier molecular orbital (FMO) theory and molecular mechanics, have flourished.
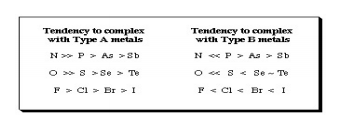
The Irving-Williams stability series (1953) had shown that for a given ligand the stability of dipositive metal ion complexes increases:
It was also found that a few ligands formed their most stable complexes with metal ions like Ti4, Al3+, and Co3+ while others were found to former stable complexes with Hg2+, Ag+ and Pt2+. In 1958 Ahrland et al. he had classified metal cations as Type A and Type B, where:
Type A metal cations included: Alkali metal cations: Li+ to Cs+, Alkaline earth metal cations: Be2+ to Ba2+, Lighter transition metal cations in higher oxidation states: Ti4+, Cr3+, Fe3+, Co3+ • The proton, H+
Type B metal cations include: • Heavier transition metal cations in lower oxidation states: Cu+, Ag+, Cd2+, Hg+, Ni2+, Pd2+, Pt2+. Ligands were classified as Type A or Type B depending upon whether they formed more stable complexes with Type A or Type B metals:
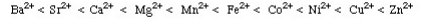
Fig.9: From this analysis, a principle was derived: Type A metals prefer to bind to Type A ligands and Type B metals prefer to bind to Type B ligands These empirical (experimentally derived) rules tell us that Type A metals are more likely to form oxides, nitrides, carbonates and fluorides, while Type B metals are more likely to form phosphides, selinides and sulphides. This pattern of analysis is importance economically because some metals are found in nature as sulfide ores: PbS, CdS, NiS, etc., while other are found in nature as carbonates: MgCO3 and CaCO3 and others as oxides: Fe2O3 and TiO2. This approach has been very successfully developed in last few years by Bruce Railsback. The Railsback analysis uses contours of behaviour overlapping upon the Mendeleev periodic table. Hard Soft [Lewis] Acid Base Principle In the early 1960s, Ralph Pearson developed the Type A and Type B logic by explaining in detail that the differential complex behaviour of cations and ligands in terms of electron pair donating Lewis bases and electron pair accepting Lewis’s acids: Lewis’s acid + Lewis base Lewis acid/base complex Pearson classified Lewis acids and Lewis bases as hard, borderline or soft.
Oxidation states
Oxidation state simplifies the whole process of working on what is being oxidised and being reduced in redox reactions. However, before the introduction, few things need to be known:
Let’s look at some examples from vanadium chemistry.
Vanadium forms a number of different ions - for example, V2+ and V3+. A doubt as to hoe these might be produced from vanadium metal, the 2+ ion will be formed as a result of oxidisation of the metal by removing two electrons:

The vanadium is now in an oxidation state of +2.
Further removal of another electron gives the V3+ ion:

The vanadium now has an oxidation state of +3.
Subsequently the removal of another electron gives a more unusual form of ion, VO2+.

The vanadium at present is in an oxidation state of +4. Therefore, the oxidation state is not counting the charge on the ion (which was true for the first two cases but not for this particular one).
The positive oxidation state is counting the total number of electrons which should have been removed - starting from the element.
In the next step it is also possible to remove a fifth electron to give another ion (this may be confused with the one before!). The oxidation state of the vanadium is now +5.

Every time you oxidise the vanadium by removing another electron from it, its oxidation state increases by 1.
If eventually electrons are added again the oxidation state will fall. And finally get back to the element vanadium where the oxidation state of zero.
What would be the case if we kept on adding electrons to the element? This cannot be done with vanadium, on the other hand with an element like sulphur.

According to this equation the sulphur compound has an oxidation state of -2.
Summary
Oxidation state shows the total number of electrons which have been added from an element (a negative oxidation state) or removed to an element (a positive oxidation state) to get to its present state.
Oxidation involves an increase in oxidation state
Reduction involves a decrease in oxidation state
This is a simple pattern and is the single most important thing about the concept of oxidation states. If the oxidation state of an element changes is known during a reaction, instantly it can be predicted whether it is being oxidised or reduced without having to work in terms of electron-half-equations and electron transfers.
Working out oxidation states
Oxidation states is not calculated by counting the numbers of electrons transferred. It would be a very long process. Instead, a few simple rules can be followed, and do some very simple sums!
Group 2 metals | always +2 |
|
Oxygen | usually -2 | except in peroxides and F2O (see below) |
Hydrogen | usually +1 | except in metal hydrides where it is -1 (see below) |
Fluorine | always -1 |
|
Chlorine | usually -1 | except in compounds with O or F (see below) |
Hybridization and Molecular Geometries
- A hybrid orbital or a mix of atomic orbitals
- An atomic orbital can interact with other atoms and overlap resulting in a given hybrid atomic orbital.
For example- here the sp hybrid atomic orbital is formed:

Fig.10: In picture, an atomic orbital can interact with other atoms and overlap resulting in a hybrid atomic orbital. The picture shows a sp hybrid orbital formed.
Molecular Orbitals
- single bonds are sigma bonds
- double and triple bonds each have one sigma bond
- double bonds have one pi bond
- triple bonds have two pi bonds
- there must be a sigma bond in order for a pi bond to occur
- Molecular Orbitals
Geometry
Bond | Hybridization | Geometry | Bond angle | Picture |
Single | sp3 | Tetrahedral | 109.5° |  |
Double | sp2 | Trigonal planar | 120° | 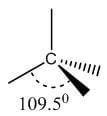 |
Triple | sp | Linear | 180° |
|
Bond | Hybridization | Geometry | Bond angle | Picture |
Single | sp3 | Tetrahedral | 109.5° |  |
Double | sp2 | Trigonal planar | 120° | 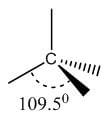 |
Triple | Sp | Linear | 180° | 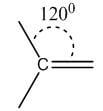 |
References:
1.The elements book – A visual encyclopaedia of the periodic table - Smithsonian
2. Essential textbooks in chemistry – Orbitals with application in Atomic Spectra – Charles. S. Mc Caw,
3. Atoms, electrons and change by Peter Atkins.
Unit - 5
Periodic properties
Effective Nuclear charge
The term effective Nuclear charge is the net total charge that an electron experiences in an atom in the presence multiple electrons. The effective nuclear charge may be estimated by the equation:
Zeff = Z - S
Where Z is the atomic number and S is the number of shielding electrons.
Electrons of higher can possess different electrons of lower energy between the electron and the nucleus, thereby lowering the positive charge experienced by the high energy electron.
The shielding effect is named as it gives a balance between the repulsion between valence and inner electrons the attraction of valence electrons. The shielding effect also explains the trend in atomic size followed in the periodic table and also explains why valence electrons are readily removed from an atom.
Penetration of orbitals
It is the ability of an orbital to attract an electron. This process is achieved together with release of energy. The high extent of penetration is a feature of orbitals. The penetration effect of S orbital is the maximum because of the closeness to the nucleus that are the p, d and f orbitals. It describes the proximity to which an electron can approach to the nucleus. In a multi electron system electron penetration is defined by an electron’s relative electron density near the nucleus of an atom. Electrons in different orbitals have different electron densities around the nucleus.
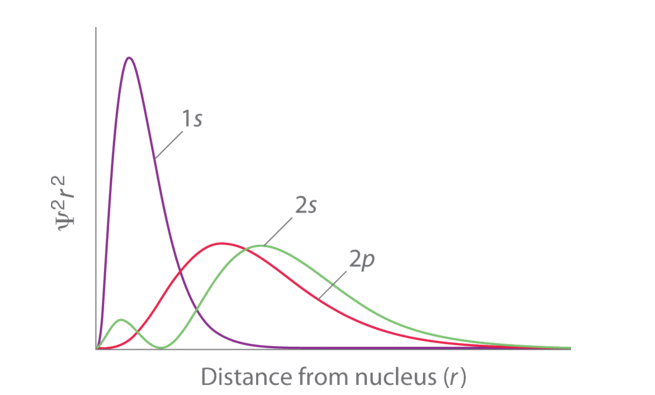
Fig. 1: Orbital Penetration.
The figure shows a distribution of radial probability of the 2p and 2s orbitals for various states of the hydrogen atom shows that the 2s orbital penetrates more inside the 1s orbital more than the 2p orbital. Subsequently, when an electron is in the small inner lobe of the 2s orbital, it experiences a comparatively large value of Zeff, which causes the energy of the 2s orbital to be lower than the energy of the 2p orbital.
Variation of s, p, d and f orbitals energies of atoms in the Periodic Table
Orbitals are regions of space where electrons are most likely to be found in an atom. These orbitals are designed as s, p, d, f among others. The energy increases as you move up the orbital in such a way that S orbital has the lowest energy and f orbital has highest energy as the energy levels increases the electrons are located further away from the nucleus.
S-orbitals
An S orbital is spherical symmetrical around the nucleus of an atom like a hollow ball with nucleus at the centre. As the levels of energy increase, the electrons are located further away from the nucleus, so the orbitals get bigger the order of size is
1s<2s<3s< ------ as shown
Fig.2: The figure shows that as the energy levels increase, the electrons move further away from the nucleus, as a result the orbitals get bigger in size the order of size is 1s<2s<3s<…
p orbitals
Unlike s orbitals, a p orbital points in a particular direction, at any one energy level we have three absolutely equivalent p orbitals pointing mutually at right angles to each other they are given symbols px, py, pz. The p-orbitals at the second energy level are called 2px, 2py,2pz and so on. All levels except the first energy level have p orbitals.
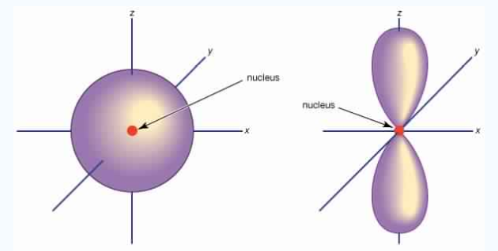
Fig.3: At any one energy level, we have absolutely three equivalent p orbital pointing
mutually at right angles to each other, They are arbitrarily given the symbols px, py, pz.
At any one energy, we have three absolutely equivalent p orbitals pointing mutually at right angles to each other. These are arbitrarily given the symbols px, py, pz, which is for convenience. the p orbitals at the second energy level are called 2px,2py,2pz. there are similar orbitals at subsequent levels: 3px,3py,3pz….and 4px, p4py,4pz and so on. All levels except the first have p orbitals.

Fig.4: In addition to s and p orbitals, there are two other sets of orbitals which become available for electrons to inhabit at higher energy levels, at the third level, there are a aet of five d orbitals as well as 3s and 3p orbitals, at the third level there are a total of nine orbitals.
d orbital
In addition to s and p orbitals, there are 2 other sets of orbitals which are available for electrons to inhabit at higher energy levels as well as the 3s and 3p orbitals at the third level there are now a total of nine orbitals altogether.
3dxy, 3dxz, 3dyz, 3dx2-y2, 3dz2

Fig. 5: The first group contains 3dxy,3dxz and3dyz orbitals, the names specify that these orbitals Lie in the x-y plane, the x-z plane and the y-z plane. Each lobe has four lobes and each lobe points between. Two axes and not along them. The second group contains the 3dx2-y2and3dz2 orbitals, these lobes point along various axes the 3dx2-y2 looks exactly like the first group, except that the lobes are pointing along. The x and y axes, not between them. The3dz2 looks like a p orbital...:
f orbital
At the fourth and higher levels there are 7f orbitals in addition to the 4s, 4p and 4d orbitals. Counting the 4s, 4p and 4d orbitals. This makes a total of 16 orbitals in the 4th level.
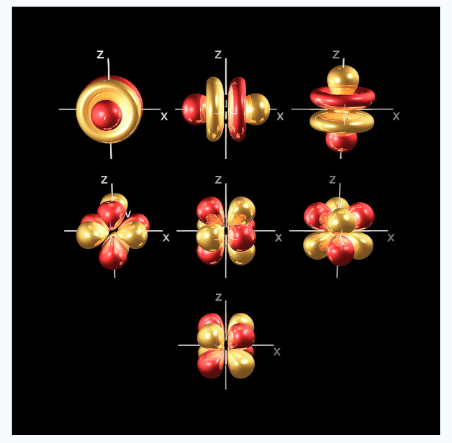
Fig.6: counting the 4s,4p,4d orbitals, this makes a total of 16 orbitals in the fourth level. The s, p, d and f orbitals are more complicated at higher energy levels.
Electron Configuration
Electron configuration holds the key to the chemical world. Our generation understands the chemical properties of organic and inorganic compounds based on the electronic configuration of the constituent elements.
Therefore, in a reaction the chemical bonding is the arrangement of electrons of reactant atoms. Classification of periodic table is based on the electron configuration of the elements.
The 3S orbital has lower energy than 3P orbitals which again has a lower energy than 3d orbitals. But the orbitals belonging to a particular type (P or d or f) will have an energy equal of an atom or an ion.
Rules for writing electronic configuration
The electron configuration of elements or its ions should be according to the following rules
Where l = 0, 1, 2, 3 for s, p, d, f orbitals respectively.
Electron configuration and energy levels
An easy way to remember these energy levels is provided below this diagram

Fig.7: The figure shows an increase in energy every orbital. S orbital have the lowest energy, energy continuously increases in each block as we move, downward in group of left to right across the period.
Electron shells
According to this diagram, the energy levels are
1S < 2S < 2P < 3S < 3P < 4S < 3d < 4P < 5S < 4d < 5P < 6S < 4f < 5d < 6P < 7S < 5f…
Pauli exclusion principle
Pauli exclusion principle uses for the pictorial representation of electron configuration.
No two electrons of the atom can have similar four quantum numbers.
An alternative statement of Pauli’s exclusion principle, not more than two electrons can be placed in only one and same orbital.
When an orbital contains two electrons, the electrons are paired. These two electrons per orbital given the maximum place for electrons.
Periodic table and electronic configuration
Extranuclear electrons are responsible for the chemical action of elements and periodic classification of the elements are also based on the chemical behavior.
Thus, the electronic configuration of elements must be related with the periodic table. Especially, the arrangement of the electrons in the outermost orbitals detects the position of the elements in the periodic table.
Atomic radii or size can be defined in the most simplified manner as the radii (or half the "width") of the spherical atoms. Nonbonding atoms have a much larger, more indefinite or "fuzzy" radius, therefore when atomic radius is described as a periodic trend, the thing that comes to mind is bonding atomic radius.
These are the radii of atoms that are chemically bonded to each another. So, if the bond between two Cl atoms in Cl2 is 1.99 angstroms, resulting in chlorine's bonding atomic radius as about 0.99 angstrom. These values are then used to estimate bond lengths between different elements in molecules.
Atomic radius generally increases from top to bottom down a group. This generally occurs due to the increase in the principal quantum number, (n). Therefore, when we go further down a column, the outer electrons move much further away from the atom, making the atom thus larger.
Generally, the atomic radius decreases as we move from left to right across a period. This occurs mainly due to effective nuclear charge. The greater the effective nuclear charge, the more will be the attraction felt by the outer electrons from the nucleus, and the closer the outer electrons are to the nucleus, making the atom smaller.
Ionic Size
Ionic radii are the radii of ions of elements. These distances are based on distances that exist between ions in ionic compounds.
Cations, or positively charged ions, are smaller in size than their "parent" atoms. This is because cations are formed when the outermost orbitals become empty due to absence of electrons. This also decreases electron-electron repulsions. Therefore, the resulting ions are smaller as there are not as many orbitals that are occupied and the effective nuclear charge affecting the remaining electrons increases, pulling electrons in more closely.
Anions, or negatively charged ions, are larger in size than their "parent" atoms. This is because of the addition of electrons form these ions, increasing electron-electron repulsions, making the electrons spread out more effectively. Also, effective nuclear charge felt by the outermost electrons decreases. For ions that carry the same charge (i.e., from parent elements of the same group), size increases from top to bottom as we go down a group.
Ionization Energy
The ionization energy of a chemical category (i.e., an atom or molecule) is the energy required to remove electrons from gaseous ions or atoms. This property is also referred to as the ionization potential and is measured in volts. In chemistry, it often refers to one mole of a substance (molar ionization energy or enthalpy) and is reported in kJ/mol. In atomic physics, the ionization energy is typically measured in the unit electron volt (eV). Atoms or molecules which are larger have lower ionization energy, while smaller molecules or atoms tend to have higher ionization energies.
The ionization energy is not the same for electrons of different molecular or ionic orbitals.
More specifically, the nth ionization energy is the energy required to eliminate the nth electron after the first n-1 electrons are removed. It is perhaps a measure of the tendency of an ion or atom to surrender an electron or the strength of the electron binding. The greater the ionization energy, the more difficult to remove an electron. The ionization energy may be an indicator to show the reaction of an element. Elements with a lower ionization energy tend to be reducing agents and form cations, and thereby combine with anions to form salts.
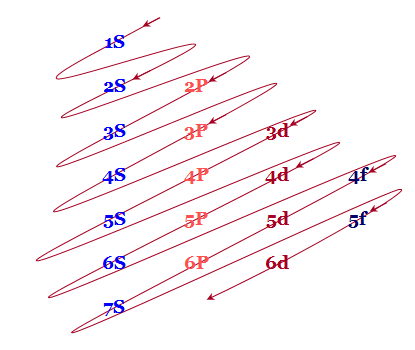
Fig.8: This graph shows the first ionization energy of the elements in electron volts(units).
Moving from left to right within a period or upward within a group, the first ionization energy shows an increase. As the atomic radius of an ion or atom reduces, it becomes difficult to remove an electron that is close to a more positively charged nucleus. On the other hand, as one moves down a group on the periodic table, the ionization energy will likely decrease since the valence electrons are far away from the nucleus and experience greater shielding. They experience a weaker attraction to the positive charge of the nucleus. Ionization energy increases when viewed from left to right in a specific time and decreases from top to bottom in a group.
Rationale for the Periodic Trends in Ionization Energy
The ionization energy of an element shows an increase as one move across the periodic table because the electrons are held together tightly by the highly effective nuclear charge. This is due to the additional electrons in the same shell do not substantially contribute to shielding each other from the nucleus, however an increase in atomic number corresponds to an increase in the number of protons in the nucleus.
The ionization energy of the elements shows an increase as one moves up a given group because the electrons are held in lower-energy orbitals, closer to the nucleus and thus more tightly bound (which is difficult to remove). The easiest element to ionize is francium and the hardest to ionize is helium respectively. Cesium is said to have the lowest ionization energy and Fluorine is said to have the highest ionization energy (with the exception of Helium and Neon).
Electron affinity reflects the ability of an atom to accept an electron. It is the energy change which occurs when an electron is added to a gaseous atom. Atoms with strong effective nuclear charge have greater electron affinity.
The reaction that occurs when an atom takes an electron may be represented as:
X + e− → X− + energy
Another way to define electron affinity is as the amount of energy needed to remove an electron from a singly charged negative ion:
X− → X + e−
Key Takeaways:
Electron Affinity Definition and Trend
Electron Affinity Trend
Electronegativity
Electronegativity is the property of an atom which increases with its tendency to attract the electrons of a bond. when two bonded atoms that have similar electronegativity values as each other, they share electrons equally in a covalent bond. Usually, the electrons present in a chemical bond are more attracted to one atom (the more electronegative one) than to the other one. This results in a polar covalent bond. If the electronegativity values are very different, the electrons do not show any sharing. One atom essentially takes the bond electrons from the other atom, forming an ionic bond.
Electronegativity is a property of an atom present within a molecule, rather than a fundamental property of an atom by itself. Thus, electronegativity varies depending on an atom's environment or surroundings. However, most of the time an atom displays similar behaviour in different situations. Factors that affect electronegativity include the nuclear charge and the position and number of electrons in an atom.
Electronegativity Example
The chlorine atom has a higher electronegativity than the hydrogen atom, so the bonding electrons will be closer to the Cl than to the H in HCl molecule.
In the O2 molecule, both atoms have the same electronegativity. The electrons in the covalent bond are shared equally between the two oxygen atoms.
Polarizability
The polarizability of a molecule is a measure of the ability of the molecule to respond to an electric field and obtain an electric dipole moment p. There are many microscopic mechanisms of polarization in a dielectric material. The Electric dipole moments may be permanent or may be induced by an electric field.
The induced electric dipole moment can be achieved as a result of two polarization phenomena, i.e., electronic polarization and distortion polarization.
Electronic polarization, αe, describes the shift of the cloud of bound electrons with reference to the nucleus under an applied electric field. The atom scatter, and the center of the atom’s negative charge eventually does not coincide with the position of the nucleus, resulting in an electric dipole moment. The electric dipole moment of each atom is described by
p=αeE*
Distortion polarization αd (also often referred to as ionic polarization) relates to the distortion of the position of the nuclei by the applied field, resulting in stretching or compressing the bond length, depending on the relative orientation between the electric field and ionic bond. The molecule is stretched and bent by the applied field and accordingly changes its dipole moment. Nonpolar molecules may acquire an induced dipole moment in an electric field as a result due to the distortion of the electric field that causes disturbance in electronic distributions and nuclear positions. A polar molecule is one with a permanent electric dipole moment. The permanent dipole moment is formed due to the partial charges on the atoms in the molecule that emerge from the different electronegativity or other features of bonding. Polar molecules may possess their existing dipole moments modified by the applied field. Orientation polarization identifies with the phenomenon of a permanent dipole moment as a result of polar molecules. The total polarization of a medium, composed of polarizable polar molecules, is therefore
P=N(αe+αd+μ23kT) E*
where N is the number of molecules per m3, μ is the orientation polarizability, k is the Boltzmann constant, and T is the temperature in K.
The terms αe and αd represent the electronic and distortion polarization in the molecule, while the term μ2/3kT stems from the thermal averaging of permanent electric dipole moments in the presence of an applied field. The quantitative relation between the relative permittivity and properties of the molecules is described by the Debye equation:
εr−1εr+2=N3ϵ0(αe+αd+μ23kT)
The relative permittivity εr of materials is high if its molecules are polar and highly polarizable. This equation shows that the permittivity is smaller if materials do not contain polar molecules. The reduction of density polarizabilities αe and αd and N are also possible ways of decreasing the dielectric constant. Reducing the number of ionic bonds in the material minimizes distortion polarization. The electronic polarization is minimized by lowering the electron density in the material, i.e., introducing smaller elements. The same expression, but without the permanent dipole moment contribution, is called the Clausius–Mossotti equation:
εr−1εr+2=N3ε0(αe+αd)
Although the value of the electric dipole moments is extremely important for predicting properties of dielectric materials, their calculation becomes difficult. In the case of simple molecules, the Stark effect is used to measure the electric dipole moment of molecules for which rotational spectra can be observed. In the case of more complicated cases, the permanent dipole moment and polarizability of molecules can be calculated by measuring εr at a series of temperatures. These measurements make it easy to determine the molar polarizations and their slope and intersect versus 1/T give values of dipole moment and polarizability.
Acids and Bases
For thousands of years people have known that vinegar, lemon juice, and many other foods taste sour. eventually, it was not until a few hundred years back that it was discovered why these foods taste sour – because they are all acids. The term acid, in fact, comes from the Latin term acere, which means "sour". While there may be different definitions of acids and bases, In the seventeenth century, An Irish writer and amateur chemist Robert Boyle first labelled substances as either acids or bases (he called bases alkalies), according to the following characteristics:
Acids: Acids become less acidic when mixed with bases they taste sour, are corrosive to metals, change litmus (a dye extracted from lichens) to red.
Bases: feel slippery, change litmus blue, and become less basic when mixed with acids.
While Boyle and others failed to explain why acids and bases behave the way they do, the first reliable definition of acids and bases was not be proposed until 200 years later.
In the late 1800s, the Swedish scientist Svante Arrhenius suggested that water can dissolve many compounds by separating them into their individual ions. Arrhenius suggested that acids are compounds that contain hydrogen and can dissolve in water to release hydrogen ions into a solution. For example, hydrochloric acid (HCl) dissolves in water as follows:
HCl H2O→ H+(aq) + Cl-(aq)
Arrhenius defined bases as those substances that can dissolve in water to release hydroxide ions (OH-) into the solution. For example, a typical base, sodium hydroxide (NaOH) was suggested by Arrhenius:
NaOH H2O→ Na+(aq) + OH-(aq)
The Arrhenius definition of acids and bases explains many things about Acids and Bases. Arrhenius's theory corelates how all acids have similar properties to each other (and, conversely, why all bases are similar): since all acids release H+ into solution (and all bases release OH-). The Arrhenius definition clearly explains Boyle's observation that bases and acids counteract each other. This idea, that a base can make an acid weaker, and that an acid can make a base weaker, is called neutralization.
Neutralization
As you can see from the equations, acids release H+ into solution and bases release OH-. If we were to mix an acid and base together, the H+ ion would combine with the OH- ion to make the molecule H2O, or plain water:
H+(aq) + OH-(aq) → H2O
The neutralization reaction of an acid with a base will always form water and a salt, as shown below:
Acid Base Water Salt
HCl + NaOH → H2O + NaCl
HBr + KOH → H2O + KBr
Though Arrhenius helped explain the fundamentals of acid/base chemistry, unfortunately his theories have limits. For example, the Arrhenius definition does not explain why some substances, such as common baking soda (NaHCO3), this compound act like a base even though they do not contain hydroxide ions.
In 1923, the Danish scientist Johannes Brønsted and the Englishman Thomas Lowry published an independent but similar paper that was defined in Arrhenius' theory. According to Bronsted’s, "... acids and bases are substances that are capable of releasing or taking up hydrogen ions, respectively." The Brønsted-Lowry definition has a widespread concept of the Arrhenius of acids and bases.
The Brønsted-Lowry definition of acids and bases is very similar to the Arrhenius definition: Any substance that can release a hydrogen ion is an acid. (According to the Brønsted definition, acids are seldom mentioned to as proton donors because an H+ ion, hydrogen minus its electron, is simply a proton).
The Brønsted definition of bases is, however, very different from the Arrhenius definition. The Bronsted theory of base is defined as any substance that can concede a hydrogen ion. In other words, a base is the opposite of an acid. NaOH and KOH, as seen above, would still be considered bases because they can accept an H+ from an acid to form water. However, the Brønsted-Lowry definition also explains the reasons why substances that do not contain OH- can still act like bases. Baking soda (NaHCO3), for example, acts like a base by accepting a hydrogen ion from an acid as illustrated below:
Acid Base Salt
HCl + NaHCO3 → H2CO3 + NaCl
In this example, the carbonic acid formed (H2CO3) undergoes rapid decomposition to water and gaseous carbon dioxide, and so the solution bubbles as CO2 gas are released.
pH
Under the Brønsted-Lowry definition, both acids and bases are related to the concentration of hydrogen ions present in the solution. Acids increase the concentration of hydrogen ions, while bases decrease the concentration of hydrogen ions (by accepting them). The acidity or basicity of a solution can be measured by its hydrogen ion concentration.
In 1909, the Danish biochemist Sören Sörensen invented the pH scale for measuring acidity. The pH scale is described by the formula:
pH = -log [H+]
For example, a solution with [H+] = 1 x 10-7 moles/liter has a pH equal to 7 (a simple way to think about pH is that it equals the exponent on the H+ concentration, without the minus sign). The pH scale has a range from 0 to 14. Substances that show a pH between 0 and less than 7 are acidic in nature (pH and [H+] are inversely related - lower pH means higher [H+]). Substances with a pH greater than 7 and up to 14 are basic in nature (higher pH means lower [H+]). Substances with a pH= 7, are neutral substances, for example, pure water.
Principle of HSAB theory
Ralph Pearson introduced the Hard Soft [Lewis] Acid Base (HSAB) principle in the early 1960s and made an attempt to unite inorganic and organic reaction chemistry. The impact of the new concept was immediate, however with the HSAB principle had rather fallen apart while other principles were introduced around the same time, such as frontier molecular orbital (FMO) theory and molecular mechanics, have flourished.
The Irving-Williams stability series (1953) had shown that for a given ligand the stability of dipositive metal ion complexes increases:

It was also found that a few ligands formed their most stable complexes with metal ions like Ti4, Al3+, and Co3+ while others were found to former stable complexes with Hg2+, Ag+ and Pt2+. In 1958 Ahrland et al. he had classified metal cations as Type A and Type B, where:
Type A metal cations included: Alkali metal cations: Li+ to Cs+, Alkaline earth metal cations: Be2+ to Ba2+, Lighter transition metal cations in higher oxidation states: Ti4+, Cr3+, Fe3+, Co3+ • The proton, H+
Type B metal cations include: • Heavier transition metal cations in lower oxidation states: Cu+, Ag+, Cd2+, Hg+, Ni2+, Pd2+, Pt2+. Ligands were classified as Type A or Type B depending upon whether they formed more stable complexes with Type A or Type B metals:
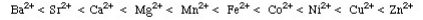
Fig.9: From this analysis, a principle was derived: Type A metals prefer to bind to Type A ligands and Type B metals prefer to bind to Type B ligands These empirical (experimentally derived) rules tell us that Type A metals are more likely to form oxides, nitrides, carbonates and fluorides, while Type B metals are more likely to form phosphides, selinides and sulphides. This pattern of analysis is importance economically because some metals are found in nature as sulfide ores: PbS, CdS, NiS, etc., while other are found in nature as carbonates: MgCO3 and CaCO3 and others as oxides: Fe2O3 and TiO2. This approach has been very successfully developed in last few years by Bruce Railsback. The Railsback analysis uses contours of behaviour overlapping upon the Mendeleev periodic table. Hard Soft [Lewis] Acid Base Principle In the early 1960s, Ralph Pearson developed the Type A and Type B logic by explaining in detail that the differential complex behaviour of cations and ligands in terms of electron pair donating Lewis bases and electron pair accepting Lewis’s acids: Lewis’s acid + Lewis base Lewis acid/base complex Pearson classified Lewis acids and Lewis bases as hard, borderline or soft.
Oxidation states
Oxidation state simplifies the whole process of working on what is being oxidised and being reduced in redox reactions. However, before the introduction, few things need to be known:
Let’s look at some examples from vanadium chemistry.
Vanadium forms a number of different ions - for example, V2+ and V3+. A doubt as to hoe these might be produced from vanadium metal, the 2+ ion will be formed as a result of oxidisation of the metal by removing two electrons:
The vanadium is now in an oxidation state of +2.
Further removal of another electron gives the V3+ ion:

The vanadium now has an oxidation state of +3.
Subsequently the removal of another electron gives a more unusual form of ion, VO2+.

The vanadium at present is in an oxidation state of +4. Therefore, the oxidation state is not counting the charge on the ion (which was true for the first two cases but not for this particular one).
The positive oxidation state is counting the total number of electrons which should have been removed - starting from the element.
In the next step it is also possible to remove a fifth electron to give another ion (this may be confused with the one before!). The oxidation state of the vanadium is now +5.

Every time you oxidise the vanadium by removing another electron from it, its oxidation state increases by 1.
If eventually electrons are added again the oxidation state will fall. And finally get back to the element vanadium where the oxidation state of zero.
What would be the case if we kept on adding electrons to the element? This cannot be done with vanadium, on the other hand with an element like sulphur.

According to this equation the sulphur compound has an oxidation state of -2.
Summary
Oxidation state shows the total number of electrons which have been added from an element (a negative oxidation state) or removed to an element (a positive oxidation state) to get to its present state.
Oxidation involves an increase in oxidation state
Reduction involves a decrease in oxidation state
This is a simple pattern and is the single most important thing about the concept of oxidation states. If the oxidation state of an element changes is known during a reaction, instantly it can be predicted whether it is being oxidised or reduced without having to work in terms of electron-half-equations and electron transfers.
Working out oxidation states
Oxidation states is not calculated by counting the numbers of electrons transferred. It would be a very long process. Instead, a few simple rules can be followed, and do some very simple sums!
Group 2 metals | always +2 |
|
Oxygen | usually -2 | except in peroxides and F2O (see below) |
Hydrogen | usually +1 | except in metal hydrides where it is -1 (see below) |
Fluorine | always -1 |
|
Chlorine | usually -1 | except in compounds with O or F (see below) |
Hybridization and Molecular Geometries
- A hybrid orbital or a mix of atomic orbitals
- An atomic orbital can interact with other atoms and overlap resulting in a given hybrid atomic orbital.
For example- here the sp hybrid atomic orbital is formed:

Fig.10: In picture, an atomic orbital can interact with other atoms and overlap resulting in a hybrid atomic orbital. The picture shows a sp hybrid orbital formed.
Molecular Orbitals
- single bonds are sigma bonds
- double and triple bonds each have one sigma bond
- double bonds have one pi bond
- triple bonds have two pi bonds
- there must be a sigma bond in order for a pi bond to occur
- Molecular Orbitals
Geometry
Bond | Hybridization | Geometry | Bond angle | Picture |
Single | sp3 | Tetrahedral | 109.5° |  |
Double | sp2 | Trigonal planar | 120° | 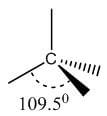 |
Triple | sp | Linear | 180° |
|
Bond | Hybridization | Geometry | Bond angle | Picture |
Single | sp3 | Tetrahedral | 109.5° |  |
Double | sp2 | Trigonal planar | 120° |  |
Triple | Sp | Linear | 180° | 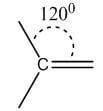 |
References:
1.The elements book – A visual encyclopaedia of the periodic table - Smithsonian
2. Essential textbooks in chemistry – Orbitals with application in Atomic Spectra – Charles. S. Mc Caw,
3. Atoms, electrons and change by Peter Atkins.