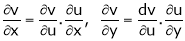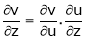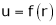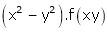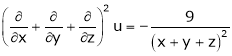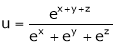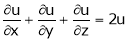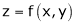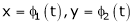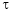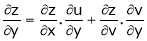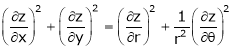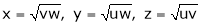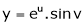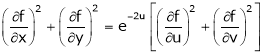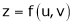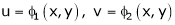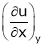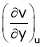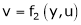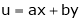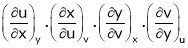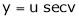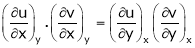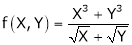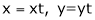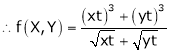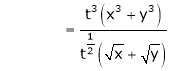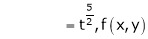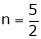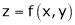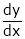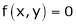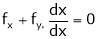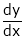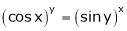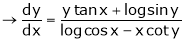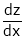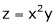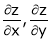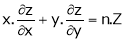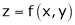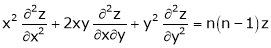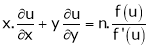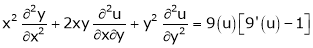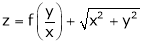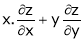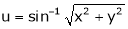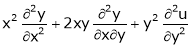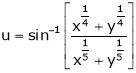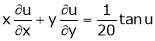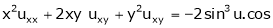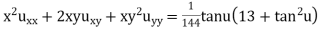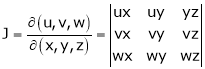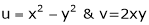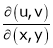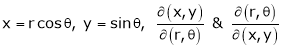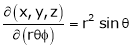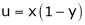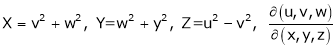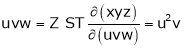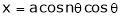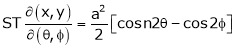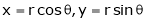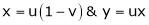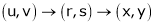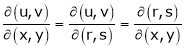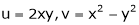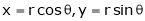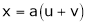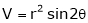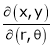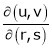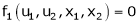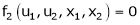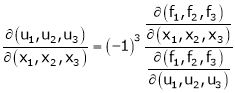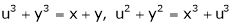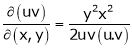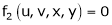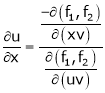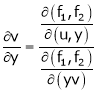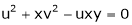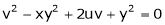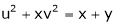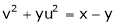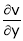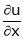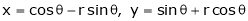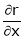Unit –3
Partial Differentiation
Partial Differentiation
If 
Prove that 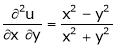
Partial differentiation of function of function
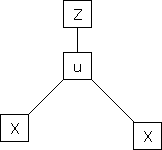
If z = f(u) and  . Then z becomes a function of x & y. In this case z becomes a function of function of x & y.
. Then z becomes a function of x & y. In this case z becomes a function of function of x & y.
i.e.
|
Then
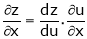 ,
,



Similarly
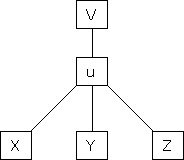
If 
Then z becomes a function of function of x, y & z.
Prove that
2. If V =
3. If
4. If
|
Partial Differentiation of composite function
a) Let i.e.
b) Let i.e.
& Continuing in this way, ….. Ex. If
Ex. If
Where
Ex. If
i) ii)
|
Notations of partial derivatives of variable to be treated as a constant
Let
i.e.
Then To find i.e. To find
Ex. If
Ex. If
|
A polynomial in x & y is said to be Homogeneous expression in x & y of degree n. if the degree of each term in the expression is same & equal to n.
e.g.
 is a homogeneous function of degree 3.
is a homogeneous function of degree 3.
To find the degree of homogeneous expression f(x, y).
- Consider
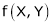
- Put
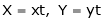 . Then if we get
. Then if we get  .
.
Then the degree of  is n.
is n.
Ex.

Consider |
Put |
|
|
|
|
Thus degree of f(x, y) is |
Note that |
If |
|
Differentiation of Implicit function
Suppose that we cannot find y explicitly as a function of x. but only implicitly through the relation f(x, y) = 0. Then we find Since
i.e. Similarly, it f (x, y, z) = 0 then z is called implicit function of x, y. then in this case we get
Ex. Find
Ex. Find Ex. If Find
Ex. If Then find Eulers Theorem on Homogeneous functions: Statement: If
Deductions from Eulers theorem
2. If
And
Where
Ex. If
Ex. If
Ex. If That
Ex. If
Ex. If That
|
Jacobians, Errors and Approximations, maxima and minima
Jacobians If u and v be continuous and differentiable functions of two other independent variables x and y such as
Similarly , JJ’ = 1
Actually Jacobins are functional determines Ex.
ST 4. 5. If 6. 7. If 8. If JJ1 = 1 If
JJ1=1 Jacobian of composite function (chain rule)
Then Ex.
Where
2. If
Find 3. If
Find
|
Jacobian of Implicit function
Let u1, u2 be implicit functions of x1, x2 connected by f1, f2 such there |
|
Then |
Similarly, |
|
Ex. If
If Find
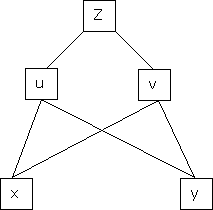
Partial derivative of implicit functions Consider four variables u, v, x, y related by implicit function.
Then
Ex. If Find If Find
Find
If Find
|
Reference Books:
1. Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.)
2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education)
3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning)
4. Thomas’ Calculus by George B. Thomas, (Addison-Wesley, Pearson)
5. Applied Mathematics (Vol. I & Vol. II) by P.N.Wartikar and J.N.Wartikar Vidyarthi Griha Prakashan, Pune.
6. Linear Algebra –An Introduction, Ron Larson, David C. Falvo (Cenage Learning, Indian edition)