Unit - 5
Elementary theory about dependence analysis
When terms like dependence analysis and automatic parallelization are discussed, images of loop programs and array variables come to mind. This is unsurprising, given that loops are the most common repeating structure in any programming language, and loops are clearly where programs spend the most of their time. Second, there has been a long research effort on parallelizing large numerical applications (e.g., FORTRAN programs) on supercomputers because of the early focus on high performance computing for large numerical applications (e.g., FORTRAN programs). The field has been active for more than a quarter-century, and there are a number of well-known texts on the subject.
Any approach to automatic parallelization must be based on the following fundamental notions: I detecting which statements in which iterations of a (possibly multiply nested and possibly imperfect) loop are dependent on each other, in the precise sense that one produces a value that is consumed by the other; (ii) determining which operations can be executed in parallel; and (iii) transforming the program so that this choice of parallelization is rendered explicit The first issue is known as dependency analysis, the second as the additional study required to select the parallelization, and the third as program or restructure.
These are exceedingly challenging problems in general. Nonetheless, there are elegant and powerful solutions accessible for some classes of programs. Rather than providing "yet another review" of a broad area, we present a less well-known technique termed the polyhedral model. The model is based on a mathematical model of both the parallelized program and the tools used for analysis and transformation. Operational research, linear and nonlinear programming, and functional and equational programming are all used. Its application, on the other hand, is limited to a well-defined (but nonetheless significant) subset of imperative programs.
Types of dependence
Data dependences (also known as genuine data dependences), name dependences, and control dependences are the three categories of dependencies.
Data dependence
If either of the following conditions occurs, an instruction j is data dependent on instruction I
● Instruction j is data dependent on instruction k, and instruction k is data dependent on instruction I or
● Instruction j produces a result that can be used by instruction j, or
The second condition simply asserts that one instruction is dependent on another if the two instructions have a chain of first-type dependencies. This chain of dependencies can be as long as the application itself.
Consider the following code sequence, which uses a scalar in register F2 to increment a vector of values in memory (beginning at 0(R1) and ending at 8(R2)):
Loop: L.D F0,0(R1); F0=array element ADD.D F4, F0, F2; add scalar in F2 S.D F4,0(R1); store result DADDUI R1, R1, #-8; decrement pointer 8 bytes (/e BNE R1, R2, LOOP; branch R1! =zero
The reliance means that between the two instructions there would be a chain of one or more data dangers. When multiple instructions are executed at the same time, a processor with pipeline interlocks detects a hazard and stalls, decreasing or eliminating the overlap. Programs have dependencies as a property.
The pipeline organization determines if a given dependency results in an actual danger being discovered and whether that hazard causes a stall. This distinction is crucial to grasping how instruction-level parallelism might be utilized.
The presence of a dependency signals the possibility of a hazard, but the actual hazard and length of any stall are pipeline properties. The significance of data dependencies is that they are dependent.
(1) Denotes the presence of a hazard,
(2) Establishes the order in which calculations must be performed, and
(3) Defines the maximum amount of parallelism that can be used.
Name dependence
When two instructions use the same register or memory location, termed a name, but there is no data transfer between the instructions associated with that name, this is known as name dependence.
There are two different forms of name dependencies between instructions I and j in program order:
● When instruction j writes a register or memory address that instruction I reads, there is an anti-dependency between the two instructions. To guarantee that I read the proper value, the original ordering must be kept.
● When instruction I and instruction j both write to the same register or memory location, this is known as output dependency. To ensure that the value finally written corresponds to instruction j, the ordering between the instructions must be preserved.
Because no value is communicated between the instructions, both anti-dependences and output dependences are name dependences rather than real data dependences. Because a name dependence is not a genuine dependency, instructions in a name dependence can run at the same time or be reordered if the name (register number or memory address) used in the instructions is modified to avoid conflict.
Control dependence
A control dependence establishes how an instruction, I is ordered in relation to a branch instruction so that it is executed in the correct program sequence. Except for those in the first basic block of the program, every instruction is control dependent on a set of branches, and these control dependencies must be preserved in order to maintain program order. The dependency of the statements in the "then" part of an if statement on the branch is one of the simplest examples of a control reliance. In the code section, for example:
If p1 { S1;
};
If p2 { S2;
}
S1 is controlled by p1, while S2 is controlled by p2 but not by p1. Control dependencies impose two types of constraints in general:
1. An instruction that is control dependent on a branch cannot be shifted before the branch so that it no longer has control over its execution. We can't, for example, relocate an instruction from the then-part of an if-statement before the if-statement.
2. An instruction that is not control dependent on a branch cannot be put after the branch to allow the branch to control its execution. We can't, for example, shift a sentence preceding the if-statement inside the then-portion.
Two aspects of a basic pipeline preserve control dependence: first, instructions execute in program order. This sequence ensures that any instructions that come before a branch are executed first. Second, control or branch dangers are detected, ensuring that an instruction that is control reliant on a branch is not performed until the branch direction is known.
Key takeaway
When terms like dependence analysis and automatic parallelization are discussed, images of loop programs and array variables come to mind.
This is unsurprising, given that loops are the most common repeating structure in any programming language, and loops are clearly where programs spend the most of their time.
The following are two approaches for utilizing parallelism in parallel computer architecture:
Pipelining
Several functional units work in parallel to complete a single computation in pipelining. An assembly line or pipeline is made up of these functional units. Each functional unit specifies a phase of the calculation, and each computation passes through the pipeline.
If there is only one computation to run, the pipeline will not be able to extract any parallelism. When the same computation must be performed several times, the functional units can be used to overlap the computations.
Assume the pipeline has N functional units (stages) and the slowest requires T time to complete its function. Every Tth moment, a new computation can be initiated in this situation. When all of the functional units are working on a different computation, the pipeline fills up. Once the pipeline is full, every Tth instant a new computation is completed.
Systolic arrays provide an example of pipelining in action. However, in this case, the array's processor builds the pipeline in one or two dimensions. The wavefront array is an asynchronous variation of the systolic array, in which data is transported using the data flow principle while the systolic systems' pipeline mechanism is kept.
Replication
The replication of functional units such as a processor is a common approach of bringing parallelism to a computer. As long as there are replicated computing resources available, replicated functional units and data components can perform a same action concurrently. The array processor is a classic example, which consists of a large number of identical processors that perform the same function on many data components.
Along with pipelining parallelism, replication is used in wavefront arrays and two-dimensional systolic arrays. Replication is the primary parallel mechanism used by all MIMD designs. Both VLIW and superscalar processors can use it inside the processor. Some multi-threaded processors are built to take advantage of replication.
However, memory banks, as well as CPU units, can be copied. The method of interleaved memory design is well-known for reducing memory latency and improving execution.
I/O units, on the other hand, can be advantageously reproduced, resulting in increased I/O throughput. The simplest technique of replication is to increase the number of address and data lines in the processor bus. Microprocessor buses have progressed from 8-bit buses to 64-bit buses, and this trend is unlikely to slow down very soon.
Key takeaway
Several functional units work in parallel to complete a single computation in pipelining. An assembly line or pipeline is made up of these functional units.
The replication of functional units such as a processor is a common approach of bringing parallelism to a computer.
Branch prediction is a computer architecture strategy that aims to reduce the expenses of branching. Branch prediction uses pipelining to speed up the processing of branch instructions on CPUs. If particular predicates are true, the approach only executes certain instructions. A branch predictor is often used to implement branch prediction in hardware.
Prediction is another name for branch prediction, which is also known as branch predication.
Branch prediction is a technique for speeding up the execution of instructions on pipelined processors. CPUs used to execute instructions one by one as they came in, but with the introduction of pipelining, branching instructions may cause the processor to slow down dramatically because the conditional leap had to be processed first.
Branch prediction, like predicate logic, divides down instructions into predicates. If a predicate is true, a CPU utilizing branch prediction will only execute statements. Using conditional logic is one example. The processor can perform considerably more efficiently because no superfluous code is executed. Branch prediction is implemented in CPU logic with a branch predictor.
Branch prediction is an ancient technique for enhancing speed that is still relevant in current systems. While basic prediction approaches provide for quick look up and power efficiency, they have a high rate of misprediction.
Complex branch predictions, on the other hand, whether neural-based or versions of two-level branch prediction, improve prediction accuracy while consuming more power and increasing complexity exponentially.
Furthermore, the time it takes to anticipate the branches in complex prediction approaches is very long – ranging from 2 to 5 cycles – and is comparable to the time it takes to execute actual branches.
Branch prediction is fundamentally an optimization (minimization) problem in which the goal is to obtain the lowest possible miss rate, low power consumption, and low complexity while using the smallest amount of resources possible.
Categories
Branches can be divided into three categories:
Forward conditional branches - The PC (Program Counter) is altered to point to an address forward in the instruction stream based on a run-time situation.
Backward conditional branches - The PC's position in the instruction stream is reversed. The branch is based on a condition, such as branching backwards to the start of a program loop when a test at the end of the loop indicates that the loop should be run again.
Unconditional branches - Jumps, procedure calls, and returns with no explicit condition fall under this category. An unconditional jump instruction, for example, might be coded in assembly language as "jmp," and the instruction stream must be directed to the target location pointed to by the jump instruction right away, whereas a conditional jump, coded as "jmpne," would redirect the instruction stream only if the result of a previous "compare" instruction shows the values are not equal. (The x86 architecture's segmented addressing scheme adds to the complexity by allowing for "near" (inside a segment) or "far" (between segments) jumps) (outside the segment). Each type has different effects on branch prediction algorithms.)
Static branch prediction
Because it does not rely on information about the dynamic history of code execution, static prediction is the simplest branch prediction technique. Instead, it anticipates a branch's consequence simply based on the branch command.
Single-direction static branch prediction was utilized in the early implementations of SPARC and MIPS (two of the first commercial RISC architectures): they always predicted that a conditional jump would not be taken, therefore they always fetch the next sequential instruction. The instruction pointer is set to a non-sequential address only after the branch or jump is assessed and found to be taken.
Both CPUs have a one cycle instruction fetch and evaluate branches in the decode step. As a result, the branch target repeats every two cycles, and the machine fetches the instruction immediately after any taken branch. In order to use these fetched instructions, both architectures create branch delay slots.
A more advanced kind of static prediction assumes that backward branches will be followed but not forward branches. A backward branch has a target address that is lower than the branch's own. This technique can aid in the accurate prediction of loops, which are typically backward-pointing branches that are taken more frequently than not.
Dynamic branch prediction
Dynamic branch prediction predicts the outcome of a branch based on information acquired at runtime regarding taken or not taken branches.
Key takeaway
Branch prediction is a computer architecture strategy that aims to reduce the expenses of branching.
Branch prediction uses pipelining to speed up the processing of branch instructions on CPUs.
Branch prediction is a technique for speeding up the execution of instructions on pipelined processors.
The never-ending need to miniaturize everything is a major driving force in the microprocessor business. Smaller transistors consume less power and produce less heat because they require less voltage to operate. Faster clock speeds are also possible due to shorter connection distances. Most importantly, because more circuits may fit on a single wafer, reduced die areas result in cheaper CPUs. The 4004, which contained 2300 transistors, was Intel's first microprocessor. Chips today, on the other hand, have between 5 and 20 million transistors. What are they going to do with all of those transistors?
Caches, of course, take up a lot of space. Many wires must run to and from the read and write ports on caches and any IC (integrated circuit) based memory device. The load/store unit in the CPU must be able to access every position in the cache from both the read and write ports when using on-chip caches. When there are several load/store units, the problem becomes considerably worse. That's quite a few wires! A single package contains both the CPU chip and the L2 cache chip in the Pentium Pro; the CPU chip has roughly 5 million transistors, while the cache chip has about 15 million transistors.
Even when caches are taken into consideration, today's devices have a far higher number of transistors than the 4004. Microprocessors are, without a doubt, becoming more complicated. This growing complexity is understandable, as chip makers strive to produce fast processors that are also economical. As process technology advanced and more transistors could be packed into the same die area, it became more cost-effective to add new or better functionality to the processor in order to boost its effective speed. Dynamic scheduling is one of these enhancements.
In contrast to a statically scheduled system, where the compiler sets the order of execution, dynamic scheduling is a method in which the hardware determines which instructions to execute. In other words, the processor is processing instructions in a haphazard manner. Dynamic scheduling is similar to a data flow machine, in which instructions are executed based on the availability of the source operands rather than the order in which they appear. Naturally, a real processor must account for the restricted quantity of resources available. As a result, instructions are executed based on the availability of source operands as well as the requested functional units.
Parallelism that would not be visible at build time can be taken advantage of by dynamically scheduled machines. They're also more adaptable because the hardware handles much of the scheduling, so programs doesn't have to be recompiled to run effectively. To take advantage of the machine's specific hardware on a statically scheduled machine, code would have to be recompiled. (All of this is based on the assumption that both machines have the same instruction set architecture.) Of course, if the computers utilized different ISAs, the code would have to be recompiled regardless.)
The usage of in-order instruction issuing and execution is a key drawback of simple pipelining techniques: Instructions are issued in program sequence, and if one stalls in the pipeline, none of the others can advance. As a result, if two closely spaced instructions in the pipeline are dependent on each other, there will be a danger and a stall. If there are several working units, some of them may be idle. If instruction j is dependent on a long-running instruction I which is now operating in the pipeline, then all instructions after j must be blocked until I is completed and j may run.
Consider the following code:
DIV.D F0, F2, F4
ADD.D F10, F0, F8
SUB.D F12, F8, F14
WAR and WAW risks are introduced by out-of-order execution, which do not exist in the five-stage integer pipeline or its logical extension to an in-order floating-point pipeline.
In addition, out-of-order completion complicates the management of exceptions. Exception behavior must be preserved in dynamic scheduling with out-of-order completion, in the sense that only those exceptions that would occur if the program were executed in strict program order actually occur.
There are two reasons why imprecise exceptions can occur:
1. The pipeline may have completed instructions that are later in the program order than the exception-causing instruction, and
2. Some instructions earlier in the program order than the exception-causing instruction may not have been completed by the pipeline.
Dynamic Scheduling Using Tomasulo’s Approach
Robert Tomasulo designed this method, which was initially implemented in the IBM 360/91. It eliminates output and anti-dependencies, such as WAW and WAR risks, by renaming registers. There are no actual data dependencies in output and anti-dependencies; they are merely names.
Through the use of reservation stations, Tomasulo's technique achieves register renaming. Reservation stations are buffers that retrieve and store operands for instructions as soon as they become available.
Furthermore, awaiting instructions identify the reservation station that will offer input. Finally, when multiple writes to a register occur at the same time, only the last one is used to update the register. The register specifies for pending operands is renamed to the names of the reservation station when instructions are provided, which offers register renaming.
The floating-point unit and the load/store unit are both included in the basic construction of a Tomasulo-based MIPS processor.
The instruction unit sends instructions to the instruction queue, where they are issued in FIFO order.
The reserve stations include information for recognizing and resolving dangers, as well as the operation and real operands. Load buffers serve three purposes: they retain the components of the effective address until they are computed, they track outstanding loads waiting on memory, and they store the results of completed loads waiting for the CDB.
Store buffers, likewise, serve three purposes: they hold the components of the effective until they are computed, they hold the destination memory addresses of outstanding stores that are waiting for the data value to be stored, and they hold the address and value to store until the memory unit is available.
All data from the FP units and the load unit is recorded on the CDB, which is then sent to the FP register file, reservation stations, and storage buffers. The FP multipliers perform multiplication and division, while the FP adders perform addition and subtraction.
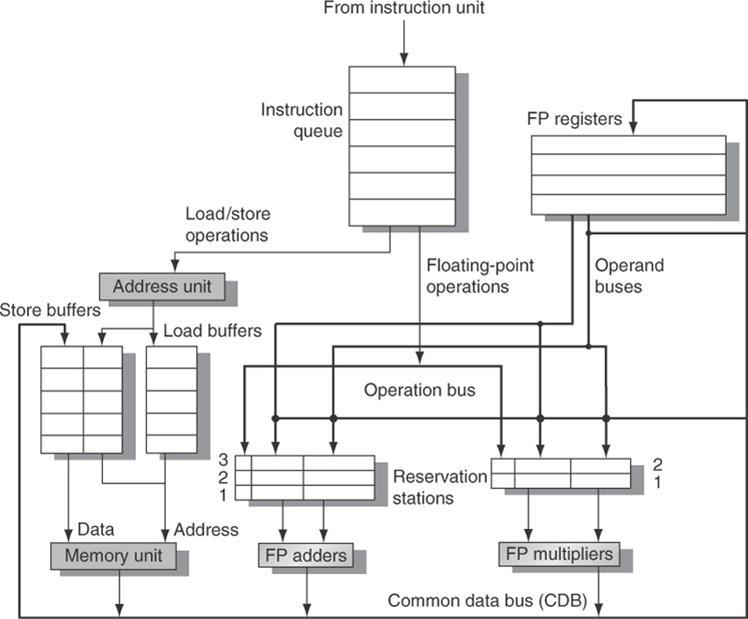
Fig 1: The basic structure of a MIPS floating point unit using Tomasulo’s algorithm
Tomasulo's approach consists of simply three steps:
- Issue - From the top of the instruction queue, get the next instruction. Issue the instruction to the station with the operand values if there is a matching reservation station that is empty (renames registers).
2. Execute (EX) - Place the operands in the respective reserve stations for execution once all of the operands are available. If operands aren't ready yet, keep an eye on the common data bus (CDB) as you wait for them to be computed.
3. Write result (WB) - When the result is ready, write it to the CDB, then to the registers and any reservation stations (including store buffers) that have been waiting for it. During this step, stores also write data to memory: once the address and data value are both available, they are transmitted to the memory unit, and the store completes.
Key takeaway
When dependencies are unknown at compile time, Dynamic Scheduling is utilized to address particular instances.
When the hardware rearranges the execution of instructions to reduce stalls while maintaining data flow and exception behavior, the stalls are reduced.
In a pipelined implementation, we can only expect a CPI of one. We should investigate the possibility of issuing and finishing numerous instructions every clock cycle if we want to cut CPI even more. For example, a CPI of 0.5 should be achieved if two instructions are issued and completed every clock cycle. Multiple issue processors are the name for such processors.
Superscalar processors and VLIW (Very Long Instruction Word) processors are the two main types of multiple issue processors. Superscalar processors come in two varieties, each with a different number of instructions per clock. They really are.
● Statically scheduled superscalar - In-order execution of statically scheduled super scalars.
● Dynamically scheduled superscalar - Out-of-order execution for dynamically scheduled super scalars.
VLIW processors
VLIW processors, on the other hand, send out a fixed number of instructions, either as a single huge instruction or as a fixed instruction packet, with the parallelism between instructions expressly stated in the instruction. EPIC–Explicitly Parallel Instruction Computers–is another name for them. The Intel/HP Itanium CPU is one example. The table below provides a summary of the various types' characteristics.
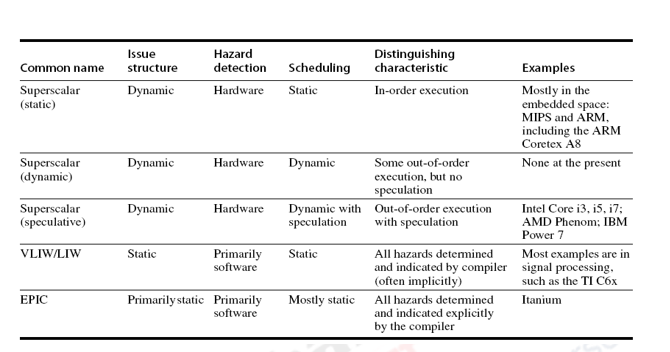
Superscalar processors decide how many instructions to send out on the fly. In-order processors are used when instructions are sent to the backend in program order. Static scheduling is used for in-order processors, which means that the scheduling is done at build time. Any dependencies between instructions in the issue packet and instructions currently in the pipeline must be checked by a statically scheduled superscalar.
Because the compiler conducts the majority of the effort of locating and scheduling instructions for parallel execution, they require extensive compiler aid to achieve good performance. A dynamically scheduled superscalar, on the other hand, requires less compiler aid but incurs large hardware expenditures. Out-of-order (OOO) processors are used when instructions can be sent to the backend in any sequence. The hardware dynamically schedules OOO processors.
Using compiler technology to minimize potential pauses due to hazards is an alternative to the superscalar technique. The instructions are formatted in a potential issue packet, which eliminates the requirement for the hardware to check for dependencies directly. The compiler either ensures that there are no dependencies in the issue packet or indicates when one exists. VLIW was the moniker given to this architectural technique.
We concentrate on a wider-issue processor since the advantage of a VLIW grows as the maximum issue rate grows. Indeed, the overhead of a superscalar is probably negligible for simple two-issue processors. We chose to focus our example on such architecture because VLIW methods make sense for bigger CPUs.
A VLIW processor, for example, might include instructions with five operations: one integer operation (which could alternatively be a branch), two floating-point operations, and two memory references, for example. Each functional unit would have its own set of fields, ranging from 16 to 24 bits per unit, for a total instruction length of 112 to 168 bits.
Statically scheduled superscalar processors
We issue instructions in issue packets with a number of instructions ranging from 0 to 8 in such processors. If we imagine a four-issue superscalar, the fetch unit will receive up to four instructions. All four instructions may or may not be available from the fetch unit. All dangers are checked in hardware during the issue stage (dynamic issue capability). The pipeline control logic must check for hazards between instructions in the issue packet as well as between instructions in the packet and those already in execution. Only the preceding instructions are issued if one of the instructions in the package cannot be issued.
Statically Scheduled Superscalar MIPS
Assume a superscalar MIPS that is statically scheduled and that two instructions are issued each clock cycle. The first is a floating-point operation, while the second is a Load/Store/Branch/Integer action. This is a lot easier and less demanding than dealing with a random dual issue.
Every clock cycle, up to two instructions must be fetched for this CPU. The hazard verification technique is quite simple, as the issue packet's restriction of one integer and one FP instruction reduces the majority of danger possibilities. When the integer instruction is a floating-point load, store, or move, the only issues arise.
This option causes congestion for the floating-point register ports, as well as a new RAW hazard if the second of the pair's instructions is dependent on the first. Finally, the selected instructions are dispatched to the appropriate functional units for execution.
Dynamically Scheduled Superscalar MIPS
Dynamic scheduling, like we described in previous modules with single issue processors, is one approach for enhancing performance in a multiple issue processor as well. Dynamic scheduling, when applied to a superscalar processor, not only enhances performance when data dependencies exist, but it also allows the processor to potentially transcend problem constraints. That is, even if the hardware can't start more than one integer and one FP operation in a clock cycle, dynamic scheduling can get around this limitation at the instruction level, at least until the hardware runs out of reservation stations.
Let's pretend we wish to add dual problem support to Tomasulo's algorithm. Reservation stations will need to receive instructions in order. Otherwise, the semantics of the program will be violated. We can assume that any combination of instructions can be issued, but this will make the instruction issue substantially more difficult.
Alternatively, the data structures for the integer and floating-point registers can be separated. Then, as long as the two issued instructions do not access the same register set, we can issue a floating-point instruction and an integer instruction to their respective reservation stations at the same time. Multiple instructions per clock in a dynamically scheduled processor have been issued using two separate ways. They are as follows:
● Two instructions can be processed in one clock cycle thanks to pipelining.
● Two instructions can be processed in one clock cycle thanks to pipelining.
● Increase the logic to handle two instructions, taking into account any possible dependencies. Both approaches are frequently used in modern superscalar processors that issue four or more instructions per clock — they both pipeline and broaden the issue logic.
Dynamically Scheduled Superscalar MIPS with Speculation
With conjecture, the performance of the dynamically planned superscalar can be increased even more. With regard to single issue processors, the concept of speculation has already been considered. Multiple issue processors are treated the same way. Beyond the branch, instructions are not only fetched and issued, but also carried out. The outcomes are recorded in the ROB. The results are written from the ROB to the register file or memory when the instruction is scheduled to commit. Figure shows the architecture of a dynamic scheduler with speculation support.

Fig 2: Architecture of a dynamic schedule
Issue, execute, write result, and commit are the four steps in the instructions. Figure shows the whole schedule for three iterations of the same loop.
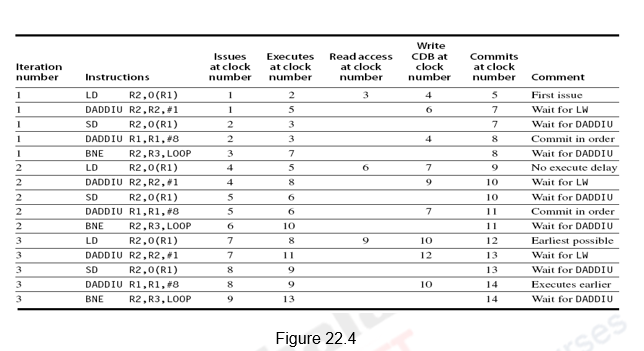
Fig 3: Whole schedule for three iterations
The schedule is generated in the same way as before, with the following modifications:
● A fourth stage called commit is included because it is a speculative execution.
● Furthermore, because this is a speculative execution, the instructions after the Branch do not need to wait for the branch to resolve.
● Despite the fact that the branch is only resolved in clock cycle 7, the following LD instruction is executed in clock cycle 5.
● Two CDBs and two commits per clock cycle have been assumed because multiple issue and execute could result in multiple instructions ending in the same clock cycle.
Design Issues with Speculation
There will be a lot of design concerns to think about. They'll be mentioned farther down.
● How Much Can We Speculate?
One of the key advantages of speculation is that it can manage events like cache misses that would otherwise delay the pipeline. The advantage of speculation is lost if the processor speculates and executes a costly event like a TLB miss, only to discover later that it should not have been executed. As a result, most pipelines using speculation will only handle low-cost exceptional events in speculative mode (such as a first-level cache loss). If a costly exceptional event occurs, such as a second-level cache miss or a TLB miss, the processor will not handle the event until the speculative instruction that caused it is no longer speculative. While this may somewhat reduce the performance of some programs, it prevents considerable performance losses in others, particularly those with a high frequency of such events and poor branch prediction.
● Speculating on Multiple Branches: We usually presume that we will only speculate on one branch. What happens if a new branch appears before the previous branch is resolved? Is it possible to speculate on numerous branches? This becomes more sophisticated and becomes a problem of design.
● Window Size: If the issue unit needs to look at n instructions (n is our window size) to discover the ones that can be issued at the same time, it will need to make (n-1)2 comparisons. A window with four instructions would necessitate nine comparisons, whereas a window with six instructions would necessitate twenty-five. These comparisons must be completed quickly so that instructions can be issued and data conveyed to reservation stations and ROB in the same cycle. In only one cycle, that's a lot of work! Modern processors have a window size of 2 to 8, with the most aggressive having a window size of 32.
Key takeaway
In a pipelined implementation, we can only expect a CPI of one. We should investigate the possibility of issuing and finishing numerous instructions every clock cycle if we want to cut CPI even more.
VLIW processors, on the other hand, send out a fixed number of instructions, either as a single huge instruction or as a fixed instruction packet, with the parallelism between instructions expressly stated in the instruction.
- The hardware model
All artificial limits on ILP are abolished in an ideal processor. In such a CPU, the only constraints on ILP are those imposed by actual data flows through registers or memory.
The following are the assumptions made for an ideal or perfect processor:
● Register renaming - Because there are an endless number of virtual registers available, all WAW and WAR dangers are avoided, and an unbounded number of instructions can start running at the same time.
● Branch prediction - The branch prediction is flawless. Every conditional branch is precisely predicted.
● Jump prediction - All jumps are perfectly predicted (including the jump register used for return and computed jumps). This is equal to having a processor with perfect speculation and an infinite buffer of instructions ready for execution when combined with perfect branch prediction.
● Memory address alias analysis - Because all memory addresses are known in advance, a load can be placed ahead of a store as long as the addresses are not identical.
2. Limitations on the Window Size and Maximum Issue Count
A dynamic processor may be able to match the level of parallelism revealed by our ideal processor more accurately.
Consider what the ideal processor should be capable of:
● Look arbitrarily far ahead to find a set of instructions to send out that exactly predicts all branches.
● To avoid WAR and WAW dangers, rename all registers.
● Determine whether any of the instructions in the issue packet have data dependencies; if so, rename accordingly.
● Determine whether the issuing instructions have any memory dependencies and how to manage them.
● Provide enough functional units that can be replicated to allow all of the ready instructions to be issued.
3. The Effects of Realistic Branch and Jump Prediction
Our ideal processor implies that branches can be perfectly predicted: before the first instruction is performed, the outcome of any branch in the program is known.
The five levels of branch prediction depicted in these diagrams are as follows:
● Perfect - At the start of the execution, all branches and leaps are properly predicted.
● Tournament-based branch predictor - A correlated two-bit predictor and a non-correlating two-bit predictor are used in the prediction scheme, together with a selector that chooses the best predictor for each branch.
● Standard two-bit predictor with 512 two-bit entries - To predict returns, we also assume a 16-entry buffer.
● Static - A static predictor looks into the program's profile history and forecasts whether a branch will always be taken or never be taken based on the profile.
● None - Although no branch prediction is utilized, jumps are predicted. Within a basic block, parallelism is generally limited.
4. Limitations on ILP for Realizable Processors
Processor performance at a high degree of hardware support, on par with or better than what is expected in the next five years. We assume the following fixed qualities in particular:
● There are no problem constraints on up to 64 instruction issues per clock. The practical ramifications of very broad issue widths on clock rate, logic complexity, and power may be the most significant barrier on using ILP, as we will explain later.
● A 1K-entry tournament predictor with a 16-entry return predictor. This predictor is on par with the top predictors from 2000, and it is not a main bottleneck.
● Perfect dynamic disambiguation of memory references—a lofty goal, but one that might be achievable with small window sizes (and hence small issue rates and load/store buffers) or a memory dependence predictor.
● Register renaming to add 64 more integer and 64 additional FP registers, surpassing the greatest amount available on any processor in 2001 (41 and 41 on the Alpha 21264), but likely within two or three years.
In some applications, ILP can be limiting or difficult to use. More importantly, it may result in an increase in energy usage. Furthermore, there may be significant parallelism occurring naturally at a higher level in the program that the methodologies used to exploit ILP cannot exploit. An online transaction processing system, for example, includes built-in parallelism among the various searches and updates that requests present. Because these inquiries and changes are essentially independent of one another, they can be processed in parallel. Because it is conceptually structured as independent threads of execution, this higher-level parallelism is referred to as thread level parallelism.
A thread is a completely independent process with its own set of instructions and data. A thread can represent a process that is part of a parallel program that includes numerous processes, or it can represent a stand-alone program. Each thread has all of the state it needs to run (instructions, data, PC, register state, and so on). Unlike instruction level parallelism, which takes advantage of implicit parallel operations within a loop or straight-line code section, thread level parallelism is expressed directly by the use of numerous naturally parallel threads of execution.
Thread level parallelism is a viable alternative to instruction level parallelism, owing to the fact that it may be more cost-effective to exploit. Thread level parallelism happens naturally in many key applications, including many server applications. Similarly, many applications take advantage of data level parallelism, which allows the same action to be done on several data sets.
Combining these two types of parallelism is a natural alternative because ILP and TLP leverage two separate sorts of parallel structure in a program. Because of the insufficient ILP induced by stalls and dependencies, a lot of functional units on the already-designed datapath are idle. This can be used to take advantage of TLP and keep the functional units active.
Multithreading and its derivatives, such as Simultaneous Multi Threading (SMT) and Chip Multi Processors, are the most common methodologies for utilizing TLP alongside ILP (CMP).
Multithreading: Exploiting Thread-Level Parallelism within a Processor
Multiple threads can share the functional units of a single processor in an overlapping manner thanks to multithreading. To allow this sharing, the CPU must duplicate each thread's separate state. Each thread, for example, requires a separate copy of the register file, a separate PC, and a separate page table.
Multithreading can be approached in two ways.
● Fine-grained multithreading alternates between threads on each instruction, causing numerous threads to execute at the same time. This interleaving is frequently done in a round-robin method, skipping any blocked threads at the time.
● As an alternative to fine-grained multithreading, coarse-grained multithreading was devised. Only on expensive stalls, such as level two cache misses, does coarse-grained multithreading switch threads. Because instructions from other threads will only be delivered when a thread encounters an expensive stall, this change eliminates the need for thread switching to be virtually free and is considerably less likely to slow down the processor.
Simultaneous Multithreading: Converting Thread-Level Parallelism into Instruction-Level Parallelism
Simultaneous multithreading (SMT) is a type of multithreading that takes advantage of the resources of a multi-issue, dynamically-scheduled processor to exploit TLP and ILP at the same time. Modern multiple issue processors frequently have more functional unit parallelism than a single thread can properly employ, which is the primary understanding that underlies SMT. Furthermore, with register renaming and dynamic scheduling, numerous instructions from distinct threads can be issued without respect to their dependencies; the dynamic scheduling capabilities can manage the resolution of the dependencies.
The variations in a processor's capacity to harness the resources of a superscalar are theoretically illustrated in Figure for the following processor configurations:
n a superscalar with no multithreading support,
n a superscalar with coarse-grained multithreading,
n a superscalar with fine-grained multithreading, and
n a superscalar with simultaneous multithreading.

Fig 4: Four different approaches use the issue slots of a superscalar processor
The utilization of issue slots is limited in the superscalar without multithreading capabilities due to a lack of ILP.
The long delays in the coarse-grained multithreaded superscalar are somewhat disguised by switching to another thread that utilizes the processor's resources. The interleaving of threads avoids totally vacant slots in the fine-grained scenario. Because each clock cycle only has one thread issuing instructions.
Thread-level parallelism (TLP) and instruction-level parallelism (ILP) are used simultaneously in the SMT example, with several threads using issue slots in a single clock cycle.
Design Challenges in SMT processors
An SMT processor has a number of design issues, including:
● When working with a bigger register file, numerous contexts were required.
● Maintaining low clock cycle overhead, especially in crucial processes like instruction issue, when more candidate instructions must be considered, and instruction completion, where deciding which instructions to commit can be difficult, and
● Assuring that cache conflicts caused by many threads running at the same time do not degrade performance significantly.
Key takeaway
Thread level parallelism is a viable alternative to instruction level parallelism, owing to the fact that it may be more cost-effective to exploit.
Thread level parallelism happens naturally in many key applications, including many server applications.
A thread is a completely independent process with its own set of instructions and data.
A thread can represent a process that is part of a parallel program that includes numerous processes, or it can represent a stand-alone program
References:
- Computer Architecture: A Quantitative Approach: Hennessy and Patterson: Morgan Kaufmann
- Advanced Computer Architecture, Kai Hwang, McGraw Hill
- Advanced Computer Architectures: A design space approach, Sima D, Fountain T. And Kacsuk P, Pearson Education
- Https://www.tutorialspoint.com/what-are-different-methods-of-parallelism-in-parallel-computer-architecture
- Https://www.cs.umd.edu/~meesh/411/CA-online/chapter/multiple-issue-processors-i/index.html
- Https://www.cs.umd.edu/~meesh/cmsc411/website/projects/dynamic/intro.html
- Https://www.docsity.com/en/branch-prediction-in-advanced-computer-architecture/4556244/