Introduction
A tree data structure can be defined recursively (locally) as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the "children"), with the constraints that no reference is duplicated, and none points to the root.
Definition of TREE:
A tree is defined as a set of one or more nodes T such that:
There is a specially designed node called root node
The remaining nodes are partitioned into N disjoint set of nodes T1, T2,…..Tn, each of which is a tree.

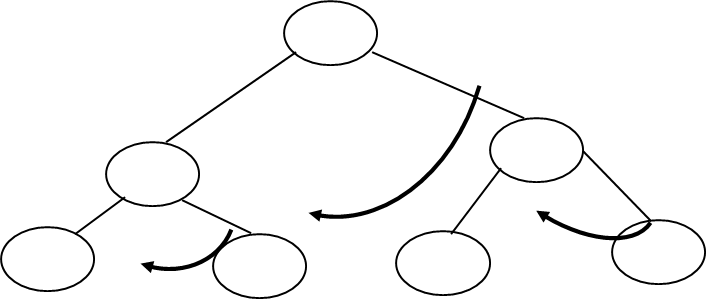
Fig. 4.1 Example of tree
In above tree A is Root.
Remaining nodes are partitioned into three disjoint sets:
{B, E, F}, {C, G, H}, {D}.
All these sets satisfies the properties of tree.
Some examples of TREE and NOT TREE

Each linear list is trivially a tree
Not a tree: cycle A→A
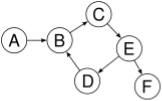
Not a tree: cycle B→C→E→D→B

Not a tree: two non-(connected parts, A→B and C→D→E
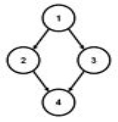
Not a tree: undirected cycle 1-2-4-3
Fig. Examples of tree and no tree
Tree Terminologies
A binary tree is a special cas eof tree in which no node of a tree can have degree more than two.
Definition of Binary Tree:
A binary tree is made of nodes, where each node contains a "left" pointer, a "right" pointer, and a data element. The "root" pointer points to the topmost node in the tree. The left and right pointers recursively point to smaller "subtrees" on either side. A null pointer represents a binary tree with no elements -- the empty tree.
The formal recursive definition is A binary tree is either empty (represented by a null pointer), or is made of a single node, where the left and right pointers (recursive definition ahead) each point to a binary tree.
Example of Binary Tree:

Fig.Example of Binary Tree
Types of Binary Tree,
1. Left Skewed Binary Tree:
2. Right Skewed Binary Tree:
1. Left Skewed Binary Tree:

Fig. 4.6 Example of Left Skewed Binary Tree
In this tree, every node is having only Left sub tree.
2. Right Skewed Binary Tree:

Fig. Example of Right Skewed Binary Tree
In this tree, every node is having only Right sub tree.
Full or strict Binary Tree:
It is a binary tree of depth K having 2k-1 nodes.
For k=3, number of nodes=7
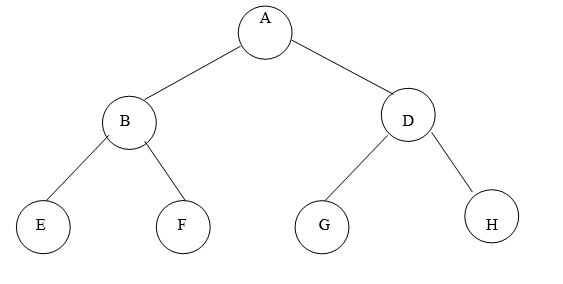
Fig. Example of strict Binary Tree
Complete Binary Tree:
It is a binary tree of depth K with N nodes in which these N nodes can be numbered sequentially from 1 to N.
Since a binary tree is an ordered tree and has levels, it is convenient to assign a number to each node.
Suppose for K=3:
Fig. Example of Complete Binary Tree
The nodes can be numbered sequentially like:
Node number | Node |
1 | A |
2 | B |
3 | D |
4 | E |
5 | F |
Fig. Representation of Complete Binary Tree
Consider another example of binary tree:
Fig. 4.11 Example of Non Complete Binary Tree
If we try to give numbers to nodes it would appear like:
Node number | Node |
1 | A |
2 | B |
3 | D |
4 | - |
5 | - |
6 | E |
7 | F |
Fig. 4.12 Representation of Non Complete Binary Tree
Here nodes cannot be numbers sequentially, so this kind of tree cannot be called as a complete binary tree
Binary Search Tree
We now turn our attention to search tress: Binary Search tress in this chapter and AVL Trees in next chapter. As seen in previous chapter, the array structure provides a very efficient search algorithm, the binary search, but it is inefficient for insertion and deletion algorithms. On the other hand, linked list structure provides efficient insertion and deletion algorithms but it is very inefficient for search algorithm. So what we need is a structure that provides efficient insertion, deletion as well as search algorithms.
Basic Concept:
A Binary Search Tree is a binary tree with the following properties:
1. It may be empty and every node has an identifier.
2. All nodes in left subtree are less than the root.
2. All nodes in right subtree are greater than the root.
4. Each subtree is itself a BST.
Examples of BST:
Valid BSTs:
Fig. Examples of Valid BSTs
Invalid BSTs:

Fig.Examples of Invalid BSTs
Examine the BSTs in Fig.4.2. The first tree, Fig.4.2 (a) breaks the second rule: The left node 30 is greater than that of its root node 20. The second tree, Fig.4.2 (b) breaks the third rule: The right node 20 is less than that of its root node 50. The third tree, Fig.4.2 (c) breaks the second rule: The left node 25 is greater than that of its root node 10. It also breaks the third rule: The right node 08 is less than that of its root node 15.
Threaded Binary Tree
Binary trees, including binary search trees and their variants, can be used to store a set of items in a particular order. For example, a binary search tree assumes data items are ordered and maintain this ordering as part of their insertion and deletion algorithms. One useful operation on such a tree is traversal: visiting the items in the order in which they are stored .A simple recursive traversal algorithm that visits each node of a BST is the following. Assume t is a pointer to a node, or NULL.
Algorithm traverse_tree (root):
Input: a pointer root to a node (or NULL.)
If root = NULL, return.
Else
traverse_tree (left-child (root))
Visit t
traverse_tree (right-child (root))
The problem with this algorithm is that, because of its recursion, it uses stack space proportional to the height of a tree. If the tree is fairly balanced, this amounts to O(log n) space for a tree containing n elements.
One of the solutions to this problem is tree threading.
A threaded binary tree defined as follows:
It is also possible to discover the parent of a node from a threaded binary tree, without explicit use of parent pointers or a stack. This can be useful where stack space is limited, or where a stack of parent pointers is unavailable (for finding the parent pointer via DFS).
Inorder Threaded Binary Tree:
In inorder threaded binary tree, left thread points to the predecessor and right thread points to the successor.
Types Inorder Threaded Binary Tree:
Right Inorder Threaded Binary Tree.
In this type of TBT, only right threads are shown which points to the successor.
Left Inorder Threaded Binary Tree.
In this type of TBT, only left threads are shown which points to the predecessor.
For TBT it is not necessary that the tree must be BST, it can be applied to general tree.
Example: Draw inorder TBT for following data:
10, 8, 1 5, 7, 9, 12, 18
Solution:
Step 1: The general for given data is:
1
8 1
7 9 1 1
Step 2: Write inorder sequence for the above tree:
7, 8, 9, 10, 12, 15, 18
Step 3: Make groups containing three nodes per group like:

Step 4: It means right thread of 7 point to 8 provided that 7 node is not having right link, means right link of 7 is NULL and thread is pointing in bottom-up direction and not in top to bottom .
Left thread of 7 and Right thread of 18 will point to head node.
Step 5: Draw TBT with right and left threads.
Head Node
Left Inorder Threaded Binary Tree:
Right Inorder Threaded Binary Tree:

AVL Trees (Adelsion Velski & Landis):
The concept is developed by three persons: Adelsion, Velski and Landis.
Balance Factor:
Balance factor is (Height of left sub tree - Height of right sub tree)
Height Balance Tree:
An empty tree is height balanced. If T is non empty binary tree with TL and TR as left and right sub tress, then T is height balanced if and only if:
TL and TR are height balanced.
HL- HR =1
HL and HR are heights of left and right sub tree.
For ant node in AVL tree Balance factor must be -1 or 0 or 1.
Following rotations are performed on AVL tree if any of the nodes is unbalanced.
1. LL Rotation.
2. LR Rotation.
3. RL Rotation.
4. RR Rotation.
1. LL Rotation:
Count from unbalanced node. First left node becomes the root node.
2. LR Rotation:
Count from unbalanced node. Go for left node and then right node say X. The node X becomes the root node.
3. RL Rotation:
Count from unbalanced node. Go for right node and then left node say X. The node X becomes the root node.
4. RR Rotation:
Count from unbalanced node. First right node becomes the root node.
While inserting data in AVL tree, Follow the property of Binary search tree (left<root<right)
Example: obtain an AVL tree by inserting one integer at a time in following sequence:
150,155,160,115,110,140,120,145,130
Step 1: insert 150
150
Balance factor for 150 is: 0 – 0=0
1500
NO ROTATION IS REQUIRED.
Step 2: insert 155
 150-1
150-1
1550
Balance factor for 150 is: 0 – 1= -1
Both nodes are balanced.
NO ROATION IS REQIURED.
STEP 3: INSERT 160.
 150-2
150-2
 155-1
155-1
1600
Balance factor of 150 is -2. So 150 is unbalanced. Some rotation is required to do 150 as balanced node. Start from 150 towards 160.
 150-2 R
150-2 R
155-1 R
1600
We get RR direction. So we have to perform RR rotation.
In RR rotation, Count from unbalanced node. First right node becomes the root node. So here first R is 155. So 155 will become the root.

 1550
1550
1500 1600
Now all nodes are balanced.
STEP 4: INSERT 115.

 1551
1551
 1501 1600
1501 1600
1150
All nodes are balanced. NO ROTATION IS REQUIRED.
STEP 5: INSERT 110

 1552
1552
 1502 1600
1502 1600
 1151
1151
1100
155 and 150 are unbalanced. Whenever two/more nodes are unbalanced, we have to consider the lowermost node first. i.e.150. move from 150 towards the node causing unbalancing (110)

 1552
1552

 L 1502 1600
L 1502 1600

 L 1151
L 1151
1100
So we have to perform LL Rotation. In LL rotation, Count from unbalanced node. First Left node becomes the root node. So here first L is 115. So 115 will become the root.

 1551
1551

 1150 1600
1150 1600
1100 1500
Now all nodes are balanced.

 STEP 6: INSERT 140 1552
STEP 6: INSERT 140 1552

 115-1 1600
115-1 1600
 1100 1501
1100 1501
1400
155 is unbalanced. Count move from 155 towards the node causing unbalancing (140).

 1552
1552
 L
L

 115-1 1600
115-1 1600
R
 1100 1501
1100 1501
1400
So we have to perform LR Rotation. In LR rotation, Count from unbalanced node(155). Go for left node and then right node (150). 150 will become root node

 1500
1500

 1150 155-1
1150 155-1
1100 1400 1600
Now all nodes are balanced.
STEP 7: INSERT 120

 1501
1501

 115-1 155-1
115-1 155-1
 1100 1401 1600
1100 1401 1600
1200
Now all nodes are balanced.
STEP 7: INSERT 145

 1501
1501

 115-1 155-1
115-1 155-1

 1100 1400 1600
1100 1400 1600
1200 1450
Now all nodes are balanced.
STEP 7: INSERT 130

 1502
1502

 115-2 155-1
115-2 155-1

 1100 1401 1600
1100 1401 1600
 120-1 1450
120-1 1450
1300
Two nodes 150 and 115 are unbalanced. First consider 115. Count move from 115 towards the node causing unbalancing (130).

 1502
1502



 115-2 155-1
115-2 155-1
 R
R

 1100 1401 1600
1100 1401 1600
 L
L
 120-1 1450
120-1 1450
1300
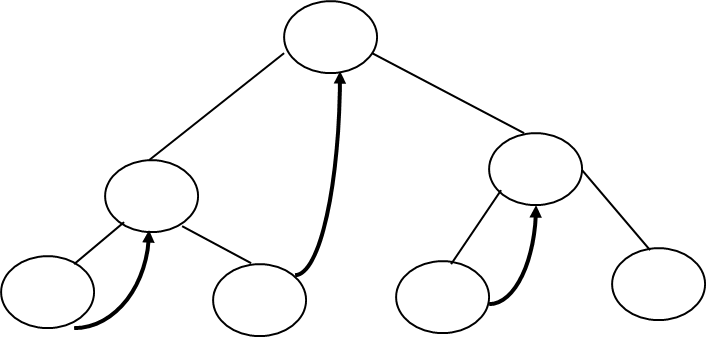
So we have to perform RL Rotation. In RL rotation, Count from unbalanced node(115). Go for Right node and then Left node (120). 120 will become root node.

 1501
1501

 1200 155-1
1200 155-1


 1150 1400 1600
1150 1400 1600
1100 1300 145
Now all nodes are balanced.
Thus the tree is balanced.
Following are the basic operations of a tree −
Node
Define a node having some data, references to its left and right child nodes.
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
Search Operation
Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.
Algorithm
struct node* search(int data){
struct node *current = root;
printf("Visiting elements: ");
while(current->data != data){
if(current != NULL) {
printf("%d ",current->data);
//go to left tree
if(current->data > data){
current = current->leftChild;
} //else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL){
return NULL;
}
}
}
return current;
}
Insert Operation
Whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data.
Algorithm
void insert(int data) {
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
} //go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
Huffman Codes:
Huffman coding is a simple data compression scheme.
Fixed-Length Codes
Suppose we want to compress a 100,000-byte data file that we know contains only the lowercase letters A through F. Since we have only six distinct characters to encode, we can represent each one with three bits rather than the eight bits normally used to store characters:
Letter | A | B | C | D | E | F | |
Codeword | 000 | 001 | 010 | 011 | 100 | 101 | |
This fixed-length code gives us a compression ratio of 5/8 = 62.5%.
Variable-Length Codes
What if we knew the relative frequencies at which each letter occurred? It would be logical to assign shorter codes to the most frequent letters and save longer codes for the infrequent letters. For example, consider this code:
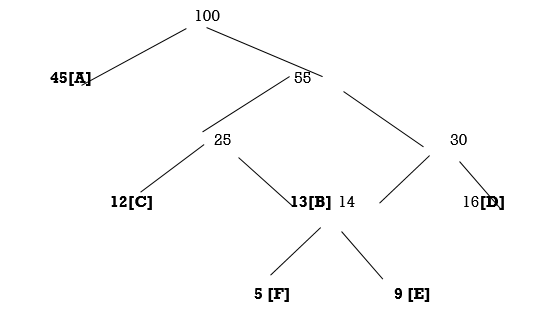
Letter | A | B | C | D | E | F |
Frequency (K) | 45 | 13 | 12 | 16 | 9 | 5 |
Codeword | 0 | 101 | 100 | 111 | 1101 | 1100 |
Using this code, our file can be represented with
(45×1 + 13×3 + 12×3 + 16×3 + 9×4 + 5×4) × 1000 = 224 000 bits
or 28 000 bytes, which gives a compression ratio of 72%. In fact, this is an optimal character code for this file (which is not to say that the file is not further compressible by other means).
Prefix Codes
Notice that in our variable-length code, no codeword is a prefix of any other codeword. For example, we have a codeword 0, so no other codeword starts with 0. And both of our four-bit code words start with 110, which is not a codeword. Such codes are called prefix codes. Prefix codes are useful because they make a stream of bits unambiguous; we simply can accumulate bits from a stream until we have completed a codeword. (Notice that encoding is simple regardless of whether our code is a prefix code: we just build a dictionary of letters to code words, look up each letter we're trying to encode, and append the code words to an output stream.) In turns out that prefix codes always can be used to achieve the optimal compression for a character code, so we're not losing anything by restricting ourselves to this type of character code.
When we're decoding a stream of bits using a prefix code, what data structure might we want to use to help us determine whether we've read a whole codeword yet?
One convenient representation is to use a binary tree with the code words stored in the leaves so that the bits determine the path to the leaf. In our example, the codeword 1100 is found by starting at the root, moving down the right sub tree twice and the left sub tree twice.
Huffman’s algorithm is used to build such type of binary tree.
Algorithm:
Arrange list in ascending order of frequencies.
Create new node with addition of frequencies of first two nodes.
Insert this new node into list and again sort it.
Repeat till only one value remains in the list.
Consider alphabets and their frequencies of occurrences are as:
A | B | C | D | E | F | |
Frequency (K) | 45 | 13 | 12 | 16 | 9 | 5 |
Huffman Algorithm for above data will work like :
Step1: sort the list in ascending order
5 9 12 13 16 45
Step2: New node’s frequency=5+9=14
12 13 14 16 45
Step3: New node’s frequency=12+13=25
14 16 25 45
Step4: New node’s frequency=14+16=30
25 30 45
Step4: New node’s frequency=25+30=55
45 55
Step4: New node’s frequency=45+55=100
100
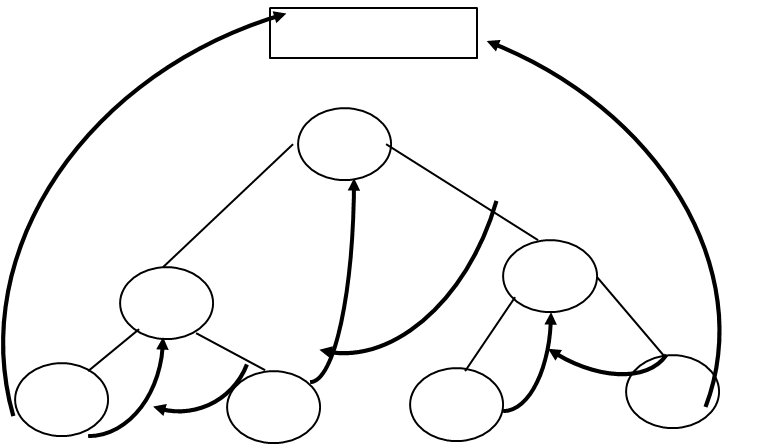
Final Huffman’s tree will be:
Introduction to B-Trees | ||
| ||
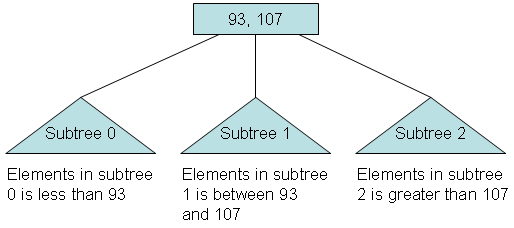
Important properties of a B-tree: B-tree nodes have many more than two children. A B-tree node may contain more than just a single element. The set formulation of the B-tree rules: Every B-tree depends on a positive constant integer called MINIMUM, which is used to determine how many elements are held in a single node. Rule 1: The root can have as few as one element (or even no elements if it also has no children); every other node has at least MINIMUM elements. Rule 2: The maximum number of elements in a node is twice the value of MINIMUM. Rule 3: The elements of each B-tree node are stored in a partially filled array, sorted from the smallest element (at index 0) to the largest element (at the final used position of the array). Rule 4: The number of subtrees below a nonleaf node is always one more than the number of elements in the node. Subtree 0, subtree 1, ... Rule 5: For any nonleaf node:
An element at index i is greater than all the elements in subtree number i of the node, and An element at index i is less than all the elements in subtree number i + 1 of the node. Rule 6: Every leaf in a B-tree has the same depth. Thus it ensures that a B-tree avoids the problem of a unbalanced tree.
|
B+-trees
This leads us to instead imagine storing our rows in a tree structure. Our first instinct would be a balanced binary search tree like a red-black tree, but this really doesn't make much sense for a database since it is stored on disk. You see, disks work by reading and writing whole blocks of data at once — typically 512 bytes or four kilobytes. A node of a binary search tree uses a small fraction of that, so it makes sense to look for a structure that fits more neatly into a disk block.
Hence the B+-tree, in which each node stores up to d references to children and up to d − 1 keys. Each reference is considered “between” two of the node's keys; it references the root of a subtree for which all values are between these two keys.
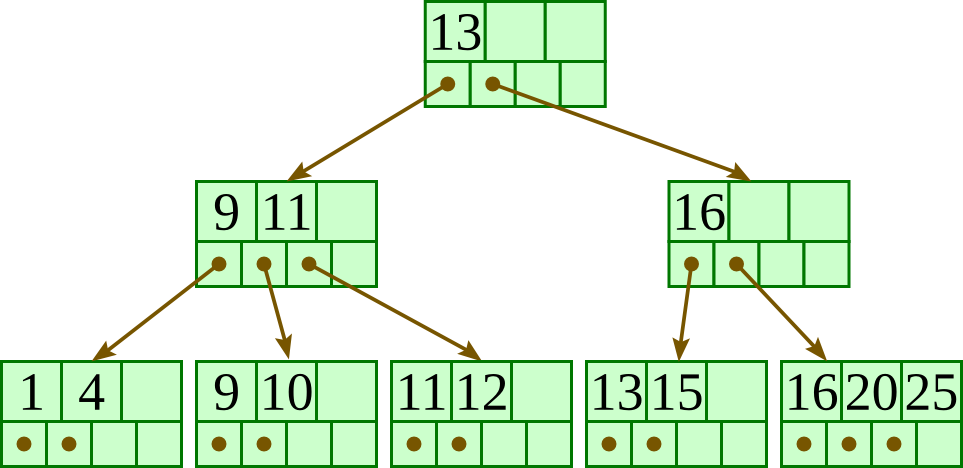
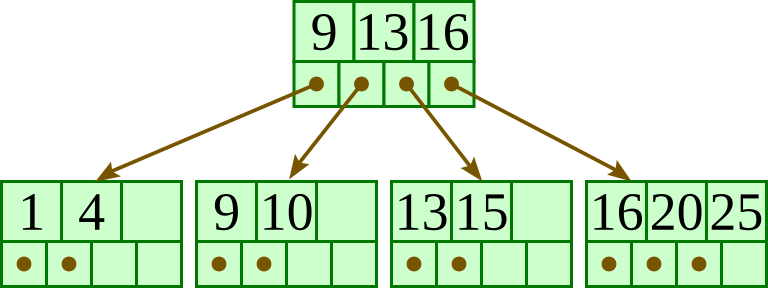
Here is a fairly small tree using 4 as our value for d.
A B+-tree requires that each leaf be the same distance from the root, as in this picture, where searching for any of the 11 values (all listed on the bottom level) will involve loading three nodes from the disk (the root block, a second-level block, and a leaf).
In practice, d will be larger — as large, in fact, as it takes to fill a disk block. Suppose a block is 4KB, our keys are 4-byte integers, and each reference is a 6-byte file offset. Then we'd choose d to be the largest value so that 4 (d − 1) + 6 d ≤ 4096; solving this inequality for d, we end up with d ≤ 410, so we'd use 410 for d. As you can see, d can be large.
A B+-tree maintains the following invariants:
Every node has one more references than it has keys.
All leaves are at the same distance from the root.
For every non-leaf node N with k being the number of keys in N: all keys in the first child's subtree are less than N's first key; and all keys in the ith child's subtree (2 ≤ i ≤ k) are between the (i − 1)th key of n and the ith key of n.
The root has at least two children.
Every non-leaf, non-root node has at least floor(d / 2) children.
Each leaf contains at least floor(d / 2) keys.
Every key from the table appears in a leaf, in left-to-right sorted order.
In our examples, we'll continue to use 4 for d. Looking at our invariants, this requires that each leaf have at least two keys, and each internal node to have at least two children (and thus at least one key).
Insertion algorithm
Descend to the leaf where the key fits.
If the node has an empty space, insert the key/reference pair into the node.
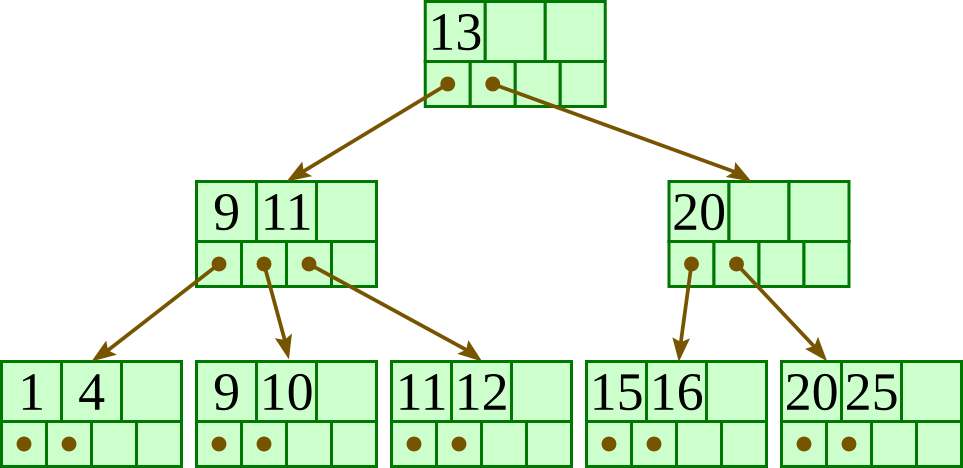
If the node is already full, split it into two nodes, distributing the keys evenly between the two nodes. If the node is a leaf, take a copy of the minimum value in the second of these two nodes and repeat this insertion algorithm to insert it into the parent node. If the node is a non-leaf, exclude the middle value during the split and repeat this insertion algorithm to insert this excluded value into the parent node.
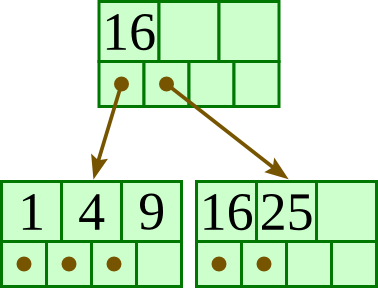
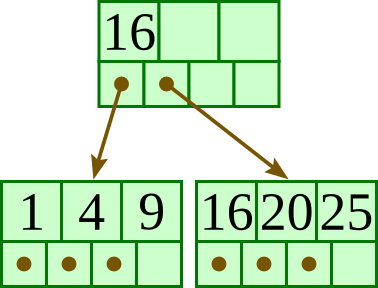
Initial: |
|
Insert 20: |
|
Insert 13: |
|
Insert 15: |
|
Insert 10: |
|
Insert 11: |
|
Insert 12: |
|
Deletion algorithm
Descend to the leaf where the key exists.
Remove the required key and associated reference from the node.
If the node still has enough keys and references to satisfy the invariants, stop.
If the node has too few keys to satisfy the invariants, but its next oldest or next youngest sibling at the same level has more than necessary, distribute the keys between this node and the neighbor. Repair the keys in the level above to represent that these nodes now have a different “split point” between them; this involves simply changing a key in the levels above, without deletion or insertion.
If the node has too few keys to satisfy the invariant, and the next oldest or next youngest sibling is at the minimum for the invariant, then merge the node with its sibling; if the node is a non-leaf, we will need to incorporate the “split key” from the parent into our merging. In either case, we will need to repeat the removal algorithm on the parent node to remove the “split key” that previously separated these merged nodes — unless the parent is the root and we are removing the final key from the root, in which case the merged node becomes the new root (and the tree has become one level shorter than before).
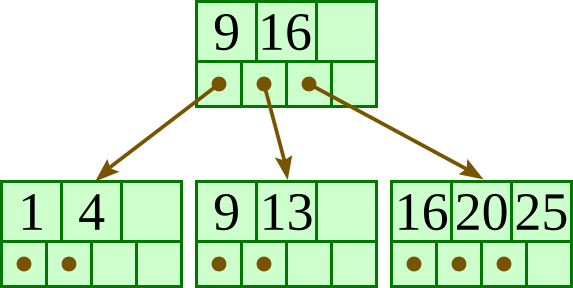
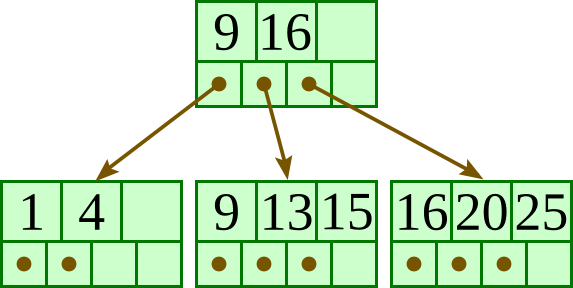
Initial: |
|
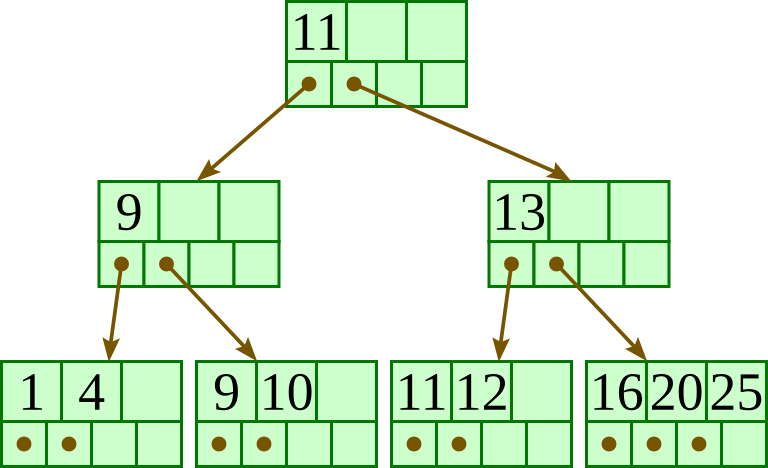
Delete 13: |
|
Delete 15: |
|
Delete 1: |
|
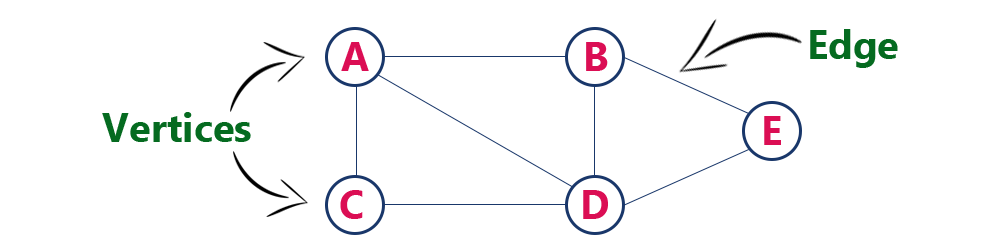
Graph is a collection of vertices and arcs in which vertices are connected with arcs
Graph is a collection of nodes and edges in which nodes are connected with edges
Generally, a graph G is represented as G = ( V , E ), where V is set of vertices and E is set of edges.
Example
The following is a graph with 5 vertices and 6 edges.
This graph G can be defined as G = ( V , E )
Where V = {A,B,C,D,E} and E = {(A,B),(A,C)(A,D),(B,D),(C,D),(B,E),(E,D)}.

Graph Terminology
We use the following terms in graph data structure...
Vertex
Individual data element of a graph is called as Vertex. Vertex is also known as node. In above example graph, A, B, C, D & E are known as vertices.
Edge
An edge is a connecting link between two vertices. Edge is also known as Arc. An edge is represented as (startingVertex, endingVertex). For example, in above graph the link between vertices A and B is represented as (A,B). In above example graph, there are 7 edges (i.e., (A,B), (A,C), (A,D), (B,D), (B,E), (C,D), (D,E)).
Edges are three types.
Undirected Graph
A graph with only undirected edges is said to be undirected graph.
Directed Graph
A graph with only directed edges is said to be directed graph.
Mixed Graph
A graph with both undirected and directed edges is said to be mixed graph.
End vertices or Endpoints
The two vertices joined by edge are called end vertices (or endpoints) of that edge.
Origin
If a edge is directed, its first endpoint is said to be the origin of it.
Destination
If a edge is directed, its first endpoint is said to be the origin of it and the other endpoint is said to be the destination of that edge.
Adjacent
If there is an edge between vertices A and B then both A and B are said to be adjacent. In other words, vertices A and B are said to be adjacent if there is an edge between them.
Incident
Edge is said to be incident on a vertex if the vertex is one of the endpoints of that edge.
Outgoing Edge
A directed edge is said to be outgoing edge on its origin vertex.
Incoming Edge
A directed edge is said to be incoming edge on its destination vertex.
Degree
Total number of edges connected to a vertex is said to be degree of that vertex.
Indegree
Total number of incoming edges connected to a vertex is said to be indegree of that vertex.
Outdegree
Total number of outgoing edges connected to a vertex is said to be outdegree of that vertex.
Parallel edges or Multiple edges
If there are two undirected edges with same end vertices and two directed edges with same origin and destination, such edges are called parallel edges or multiple edges.
Self-loop
Edge (undirected or directed) is a self-loop if its two endpoints coincide with each other.
Simple Graph
A graph is said to be simple if there are no parallel and self-loop edges.
Path
A path is a sequence of alternate vertices and edges that starts at a vertex and ends at other vertex such that each edge is incident to its predecessor and successor vertex.
Depth First Traversal (or Search) for a graph is similar to Depth First Traversal of a tree. The only catch here is, unlike trees, graphs may contain cycles, a node may be visited twice. To avoid processing a node more than once, use a boolean visited array.
Example:
Input: n = 4, e = 6
0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3
Output: DFS from vertex 1 : 1 2 0 3
Explanation:
DFS Diagram:
Input: n = 4, e = 6
2 -> 0, 0 -> 2, 1 -> 2, 0 -> 1, 3 -> 3, 1 -> 3
Output: DFS from vertex 2 : 2 0 1 3
Explanation:
DFS Diagram:


References:
1. Algorithms, Data Structures, and Problem Solving with C++”, Illustrated Edition by Mark Allen Weiss, Addison-Wesley Publishing Company.
2. “How to Solve it by Computer”, 2nd Impression by R.G. Dromey, Pearson Education.
3. “Fundamentals of Data Structures”, Illustrated Edition by Ellis Horowitz, Sartaj Sahni, Computer Science Press.