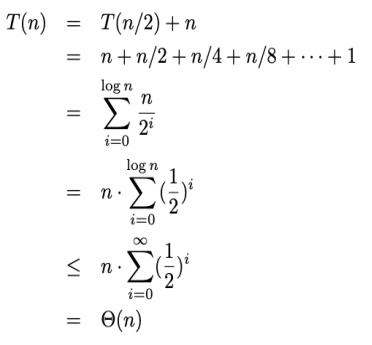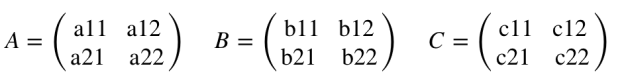Unit-2

Introduction to Divide and Conquer paradigm

2.1 Binary Search

●      It is the searching method where we search an element in the given array

●      Method starts with the middle element.

●      if the key element is smaller than the middle element then it searches the key element into first half of the array ie. Left sub-array.

●      If the key element is greater than the middle element then it searches into the second half of the array ie. Right sub-array.
This process continues until the key element is found. If there is no key element present in the given array then its searches fail.

Algorithm

Algorithms can be implemented as algorithms that are recursive or non-recursive.

Analysis :

●      Input size: Array size, n

●      Basic operation: key comparison

●      Depend on

   Best  –  Matching the key with the middle piece.

   Worst – Often a key is not identified or a key in the list.

●      Let C(n) denote the number of times the fundamental operation is performed. Then one, then Cworst t(n)= Performance in worst case. Since the algorithm after each comparison is the issue is divided into half the size we have,

Cworst (n) = Cworst (n/2) + 1 for n > 1

C(1) = 1

●      Using the master theorem to solve the recurrence equation, to give the number of when the search key is matched against an element in the list, we have:

Application :

1. Guessing Number game
2. Word Lists/Dictionary Quest, etc

Limitations :

1. Interacting badly with the hierarchy of memory
2. Allows the list to be sorted
3. Because of the list element's random access, you need arrays instead of a linked list.

Advantages :

1. Efficient on an incredibly broad list
2. Iteratively/recursively applied can be

Example

Let us explain the following 9 elements of binary search:

The number of comparisons required to check for various components is as follows:

1. Searching for x = 101    low high mid

       1   9    5

       6   9    7

       8   9    8

         9   9    9

        Found

Number of comparison : 4

2. Searching for x = 82    low high mid

       1   9    5

       6   9    7

       8   9    8

        Found

Number of comparison : 3

3. Searching for x = 42    low high mid

       1   9    5

       6   9    7

       6   6    6

         7   6 not Found

Number of comparison : 4

4. Searching for x = -14    low high mid

       1   9    5

       1   4    2

       1   1    1

         2   1 not Found

Number of comparison : 3

The number of element comparisons required to find each of the nine elements continues in this manner:

No part needs seeking more than 4 comparisons. Summarizing the

Comparisons were required for all nine things to be identified and divided by 9, yielding 25/9 . On average, there are around 2.77 comparisons per effective quest.

Depending on the value of x, there are ten possible ways that an un-successful quest will end.

If x < a[1], a[1] < x < a[2], a[2] < x < a[3], a[5] < x < a[6], a[6] < x < a[7] or a[7] < x < a[8] The algorithm requires 3 comparisons of components to decide the 'x'

This isn't present. Binsrch needs 4 part comparisons for all of the remaining choices.

Thus, the average number of comparisons of elements for a failed search is:

(3 + 3 + 3 + 4 + 4 + 3 + 3 + 3 + 4 + 4) / 10 = 34/10 =3.4

The time complexity for a successful search is O(log n) and for an unsuccessful search is Θ(log n).

Key takeaway :

1. It is the searching method where we search an element in the given array
2. if the key element is smaller than the middle element then it searches the key element into first half of the array ie. Left sub-array.

2.2 Quick and Merge sorting techniques

• Quick sort algorithm works on the pivot element.
• Select the pivot element (partitioning element) first. Pivot element can be a random number from a given unsorted array.
• Sort the given array according to pivot as the smaller or equal to pivot comes into the left array and greater than or equal to pivot comes into the right array.
• Now select the next pivot to divide the elements and sort the sub arrays recursively.
        

Features

• Developed by C.A.R. Hoare
• Efficient algorithm
• NOT stable sort
• Significantly faster in practice, than other algorithms     

Algorithm

Analysis of Quick Sort Algorithm         

1. Best case: The pivot which we choose will always be swapped into exactly the middle of the list. And also consider pivot will have an equal number of elements both to its left and right sub arrays.

II.     Worst case: Assume that the pivot partition the list into two parts, so that one of the partitions has no elements while the other has all the other elements.

III.  Average case: Assume that the pivot partition the list into two parts, so that one of the partitions has no elements while the other has all the other elements.

Merge Sort

●      Merge sort consists of two phases as divide and merge.

●      In the divide phase, each time it divides the given unsorted list into two sublists until each sub list gets a single element then sorts the elements.

●      In the merge phase, it merges all the solutions of sub lists and finds the original sorted list.

Features :

●      Is an algorithm dependent on comparison?

●      A stable algorithm is

●      A fine example of the strategy of divide & conquer algorithm design

●      John Von Neumann invented it.

Steps to solve the problem:

Step 1: if the length of the given array is 0 or 1 then it is already sorted, else follow  step 2.

Step 2: split the given unsorted list into two half parts

Step 3: again divide the sub list into two parts until each sub list get single element

Step 4: As each sub list gets the single element compare all the elements with each other & swap in between the elements.

Step 5: merge the elements same as divide phase to get the sorted list

Algorithm:

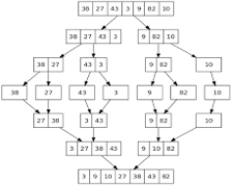
Example :

Apply merge sort for the following list of elements: 38, 27, 43, 3, 9, 82, 10

Analysis of merge sort:

All cases having same efficiency as: O (n log n)

T (n) =T ( n / 2 ) + O ( n )

T (1) = 0

Space requirement: O (n)

Advantages

●      The number of comparisons carried out is almost ideal.

●      Mergesort is never going to degrade to O (n2)

●      It is applicable to files of any size.

Limitations

●      Using extra memory O(n).

Key takeaway :

1. Quick sort algorithm works on the pivot element.
2. Select the pivot element (partitioning element) first. Pivot element can be a random number from a given unsorted array.
3. Sort the given array according to pivot as the smaller or equal to pivot comes into the left array and greater than or equal to pivot comes into the right array.
4. Merge sort consists of two phases as divide and merge.
5. In the divide phase, each time it divides the given unsorted list into two sublists until each sub list gets a single element then sorts the elements.
6. In the merge phase, it merges all the solutions of sub lists and finds the original sorted list.

2.3 Linear time selection algorithm

●      If we could find an element e such that rank(e)= n/2 (the median) in O(n) time, we could make the worst case of fast-sort run in allocation (n log n) time.

●      At the beginning of the partition, we could only swap e with the last element in A and thus make sure that A is always the middle partition.

●      We're going to consider a more general issue than finding the first element:

○      Selection  problem

Select(i) is the i-th element in the order of the elements being sorted.

○      Note: We do not need to sort in order to find Select (i)

○      Note: Pick(1)=minimum, Pick(n)=maximum, Pick(n/2)=median

●      Unique cases of Pick (i)

○      Minimum or limit can be readily found in contrasts between n and 1

■      Scan through elements that maintain minimum/maximum levels

○      You will find the second largest/smallest element in (n-1) + (n-2) = 2n-3 comparisons.

■      Minimum/maximum locate and delete

■      Minimum/maximum Find

○      Median:

■      We can find the median in time using the above concept repeatedly Σn/2i=11(n−i) = n 2/2− Pn/2 i=1 i =n 2/2 − (n/2 · (n/2 + 1))/2 = Θ(n 2 )

■      Using sorting, we can easily build the algorithm '(n log n)

●      Can we develop the time algorithm of O(n) for general I?

●      We could solve the problem if we could partition nicely (which is what we are actually trying to do)

○      By partitioning and then searching for the variable in one of the partitions recursively:

Using Select, select the i'th elements (A, 1, n, i)

●      If the partition was suitable (q = n/2) we have

Note : -

●      The trick is that we resort to one hand only.

●      The algorithm is running in T(n) = T(n − 1) + n = Θ(n 2 ) time in the worst case.

●      We could use randomization to get the partition expected to be fine.

In the worst case, it turns out that we can change the algorithm and get T(n) = Θ(n)

●      The idea is to find a split element q, such that a fraction of the elements are always eliminated:

●      If n’s is the maximum number of elements that we use in the last stage of the algorithm, the runtime is given  T(n) = Θ(n) + T( [n/5 ]) + Θ(n) + T(n’)

2.4 Strassen’s Matrix Multiplication

The standard method of matrix multiplication of two n x n matrices takes T(n) = O(n3).

The following algorithm multiplies nxn matrices A and B:

// Initialize C.

for i = 1 to n

for j = 1 to n

for k = 1 to n

          C [i, j] += A[i, k] * B[k, j];

Strassen’s algorithm is a Divide-and-Conquer algorithm that beats the bound. The usual multiplication of two n x n matrices takes

If C=AB, then we have the following:

c11 = a11 b11 + a12 b21

c12 = a11 b12 + b12 b22

c21 = a21 b11 + a22 b21

c22 = a21 b12 + a22 b22  

8     n/2 * n/2 matrix multiples plus

4     n/2 * n/2 matrix additions

T(n) = 8T(n/2) + O(n2)

Plug in       a = 8, b = 2, k = 2 →logba=3    →   T(n)= O(n3)

Strassen showed how two matrices can be multiplied using only 7 multiplications and 18 additions:

Consider calculating the following 7 products:

q1 = (a11 + a22) * (b11 + b22)

q2 = (a21 + a22) * b11

q3 = a11*( b12 – b22)

q4 = a22 * (b21 – b11)

q5 = (a11 + a12) * b22

q6 = (a21 – a11) * (b11 + b12)

q7 = (a12 – a22) * (b21 + b22)

It turns out that

c11 = q1 + q4 – q5 + q7

c12 = q3 + q5

c21 = q2 + q4

c22 = q1 + q3 – q2 + q6

Code for Implementation of Strassen’s Matrix Multiplication

2.5 Karatsuba Algorithm for fast multiplication

A fast multiplication algorithm that uses a divide and conquer approach to multiply two numbers is the Karatsuba algorithm. Anatoly Karatsuba discovered it in 1960 and published it in 1962.

Given two binary strings representing the value of two integers, find the two string product. For example, the output should be 120 if the first bit string is "1100" and the second bit string is "1010".

For simplicity, let the length be the same for two strings and be n.

One by one, take all bits of the second number and multiply it with all bits of the first number in the naive method. Finally, all multiplications are added. This algorithm takes O(n^2) time.

Using Divide and Conquer, with less time complexity, we can multiply two integers. We divide the numbers given into two halves. Let X and Y be the numbers given.

Let us assume for simplicity that n is even

Xl*2n/2 + Xr [Xl and Xr contain n/2 bits of X on the leftmost and rightmost]

Yl*2n/2 + Yr  [Yl and Yr contain n/2 bits of Y on the leftmost and rightmost]

The product XY can be written as the following :

XY = (Xl*2n/2 + Xr)(Yl*2n/2 + Yr)

      = 2n XlYl + 2n/2(XlYr + XrYl) + XrYr

There are four multiplications of size n/2 if we take a look at the above formula, so we basically divided the size n problem into four subproblems of size n/2. But that does not help, because T(n) = 4T(n/2) + O(n) recurrence solution is O(n^2). The difficult part of this algorithm is to change the middle two terms to some other form so that it would be sufficient for only one extra multiplication.

For the middle two terms, the following is a tricky expression

XlYr + XrYl = (Xl + Xr)(Yl + Yr) - XlYl- XrYr

In this way, the final value of XY becomes

XY = 2n XlYl + 2n/2 * [(Xl + Xr)(Yl + Yr) - XlYl - XrYr] + XrYr

The recurrence becomes T(n) = 3T(n/2) + O(n) with the above trick and O(n) is the solution to this recurrence O(n1.59 ).

What if the input string lengths are different and they are not even? We attach 0's at the beginning to accommodate the different length case. We put floor(n/2) bits in the left half and ceil(n/2) bits in the right half to manage the odd length. So the XY expression switches to the following one.

The algorithm above is referred to as the Karatsuba algorithm and can be used on any basis.

XY = 22ceil(n/2) XlYl + 2ceil(n/2) * [(Xl + Xr)(Yl + Yr) - XlYl - XrYr] + XrYr

Application :

●      In tasks that involve integer multiplication, the Karatsuba algorithm is very effective. For polynomial multiplications, it may also be useful.

●      It is to be remembered that algorithms for faster multiplication exist.

Key takeaway :

1. A fast multiplication algorithm that uses a divide and conquer approach to multiply two numbers is the Karatsuba algorithm.
2. Using Divide and Conquer, with less time complexity, we can multiply two integers.

2.6 Introduction to Heap: Min and Max Heap

Heap is the special tree based data structure in which it has to satisfy the condition of a complete binary tree.

Following are two types of heap:

Max-heap: In this key present at root node must be greater among all key present at all of its children.

A [PARENT (i) ≥A[i]

For all the sub-trees in that binary tree, the same property must be recursively valid. The minimum main factor present at the root is present in a Min-Heap. Below is the binary tree that satisfies all of Min Heap's assets.

Min-heap: In this key present at root node must be minimum among all key present at all of its children.

A [PARENT (i) ≤A[i]

For all the sub-trees in that binary tree, the same property must be recursively valid. The maximum main factor present at the root is in the Max-Heap. Below is the binary tree that satisfies all of Min Heap's assets.

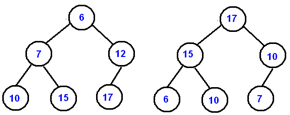
Fig 1: min and max heap

Min-Heap and Max-Heap Output Analysis:

Get Element Maximum or Minimum: O (1)

Insert the Max-Heap or Min-Heap Element: O (log N)

Maximum or Minimum Element Remove: O (log N)

Key takeaway:

1. Heap is the special tree based data structure in which it has to satisfy the condition of a complete binary tree.
2. The key present at the root node in a Min-Heap must be less than or equal to the keys present in all of its children.
3. The key present at the root node in a Max-Heap must be greater than or equal to the keys present in all of its children.

2.7 Build Heap

BUILDHEAP (array A, int n)

 for i ← n/2 down to 1

 do

 HEAPIFY (A, i, n)

Heap-Sort Algorithm 

HEAP-SORT (A)

BUILD-MAX-HEAP (A)

For I ← length[A] down to Z

Do exchange A [1] ←→ A [i]

Heap-size [A] ← heap-size [A]-1

MAX-HEAPIFY (A,1)

Analysis :

Building a max-heap requires O(n) run time. The Heap Sort algorithm makes a call to 'Construct Max-Heap' that we use to address a new heap with O(n) time & each of the (n-1) calls to Max-heap. We know it takes time to 'Max-Heapify' O (log n).

The total running time of Heap-Sort is O (n log n).

2.8 Heap Sort

Heap Sort is one of the best in-place sorting strategies with no worst-case quadratic runtime. Heap sort requires the creation of a Heap data structure from the specified array and then the use of the Heap to sort the array.

You should be wondering how it can help to sort the array by converting an array of numbers into a heap data structure. To understand this, let's begin by knowing what a heap is.

Heap is a unique tree-based data structure that meets the following special heap characteristics:

1. Shape property : The structure of Heap data is always a Complete Binary Tree, which means that all tree levels are fully filled.

2.     Heap property : Every node is either greater or equal to, or less than, or equal to, each of its children. If the parent nodes are larger than their child nodes, the heap is called Max-Heap, and the heap is called Min-Heap if the parent nodes are smaller than their child nodes.

The Heap sorting algorithm is split into two basic components:

●      Creating an unsorted list/array heap.

●      By repeatedly removing the largest/smallest element from the heap, and inserting it into the array, a sorted array is then created.

Complexity analysis of heap sort

Time complexity :

●      Worst case : O(n*log n)

●      Best case : O(n*log n)

●      Average case : O(n*log n)

Space complexity : O(1)

Key takeaway :

1. Heap Sort is one of the best in-place sorting strategies with no worst-case quadratic runtime.
2. Heap Sort is very fast and for sorting it is widely used.
3. Heap sorting is not a stable type, and requires constant space to sort a list.

References:

1. Horowitz & Sahani, "Fundamentals of Computer Algorithm", Galgotia.
2. Algorithm Design: Foundations, Analysis, and Internet Examples, Second Edition, Michael T Goodrich and Roberto Tamassia, Wiley.