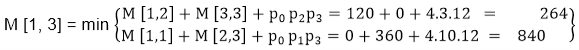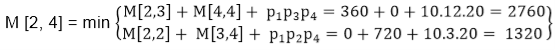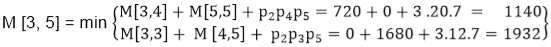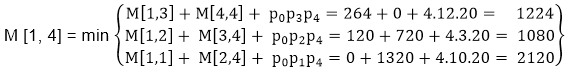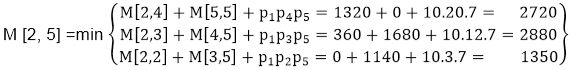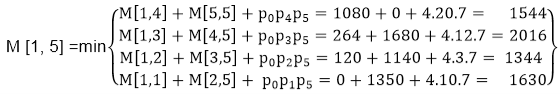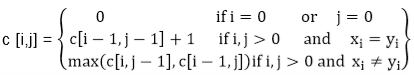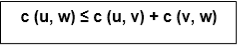UNIT-3

Overview of Brute-Force

3.1 Overview of Brute-Force

Algorithm: 
An algorithm is a step-by-step procedure to solve a problem. A good algorithm should be optimized in terms of time and space. Different types of problems require different types of algorithmic-techniques to be solved in the most optimized manner. There are many types of algorithms but the most important and the fundamental algorithms that you must know will be discussed in this article.

Brute Force Algorithm: 

This is the most basic and simplest type of algorithm. A Brute Force Algorithm is the straightforward approach to a problem i.e., the first approach that comes to our mind on seeing the problem. More technically it is just like iterating every possibility available to solve that problem.

For Example: If there is a lock of 4-digit PIN. The digits to be chosen from 0-9 then the brute force will be trying all possible combinations one by one like 0001, 0002, 0003, 0004, and so on until we get the right PIN. In the worst case, it will take 10,000 tries to find the right combination.

Recursive Algorithm:

This type of algorithm is based on recursion. In recursion, a problem is solved by breaking it into subproblems of the same type and calling own self again and again until the problem is solved with the help of a base condition.

Some common problem that is solved using recursive algorithms are Factorial of a Number, Fibonacci Series, Tower of Hanoi, DFS for Graph, etc.

Divide and Conquer Algorithm:

In Divide and Conquer algorithms, the idea is to solve the problem in two sections, the first section divides the problem into subproblems of the same type. The second section is to solve the smaller problem independently and then add the combined result to produce the final answer to the problem.

Some common problem that is solved using Divide and Conquers Algorithms are Binary Search, Merge Sort, Quick Sort, Strassen’s Matrix Multiplication, etc.

Dynamic Programming Algorithms:

This type of algorithm is also known as the memorization technique because in this the idea is to store the previously calculated result to avoid calculating it again and again. In Dynamic Programming, divide the complex problem into smaller overlapping sub problems and storing the result for future use.

The following problems can be solved using Dynamic Programming algorithm Knapsack Problem, Weighted Job Scheduling, Floyd Warshall Algorithm, Dijkstra Shortest Path Algorithm,etc.

Greedy Algorithm:

In the Greedy Algorithm, the solution is built part by part. The decision to choose the next part is done on the basis that it gives the immediate benefit. It never considers the choices that had taken previously.

Some common problems that can be solved through the Greedy Algorithm are Prim’s Algorithm, Kruskal’s Algorithm, Huffman Coding,etc.

Backtracking Algorithm:

In Backtracking Algorithm, the problem is solved in an incremental way i.e. it is an algorithmic-technique for solving problems recursively by trying to build a solution incrementally, one piece at a time, removing those solutions that fail to satisfy the constraints of the problem at any point of time.

Brute Force Attack

A Brute force attack is a well-known breaking technique, by certain records, brute force attacks represented five percent of affirmed security ruptures. A brute force attack includes ‘speculating’ username and passwords to increase unapproved access to a framework. Brute force is a straightforward attack strategy and has a high achievement rate.

A few attackers use applications and contents as brute force devices. These instruments evaluate various secret word mixes to sidestep confirmation forms. In different cases, attackers attempt to get to web applications via scanning for the correct session ID. Attacker inspiration may incorporate taking data, contaminating destinations with malware, or disturbing help.

While a few attackers still perform brute force attacks physically, today practically all brute force attacks are performed by bots. Attackers have arrangements of usually utilized accreditations, or genuine client qualifications, got through security breaks or the dull web. Bots deliberately attack sites and attempt these arrangements of accreditations, and advise the attacker when they obtain entrance.

Types of Brute Force Attacks:

1. Dictionary attacks – surmises usernames or passwords utilizing a dictionary of potential strings or phrases.
2. Rainbow table attacks – a rainbow table is a precomputed table for turning around cryptographic hash capacities. It very well may be utilized to figure a capacity up to a specific length comprising of a constrained arrangement of characters.
3. Reverse brute force attack – utilizes a typical password or assortment of passwords against numerous conceivable usernames. Focuses on a network of clients for which the attackers have recently acquired information.
4. Hybrid brute force attacks – begins from outer rationale to figure out which password variety might be destined to succeed, and afterward proceeds with the simple way to deal with attempt numerous potential varieties.
5. Simple brute force attack – utilizes an efficient way to deal with ‘surmise’ that doesn’t depend on outside rationale.
6. Credential stuffing – utilizes beforehand known password-username sets, attempting them against numerous sites. Adventures the way that numerous clients have the equivalent username and password across various frameworks.

How to Prevent Brute Force Password Hacking ?

To protect your organization from brute force password hacking, enforce the use of strong passwords.

Passwords should:

• Never use information that can be found online (like names of family members).
• Have as many characters as possible.
• Combine letters, numbers, and symbols.
• Avoid common patterns.
• Be different for each user account.
• Change your password periodically
• Use strong and long password
• Use multifactor authentication

Key takeaway

Brute Force Algorithm: 

This is the most basic and simplest type of algorithm. A Brute Force Algorithm is the straightforward approach to a problem i.e., the first approach that comes to our mind on seeing the problem. More technically it is just like iterating every possibility available to solve that problem.

For Example: If there is a lock of 4-digit PIN. The digits to be chosen from 0-9 then the brute force will be trying all possible combinations one by one like 0001, 0002, 0003, 0004, and so on until we get the right PIN. In the worst case, it will take 10,000 tries to find the right combination.

3.2 Greedy Programming

"Greedy Method finds out of many options, but you have to choose the best option."

In this method, we have to find out the best method/option out of many present ways.

In this approach/method we focus on the first stage and decide the output, don't think about the future.

This method may or may not give the best output.

Greedy Algorithm solves problems by making the best choice that seems best at the particular moment. Many optimization problems can be determined using a greedy algorithm. Some issues have no efficient solution, but a greedy algorithm may provide a solution that is close to optimal. A greedy algorithm works if a problem exhibits the following two properties:

1. Greedy Choice Property: A globally optimal solution can be reached at by creating a locally optimal solution. In other words, an optimal solution can be obtained by creating "greedy" choices.
2. Optimal substructure: Optimal solutions contain optimal subsolutions. In other words, answers to subproblems of an optimal solution are optimal.

Example:

1. machine scheduling
2. Fractional Knapsack Problem
3. Minimum Spanning Tree
4. Huffman Code
5. Job Sequencing
6. Activity Selection Problem

Steps for achieving a Greedy Algorithm are:

1. Feasible: Here we check whether it satisfies all possible constraints or not, to obtain at least one solution to our problems.
2. Local Optimal Choice: In this, the choice should be the optimum which is selected from the currently available
3. Unalterable: Once the decision is made, at any subsequence step that option is not altered.

An Activity Selection Problem

The activity selection problem is a mathematical optimization problem. Our first illustration is the problem of scheduling a resource among several challenge activities. We find a greedy algorithm provides a well designed and simple method for selecting a maximum- size set of manually compatible activities.

Suppose S = {1, 2....n} is the set of n proposed activities. The activities share resources which can be used by only one activity at a time, e.g., Tennis Court, Lecture Hall, etc. Each Activity "i" has start time si and a finish time fi, where si ≤fi. If selected activity "i" take place meanwhile the half-open time interval [si,fi). Activities i and j are compatible if the intervals (si, fi) and [si, fi) do not overlap (i.e. i and j are compatible if si ≥fi or si ≥fi). The activity-selection problem chosen the maximum- size set of mutually consistent activities.

Algorithm Of Greedy- Activity Selector:

GREEDY- ACTIVITY SELECTOR (s, f)

1. n ← length [s]

2. A ← {1}

3. j ← 1.

4. for i ← 2 to n

5. do if si ≥ fi

6. then A ← A ∪ {i}

7. j ← i

8. return A

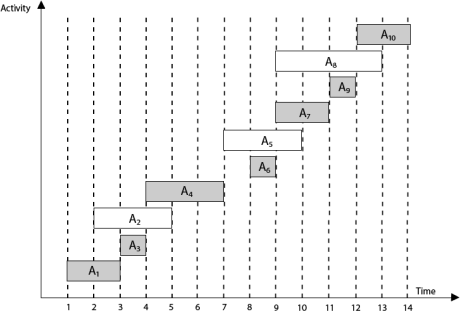
Example: Given 10 activities along with their start and end time as

S = (A1 A2 A3 A4 A5 A6 A7 A8 A9 A10)

Si = (1,2,3,4,7,8,9,9,11,12)

fi = (3,5,4,7,10,9,11,13,12,14)

Compute a schedule where the greatest number of activities takes place.

Solution: The solution to the above Activity scheduling problem using a greedy strategy is illustrated below:

Arranging the activities in increasing order of end time

Now, schedule A1

Next schedule A3 as A1 and A3 are non-interfering.

Next skip A2 as it is interfering.

Next, schedule A4 as A1 A3 and A4 are non-interfering, then next, schedule A6 as A1 A3 A4 and A6 are non-interfering.

Skip A5 as it is interfering.

Next, schedule A7 as A1 A3 A4 A6 and A7 are non-interfering.

Next, schedule A9 as A1 A3 A4 A6 A7 and A9 are non-interfering.

Skip A8 as it is interfering.

Next, schedule A10 as A1 A3 A4 A6 A7 A9 and A10 are non-interfering.

Thus the final Activity schedule is:

Key takeaway

"Greedy Method finds out of many options, but you have to choose the best option."

In this method, we have to find out the best method/option out of many present ways.

In this approach/method we focus on the first stage and decide the output, don't think about the future.

This method may or may not give the best output.

3.3 Dynamic Programming

Dynamic Programming is the most powerful design technique for solving optimization problems.

Divide & Conquer algorithm partition the problem into disjoint subproblems solve the subproblems recursively and then combine their solution to solve the original problems.

Dynamic Programming is used when the subproblems are not independent, e.g. when they share the same subproblems. In this case, divide and conquer may do more work than necessary, because it solves the same sub problem multiple times.

Dynamic Programming solves each subproblems just once and stores the result in a table so that it can be repeatedly retrieved if needed again.

Dynamic Programming is a Bottom-up approach- we solve all possible small problems and then combine to obtain solutions for bigger problems.

Dynamic Programming is a paradigm of algorithm design in which an optimization problem is solved by a combination of achieving sub-problem solutions and appearing to the "principle of optimality".

Characteristics of Dynamic Programming:

Dynamic Programming works when a problem has the following features:-

Fig 1 - Characteristics of Dynamic Programming

• Optimal Substructure: If an optimal solution contains optimal sub solutions then a problem exhibits optimal substructure.
• Overlapping subproblems: When a recursive algorithm would visit the same subproblems repeatedly, then a problem has overlapping subproblems.

If a problem has optimal substructure, then we can recursively define an optimal solution. If a problem has overlapping subproblems, then we can improve on a recursive implementation by computing each subproblem only once.

If a problem doesn't have optimal substructure, there is no basis for defining a recursive algorithm to find the optimal solutions. If a problem doesn't have overlapping sub problems, we don't have anything to gain by using dynamic programming.

If the space of subproblems is enough (i.e. polynomial in the size of the input), dynamic programming can be much more efficient than recursion.

Elements of Dynamic Programming

There are basically three elements that characterize a dynamic programming algorithm:-

Fig 2 - Elements of Dynamic Programming

1. Substructure: Decompose the given problem into smaller subproblems. Express the solution of the original problem in terms of the solution for smaller problems.
2. Table Structure: After solving the sub-problems, store the results to the sub problems in a table. This is done because subproblem solutions are reused many times, and we do not want to repeatedly solve the same problem over and over again.
3. Bottom-up Computation: Using table, combine the solution of smaller subproblems to solve larger subproblems and eventually arrives at a solution to complete problem.

Note: Bottom-up means:-

1. Start with smallest subproblems.
2. Combining their solutions obtain the solution to sub-problems of increasing size.
3. Until solving at the solution of the original problem.

Components of Dynamic programming

Fig 3 - Components of Dynamic programming

1. Stages: The problem can be divided into several subproblems, which are called stages. A stage is a small portion of a given problem. For example, in the shortest path problem, they were defined by the structure of the graph.
2. States: Each stage has several states associated with it. The states for the shortest path problem was the node reached.
3. Decision: At each stage, there can be multiple choices out of which one of the best decisions should be taken. The decision taken at every stage should be optimal; this is called a stage decision.
4. Optimal policy: It is a rule which determines the decision at each stage; a policy is called an optimal policy if it is globally optimal. This is known as Bellman principle of optimality.
5. Given the current state, the optimal choices for each of the remaining states does not depend on the previous states or decisions. In the shortest path problem, it was not necessary to know how we got a node only that we did.
6. There exist a recursive relationship that identify the optimal decisions for stage j, given that stage j+1, has already been solved.
7. The final stage must be solved by itself.

Development of Dynamic Programming Algorithm

It can be broken into four steps:

1. Characterize the structure of an optimal solution.
2. Recursively defined the value of the optimal solution. Like Divide and Conquer, divide the problem into two or more optimal parts recursively. This helps to determine what the solution will look like.
3. Compute the value of the optimal solution from the bottom up (starting with the smallest subproblems)
4. Construct the optimal solution for the entire problem form the computed values of smaller subproblems.

Applications of dynamic programming

1. 0/1 knapsack problem
2. Mathematical optimization problem
3. All pair Shortest path problem
4. Reliability design problem
5. Longest common subsequence (LCS)
6. Flight control and robotics control
7. Time-sharing: It schedules the job to maximize CPU usage

Key takeaway

1. Dynamic Programming is the most powerful design technique for solving optimization problems.
2. Divide & Conquer algorithm partition the problem into disjoint subproblems solve the subproblems recursively and then combine their solution to solve the original problems.
3. Dynamic Programming is used when the subproblems are not independent, e.g. when they share the same subproblems. In this case, divide and conquer may do more work than necessary, because it solves the same sub problem multiple times.
4. Dynamic Programming solves each subproblems just once and stores the result in a table so that it can be repeatedly retrieved if needed again.

3.4 Branch and Bound and back tracking methodologies

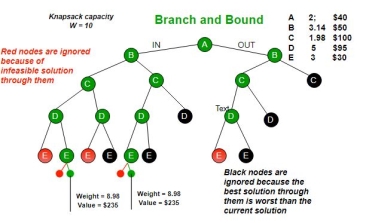
Branch and bound is an algorithm design paradigm which is generally used for solving combinatorial optimization problems. These problems are typically exponential in terms of time complexity and may require exploring all possible permutations in worst case. The Branch and Bound Algorithm technique solves these problems relatively quickly.

Let us consider the 0/1 Knapsack problem to understand Branch and Bound.

There are many algorithms by which the knapsack problem can be solved:

Greedy Algorithm for Fractional Knapsack

DP solution for 0/1 Knapsack

Backtracking Solution for 0/1 Knapsack.

Let’s see the Branch and Bound Approach to solve the 0/1 Knapsack problem: The Backtracking Solution can be optimized if we know a bound on best possible solution subtree rooted with every node. If the best in subtree is worse than current best, we can simply ignore this node and its subtrees. So we compute bound (best solution) for every node and compare the bound with current best solution before exploring the node.

Example bounds used in below diagram are, A down can give $315, B down can $275, C down can $225, D down can $125 and E down can $30.

Key takeaway

1. Branch and bound is an algorithm design paradigm which is generally used for solving combinatorial optimization problems. These problems are typically exponential in terms of time complexity and may require exploring all possible permutations in worst case. The Branch and Bound Algorithm technique solves these problems relatively quickly.

3.5 Greedy paradigm examples of exact optimization solution

In Greedy Algorithm a set of resources are recursively divided based on the maximum, immediate availability of that resource at any given stage of execution.

To solve a problem based on the greedy approach, there are two stages

1. Scanning the list of items
2. Optimization

These stages are covered parallelly in this Greedy algorithm tutorial, on course of division of the array.

To understand the greedy approach, you will need to have a working knowledge of recursion and context switching. This helps you to understand how to trace the code. You can define the greedy paradigm in terms of your own necessary and sufficient statements.

Two conditions define the greedy paradigm.

• Each stepwise solution must structure a problem towards its best-accepted solution.
• It is sufficient if the structuring of the problem can halt in a finite number of greedy steps.

With the theorizing continued, let us describe the history associated with the Greedy search approach.

History of Greedy Algorithms

Here is an important landmark of greedy algorithms:

• Greedy algorithms were conceptualized for many graph walk algorithms in the 1950s.
• Esdger Djikstra conceptualized the algorithm to generate minimal spanning trees. He aimed to shorten the span of routes within the Dutch capital, Amsterdam.
• In the same decade, Prim and Kruskal achieved optimization strategies that were based on minimizing path costs along weighed routes.
• In the '70s, American researchers, Cormen, Rivest, and Stein proposed a recursive substructuring of greedy solutions in their classical introduction to algorithms book.
• The Greedy search paradigm was registered as a different type of optimization strategy in the NIST records in 2005.
• Till date, protocols that run the web, such as the open-shortest-path-first (OSPF) and many other network packet switching protocols use the greedy strategy to minimize time spent on a network.

Greedy Strategies and Decisions

Logic in its easiest form was boiled down to "greedy" or "not greedy". These statements were defined by the approach taken to advance in each algorithm stage.

For example, Djikstra's algorithm utilized a stepwise greedy strategy identifying hosts on the Internet by calculating a cost function. The value returned by the cost function determined whether the next path is "greedy" or "non-greedy".

In short, an algorithm ceases to be greedy if at any stage it takes a step that is not locally greedy. The Greedy problems halt with no further scope of greed.

Characteristics of the Greedy Approach

The important characteristics of a Greedy method algorithm are:

• There is an ordered list of resources, with costs or value attributions. These quantify constraints on a system.
• You will take the maximum quantity of resources in the time a constraint applies.
• For example, in an activity scheduling problem, the resource costs are in hours, and the activities need to be performed in serial order.

Fig 4 – Greedy method approach

Why use the Greedy Approach?

Here are the reasons for using the greedy approach:

• The greedy approach has a few tradeoffs, which may make it suitable for optimization.
• One prominent reason is to achieve the most feasible solution immediately. In the activity selection problem (Explained below), if more activities can be done before finishing the current activity, these activities can be performed within the same time.
• Another reason is to divide a problem recursively based on a condition, with no need to combine all the solutions.
• In the activity selection problem, the "recursive division" step is achieved by scanning a list of items only once and considering certain activities.

How to Solve the activity selection problem

In the activity scheduling example, there is a "start" and "finish" time for every activity. Each Activity is indexed by a number for reference. There are two activity categories.

1. considered activity: is the Activity, which is the reference from which the ability to do more than one remaining Activity is analyzed.
2. remaining activities: activities at one or more indexes ahead of the considered activity.

The total duration gives the cost of performing the activity. That is (finish - start) gives us the durational as the cost of an activity.

You will learn that the greedy extent is the number of remaining activities you can perform in the time of a considered activity.

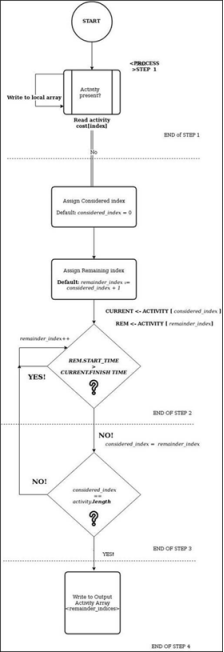
Architecture of the Greedy approach

STEP 1)

Scan the list of activity costs, starting with index 0 as the considered Index.

STEP 2)

When more activities can be finished by the time, the considered activity finishes, start searching for one or more remaining activities.

STEP 3)

If there are no more remaining activities, the current remaining activity becomes the next considered activity. Repeat step 1 and step 2, with the new considered activity. If there are no remaining activities left, go to step 4.

STEP 4 )

Return the union of considered indices. These are the activity indices that will be used to maximize throughput.

Fig 5 - Architecture of the Greedy Approach

Code Explanation

#include<iostream>

#include<stdio.h>

#include<stdlib.h>

#define MAX_ACTIVITIES 12

Explanation of code:

1. Included header files/classes
2. A max number of activities provided by the user.

using namespace std;

class TIME

{

    public:

    int hours;

    public: TIME()

    {

     hours = 0;

    }

};

Explanation of code:

1. The namespace for streaming operations.
2. A class definition for TIME
3. An hour timestamp.
4. A TIME default constructor
5. The hours variable.

class Activity

{

    public:

    int index;

    TIME start;

    TIME finish;

    public: Activity()

    {

     start = finish = TIME();

    }

};

Explanation of code:

1. A class definition from activity
2. Timestamps defining a duration
3. All timestamps are initialized to 0 in the default constructor

class Scheduler

{

    public:

    int considered_index,init_index;

    Activity *current_activities = new    Activity[MAX_ACTIVITIES];

    Activity *scheduled;

Explanation of code:

1. Part 1 of the scheduler class definition.
2. Considered Index is the starting point for scanning the array.
3. The initialization index is used to assign random timestamps.
4. An array of activity objects is dynamically allocated using the new operator.
5. The scheduled pointer defines the current base location for greed.

Scheduler()

{

     considered_index = 0;

     scheduled = NULL;

...

...

Explanation of code:

1. The scheduler constructor - part 2 of the scheduler class definition.
2. The considered index defines the current start of the current scan.
3. The current greedy extent is undefined at the start.

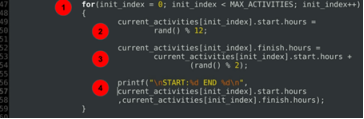
for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++)

 {

      current_activities[init_index].start.hours =

       rand() % 12;

      current_activities[init_index].finish.hours =

       current_activities[init_index].start.hours +

        (rand() % 2);

      printf("\nSTART:%d END %d\n",

      current_activities[init_index].start.hours

      ,current_activities[init_index].finish.hours);

 }

…

…

Explanation of code:

1. A for loop to initialize start hours and end hours of each of the activities currently scheduled.
2. Start time initialization.
3. End time initialization always after or exactly at the start hour.
4. A debug statement to print out allocated durations.

 public:

      Activity * activity_select(int);

};

Explanation of code:

1. Part 4 - the last part of the scheduler class definition.
2. Activity select function takes a starting point index as the base and divides the greedy quest into greedy subproblems.

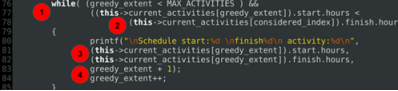
Activity * Scheduler :: activity_select(int considered_index)

{

    this->considered_index = considered_index;

    int greedy_extent = this->considered_index + 1;

…

…

1. Using the scope resolution operator (::), the function definition is provided.
2. The considered Index is the Index called by value. The greedy_extent is the initialized just an index after the considered Index.

Activity * Scheduler :: activity_select(int considered_index)

{

     while( (greedy_extent < MAX_ACTIVITIES ) &&

     ((this->current_activities[greedy_extent]).start.hours <

      (this->current_activities[considered_index]).finish.hours ))

     {

     printf("\nSchedule start:%d \nfinish%d\n activity:%d\n",

     (this->current_activities[greedy_extent]).start.hours,

     (this->current_activities[greedy_extent]).finish.hours,

     greedy_extent + 1);

     greedy_extent++;

     }

…

...

Explanation of code:

1. The core logic- The greedy extent is limited to the number of activities.
2. The start hours of the current Activity are checked as schedulable before the considered Activity (given by considered index) would finish.
3. As long as this possible, an optional debug statement is printed.
4. Advance to next index on the activity array

...

if ( greedy_extent <= MAX_ACTIVITIES )

    {

     return activity_select(greedy_extent);

    }

    else

    {

     return NULL;

    }

}

Explanation of code:

1. The conditional checks if all the activities have been covered.
2. If not, you can restart your greedy with the considered Index as the current point. This is a recursive step that greedily divides the problem statement.
3. If yes, it returns to the caller with no scope for extending greed.

int main()

{

    Scheduler *activity_sched = new Scheduler();

    activity_sched->scheduled = activity_sched->activity_select(

       activity_sched->considered_index);

    return 0;

}

Explanation of code:

1. The main function used to invoke the scheduler.
2. A new Scheduler is instantiated.
3. The activity select function, which returns a pointer of type activity comes back to the caller after the greedy quest is over.

Output:

START:7 END 7

START:9 END 10

START:5 END 6

START:10 END 10

START:9 END 10

Schedule start:5

finish6

 activity:3

Schedule start:9

finish10

 activity:5

Disadvantages of Greedy Algorithms

It is not suitable for Greedy problems where a solution is required for every subproblem like sorting.

In such Greedy algorithm practice problems, the Greedy method can be wrong; in the worst case even lead to a non-optimal solution.

Therefore the disadvantage of greedy algorithms is using not knowing what lies ahead of the current greedy state.

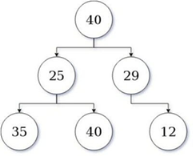
Below is a depiction of the disadvantage of the Greedy method:

Fig 5 - Depiction of the disadvantage of the Greedy method

In the greedy scan shown here as a tree (higher value higher greed), an algorithm state at value: 40, is likely to take 29 as the next value. Further, its quest ends at 12. This amounts to a value of 41.

However, if the algorithm took a sub-optimal path or adopted a conquering strategy. then 25 would be followed by 40, and the overall cost improvement would be 65, which is valued 24 points higher as a suboptimal decision.

Examples of Greedy Algorithms

Most networking algorithms use the greedy approach. Here is a list of few Greedy algorithm examples:

• Prim's Minimal Spanning Tree Algorithm
• Travelling Salesman Problem
• Graph - Map Coloring
• Kruskal's Minimal Spanning Tree Algorithm
• Dijkstra's Minimal Spanning Tree Algorithm
• Graph - Vertex Cover
• Knapsack Problem
• Job Scheduling Problem

Summary:

To summarize, the article defined the greedy paradigm, showed how greedy optimization and recursion, can help you obtain the best solution up to a point. The Greedy algorithm is widely taken into application for problem solving in many languages as Greedy algorithm Python, C, C#, PHP, Java, etc. The activity selection of Greedy algorithm example was described as a strategic problem that could achieve maximum throughput using the greedy approach. In the end, the demerits of the usage of the greedy approach were explained.

Key takeaway

In Greedy Algorithm a set of resources are recursively divided based on the maximum, immediate availability of that resource at any given stage of execution.

To solve a problem based on the greedy approach, there are two stages

1. Scanning the list of items
2. Optimization

These stages are covered parallelly in this Greedy algorithm tutorial, on course of division of the array.

To understand the greedy approach, you will need to have a working knowledge of recursion and context switching. This helps you to understand how to trace the code. You can define the greedy paradigm in terms of your own necessary and sufficient statements.

3.6 Minimum Cost Spanning Tree

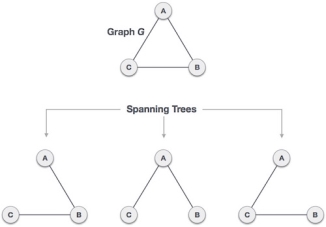
A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected..

By this definition, we can draw a conclusion that every connected and undirected Graph G has at least one spanning tree. A disconnected graph does not have any spanning tree, as it cannot be spanned to all its vertices.

Fig 6 – Spanning Tree

We found three spanning trees off one complete graph. A complete undirected graph can have maximum nn-2 number of spanning trees, where n is the number of nodes. In the above addressed example, n is 3, hence 33−2 = 3 spanning trees are possible.

General Properties of Spanning Tree

We now understand that one graph can have more than one spanning tree. Following are a few properties of the spanning tree connected to graph G −

• A connected graph G can have more than one spanning tree.
• All possible spanning trees of graph G, have the same number of edges and vertices.
• The spanning tree does not have any cycle (loops).
• Removing one edge from the spanning tree will make the graph disconnected, i.e. the spanning tree is minimally connected.
• Adding one edge to the spanning tree will create a circuit or loop, i.e. the spanning tree is maximally acyclic.

Mathematical Properties of Spanning Tree

• Spanning tree has n-1 edges, where n is the number of nodes (vertices).
• From a complete graph, by removing maximum e - n + 1 edges, we can construct a spanning tree.
• A complete graph can have maximum nn-2 number of spanning trees.

Thus, we can conclude that spanning trees are a subset of connected Graph G and disconnected graphs do not have spanning tree.

Application of Spanning Tree

Spanning tree is basically used to find a minimum path to connect all nodes in a graph. Common application of spanning trees are −

• Civil Network Planning
• Computer Network Routing Protocol
• Cluster Analysis

Let us understand this through a small example. Consider, city network as a huge graph and now plans to deploy telephone lines in such a way that in minimum lines we can connect to all city nodes. This is where the spanning tree comes into picture.

Minimum Spanning Tree (MST)

In a weighted graph, a minimum spanning tree is a spanning tree that has minimum weight than all other spanning trees of the same graph. In real-world situations, this weight can be measured as distance, congestion, traffic load or any arbitrary value denoted to the edges.

Minimum Spanning-Tree Algorithm

We shall learn about two most important spanning tree algorithms here −

• Kruskal's Algorithm
• Prim's Algorithm

Both are greedy algorithms.

Key takeaway

A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected..

By this definition, we can draw a conclusion that every connected and undirected Graph G has at least one spanning tree. A disconnected graph does not have any spanning tree, as it cannot be spanned to all its vertices.

3.7 Knapsack problem

Knapsack is basically means bag. A bag of given capacity.

We want to pack n items in your luggage.

• The ith item is worth vi dollars and weight wi pounds.
• Take as valuable a load as possible, but cannot exceed W pounds.
• vi wi W are integers.

1. W ≤ capacity  
2. Value ← Max  

Input:

• Knapsack of capacity
• List (Array) of weight and their corresponding value.

Output: To maximize profit and minimize weight in capacity.

The knapsack problem where we have to pack the knapsack with maximum value in such a manner that the total weight of the items should not be greater than the capacity of the knapsack.

Knapsack problem can be further divided into two parts:

1. Fractional Knapsack: Fractional knapsack problem can be solved by Greedy Strategy where as 0 /1 problem is not.

It cannot be solved by Dynamic Programming Approach.

0/1 Knapsack Problem:

In this item cannot be broken which means thief should take the item as a whole or should leave it. That's why it is called 0/1 knapsack Problem.

• Each item is taken or not taken.
• Cannot take a fractional amount of an item taken or take an item more than once.
• It cannot be solved by the Greedy Approach because it is enable to fill the knapsack to capacity.
• Greedy Approach doesn't ensure an Optimal Solution.

Example of 0/1 Knapsack Problem:

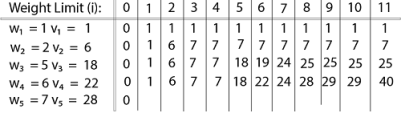
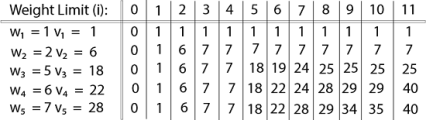
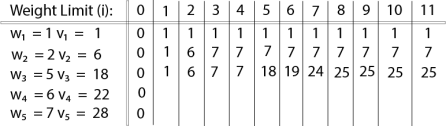
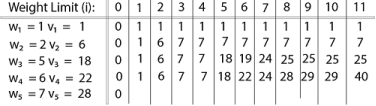
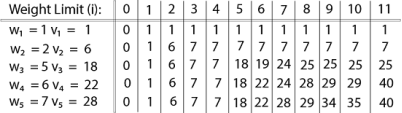
Example: The maximum weight the knapsack can hold is W is 11. There are five items to choose from. Their weights and values are presented in the following table:

The [i, j] entry here will be V [i, j], the best value obtainable using the first "i" rows of items if the maximum capacity were j. We begin by initialization and first row.

The maximum value of items in the knapsack is 40, the bottom-right entry). The dynamic programming approach can now be coded as the following algorithm:

Algorithm of Knapsack Problem

KNAPSACK (n, W)

 1. for w = 0, W

 2. do V [0,w] ← 0

 3. for i=0, n

 4. do V [i, 0] ← 0 

 5. for w = 0, W

 6. do if (wi≤ w & vi + V [i-1, w -  wi]> V [i -1,W])

 7. then V [i, W] ← vi + V [i - 1, w - wi]

 8. else V [i, W] ← V [i - 1, w]

Key takeaway

Knapsack is basically means bag. A bag of given capacity.

We want to pack n items in your luggage.

• The ith item is worth vi dollars and weight wi pounds.
• Take as valuable a load as possible, but cannot exceed W pounds.
• vi wi W are integers.

3.     W ≤ capacity  

4.     Value ← Max  

Input:

• Knapsack of capacity
• List (Array) of weight and their corresponding value.

Output: To maximize profit and minimize weight in capacity.

3.8 Job Sequencing Problem

Problem Statement

In job sequencing problem, the objective is to find a sequence of jobs, which is completed within their deadlines and gives maximum profit.

Solution

Let us consider, a set of n given jobs which are associated with deadlines and profit is earned, if a job is completed by its deadline. These jobs need to be ordered in such a way that there is maximum profit.

It may happen that all of the given jobs may not be completed within their deadlines.

Assume, deadline of ith job Ji is di and the profit received from this job is pi. Hence, the optimal solution of this algorithm is a feasible solution with maximum profit.

Thus, D(i)>0

for 1⩽i⩽n

.Initially, these jobs are ordered according to profit, i.e. p1⩾p2⩾p3⩾...⩾pn

.Algorithm: Job-Sequencing-With-Deadline (D, J, n, k)

D(0) := J(0) := 0

k := 1

J(1) := 1   // means first job is selected

for i = 2 … n do

   r := k

   while D(J(r)) > D(i) and D(J(r)) ≠ r do

      r := r – 1

   if D(J(r)) ≤ D(i) and D(i) > r then

      for l = k … r + 1 by -1 do

         J(l + 1) := J(l)

         J(r + 1) := i

         k := k + 1

Analysis

In this algorithm, we are using two loops, one is within another. Hence, the complexity of this algorithm is O(n2)

Example

Let us consider a set of given jobs as shown in the following table. We have to find a sequence of jobs, which will be completed within their deadlines and will give maximum profit. Each job is associated with a deadline and profit.

Solution

To solve this problem, the given jobs are sorted according to their profit in a descending order. Hence, after sorting, the jobs are ordered as shown in the following table.

From this set of jobs, first we select J2, as it can be completed within its deadline and contributes maximum profit.

• Next, J1 is selected as it gives more profit compared to J4.
• In the next clock, J4 cannot be selected as its deadline is over, hence J3 is selected as it executes within its deadline.
• The job J5 is discarded as it cannot be executed within its deadline.

Thus, the solution is the sequence of jobs (J2, J1, J3), which are being executed within their deadline and gives maximum profit.

Total profit of this sequence is 100 + 60 + 20 = 180.

Key takeaway

Algorithm: Job-Sequencing-With-Deadline (D, J, n, k)

D(0) := J(0) := 0

k := 1

J(1) := 1   // means first job is selected

for i = 2 … n do

   r := k

   while D(J(r)) > D(i) and D(J(r)) ≠ r do

      r := r – 1

   if D(J(r)) ≤ D(i) and D(i) > r then

      for l = k … r + 1 by -1 do

         J(l + 1) := J(l)

         J(r + 1) := i

         k := k + 1

3.9 Huffman Coding

• i) Data can be encoded efficiently using Huffman Codes.
• (ii) It is a widely used and beneficial technique for compressing data.
• (iii) Huffman's greedy algorithm uses a table of the frequencies of occurrences of each character to build up an optimal way of representing each character as a binary string.

Suppose we have 105 characters in a data file. Normal Storage: 8 bits per character (ASCII) - 8 x 105 bits in a file. But we want to compress the file and save it compactly. Suppose only six characters appear in the file:

How can we represent the data in a Compact way?

(i) Fixed length Code: Each letter represented by an equal number of bits. With a fixed length code, at least 3 bits per character:

For example:

a   000

b   001

c   010

d   011

e   100

f   101

For a file with 105 characters, we need 3 x 105 bits.

(ii) A variable-length code: It can do considerably better than a fixed-length code, by giving many characters short code words and infrequent character long codewords.

For example:

  a       0

  b      101

  c      100

  d      111

  e      1101

  f      1100

Number of bits = (45 x 1 + 13 x 3 + 12 x 3 + 16 x 3 + 9 x 4 + 5 x 4) x 1000

= 2.24 x 105bits

Thus, 224,000 bits to represent the file, a saving of approximately 25%.This is an optimal character code for this file.

Prefix Codes:

The prefixes of an encoding of one character must not be equal to complete encoding of another character, e.g., 1100 and 11001 are not valid codes because 1100 is a prefix of some other code word is called prefix codes.

Prefix codes are desirable because they clarify encoding and decoding. Encoding is always simple for any binary character code; we concatenate the code words describing each character of the file. Decoding is also quite comfortable with a prefix code. Since no codeword is a prefix of any other, the codeword that starts with an encoded data is unambiguous.

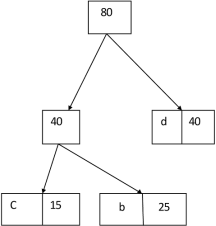
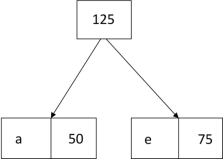
Greedy Algorithm for constructing a Huffman Code:

Huffman invented a greedy algorithm that creates an optimal prefix code called a Huffman Code.

Fig 7 – Greedy Algorithm for constructing a Huffman Code

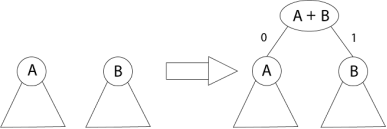
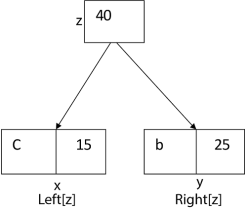
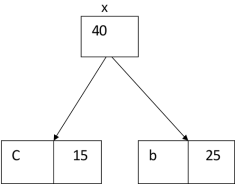
The algorithm builds the tree T analogous to the optimal code in a bottom-up manner. It starts with a set of |C| leaves (C is the number of characters) and performs |C| - 1 'merging' operations to create the final tree. In the Huffman algorithm 'n' denotes the quantity of a set of characters, z indicates the parent node, and x & y are the left & right child of z respectively.

Algorithm of Huffman Code

Huffman (C)

1. n=|C|

2. Q ← C

3. for i=1 to n-1

4. do

5. z= allocate-Node ()

6. x=  left[z]=Extract-Min(Q)

7. y= right[z] =Extract-Min(Q)

8. f [z]=f[x]+f[y]

9. Insert (Q, z)

10. return Extract-Min (Q)

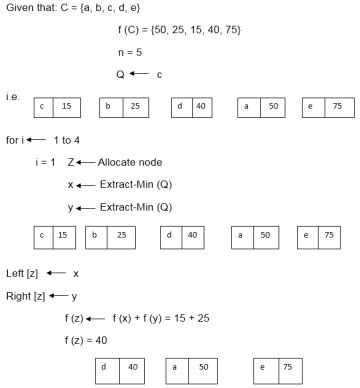
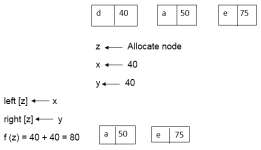
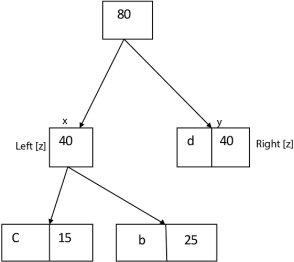
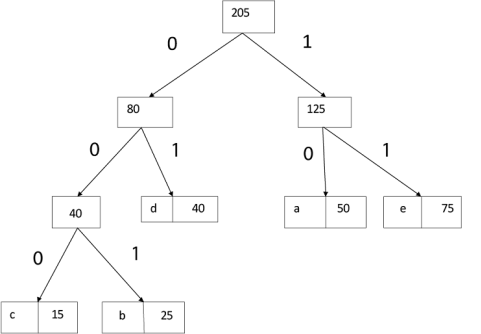
Example: Find an optimal Huffman Code for the following set of frequencies:

1. a: 50   b: 25   c: 15   d: 40   e: 75  

Solution:

i.e.

Key takeaway

• (i) Data can be encoded efficiently using Huffman Codes.
• (ii) It is a widely used and beneficial technique for compressing data.
• (iii) Huffman's greedy algorithm uses a table of the frequencies of occurrences of each character to build up an optimal way of representing each character as a binary string.

3.10 Single source shortest path problem

Introduction:

In a shortest- paths problem, we are given a weighted, directed graphs G = (V, E), with weight function w: E → R mapping edges to real-valued weights. The weight of path p = (v0,v1,..... vk) is the total of the weights of its constituent edges:

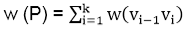
We define the shortest - path weight from u to v by δ(u,v) = min (w (p): u→v), if there is a path from u to v, and δ(u,v)= ∞, otherwise.

The shortest path from vertex s to vertex t is then defined as any path p with weight w (p) = δ(s,t).

The breadth-first- search algorithm is the shortest path algorithm that works on unweighted graphs, that is, graphs in which each edge can be considered to have unit weight.

In a Single Source Shortest Paths Problem, we are given a Graph G = (V, E), we want to find the shortest path from a given source vertex s ∈ V to every vertex v ∈ V.

Variants:

There are some variants of the shortest path problem.

• Single- destination shortest - paths problem: Find the shortest path to a given destination vertex t from every vertex v. By shift the direction of each edge in the graph, we can shorten this problem to a single - source problem.
• Single - pair shortest - path problem: Find the shortest path from u to v for given vertices u and v. If we determine the single - source problem with source vertex u, we clarify this problem also. Furthermore, no algorithms for this problem are known that run asymptotically faster than the best single - source algorithms in the worst case.
• All - pairs shortest - paths problem: Find the shortest path from u to v for every pair of vertices u and v. Running a single - source algorithm once from each vertex can clarify this problem; but it can generally be solved faster, and its structure is of interest in the own right.

Shortest Path: Existence:

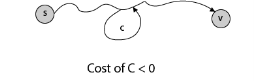
If some path from s to v contains a negative cost cycle then, there does not exist the shortest path. Otherwise, there exists a shortest s - v that is simple.

Fig 8 - Shortest Path: Existence

The single source shortest path algorithm (for arbitrary weight positive or negative) is also known Bellman-Ford algorithm is used to find minimum distance from source vertex to any other vertex. The main difference between this algorithm with Dijkstra’s algorithm is, in Dijkstra’s algorithm we cannot handle the negative weight, but here we can handle it easily.

Fig 9 - The single source shortest path algorithm

Bellman-Ford algorithm finds the distance in bottom up manner. At first it finds those distances which have only one edge in the path. After that increase the path length to find all possible solutions.

Input − The cost matrix of the graph:

0 6 ∞ 7 ∞

∞ 0 5 8 -4

∞ -2 0 ∞ ∞

∞ ∞ -3 0 9

2 ∞ 7 ∞ 0

Output − Source Vertex: 2
Vert: 0 1 2 3 4
Dist: -4 -2 0 3 -6
Pred: 4 2 -1 0 1
The graph has no negative edge cycle

Algorithm

Output

Source Vertex: 2

Vert: 0 1 2 3 4

Dist: -4 -2 0 3 -6

Pred: 4 2 -1 0 1

The graph has no negative edge cycle

Key takeaway

In a shortest- paths problem, we are given a weighted, directed graphs G = (V, E), with weight function w: E → R mapping edges to real-valued weights. The weight of path p = (v0,v1,..... vk) is the total of the weights of its constituent edges:

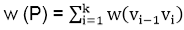
We define the shortest - path weight from u to v by δ(u,v) = min (w (p): u→v), if there is a path from u to v, and δ(u,v)= ∞, otherwise.

The shortest path from vertex s to vertex t is then defined as any path p with weight w (p) = δ(s,t).

The breadth-first- search algorithm is the shortest path algorithm that works on unweighted graphs, that is, graphs in which each edge can be considered to have unit weight.

In a Single Source Shortest Paths Problem, we are given a Graph G = (V, E), we want to find the shortest path from a given source vertex s ∈ V to every vertex v ∈ V.

3.11 Dynamic Programming

Dynamic programming approach is similar to divide and conquer in breaking down the problem into smaller and yet smaller possible sub-problems. But unlike, divide and conquer, these sub-problems are not solved independently. Rather, results of these smaller sub-problems are remembered and used for similar or overlapping sub-problems.

Dynamic programming is used where we have problems, which can be divided into similar sub-problems, so that their results can be re-used. Mostly, these algorithms are used for optimization. Before solving the in-hand sub-problem, dynamic algorithm will try to examine the results of the previously solved sub-problems. The solutions of sub-problems are combined in order to achieve the best solution.

So we can say that −

• The problem should be able to be divided into smaller overlapping sub-problem.
• An optimum solution can be achieved by using an optimum solution of smaller sub-problems.
• Dynamic algorithms use Memoization.

Comparison

In contrast to greedy algorithms, where local optimization is addressed, dynamic algorithms are motivated for an overall optimization of the problem.

In contrast to divide and conquer algorithms, where solutions are combined to achieve an overall solution, dynamic algorithms use the output of a smaller sub-problem and then try to optimize a bigger sub-problem. Dynamic algorithms use Memoization to remember the output of already solved sub-problems.

Example

The following computer problems can be solved using dynamic programming approach −

• Fibonacci number series
• Knapsack problem
• Tower of Hanoi
• All pair shortest path by Floyd-Warshall
• Shortest path by Dijkstra
• Project scheduling

Dynamic programming can be used in both top-down and bottom-up manner. And of course, most of the times, referring to the previous solution output is cheaper than recomputing in terms of CPU cycles.

Key takeaway

Dynamic programming approach is similar to divide and conquer in breaking down the problem into smaller and yet smaller possible sub-problems. But unlike, divide and conquer, these sub-problems are not solved independently. Rather, results of these smaller sub-problems are remembered and used for similar or overlapping sub-problems.

Dynamic programming is used where we have problems, which can be divided into similar sub-problems, so that their results can be re-used. Mostly, these algorithms are used for optimization. Before solving the in-hand sub-problem, dynamic algorithm will try to examine the results of the previously solved sub-problems. The solutions of sub-problems are combined in order to achieve the best solution.

3.12 Difference between dynamic programming and divide and conquer

Key takeaway

3.13 Applications: Fibonacci Series, Matrix Chain Multiplication, 0-1 Knapsack Problem, Longest Common Subsequence, Travelling Salesman Problem, Rod Cutting, Bin Packing

Fibonacci sequence

Fibonacci sequence is the sequence of numbers in which every next item is the total of the previous two items. And each number of the Fibonacci sequence is called Fibonacci number.

Example: 0 ,1,1,2,3,5,8,13,21,....................... is a Fibonacci sequence.

The Fibonacci numbers F_nare defined as follows:

F0 = 0

Fn=1

Fn=F(n-1)+ F(n-2)

FIB (n)

 1. If (n < 2)

 2. then return n

 3. else return FIB (n - 1) + FIB (n - 2)

Figure 10 : shows four levels of recursion for the call fib (8):

Figure: Recursive calls during computation of Fibonacci number

A single recursive call to fib (n) results in one recursive call to fib (n - 1), two recursive calls to fib (n - 2), three recursive calls to fib (n - 3), five recursive calls to fib (n - 4) and, in general, Fk-1 recursive calls to fib (n - k) We can avoid this unneeded repetition by writing down the conclusion of recursive calls and looking them up again if we need them later. This process is called memorization.

Here is the algorithm with memorization

MEMOFIB (n)

 1 if (n < 2)

 2 then return n

 3 if (F[n] is undefined)

 4 then F[n] ← MEMOFIB (n - 1) + MEMOFIB (n - 2)

 5 return F[n]

If we trace through the recursive calls to MEMOFIB, we find that array F [] gets filled from bottom up. I.e., first F [2], then F [3], and so on, up to F[n]. We can replace recursion with a simple for-loop that just fills up the array F [] in that order

ITERFIB (n)

 1 F [0] ← 0

 2 F [1] ← 1

 3 for i ← 2 to n

 4 do

 5 F[i] ← F [i - 1] + F [i - 2]

 6 return F[n]

This algorithm clearly takes only O (n) time to compute Fn. By contrast, the original recursive algorithm takes O (∅n;),∅ = 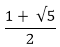= 1.618. ITERFIB conclude an exponential speedup over the original recursive algorithm.

Matrix Chain Multiplication

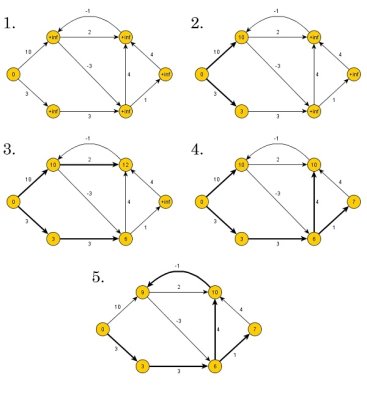
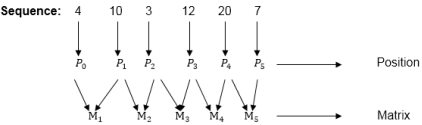
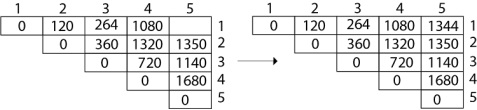
Example: We are given the sequence {4, 10, 3, 12, 20, and 7}. The matrices have size 4 x 10, 10 x 3, 3 x 12, 12 x 20, 20 x 7. We need to compute M [i,j], 0 ≤ i, j≤ 5. We know M [i, i] = 0 for all i.

Let us proceed with working away from the diagonal. We compute the optimal solution for the product of 2 matrices.

Here P0 to P5 are Position and M1 to M5 are matrix of size (pi to pi-1)

On the basis of sequence, we make a formula

In Dynamic Programming, initialization of every method done by '0'.So we initialize it by '0'.It will sort out diagonally.

We have to sort out all the combination but the minimum output combination is taken into consideration.

Calculation of Product of 2 matrices:

1. m (1,2) = m1  x m2

           = 4 x 10 x  10 x 3

           = 4 x 10 x 3 = 120

2. m (2, 3) = m2 x m3

            = 10 x 3  x  3 x 12

            = 10 x 3 x 12 = 360

3. m (3, 4) = m3 x m4

            = 3 x 12  x  12 x 20

            = 3 x 12 x 20 = 720

4. m (4,5) = m4 x m5

           = 12 x 20  x  20 x 7

           = 12 x 20 x 7 = 1680

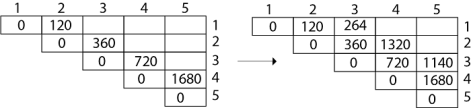
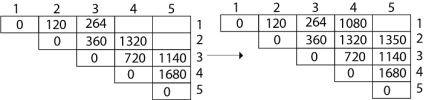
• We initialize the diagonal element with equal i,j value with '0'.
• After that second diagonal is sorted out and we get all the values corresponded to it

Now the third diagonal will be solved out in the same way.

Now product of 3 matrices:

M [1, 3] = M1 M2 M3

1. There are two cases by which we can solve this multiplication: ( M1 x M2) + M3, M1+ (M2x M3)
2. After solving both cases we choose the case in which minimum output is there.

M [1, 3] =264

As Comparing both output 264 is minimum in both cases so we insert 264 in table and ( M1 x M2) + M3 this combination is chosen for the output making.

M [2, 4] = M2 M3 M4

1. There are two cases by which we can solve this multiplication: (M2x M3)+M4, M2+(M3 x M4)
2. After solving both cases we choose the case in which minimum output is there.

M [2, 4] = 1320

As Comparing both output 1320 is minimum in both cases so we insert 1320 in table and M2+(M3 x M4) this combination is chosen for the output making.

M [3, 5] = M3  M4  M5

1. There are two cases by which we can solve this multiplication: ( M3 x M4) + M5, M3+ ( M4xM5)
2. After solving both cases we choose the case in which minimum output is there.

M [3, 5] = 1140

As Comparing both output 1140 is minimum in both cases so we insert 1140 in table and ( M3 x M4) + M5this combination is chosen for the output making.

Now Product of 4 matrices:

M [1, 4] = M1  M2 M3 M4

There are three cases by which we can solve this multiplication:

1. ( M1 x M2 x M3) M4
2. M1 x(M2 x M3 x M4)
3. (M1 xM2) x ( M3 x M4)

After solving these cases we choose the case in which minimum output is there

M [1, 4] =1080

As comparing the output of different cases then '1080' is minimum output, so we insert 1080 in the table and (M1 xM2) x (M3 x M4) combination is taken out in output making,

M [2, 5] = M2 M3 M4 M5

There are three cases by which we can solve this multiplication:

1. (M2 x M3 x M4)x M5
2. M2 x( M3 x M4 x M5)
3. (M2 x M3)x ( M4 x M5)

After solving these cases we choose the case in which minimum output is there

M [2, 5] = 1350

As comparing the output of different cases then '1350' is minimum output, so we insert 1350 in the table and M2 x( M3 x M4 xM5)combination is taken out in output making.

Now Product of 5 matrices:

M [1, 5] = M1  M2 M3 M4 M5

There are five cases by which we can solve this multiplication:

1. (M1 x M2 xM3 x M4 )x M5
2. M1 x( M2 xM3 x M4 xM5)
3. (M1 x M2 xM3)x M4 xM5
4. M1 x M2x(M3 x M4 xM5)

After solving these cases we choose the case in which minimum output is there

M [1, 5] = 1344

As comparing the output of different cases then '1344' is minimum output, so we insert 1344 in the table and M1 x M2 x(M3 x M4 x M5)combination is taken out in output making.

Final Output is:

Step 3: Computing Optimal Costs: let us assume that matrix Ai has dimension pi-1x pi for i=1, 2, 3....n. The input is a sequence (p0,p1,......pn) where length [p] = n+1. The procedure uses an auxiliary table m [1....n, 1.....n] for storing m [i, j] costs an auxiliary table s [1.....n, 1.....n] that record which index of k achieved the optimal costs in computing m [i, j].

The algorithm first computes m [i, j] ← 0 for i=1, 2, 3.....n, the minimum costs for the chain of length 1.

Algorithm of Matrix Chain Multiplication

MATRIX-CHAIN-ORDER (p)

 1. n   length[p]-1

 2. for i ← 1 to n

 3. do m [i, i] ← 0

 4. for l ← 2 to n    // l is the chain length

 5. do for i ← 1 to n-l + 1

 6. do j ← i+ l -1

 7. m[i,j] ←  ∞

 8. for k  ← i to j-1

 9. do q  ← m [i, k] + m [k + 1, j] + pi-1 pk pj 

 10. If q < m [i,j]

 11. then m [i,j] ← q

 12. s [i,j] ← k

 13. return m and s.     

We will use table s to construct an optimal solution.

Step 1: Constructing an Optimal Solution:

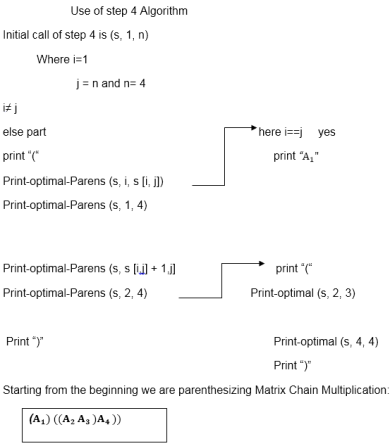
PRINT-OPTIMAL-PARENS (s, i, j)

 1. if i=j

 2. then print "A"

 3. else print "("

 4. PRINT-OPTIMAL-PARENS (s, i, s [i, j])

 5. PRINT-OPTIMAL-PARENS (s, s [i, j] + 1, j)

 6. print ")"

Analysis: There are three nested loops. Each loop executes a maximum n times.

1. l, length, O (n) iterations.
2. i, start, O (n) iterations.
3. k, split point, O (n) iterations

Body of loop constant complexity

Total Complexity is: O (n3)

Algorithm with Explained Example

Question: P [7, 1, 5, 4, 2}

Solution: Here, P is the array of a dimension of matrices.

So here we will have 4 matrices:

A17x1  A21x5  A35x4  A44x2

i.e.

First Matrix A1 have dimension 7 x 1

Second Matrix A2 have dimension 1 x 5

Third Matrix A3 have dimension 5 x 4

Fourth Matrix A4 have dimension 4 x 2

Let say,

From P = {7, 1, 5, 4, 2} - (Given)

And P is the Position

p0 = 7, p1 =1, p2 = 5, p3 = 4, p4=2.

Length of array P = number of elements in P

∴length (p)= 5

From step 3

Follow the steps in Algorithm in Sequence

According to Step 1 of Algorithm Matrix-Chain-Order

Step 1:

 n ← length [p]-1

    Where n is the total number of elements

     And length [p] = 5

∴ n = 5 - 1 = 4

n = 4

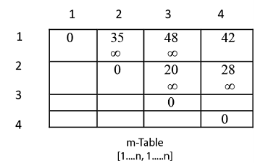
Now we construct two tables m and s.

Table m has dimension [1.....n, 1.......n]

Table s has dimension [1.....n-1, 2.......n]

Now, according to step 2 of Algorithm

1. for i ← 1 to n  
2. this means: for i ← 1 to 4 (because n =4)  
3. for  i=1  
4. m [i, i]=0  
5. m [1, 1]=0  
6. Similarly for i = 2, 3, 4  
7. m [2, 2] = m [3,3] = m [4,4] = 0  
8. i.e. fill all the diagonal entries "0" in the table m  
9. Now,  
10. l ← 2 to n  
11. l ← 2 to 4    (because n =4 )  

Case 1:

1. When l - 2

    for (i ← 1 to n - l + 1)

     i ← 1 to 4 - 2 + 1

     i ← 1 to 3

When i = 1

  do   j ← i + l - 1

          j ← 1 + 2 - 1

          j ← 2

     i.e. j = 2

Now, m [i, j] ← ∞ 

 i.e. m [1,2] ← ∞

Put ∞ in m [1, 2] table

   for k ← i to j-1

        k ← 1 to 2 - 1

        k ← 1 to 1

            k = 1

Now q ← m [i, k] + m [k + 1, j] + pi-1 pk pj

   for l = 2

        i = 1

        j =2

       k = 1

     q ← m [1,1] + m [2,2] + p0x p1x p2

             and m [1,1] = 0

    for i ← 1 to 4

     ∴ q ← 0 + 0 + 7 x 1 x 5

     q ← 35

We have m [i, j] = m [1, 2] = ∞

Comparing q with m [1, 2]

  q < m [i, j]

  i.e. 35 < m [1, 2]

  35 < ∞

  True

 then, m [1, 2 ] ← 35  (∴ m [i,j] ← q)

  s [1, 2] ← k

 and the value of k = 1

  s [1,2 ] ← 1

Insert "1" at dimension s [1, 2] in table s. And 35 at m [1, 2]

2. l remains 2

    L = 2

      i ← 1 to n - l + 1

      i ← 1 to 4 - 2 + 1

      i ← 1 to 3

  for i = 1 done before

  Now value of i becomes 2

  i = 2

j ←  i + l - 1

   j ←  2 + 2 - 1

   j ←  3

  j = 3

m [i , j]  ← ∞

i.e. m [2,3] ← ∞

 Initially insert ∞ at m [2, 3]

Now, for k ← i to j - 1

  k ← 2 to 3 - 1

  k ← 2 to 2

  i.e. k =2

  Now, q ← m [i, k] + m [k + 1, j] + pi-1 pk pj

  For l =2

        i = 2

        j = 3

        k = 2

  q ← m [2, 2] + m [3, 3] + p1x p2 x p3

                q ← 0 + 0 + 1 x 5 x 4

       q ← 20

       Compare q with m [i ,j ]

  If q < m [i,j]

 i.e. 20 < m [2, 3]

20 < ∞       

True

Then m [i,j ] ← q

      m [2, 3 ] ← 20

and s [2, 3] ← k

 and k = 2

s [2,3] ← 2

3. Now i become 3

  i = 3

  l = 2

j ← i + l - 1

j ← 3 + 2 - 1

j ← 4

j = 4

Now, m [i, j ] ← ∞

          m [3,4 ] ← ∞

Insert ∞ at m [3, 4]

  for k ← i to j - 1

        k ← 3 to 4 - 1

        k ← 3 to 3

 i.e. k = 3

Now, q ← m [i, k] + m [k + 1, j] + pi-1 pk pj

i = 3

    l = 2

    j = 4

    k = 3

q ← m [3, 3] + m [4,4] + p2  x p3 x p4

q ← 0 + 0 + 5 x 2 x 4

q   40

Compare q with m [i, j]

  If q < m [i, j]

     40 < m [3, 4]

     40 < ∞

  True

Then, m [i,j] ← q

       m [3,4] ← 40

and s [3,4] ← k

   s [3,4] ← 3

Case 2: l becomes 3

      L = 3

       for i = 1 to n - l + 1

            i = 1 to 4 - 3 + 1

   i = 1 to 2

When i = 1

 j ← i + l - 1

 j ← 1 + 3 - 1

         j ← 3

 j = 3

Now, m [i,j]   ← ∞

          m [1, 3]  ←  ∞

for k ← i to j - 1

     k ← 1 to 3 - 1

     k ← 1 to 2

Now we compare the value for both k=1 and k = 2. The minimum of two will be placed in m [i,j] or s [i,j] respectively.

Now from above

Value of q become minimum for k=1   

  ∴ m [i,j] ← q

      m [1,3] ← 48

Also m [i,j] > q

i.e. 48 < ∞

∴ m [i , j] ← q

   m [i, j] ← 48

and s [i,j] ← k

i.e. m [1,3] ← 48

   s [1, 3] ←  1

Now i become 2

 i = 2

  l = 3

then j ← i + l -1

    j ←  2 + 3 - 1

    j ← 4

    j = 4 

    so m [i,j] ← ∞

m [2,4] ← ∞

Insert initially ∞ at m [2, 4]

      for k   ← i to j-1

       k  ← 2 to 4 - 1

       k  ← 2 to 3

Here, also find the minimum value of m [i,j] for two values of k = 2 and k =3

1. But 28 <     ∞  
2.  So m [i,j] ← q  
3.     And q  ← 28  
4. m [2, 4]  ← 28  
5. and   s [2, 4]  ← 3  
6. e. It means in s table at s [2,4] insert 3 and at m [2,4] insert 28.  

Case 3: l becomes 4

L = 4

    For i ← 1 to n-l + 1

  i ← 1 to 4 - 4 + 1

  i ← 1

  i = 1

 do j  ← i + l - 1

      j ← 1 + 4 - 1

      j ← 4

     j = 4

Now m [i,j]  ←  ∞

        m [1,4] ←  ∞

for k  ← i to j -1

     k ← 1 to 4 - 1

     k  ← 1 to 3

When k = 1

q  ←  m [i, k] + m [k + 1, j] + pi-1 pk pj               

q  ← m [1,1] + m [2,4] + p0xp4x p1

q ← 0 + 28 + 7 x 2 x 1

q  ← 42

Compare q and m [i, j]

m [i,j] was ∞

i.e. m [1,4]

if q < m [1,4]

   42< ∞

    True

Then m [i,j] ← q

 m [1,4] ← 42

and s [1,4]  1 ? k =1

When k = 2

 L = 4, i=1, j = 4

q ← m [i, k] + m [k + 1, j] + pi-1 pk pj               

q ← m [1, 2] + m [3,4] + p0 xp2 xp4

q ← 35 + 40 + 7 x 5 x 2

q  ← 145

Compare q and m [i,j]

Now m [i, j]

      i.e. m [1,4] contains 42.

So if q < m [1, 4]

But 145 less than or not equal to m [1, 4]

   So 145 less than or not equal to 42.

So no change occurs.

When k = 3

 l = 4

 i = 1

 j = 4

q  ←  m [i, k] + m [k + 1, j] + pi-1 pk pj               

q ← m [1, 3] + m [4,4] + p0 xp3 x p4

q ← 48 + 0 + 7 x 4 x 2

q  ← 114

Again q less than or not equal to m [i, j]

 i.e. 114 less than or not equal to m [1, 4]

        114 less than or not equal to 42

So no change occurs. So the value of m [1, 4] remains 42. And value of s [1, 4] = 1

Now we will make use of only s table to get an optimal solution.

Longest Common Sequence (LCS)

A subsequence of a given sequence is just the given sequence with some elements left out.

Given two sequences X and Y, we say that the sequence Z is a common sequence of X and Y if Z is a subsequence of both X and Y.

In the longest common subsequence problem, we are given two sequences X = (x1 x2....xm) and Y = (y1 y2 yn) and wish to find a maximum length common subsequence of X and Y. LCS Problem can be solved using dynamic programming.

Characteristics of Longest Common Sequence

A brute-force approach we find all the subsequences of X and check each subsequence to see if it is also a subsequence of Y, this approach requires exponential time making it impractical for the long sequence.

Given a sequence X = (x1 x2.....xm) we define the ith prefix of X for i=0, 1, and 2...m as Xi= (x1 x2.....xi). For example: if X = (A, B, C, B, C, A, B, C) then X4= (A, B, C, B)

Optimal Substructure of an LCS: Let X = (x1 x2....xm) and Y = (y1 y2.....) yn) be the sequences and let Z = (z1 z2......zk) be any LCS of X and Y.

• If xm = yn, then zk=x_m=yn and Zk-1 is an LCS of Xm-1and Yn-1
• If xm ≠ yn, then zk≠ xm implies that Z is an LCS of Xm-1and Y.
• If xm ≠ yn, then zk≠yn implies that Z is an LCS of X and Yn-1

Step 2: Recursive Solution: LCS has overlapping subproblems property because to find LCS of X and Y, we may need to find the LCS of Xm-1 and Yn-1. If xm ≠ yn, then we must solve two subproblems finding an LCS of X and Yn-1.Whenever of these LCS's longer is an LCS of x and y. But each of these subproblems has the subproblems of finding the LCS of Xm-1 and Yn-1.

Let c [i,j] be the length of LCS of the sequence Xiand Yj.If either i=0 and j =0, one of the sequences has length 0, so the LCS has length 0. The optimal substructure of the LCS problem given the recurrence formula

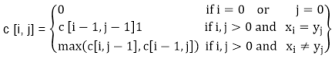
Step3: Computing the length of an LCS: let two sequences X = (x1 x2.....xm) and Y = (y1 y2..... yn) as inputs. It stores the c [i,j] values in the table c [0......m,0..........n].Table b [1..........m, 1..........n] is maintained which help us to construct an optimal solution. c [m, n] contains the length of an LCS of X,Y.

Algorithm of Longest Common Sequence

LCS-LENGTH (X, Y)

 1. m ← length [X]          

 2. n ← length [Y]

 3. for i ← 1 to m

 4. do c [i,0] ← 0

 5. for j ← 0 to m

 6. do c [0,j] ← 0

 7. for i ← 1 to m

 8. do for j ← 1 to n

 9. do if xi= yj 

 10. then c [i,j] ← c [i-1,j-1] + 1 

 11. b [i,j] ← "↖"

 12. else if c[i-1,j] ≥ c[i,j-1]

 13. then c [i,j] ← c [i-1,j]

 14. b [i,j] ← "↑"

 15. else c [i,j] ← c [i,j-1]

 16. b [i,j] ← "← "

 17. return c and b.

Example of Longest Common Sequence

Example: Given two sequences X [1...m] and Y [1.....n]. Find the longest common subsequences to both.

here X = (A,B,C,B,D,A,B) and Y = (B,D,C,A,B,A)

     m = length [X] and n = length [Y]

     m = 7 and n = 6

Here x1= x [1] = A   y1= y [1] = B

     x2= B  y2= D 

     x3= C  y3= C

     x4= B  y4= A

     x5= D  y5= B

     x6= A  y6= A

     x7= B

Now fill the values of c [i, j] in m x n table

Initially, for i=1 to 7 c [i, 0] = 0

          For j = 0 to 6 c [0, j] = 0

That is:

Now for i=1 and j = 1

 x1 and y1 we get x1 ≠ y1 i.e. A ≠ B

And  c [i-1,j] = c [0, 1] = 0

 c [i, j-1] = c [1,0 ] = 0

That is, c [i-1,j]= c [i, j-1] so c [1, 1] = 0 and b [1, 1] = ' ↑  '

Now for i=1 and j = 2

x1 and y2 we get x1 ≠ y2 i.e. A ≠ D

 c [i-1,j] = c [0, 2] = 0

 c [i, j-1] = c [1,1 ] = 0

That is, c [i-1,j]= c [i, j-1] and c [1, 2] = 0 b [1, 2] = '  ↑  '

Now for i=1 and j = 3

 x1 and y3 we get x1 ≠ y3 i.e. A ≠ C

 c [i-1,j] = c [0, 3] = 0

 c [i, j-1] = c [1,2 ] = 0

so c [1,3] = 0     b [1,3] = ' ↑ '

Now for i=1 and j = 4

 x1 and y4 we get. x1=y4 i.e A = A

  c [1,4] = c [1-1,4-1] + 1

     = c [0, 3] + 1

      = 0 + 1 = 1

 c [1,4] = 1

 b [1,4] = '  ↖  '

Now for i=1 and j = 5

           x1 and y5  we get x1 ≠ y5

           c [i-1,j] = c [0, 5] = 0

 c [i, j-1] = c [1,4 ] = 1

Thus c [i, j-1] >  c [i-1,j] i.e. c [1, 5] = c [i, j-1] = 1. So b [1, 5] = '←'

Now for i=1 and j = 6

           x1 and y6   we get x1=y6

                     c [1, 6] = c [1-1,6-1] + 1

                              = c [0, 5] + 1 = 0 + 1 = 1

     c [1,6] = 1

     b [1,6] = '  ↖  '

Now for i=2 and j = 1

 We get x2 and y1 B = B i.e.  x2= y1

             c [2,1] = c [2-1,1-1] + 1

                     = c [1, 0] + 1

                     = 0 + 1 = 1  

             c [2, 1] = 1 and b [2, 1] = ' ↖ '

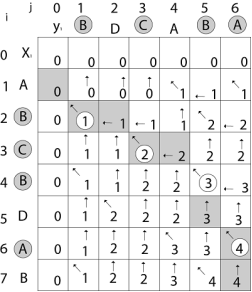
Similarly, we fill the all values of c [i, j] and we get

Step 4: Constructing an LCS: The initial call is PRINT-LCS (b, X, X.length, Y.length)

PRINT-LCS (b, x, i, j)

 1. if i=0 or j=0

 2. then return

 3. if b [i,j] = ' ↖ '

 4. then PRINT-LCS (b,x,i-1,j-1)

 5. print x_i

 6. else if b [i,j] = '  ↑  '

 7. then PRINT-LCS (b,X,i-1,j)

 8. else PRINT-LCS (b,X,i,j-1)

Example: Determine the LCS of (1,0,0,1,0,1,0,1) and (0,1,0,1,1,0,1,1,0).

Solution: let X = (1,0,0,1,0,1,0,1) and Y = (0,1,0,1,1,0,1,1,0).

We are looking for c [8, 9]. The following table is built.

From the table we can deduct that LCS = 6. There are several such sequences, for instance (1,0,0,1,1,0) (0,1,0,1,0,1) and (0,0,1,1,0,1)

Knapsack Problem:

Knapsack is basically means bag. A bag of given capacity.

We want to pack n items in your luggage.

• The ith item is worth vi dollars and weight wi pounds.
• Take as valuable a load as possible, but cannot exceed W pounds.
• vi wi W are integers.

1. W ≤ capacity  
2. Value ← Max  

Input:

• Knapsack of capacity
• List (Array) of weight and their corresponding value.

Output: To maximize profit and minimize weight in capacity.

The knapsack problem where we have to pack the knapsack with maximum value in such a manner that the total weight of the items should not be greater than the capacity of the knapsack.

Knapsack problem can be further divided into two parts:

1. Fractional Knapsack: Fractional knapsack problem can be solved by Greedy Strategy where as 0 /1 problem is not.

It cannot be solved by Dynamic Programming Approach.

0/1 Knapsack Problem:

In this item cannot be broken which means thief should take the item as a whole or should leave it. That's why it is called 0/1 knapsack Problem.

• Each item is taken or not taken.
• Cannot take a fractional amount of an item taken or take an item more than once.
• It cannot be solved by the Greedy Approach because it is enable to fill the knapsack to capacity.
• Greedy Approach doesn't ensure an Optimal Solution.

Example of 0/1 Knapsack Problem:

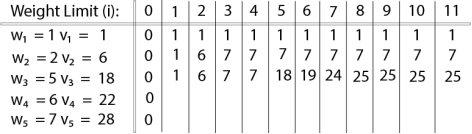
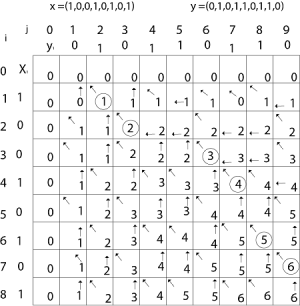
Example: The maximum weight the knapsack can hold is W is 11. There are five items to choose from. Their weights and values are presented in the following table:

The [i, j] entry here will be V [i, j], the best value obtainable using the first "i" rows of items if the maximum capacity were j. We begin by initialization and first row.

V [i, j] = max {V [i - 1, j], vi + V [i - 1, j -wi]

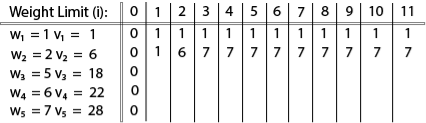
The value of V [3, 7] was computed as follows:

V [3, 7] = max {V [3 - 1, 7], v3 + V [3 - 1, 7 - w3]

         = max {V [2, 7], 18 + V [2, 7 - 5]}

         = max {7, 18 + 6}

         = 24

Finally, the output is:

The maximum value of items in the knapsack is 40, the bottom-right entry). The dynamic programming approach can now be coded as the following algorithm:

Algorithm of Knapsack Problem

KNAPSACK (n, W)

 1. for w = 0, W

 2. do V [0,w] ← 0

 3. for i=0, n

 4. do V [i, 0] ← 0 

 5. for w = 0, W

 6. do if (wi≤ w & vi + V [i-1, w -  wi]> V [i -1,W])

 7. then V [i, W] ← vi + V [i - 1, w - wi]

 8. else V [i, W] ← V [i - 1, w]

Traveling-salesman Problem

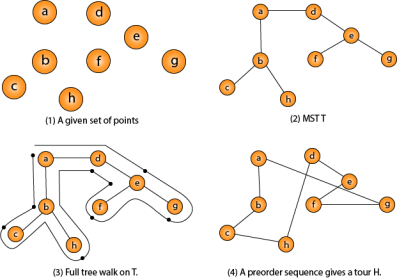
In the traveling salesman Problem, a salesman must visits n cities. We can say that salesman wishes to make a tour or Hamiltonian cycle, visiting each city exactly once and finishing at the city he starts from. There is a non-negative cost c (i, j) to travel from the city i to city j. The goal is to find a tour of minimum cost. We assume that every two cities are connected. Such problems are called Traveling-salesman problem (TSP).

We can model the cities as a complete graph of n vertices, where each vertex represents a city.

It can be shown that TSP is NPC.

If we assume the cost function c satisfies the triangle inequality, then we can use the following approximate algorithm.

Triangle inequality

Let u, v, w be any three vertices, we have

One important observation to develop an approximate solution is if we remove an edge from H*, the tour becomes a spanning tree.

1. Approx-TSP (G= (V, E))   
2. {  
3.   1. Compute a MST T of G;  
4.   2. Select any vertex r is the root of the tree;  
5.   3. Let L be the list of vertices visited in a preorder tree walk of T;  
6.   4. Return the Hamiltonian cycle H that visits the vertices in the order L;  
7. }