Module 2

Mathematical induction

Mathematical induction

Mathematical Induction is used to prove that each statement in a list of statement is true.

The list is countable infinite.

2.1 Principle of mathematical Induction

If: -

1)     When is statement is true for a natural number n=K , then it will also be true for its successor n=K+1

2)     The statement is true for n=1, then the statement will be true for every natural number n.

Que1. Prove that the sum of the first n natural numbers is given

1+2+3+…+n=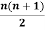

Sol. Step 1:-  Put n=K

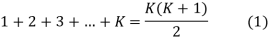
Step 2:- Put n= K+1

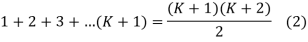
Add (K+1) terms to put side of equation 1

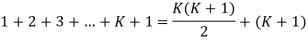
Now equation 1 and 3 are equal

Now put n=1 we have equation 1

Que2. The sum of consecutive cubes is equal to the square of the sum of first “n numbers.”

Sol.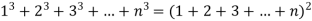

Step 1:- put n=K

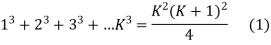
Step 2: Put n= K +1

Step 3: Add 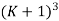to both sides of equation

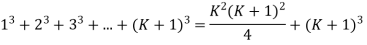
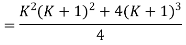
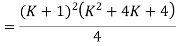
So equation 1 and 3 are equal

Now put n=1 in equation 1

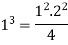
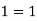
The formula is true for every natural number.

Theorem 1 :- Sum of a geometric sequence for any real number r except one and any integer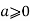

Proof:- Suppose r is a particular but arbitrarily chosen real number that is not equal to 1 and let the property 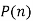be the equation.

We must shown that is true for all integers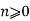

By mathematical induction on n show that P(0) is true

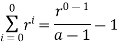
Also because r' = r and r+1 .

Hence P(0) is true.

Theorem 2 :- Show that all integers K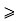 0 if P(K) is true then P(K+1) is also true.

Proof:- Let K be any integer with K 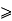0

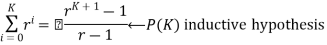
We must show that P(K+1) is true i.e.

Or equivalently that

We will show that left hand rule of P(K+1) equals the right hand side.

The left-hand rule of P(K+1) is

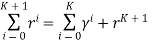
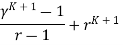
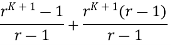
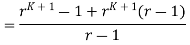
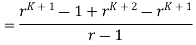
By multiplying out and using the fact that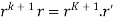

2.1.1 Strong mathematical induction

This is the technique for establishing the truth of a sequence of statement about integers.

Approved by strong mathematical Induction consists of a basic steps and an inductive step.

Basic step :- It may P contain proofs for several initial values.

Inductive step:- The truth of predicate P(n) is assumed not just for one value of n but for all values through K, and then truth of P(K+1) is proved.

Principle of strong mathematical induction

Let P(n) be a property that is defined for integers n, let ‘a' and 'b' be fixed integers with a b

1)     P(a), P(a+1)…P(b) are all true (basic step)

2)     For any integers K 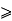b; if P(i) is true for all integers i from 'a' through K then P(K+1) is true. (Inductive step)

Theorem :- Existence and uniqueness of binary integer representation

Given any positive integer n, n has a unique representation in the form

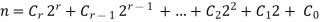
Where r is a non negative integer, 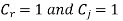or 0 for all j=0,1,2…r-1

Proof:- Let r=0, and 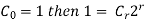and so n=1 can be written in in equation form.

Show that for all integers K 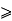1 if P(1) is true for all integers i from 1 through K then P(K+1) is also true.

Let K be an integer with K 1

Where r is a non negative integer 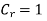and y=1 or '0' for all j=0,1,2,…r – 1

Case 1:- (K+1) is even.

In this case is an integer and by inductive hypothesis since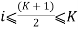

Then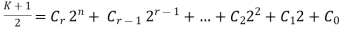

Where r is a non negative integer.

or 0 for all j=0,1,2,…r-1

Multiplying both sides of equation by 2 gives

K+1 =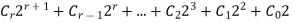

Which gives a sum of power of 2.

Case 2:- (K+1) is odd.

In this case is an integer and by induction hypothesis since then,

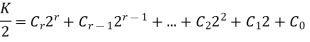
Multiplying both side of equation by 2 and add 1

Which is also sum of power of 2 of required form.

Que. Prove that any positive integer n>1 can be written as a product of primes using strong mathematical induction.

Proof:- P(n) be the statement. Every positive integer n>1 can be written as a product of primes.

Let n=2 and 2=2 (because 2 is itself prime)

P(2) is true.

Let us assume that assertion hold for n=K+1.

i.e. to prove that n=K+1 written as a product of primes.

Therefore there are two cases.

Case i) (K+1) is prime

Therefore (K+1) = (K+1) [because K + 1 is prime]

Therefore P(K+1) is true in this case.

Case ii) (K+1) is a complete number

(K+1) = l. m               (l, m )(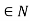

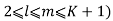
By induction assumption on integer l and m can be written as a product of primes l, m <K

P(l), P(m) is true.

Therefore (K+1) = (prime factors of l) × (prime factor of m)

= Product of primes

Therefore (K+1) is written as a product of primes.

P(K+1) is true in this case.

By case (i) and case (ii) P(K+1) is true. Therefore by strong mathematical Induction result is true for all positive integers.

2.2 Well ordering principle for the integers

Let S be a set of integers containing one or more integers all of which are greater than some fixed integers. Then S has a least element.

Theorem :- use mathematical induction to prove well ordering principle of integers.

Proof :- Let P(n) be the statement “Any non empty subset of integers having n number of elements has the least element.”

1)     P(1) is true because any subset of positive integers N, having just one element obviously has the least element.

2)     Assume that, for any m, every subset of N having K elements, K < m has the least elements.

3)     We will now prove that any subset of N having m elements has the least element.

Let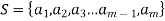

Where 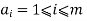are positive integer.

Consider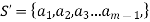

Then S' is a subset of N having (m-1) elements.

Since (m-1) < m, defer applying induction hypothesis to S', we know that S' has least element say 1.

Then min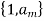 is the least element of S.

Thus, we have proved that S also has the least element.

2.3 Question remainder theorem (Division Algo)

Given any integer n and any positive integer d, there exist unique integers q and r such that

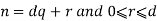
Proof:- Let S be the set of all non negative integers of the form

n- d K

Where K is an integer. This set has at least one element.

And so (n – 0.d) is in s and if n is negative then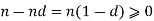

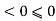
Since d is a positive integer and so (n – n d) is in S.

Some specific integers K=q

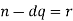
Adding dq to both sides gives

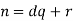
If r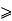 d then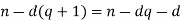

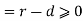
And so on 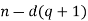would be non negative integer in S that would be smaller than r.

But r is the smaller integer in S. This contradiction shows that the superposition r 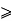d must be false.

The preceding arguments prove that there exist integer r and q for which

2.4 Euclidean theorem

The Euclidean algorithm is supposed to take integers A and B with A> B 0 and compute their greatest common divisor.

Precondition :- A and B are integers with A>B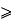 0. a=A, b=B and r=B.

While ( b≠0)

1)     r = a mod b

2)     a : =b

3)     b : r

End while

Post condition:- a = gcd (A,B)

Proof:- To prove the correctness of the loop, let the invariant be

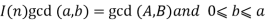
The good of while loop is

G : b≠0

1)     Basic property :- I(0) is true before the first iteration of the loop.

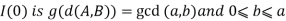
According to precondition

a = A, b = B, r = B ,  0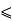 B A

Hence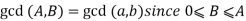

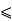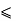b = B and a = A then 0 b a

Hence I(0) is true.

2.5 Inductive property

If 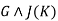  is true before and iteration of the loop then I (K+1) is true after iteration of the loop.

Since I(K) is true, immediately before statement I is executed.

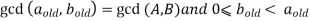
After execution of statement 1

And 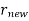has the property that

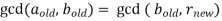
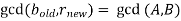
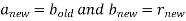
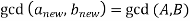and substituting the values from the equation

2.6 Recursive definitions of sums and products

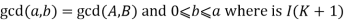
Given number of 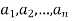where n is a positive integer the summation from i=1 to n of the denoted 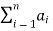is defined as follow

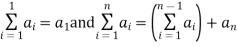
Thus product from i=1 to n of the 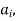 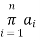 is defined as

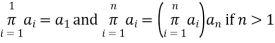
Que. Using interactive methods of the following recurrence relation

Given,

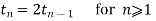
By interactive substitution we get

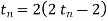
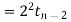
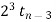
For i=n

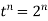
Is required solution.

Que. Solve the following recurrence relation 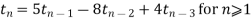subject to initial condition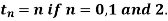

Sol. First let us assume the recurrence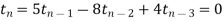

Characteristic polynomial is

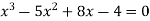
Roots are therefore 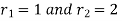with multiplicity 2, the general solution, therefore is

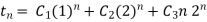
By initial conditions we get

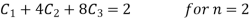
Solving these three equation we get

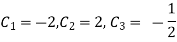
Solution is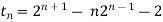

Que. Solve the following recurrence relation

Subject to initial condition

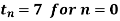
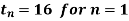
Let us write the recurrence

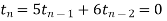
The characteristic polynomial is

Solving we get

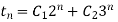
By initial condition we get

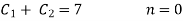
Solving we get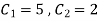

The solution is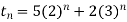

Que. Prove that n!+2 is divisible by 2 for all integers n 2.

Proof:- Let P(n) be (n! +2) is divisible by 2 for all integers n 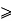2

i.e.  P(n) be 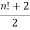is an integer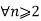 

Let n=2

n! +2 =2! +2 =4

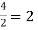= is an integer

P(2) is true.

Assume the result for n = K, i.e. 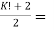m where m is an integer

Therefore K! + 2 = 2m

Now we have to prove that result for n = K+1

i.e. to prove 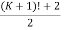is an integer

Consider,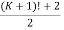

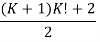
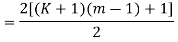
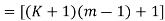
K, m is an integer.

(K+1)(m-1)+1 is also an integer.

is an integer.

P(K+1) is true.

By mathematical induction

(n! +2) is divisible by 2, for all integers n 2

Que. Prove that 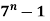divisible by 6, for each integer n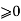

Proof:- Let P(n) be 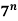-1 is divisible by 6,

i.e. P(n) : 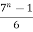is an integer,

Let n=0

P(0) = is an integer.

P(0) is true.

Let n=1

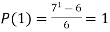is an integer.

P(1) is true

Assume that the result is true for n=K

i.e. 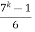is an integer.

i.e.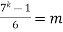

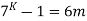
We have to prove that result from n= K +1

i.e to prove the result for

Consider

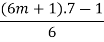
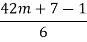
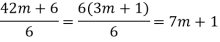
m is an integer

(7m + 1) is an integer.

P(K + 1) is true

Therefore by induction

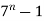is divisible by