Unit 4

Algebraic structure and morphism

4.1 Algebraic Set: --

Let S for a non-empty set. If S is associated with one or more binary operation. Then it’s called Algebraic structure.

It is denoted by (S=f1, t2 t3………tn)

General Properties of Addition

1) Associatively

(x +y ) + z = x + (y +z)

2) Commutative

x + y = y + x

3) Identity

X+ e1 = e1 + x = x ……e1=0

4) Inverse

x + (x) = e ………… (e =0)

Where e is identity.

4.2 General properties of multiplication.

1) Associative

(x ✴ 4) +2 = x ✴ (y✴ z)

2) Commutative

x✴ y = ( y✴ z)

3) Identity x✴ e2 = e2✴x =x ………..e2=1

4) Inverse x✴ x1 = e

5) Distributive

x  ✴ ( y +z ) = (x ✴y) + ( x ✴z)

x  + ( y z ) = (x ✴y) + ( x ✴z)

6) Cancellation property

x ✴ y = x ✴z     y = z

✴ 4.2aAlgebraic Structure  (s, ✴) of non empty set with a binary operation.

✴ 4.2bSemi Group An non empty set S together with binary & associative operation.

✴ 4.2cMonoid An non empty set Stogether with binary, associative operation & Identify.

✴ 4.2dGroup An non empty set together with binary, associative, Identity & Inverse is called group.

✴ 4.2eAbelian or Commentative Group  An non empty set S together with binary, associative Identity, Inverse & Commutative law.

✴ Key Points 1) Closure   Algebraic Structure

2) Closure + Associative   Sub group

3) Closure + Associative + Identity  Monoid 

4) Closure + Associative + Identity + Inverse  Group

5) Closure + Associative + Identity + Inverse

+ Commutative  Abelian

Q.1) Prove that set A = [0, 1, 2, 3, 4, 5} is finite Abelian group under mod 6

 We 1st prepare table of mode 6.

G – 2 1st column or the 1st row shows that 0 is the identify for +

G – 3 The position off 0 is the additive inverse in curry row show that every element of A has addition inverse eg. 1+ 5 = 0

Hence, inverse of 1 is 5 &inverse of 5 is 1. Also 3 + 3 = 0

2 + 4 = 0

G is group under addition modulo 6.

G4: Further a + b = b + a  eg 4 + 5 = 3

5 + 4 = 3

G is abelian group

Isomorphism, automorphism and homomorphism

4.3 Isomorphism:

Let (s,*) and (S’,*) be two semi group. A function f : S    S’ is called an isomorphism if s is one to one and onto and if

f(a+b)=f(a)*f(b). For all a,b in S

Procedure to find the isomorphism

Step 1: we dein the function f: S S’ with domain of f=S

Step 2: We shall show that f is one to one.

Step 3: We shall show that f is onto.

Step 4: We shall show that f(a*b)= f(a)*’ f(b).

Q1. Let S be the set of all even integers. Show that the smi groups (Z,+) and (S,+) are isomorphic

Step 1: we define thw function f: Z  S where f(a)=2a

Step 2: suppose f(a1) =f(a2). Then 2a1=2a2. Hence f is one to one

Step 3: Suppose b is an even integer. Then a=b/2 € Z and f(a)= f(b/2) = 2(b/2)=b. Hence fits onto.

Step 4: We have f (a+b)= 2(a+b)= 2a+2b= f(a)+f(b)

Hence (Z,+) and (S,+) are isomorphic.

4.4 Automorphism:

An isomorphism from a semi group (S,*) to (S,*) itself is called an automorphism (auto=self)on (S,*)

4.5 Homomorphism:

Let (S,*) and (S’,*) be two semi groups. A function f SS’ is called a homomorphism from (S,*) to (S’,*) if

f(a*b)=f(a)*’f(b) for all a, b in S

Q1. If f is homomorphism from a commutative semi- group (S,*) onto a semi group (S’,*) then (S’,*’)s also commutative.

Sol: Let s1 and s2= f(s1)*’f(s2)=f(s1* s2)

=f(s2)*’f(s1)

=s2’*s1’

(S’,*’) is also commutative

4.6 Congruence Relation:

If m is ny positive integer and if a, b are any integrs then a is said to be congruent to b modulo m if m divides (a-b)(i.e if (a-b/m) has zero remainder.

Q1. Find a set of three real numbers that is closed under addition modulo 2 and multiplication modulo 2.

Soln: Consider the set (-1,0,1) and prepare the two tables addition modulo 2 and multiplication modulo 2.

• 4.6a Residue classes: Since congruence is an equivalence relation, it partion Z, the set of integers into disjoint equivalence classes called the residue classes modulo m.The residue class of a is the set of integers which are congruent to a modulo m.
• 4.6b Congruence relation on semi group: An equivalence relation R on the semi group (S,*) is called a congruence relation on semi group if a R a’ and b R b’ then (a*b) R (a’*b’)
• 4.6c Cyclic Group: A group (G,*) is said to be a cyclic group if there exists an element ae g such that every element of G can be written as som power of a viz. ak for some integer k where by ak we mean a x a x a…..a(k times)

Then G is said to be generator by a.

4.6d Subgroup: Let H be a subset of grou, such that

I) the identity element e of g belog to H.

Ii) if a, b belongs to H then a * b also belongs to H.

Iii)  if a € H then a-1 € H. Then H is called a subgroup of G.

• 4.6e Coset : For a subgroup 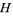 of a group  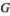and an element  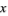of 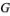, define  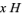to be the set  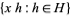and 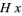 to be the set 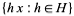. A subset of  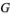of the form  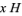for some  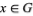is said to be a left coset of  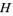and a subset of the form  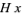is said to be a right coset of.
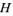• 4.6f Normal subgroup: A subgroup H of G is said to be normal if for every a € G we have aH=H. A subgroup of an Abelian group is normal.
• 4.6g Product Group: if G1 and G2 are groups and G=G1 X G2 then G is called a product group under the operation defined by

(u,v)*(x,y)=(u*x, v*y)

4.7 Partially Ordered Set (POSET)

A partially ordered set consists of a set with a binary relation which is reflexive, antisymmetric and transitive. "Partially ordered set" is abbreviated as POSET.

Examples

The set of real numbers under binary operation less than or equal to (≤)(≤) is a poset.

Let the set S={1,2,3}S={1,2,3} and the operation is ≤≤

Be {(1,1),(2,2),(3,3),(1,2),(1,3),(2,3)}{(1,1),(2,2),(3,3),(1,2),(1,3),(2,3)}

This relation R is reflexive as {(1,1),(2,2),(3,3)}∈R{(1,1),(2,2),(3,3)}∈R

This relation R is anti-symmetric, as

{(1,2),(1,3),(2,3)}∈R and {(1,2),(1,3),(2,3)}∉R{(1,2),(1,3),(2,3)}∈R and {(1,2),(1,3),(2,3)}∉R

This relation R is also transitive as {(1,2),(2,3),(1,3)}∈R{(1,2),(2,3),(1,3)}∈R.

Hence, it is a poset.

4.8 Coding

A word is a sequence of letters carrying some meaning. Suppose we decide to send a message in terms of 0 and 1 by using code.

Then the word ‘cad’ can be written as “100011”.

Encoding Function: if an integers n>m and if there is one to one correspondence e : Bm Bn then e is called an (m,n) encoding function . In this way every word in Bm is represented b y a words in Bn.

4.9 Group codes:-

An (m, n) coding function

E: BmBn  is called a group code if

E(Bm) = {e(b)/ b EBM}

= Range (e)

Q.1) Show that (2, 5) encoding function e B2 B5 defined by

e(00) = 00000    e(10) = 10101

e (01) = 01110    e(11) = 11011

Is a group code.

Let N = {00000, 01110, 10101, 11011}

We have that N is a sub group of B5

We shall prepare table for B5

0 + 0 = 0  0 + 1 = 1  1 + 0 = 0  1 + 1 = 0

Eg. 11011+01110=10101.

From the diagonal element true see that identity (00000) of B5 is N.

x, y belong to N then n + y also belong to N

Every element is it inverse.

It a group code.

Example 3: Consider the following (3, 8) encoding function e: B3   B8 defined by

How many errors can e detect?     

Sol: There will be 8C2 = 28 pairs of code words. The minimum distance is 3. By the above theorem if minimum distance is k + 1 = 3, then the coding function can detect 2 = k or less errors.

Example 4: Show that (3, 7) encoding function e defined below is a group code.

e(000)=0000000  e(001)=0010110  e(010)=0101000

e(011)=0111110  e(100)=1000101  e(101)=1010011

e(110)=1101101  e(111)=1111011

How many errors can it detect?

Sol.:

From the diagonal elements of the above table we see that (0000000) is an identity and it belongs to N.

From the table we also see that if x, y belong to N then x  y belongs to N.

Every element is its inverse.

N is a subgroup of B7 and the given encoding function is a group code.

The minimum distance is 2. Hence, the code can detect 1 or less errors.

Question bank

Prove that set A (0,1,2,3,4,5) is a finite abelian group under addition modulo 6.

Let S =(a,b,c,d) and R=(p,q,r,s)  consider fllwing operation.

Let f(a)= p , f(b)=q, f(c)=r , f(d)=s. Show that f is isomorphism.

Let g be set of all nn zero real numbers and let a*b= ab\2. Show that (G,*) is an abelian  group.

Show that (2, 5) encoding function e B2 B5 defined by

e(00) = 00000    e(10) = 10101

e (01) = 01110    e(11) = 11011

Is a group code.

Find the minium distance f (2,4) encoding function

E(00)=0000

E(10)=0110

E(01)=1011

E(11)=1100

4.10 Ring

The algebraic structure (R, +, .) which consisting of a non-empty set R along with two binary operations like addition(+) and multiplication(.) then it is called a ring.

An algebraic ( or mathematically) system (R, *, o) consisting of a non-empty set R any two binary operations * and o defined on R such that:

(R, *) is an abelian group and (R, 0) is a semigroup.

The operation o is the distributive over the operation * is said to be the ring.

4.11 Types of Rings

1. Null Ring

The singleton (0) with binary operation + and defined by 0 + 0 = 0 and 0.0 = 0 is a ring called the zero ring or null ring.

2. Commutative Ring

If the multiplication in a ring is also commutative then the ring is known as commutative ring i.e. the ring (R, +, .) is a commutative ring provided.

a.b = b.a for all a, b E R

If the multiplication is not commutative it is called non- commutative ring.

3. Ring with unity

If e be an element of a ring R such that e.a = a.e = a for all E R then the ring is called ring with unity and the elements e is said to be units elements or unity or identity of R.

4. Ring with zero divisor

A ring (R, +, .) is a said to have divisor of zero (or zero divisor), if there exist two non-zero elements a, b E R such that a.b = 0 or b.a = 0 where 0 is the additive identity in R . Here a and b are called the proper divisor of zero.

5. Ring without zero divisor

A ring R is said to be without zero divisor. If the product of no two non zero elements of R is zero i.e. if ab = 0 => a = 0 or b = 0.

4.12 Ring homomorphisms and isomorphisms

A map f : R→ S between rings is called a ring homomorphism if
f(x + y) = f(x) + f(y) and f(xy) + f(x)f(y) for all x, y ∈ R.

A ring homomorphism which is a bijection (one-one and onto) is called a ring isomorphism.

If f : R → S is such an isomorphism, we call the rings R and S isomorphic and write R 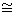 S.

Eg.

The map from Z to Zn given by x ↦ x mod n is a ring homomorphism. It is not (of course) a ring isomorphism.

The map from Z to Z given by x ↦ 2x is a group homomorphism on the additive groups but is not a ring homomorphism.

The map from Z to the ring of 2 × 2 real matrices given by x ↦ 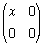 is a ring homomorphism which does not map the multiplicative identity to the multiplicative identity.

Of course the map x ↦ x mod n is a homomorphism which does map the identity to the identity.

The "evaluation at 1/2 map" from the ring of continuous real-valued functions on the interval [0, 1] to R given by (e½)f = f (1/2) for f belongs C[0, 1] is a ring homomorphism.

The "evaluation at 1 map" from the ring Q[x] to Q given by (e1)p = p(1) for p ∈ Q[x] is a ring homomorphism.
That is: e1(a0 + a1x + a2x2 + ... + anxn) = a0 + a1 + a2 + ... + an.

The "evaluation at √2 map" from Z[x] to R given by p ↦ p(√2) is a ring homomorphism.
This will turn out to be a surprisingly important example.

The map from C to ring of 2 × 2 real matrices given by a + bi ↦ 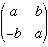 is a ring isomorphism.

4.13 Kernel of ring

The kernel of a (ring) homomorphism is the set of elements mapped to 0.

That is, if f: R→ S is a ring homomorphism, ker(f) = f-1(0) = {r ∈ R | f(r) = 0S }.

Theorem

The kernel of a ring homomorphism is an ideal.

Ideas of ring polynomial

R is a ring, the ring of polynomials in x with coefficients in R is denoted  . It consists of all formal sums

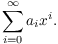
Here 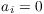 for all but finitely many values of i.

4.14 Principle of Duality:

The dual of any expression E is obtained by interchanging the operation + and * and also interchanging the corresponding identity elements 0 and 1, in original expression E.

Truth Tables for the Laws of Boolean

Boolean Expression	Description	Equivalent Switching Circuit	Boolean Algebra Law or Rule
A + 1 = 1	A in parallel with 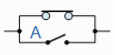closed = “CLOSED”		Annulment
A + 0 = A	A in parallel with 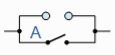open = “A”		Identity
A . 1 = A	A in series with 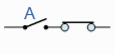closed = “A”		Identity
A . 0 = 0	A in series with 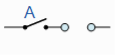open = “OPEN”		Annulment
A + A = A	A in parallel with 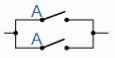A = “A”		Idempotent
A . A = A	A in series with 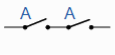A = “A”		Idempotent
NOT A = A	NOT NOT A (double negative) = “A”		Double Negation
A + A = 1	A in parallel with 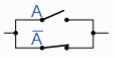NOT A = “CLOSED”		Complement
A . A = 0	A in series with 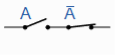NOT A = “OPEN”		Complement
A+B = B+A	A in parallel with B = 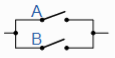B in parallel with A		Commutative
A.B = B.A	A in series with B = 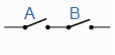B in series with A		Commutative
A+B = A.B	Invert and replace OR with AND		De Morgan’s Theorem
A.B = A+B	Invert and replace AND with OR		De Morgan’s Theorem