MODULE 5

Graphs And Trees

5.1 Graphs :-

Ordered par of finite non – empty sets and

* Vertices:- Element of V are called vertices. It is also called as node.

* Edge:- Element of E are called edges.

* Loop:- If an edge starts & end in same mertex then its called a loop.

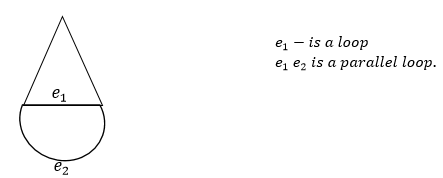
*Simple graph:- A graph having no loops or parallel edge.

* Adjacent vertices:-

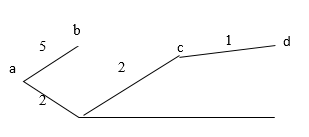
* Incident edge:- If edge from vertex

Eg. :- 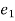starts from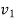 

* Degree of vertex:- The number of edge from that vertex

* eg.: 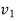 degree is 2

degree is 2.

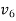degree is 1.

Note:

*  The sum of degree of all vertices of any graph is equal to twice number of edge.

* Determine the number of edges in a graphs with 6 nodes, 2 of degree 4 and 4 of degree 2. Draw two such graphs.

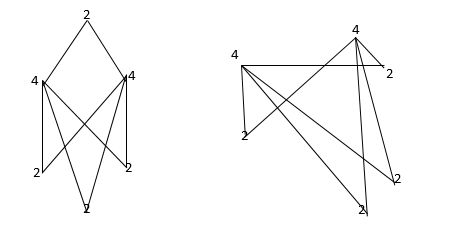
Note: The total number of edges is n(n – 1) /2 where n is number  off vertices.

Q.  Verify the result that the number of edge = n (n – 1) /2 for graph.

Now there are 10 edges.

1. 4 edges (), j = 2, 3, 4, 5
2. 3 edges (), j = 3, 4, 5
3. 2 edges (), j = 4, 5
4. 1 edge ()

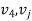Since there are 5 vertices m = 5

No. Of edges    =

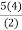= 10 as shown

5.2 Bipartite graph: -

A graph G = (V, E) is called bipartite if its satisfies full condition

i.  V can be expressed as an union of two disjoint sets  U &  W.

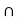[ i.e. U W= V & U W=]

Ii. Every edge in E has one vertex in U and other in W.

Q.  Show that the graph is a bipartite.

Let  V =

U =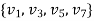

W =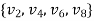

Every edges has one nitrox in W. Hence it is dipartite graph. 

5.3 Isomorphism: -

Two graphs are said to be isomorphic if there exist one to one correspondence from I to V.

1. They must have same no. Of vertices.

2. They must have same no. Of edges.

3. They must have same degree of vertices.

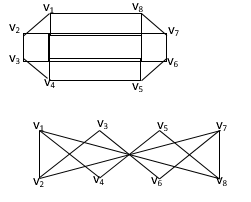
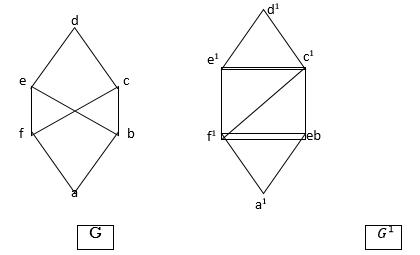
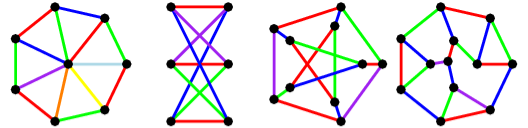
Q.  Are the following pairs of graphs isomers?

Yes, & both have 4 vertices, 5 edges

2 vertices of degree 2.

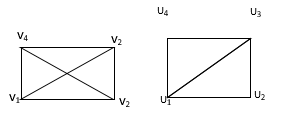
2 vertices of degree 3.

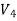
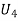
Q. Determine whether are isomorphic   

i)  The same no. Of vertices viz. 6

Ii) But they do not have same number of edges, G has 8  edges, “G” has 7 edges.

Iii) In “G” the vertex “C” is of degree 44.

In G there is no vertex of degree 4.

G & 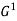are not isomorphic.

5.4 Graph Colouring

Graph colouring problem is to assign colours to certain elements of a graph subject to certain constraints.

Vertex colouring is the most common graph colouring problem. The problem is, given m colours, find a way of colouring the vertices of a graph such that no two adjacent vertices are coloured using same colour.

The other graph colouring problems like Edge Colouring (No vertex is incident to two edges of same colour) and Face Colouring (Geographical Map Colouring) can be transformed into vertex colouring.

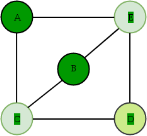
Chromatic Number: The smallest number of colours needed to colour a graph G is called its chromatic number. For example, the following can be coloured minimum 3 colours.

5.5 Colouring a Cycle Graph

Cycle:- cycle is a path of edges and vertices wherein a vertex is reachable from itself. Or in other words, it is a Closed walk.
 

Even Cycle: - In which Even number of vertices is present is known as Even Cycle.
 

Odd Cycle: - In which Odd number of Vertices is present is known as Odd Cycle.

Given the number of vertices in a Cyclic Graph. The task is to determine the Number of colours required to colour the graph so that No two Adjacent vertices have the same colour.

Example 1: Even Cycle: Number of vertices = 4
 

Colour required = 2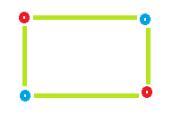
 

Example 2: Odd Cycle: Number of vertices = 5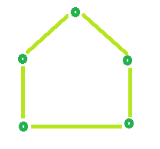
 

Color required = 3
 

Planarity – “A graph is said to be planar if it can be drawn on a plane without any edges crossing. Such a drawing is called a planar representation of the graph.”

Important Note – A graph may be planar even if it is drawn with crossings, because it may be possible to draw it in a different way without crossings.
For example consider the complete graph  and its two possible planar representations –
 

Theorem – “Let G be a connected simple planar graph with e edges and V vertices. Then the number of regions R in the graph is equal to  e- v- (K+1)
where k is the no. Of component in the graph..”

• Example – What is the number of regions in a connected planar simple graph with 20 vertices each with a degree of 3?
• Solution – Sum of degrees of edges = 20 * 3 = 60. By handshaking theorem, 2e=60  which gives  e= 30.
  By Euler’s theorem, the number of regions =  e-v +2  which gives 12 regions.

5.6 Edge Coloring

An edge colouring of a graph  is a colouring of the edges of  such that adjacent edges (or the edges bounding different regions) receive different colours. An edge colouring containing the smallest possible number of colours for a given graph is known as a minimum edge colouring.

A (not necessarily minimum) edge coloring of a graph can be computed using Edge Coloring[g] in the Wolfram Language package Combinatoric .

The edge chromatic number gives the minimum number of colors with which graph's edges can be colored

5.7 Trial, Paths and circuit representation

        A trial from v to w is a walk from v to w that does not contain a repeated edge.

        A path from v to w is a trial that does not contain a repeated vertex.

        A closed walk is a walk that starts and ends at the same vertex.

Q. In the graph below, determine which of the following walks are trails, paths, circuits 02 simple circuits.

1. v1 e1 v2 e3 v3 e4 v3 e5 v4   b. e1 e3 e5 e5 e6

c.      v2 v3 v4 v5 v6 v2   d. v2 v3 v4 v5 v6 v2

e.     v1 e1 v2 v1

Soln:

1. This walk has repeated vertex, but does not have a repeated edge, so it is a trial from v1 to v4 but a path.
2. This is just a walk from v1 to v5 it is not a trail because it has a repeated edge.
3. This walk starts and ends at v2 contain at least one edge and does not have a repeated edge, so it is a circuit. Since the vertex v3 is
4. This walk starts and ends at v2, contains at least one edge, does not have a repeated edge, and does not have a repeated vertex. Thus, it is a simple circuit.
5. This is just a closed walk starting and ending at v1. It is not a circuit because edge e1 is repeated.
6. The first vertex of this walk is the same as its last vertex, but it does not contain an edge, and so it is not a circuit. It is a closed walk from v1 to v1. (It is also a trail from v1 to v1)

        Trees and Rooted trees

A graph is said to be circuit free if and only if it has no circuit. A graph is called a tree if & only if it is circuit free & connected.

A graph is called a forest if and only if it is circuit free and not connected.

        Terminal Vertex: Let T be tree. If T has only one or two vertices.

Theorem 1: For any positive integer , any three with n vertices has n – 1 edges.

5.8 Rooted Trees:

A rooted tree is a tree in which there is one vertex that is distinguished from others is called the roots.

5.9 Spanning Tree:-

Let G be a simple graph A spanning tree of G is a sub graph of G that is a tree containing every vertex of G.

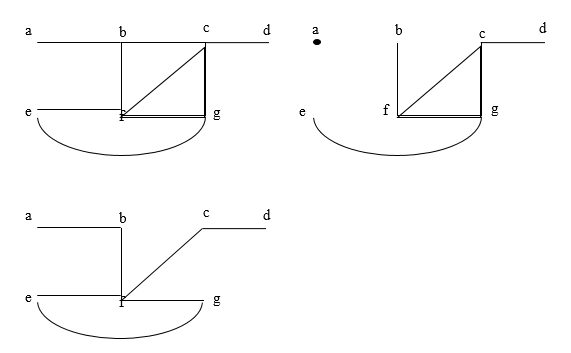
Q. Find the spanning tree

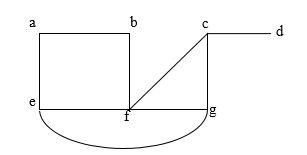
It is not a tree, because it contains simple circuit.

1. Remove edge {a, e}. This eliminates one ckt. And subgraph is connected to vertex G.
2. Now remove edge {e, f} to eliminate a second simple circuit.
3. Finally remove edge {c, g} to produce a simple graph with no simple ckt.

This subgraph is spanning tree, because it is a tree that contain vertex of G

5.10 Weighted graph:

A graph G is said to be weighted graph if all the edge of a graph G is assigned a non-negative real number.

        Weighted tree

A tree T is said to be a weighted Tree is all the edges of a T is assigned a non – negative real number.

        Minimum spanning tree

A minimum spanning tree is a connected weighted graph is a spanning tree that has the smallest possible sum of it edges.

5.11 Prism Algorithm

Prism Algorithm to find minimum spanning tree of a weighted graph.

Input G – weighted connected undirected graph with n vertices.

T = a minimum weight edge for i = 1 to n – 2.

e = an edge of min weight incident to a vertex in T.

t = T with e added return T.

5.12 Kruskal’s Algorithm

Kruskal’s Algorithm to find minimum spanning Tree of weighted graph.

Input G:- Weight connected undirected graph with a vertices.

T = empty graph .     [i = 1 to n – 1]

e ≠ any edge in G with smallest weight that does not form a simple circuit

T = T with e added return T.

Q. Show the steps in execution of Dijkstras shortest path algorithm for graph.

Solution : - Step 1: - Going into while loop.

V(T) = (a), E (T) = ø and f = {a}

During iteration :-

F = {b, c}   L(b) = 3  L(c) = 4

Since L(b) < L(c), b is added to V(T) and {a, b} is  added to E(T).

Step 2 Going into while loop: V(T) = {a, b}

E(T) = {(a, b)}

F = {c, d, e}

L(c) = 4  L(d) = 9  L(e) = 8

Since L(c) < L(d) and L(c) < L(e)

c is added to V(T) and {a, c} is added to E(T).

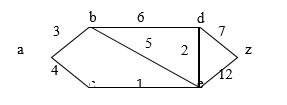
Step 3:- Going into while loop V(T) = {a, b, c} E(T) = {(a, b), (a, c)}

During iteration

F = {d, e}   L{d} = 9   L(e) = 5

Since L(e) < L (d)

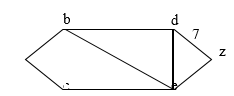
Step 4:- Going into while loop V(T) = {a, b, c, e}

E(T) = {(a, b), (a, c), (c, e)}

During iteration

F= {d, z}  L(d) = 7  L(z) = 17

L(d) becomes 7 because aced, which has length 7 is a shorter path.

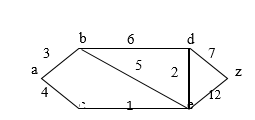
Step  5:- Going into while loop V(T) = {a, b, c, e}

During iteration: -

E(T) = {(a, b) (a, c) (c, e)}

F = {z},  L (z) = 14 L(z) become 14 because a c e d z, which has length 14 is a shorter path to d than a b d z.

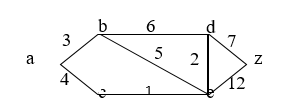
Q. Apply Dijkastra’s Algorithm to find  the  shortest path from vertex “a” to all the remaining vertices of a graph below.

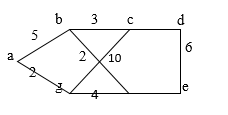
1. Initially λ(a) = 0

λ(b) = min { λ (b), 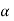(a) + w(a, b) }

= min {∞, 0 + 5} = 5

λ(9) = min { λ(g), λ(a) + w (a, g)}

= min {∞, 0 + 2} = 2

Vertices adjacent to g are c f

λ(c) = min { λ (c), λ (g) + w(g, c)}

= min {∞, 2 + 2} = 4

λ(f) = min {∞, 2 + 4} = 6

Vertices adjacent to c are b, d

λ(b) = min { λ (b), λ (c) + w(c, b)}

= min {5, 4 + 3} = 5

λ(d) = min { λ(d), λ(c) + w (c, d)}

= min {∞, 4 + 1} = 5

Vertex adjacent to d is e

λ(e) = min { λ (e), λ(d) + w(d, e)}

= min {∞, 5 + 6} = 11

Vertex adjacent to b is f

λ(f) = min { λ (f), g (λ (b) + w(b, f)}

= min {6, 5 + 10} = 6